基于资源三号卫星的GPS/星敏感器组合导航方法研究
张 黎,陈梓昂,王 博
(南京航空航天大学 航天学院,南京 210016)
目前,以GPS、北斗为主的卫星导航技术体系,形成全方位、动态的全球立体导航定位服务,能够快速获取地面、海洋、空中目标物的精确位置,为精确制导武器、航天侦察与现代化地理信息服务提供强有力的技术支撑[1]。然而,定位服务不仅仅要求获取目标物的单点地理位置,同时还需要尽可能地确定目标物的空中姿态。通常,定位和定姿被视为两个独立的过程,在组合导航过程中其相关性也经常被忽略[2-4]。当前应用最为广泛的组合导航是卫星导航系统和惯性导航系统的组合,其确定空中目标物姿态的通常做法是在目标物上装载惯性测量设备和系统,例如陀螺仪、角速度计等,用于量测目标物在连续时间内的角速度,计算目标物的瞬时姿态[5]。这种做法存在两个方面的问题:一是随着时间的累计,惯性测量设备量测误差会累积起来,导致目标物飞行距离越长,或目标物定位服务时间越长,其瞬时姿态的计算精度越低,长距离或长时间导航会受到严重限制;二是惯性测量设备制造与维护的费用较高,量测精度越高,成本越高,对于大规模的行动来说性价比较低。
研究多层次、多平台的定位定姿新模型、新方法与新技术,对于增强空中目标物实时量测与控制能力,降低设备制造与维护的成本费用具有重要意义。星敏感器作为一种高精度的姿态测量仪器, 越来越广泛地应用于各种空间飞行器中, 具有体积小、功耗低、精度高且测量误差不随时间积累等显著优点[6]。文中基于资源三号卫星数据,提出一种GPS/星敏感器组合导航定位定姿方法,针对GPS定位以及星敏感器定姿的误差问题,对两类过程中的误差使用卡尔曼滤波进行综合处理,提高长距离或长时间目标导航追踪能力。
1 GPS/星敏感器组合导航方法
1.1 GPS姿态求解
进行组合导航时,采用卡尔曼滤波需输入GPS与星敏感器输出的姿态角分量之差,因此需要首先根据位置等信息计算GPS姿态。确定GPS姿态的方法有直接法、矢量观测法、最小二乘法等[7-9]。直接法在计算载体姿态时需要用到载体坐标系和当地水平坐标系,利用直接法计算姿态角仅需当前历元的两个不相关基线矢量,计算较为简单。
在GPS姿态测量中会使用到载体坐标系,载体坐标系是用户根据自己所用的载体平台所定义的坐标系,通常把它的原点取为载体质心,X轴沿载体运动方向,Y轴垂直X轴指向载体右侧,Z轴垂直载体向上。载体坐标系是靠载体上GPS天线的位置确定,如图1所示。
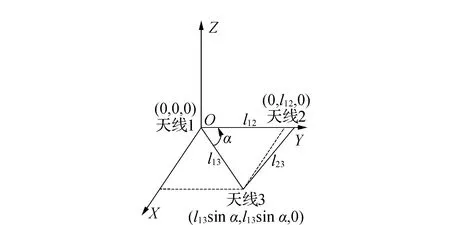
图1 载体坐标系示意图
利用坐标转换矩阵,能将参考坐标系中的向量转换为载体坐标[10]。
(1)
其中,bl=(xl,yl,zl)T表示基线在当地水平坐标系中的向量,bb=(xb,yb,zb)T表示基线在载体坐标系中的向量,可以通过一定算法求出3个姿态角的值φ,θ和ψ。若GPS天线的载体坐标系设置如图1所示,且天线2和天线3在当地水平坐标系中的坐标分别为ul2=(xl2,yl2,zl2)T和ul3=(xl3,yl3,zl3)T,可得到式(2)从而计算出3个姿态角的值。
(2)
基线矢量在载体坐标系中的坐标可以事先设定,并且由于基线矢量与载体固连在一起,所以基线矢量在载体坐标系中的坐标是一直不变的。假定其中一个基线是沿载体运动方向安装的,设基线向量在载体坐标系中的坐标为Xb=(b, 0, 0),b为基线长度,假定基线在当地水平坐标系中的坐标已通过计算得出为Xl2=(xl2,yl2,zl2)。根据式(1),又姿态矩阵是正交的,可求得偏航角φ和俯仰角θ[11]。
(3)
(4)
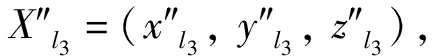
(5)
1.2 组合导航方案
卡尔曼滤波作为一种降低、分离卫星信号中所含有噪声量的技术,是消除导航定位定姿随机误差的重要方法,在提高精度方面具有重要作用。进行组合导航时,卡尔曼滤波应该具有相同的输出分量,GPS系统输出为位置、速度及解算得到的姿态,星敏感器输出为姿态。本方案针对有惯导系统的组合导航,所消除的误差有陀螺的常值漂移和加速度计的零偏,而可能产生的误差为星敏感器低频误差[12-14]。
本方案以姿态运动学方程构建姿态与角速度、角加速度的关系——系统状态方程,以GPS接收机与星敏感器输出的姿态角分量之差为观测方程,将恒星影像成像时刻的欧拉姿态角等作为多余观测分量,将星敏感器成像过程中的低频误差作为状态估计量,从而得到当前最优姿态欧拉姿态角、GPS位置以及速度,并实时更新下一时刻的系统增益和协方差矩阵。
建立状态方程[15]:XS(k+1)=FXS(k)+v(k),其中,F为状态转换矩阵,XS为状态向量矩阵,v为系统噪声。
拟建立观测方程:ZG(k)=HXS(k)+w(k),其中,ZG为观测向量矩阵,H为观测矩阵,w为观测噪声。
根据卡尔曼滤波增益K可以动态调整状态量与观测量的权值,从式(6)中可以看出,卡尔曼增益可以通过给出的协方差矩阵初值P0不断迭代更新,从状态估计方程式(7)中可以看出,K越小时状态估计的权值将越大,K越大时观测值的权值将越大。
滤波增益方程为:
K(k)=P(k|k-1)HT[HP(k|k-
1)HT+W]-1.
(6)
状态估计方程为:
(7)
误差协方差矩阵为:
P(k)=[I-K(k)H]P(k|k-1)[I-
K(k)H]T+K(k)WK(k)T.
(8)
(9)
状态方程可以写为:
(10)
状态转换矩阵可以由式(11)获得。
(11)
由于欧拉角可以直接测量获取,所以测量敏感矩阵可以简化为:
H=[1,0,0]T.
(12)
由于只有单个姿态被估计,所以测量噪声协方差矩阵是一个标量。另外过程噪声协方差矩阵算式为:
(13)
系统误差协方差矩阵的初值可由式(14)计算。
(14)
根据给定初值,按照图2给出的算法执行流程,即可进行卡尔曼滤波。

图2 GPS/星敏感器卡尔曼滤波组合导航流程
2 实验与分析
选取资源三号卫星在2019年1月21日4时至4时20分的数据,使用其中的GPS定位数据和星敏感器姿态数据(星上下传数据为四元数,实验中转换为欧拉角)。采样间隔为10 s,设置GPS测量噪声均方差为1 m,星敏感器测量噪声均方差为20″,原始轨迹与输出的滤波轨迹分别如图3、图4所示,输出的滤波结果如图5所示,各参数估计偏差最大值(max)和估计偏差均方根(RMS)比较如表1所示。

表1 估计偏差最大值(Max)和估计偏差均方根(RMS)

图3 原始轨迹

图4 滤波轨迹

(a)位置误差 (b)姿态角误差
可以看出,随着时间变化,通过卡尔曼滤波修正得到的位置姿态误差趋于平稳收敛,滤波器估计性能较好,各参数估计偏差曲线稳定,估计精度与采用惯性系统的组合导航方式精度相当,并且能够避免惯性系统误差随时间累积的固有缺陷。实验结果表明,该GPS/星敏感器组合导航方案能够实现修正定位定姿误差的要求。
将GPS测量噪声均方差设置为10 m,输出的滤波轨迹如图6所示,输出的滤波结果如图7所示,各参数估计偏差最大值(Max)和估计偏差均方根(RMS)比较如表2所示。

图6 噪声增加后滤波轨迹

图7 噪声增加后滤波结果
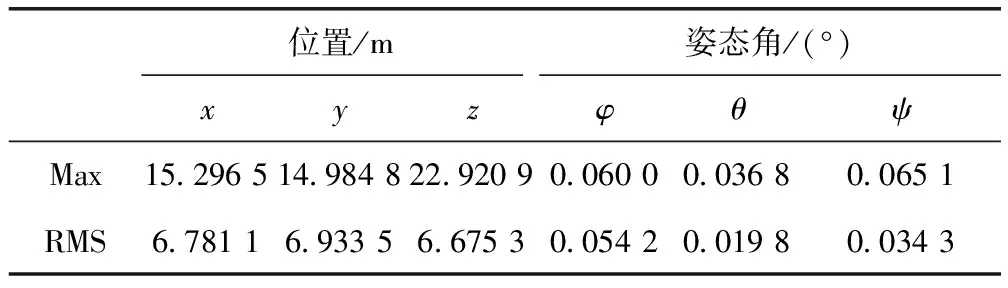
表2 噪声增加后估计偏差最大值(Max)和估计偏差均方根(RMS)
可以看出,当GPS测量噪声均方差增加为10 m时,该组合导航方案滤波性能总体维持较好水平,对比噪声均方差为1 m时,对位置误差的修正性能略有下降,对姿态角误差的修正性能依然可观,3个姿态角中,俯仰角误差均方根仍维持在0.02°以下,其原因在于组合导航滤波时动态调整了状态量与观测量的权值,当GPS噪声增加时,状态估计(即星敏感器输出)的权值增加,从而获得了较好的姿态修正效果,表明星敏感器作为一种高精度的姿态测量仪器,能够在与GPS组合导航中获得较好的姿态确定和修正效果。总的来说,该组合导航方案在GPS精度较高时滤波性能更优。
3 结 论
文中基于资源三号卫星数据,对于其中的GPS定位数据和星敏感器姿态数据,提出一种基于GPS/星敏感器组合导航定位定姿方法,将GPS姿态测量应用于组合导航场景,拓展其在组合导航方向上的研究前景。通过实验分析表明该方案具有一定可行性和优越性,其估计精度与采用惯性系统的组合导航方式精度相当,并且能够避免惯性系统误差随时间累积的固有缺陷,有效抑制GPS位置误差和星敏感器低频误差,能够实现修正定位定姿误差的要求,提高长距离或长时间目标导航追踪能力。同时文中还存在一些有待进一步研究改进的地方,未来的研究方向为改进GPS姿态测量方法,使用矢量观测法和最小二乘法提高定姿精度。另外,对卡尔曼滤波器进行改进,提升滤波性能,对滤波的精度和稳定性进一步研究。

