基于预报星历和基准站辅助的BDS实时精密单点定位

范士杰，顾宇翔，胡锦民，陈 岩，舒国权

(1.中国石油大学(华东)海洋与空间信息学院，山东 青岛 266580；2马鞍山钢铁股份有限公司，安徽 马鞍山 243011)

GNSS精密单点定位是目前高精度卫星导航与定位的主要方法之一，具有单机定位、作业方式灵活、成本低等优势[1]，在水汽反演[2]、降雨预报[3-4]、卫星精密定轨[5-6]、地震监测[7]等领域应用广泛。基于中国北斗卫星导航系统的事后静态PPP精度可达cm级[8-9]。朱松等采用武汉大学提供的WUM事后精密轨道和钟差产品分析BDS动态PPP性能，发现收敛后可以获得优于10 cm的定位精度[10]；胡豪杰等利用CNES提供的BDS实时SSR改正信息对BDS实时PPP定位性能进行了分析，静态和动态模式下的平均水平定位精度分别优于10 cm和30 cm，而动态模式下的高程方向精度较差，其平均RMS为46 cm[11]。由于BDS的全球跟踪站有限，精密卫星轨道和钟差精度不如GPS，因此BDS PPP的收敛时间较长[12]，单BDS定位精度偏低且存在较多异常数据[11]。

黄观文、涂锐等提出的基于基准站改正信息的GPS PPP算法，通过基准站和流动站的共性误差改正，可消除与卫星有关误差影响，进而提高定位精度[13-14]。基于上述算法和WHU预报星历，利用香港卫星定位参考站网观测数据，开展了区域BDS实时PPP试验，对基准站辅助的BDS PPP算法及其定位性能进行分析和讨论。

1 基准站辅助的PPP算法

1.1 常规PPP的数学模型

利用双频接收机获取伪距和相位观测值，采用常规消电离层组合观测值作为PPP的数学模型，其观测方程为[15-17]：

(1)

(2)

式中:Pi和φi(i=1,2)分别为对应频率fi的伪距和载波相位观测值；PC和ΦC分别为消电离层组合伪距和相位观测值；ρ为站星距离；c为光速；dtr,dts分别为接收机和卫星钟差；dtrop为对流层延迟；Ni为载波相位观测值的整周模糊度；εP,εΦ为观测噪声。

利用IGS精密卫星钟差产品改正dts，将式(1)和式(2)线性化后得到：

L=AX+Bdtr+CN+dtrop+φm+φn+ε.

(3)

式中:L为无电离层组合伪距和载波相位观测值；X为坐标参数，AX为对应站星几何距离；dtr为接收机钟差参数；N为消电离层组合模糊度参数；B,C为系数；dtrop为对流层延迟改正；φm为模型化误差，包括卫星钟差、天线相位中心偏差、相对论效应、地球自转影响、固体潮、极潮、海潮改正等；φn为未模型化误差以及模型改正后的残余误差；ε为观测噪声。

利用上述观测模型，采用序贯最小二乘估计方法进行PPP计算。对流层干延迟采用Saastamoinen模型进行改正，湿延迟作为参数。参数估计时，位置参数X在静态处理时作为常未知数，动态处理时作为为动态参数；接收机钟差视为白噪声，作动态参数处理；模糊度参数在未发生周跳或周跳修复时为常数，发生周跳时作为一个新的常数参数进行处理；对流层湿延迟利用随机游走过程法估计[18]。

1.2 获取基准站改正信息

由式(3)可得基准站的观测方程：

L1=A1X1+B1dtr1+C1N1+

dtrop1+φm1+φn1+ε1.

(4)

基准站的坐标已知，因此可计算出站星几何距离A1X1。在基准站的观测方程中，减去站星几何距离和模型化误差，可得基准站改正信息：

ΔV=L1-A1X1-φm1=B1dtr1+

C1N1+dtrop1+φn1+ε1.

(5)

式中：ΔV包含了基准站接收机钟差、组合模糊度、对流层延迟、其他未模型化误差以及模型改正后的残余误差、观测噪声等。

1.3 基准站辅助的PPP

由式(3)可得流动站的观测方程：

L2=A2X2+B2dtr2+C2N2+dtrop2+

φm2+φn2+ε2.

(6)

将式(5)中的基准站改正信息附加到流动站，可得：

L2-ΔV=(A2X2+B2dtr2+C2N2+dtrop2+φm2+

φn2+ε2)-(B1dtr1+C1N1+dtrop1+φn1+ε1).

(7)

若提取流动站和基准站共视卫星的观测值构建观测方程，则其观测方程的系数矩阵相同，即B1=B2,C1=C2，则式(7)可合并为：

L2new=A2X2+B2(dtr2-dtr1)+C2(N2-N1)+

(dtrop2-dtrop1)+φm2+(φn2-φn1)+(ε2-ε1).

(8)

简化为：

L2new=A2X2+B2Δdt+C2ΔN+

Δdtrop+φm2+Δφn+Δε.

(9)

式中：Δdt,ΔN分别为流动站和基准站的接收机钟差、组合相位模糊度之间的差值，仍作为未知参数；流动站的对流层延迟误差得到一定程度的削减，当流动站距离基准站较近时，Δdtrop趋近于0；Δφn为流动站和基准站的未模型化误差及模型改正后的残余误差之间的差值；Δε为测量噪声。由于采用共视卫星的观测值构建观测方程，因此与卫星有关的轨道误差、卫星钟差等未模型化及模型改正后的残余误差被大大消弱，从而提高了流动站观测值的精度。

2 基于预报星历和基准站辅助的BDS实时精密单点定位

2.1 站点选取和试验方案

依托香港卫星定位参考站网，选取HKWS站为基准站，HKSL，HKNP，HKKT，HKSC，HKST等站点作为流动站。各流动站以基准站为中心大致呈散射状分布，流动站至基准站的距离如表1所示。

利用上述基准站和流动站在2018年第332～338 d连续一周的观测数据，基于WHU预报星历获取实时BDS卫星轨道和钟差改正，对各流动站开展BDS实时PPP试验。为了验证基准站改正信息对卫星轨道和钟差、卫星天线相位中心改正以及PPP定位精度的影响，文中设计了4种试验方案，对基准站辅助的BDS实时静/动态PPP算法及其定位性能进行分析和讨论。方案1：常规实时BDS PPP，不考虑卫星天线相位中心(PCO)改正；方案2：常规实时BDS PPP，考虑PCO改正；方案3：基准站辅助的实时BDS PPP，不考虑PCO改正；方案4：基准站辅助的实时BDS PPP，考虑PCO改正。其中，PCO改正采用IGS发布的BDS卫星天线相位中心改正模型[19-21]，见表2所示。

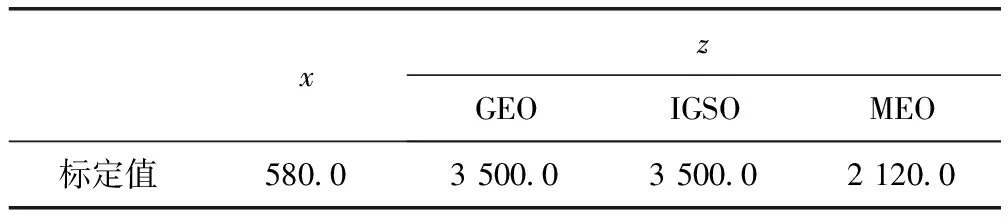
表2 IGS发布的BDS卫星天线PCO改正值 mm

2.2 结果分析

以IGS事后精密轨道和钟差产品解算的各流动站GPS静态相对定位周解坐标为参考值，对上述4种方案的BDS PPP结果进行比较和精度分析。

1)静态处理模式。对上述各流动站每天24 h的观测数据进行静态PPP解算，可获得其单天解坐标。以HKKT站为例，4种方案在N，E，U方向上的单天解坐标误差序列如图1所示。表3和表4分别给出了各流动站4种方案BDS静态PPP单天解坐标的误差统计(均方根误差RMS、标准差STD、平均偏差MEAN)和平均精度。

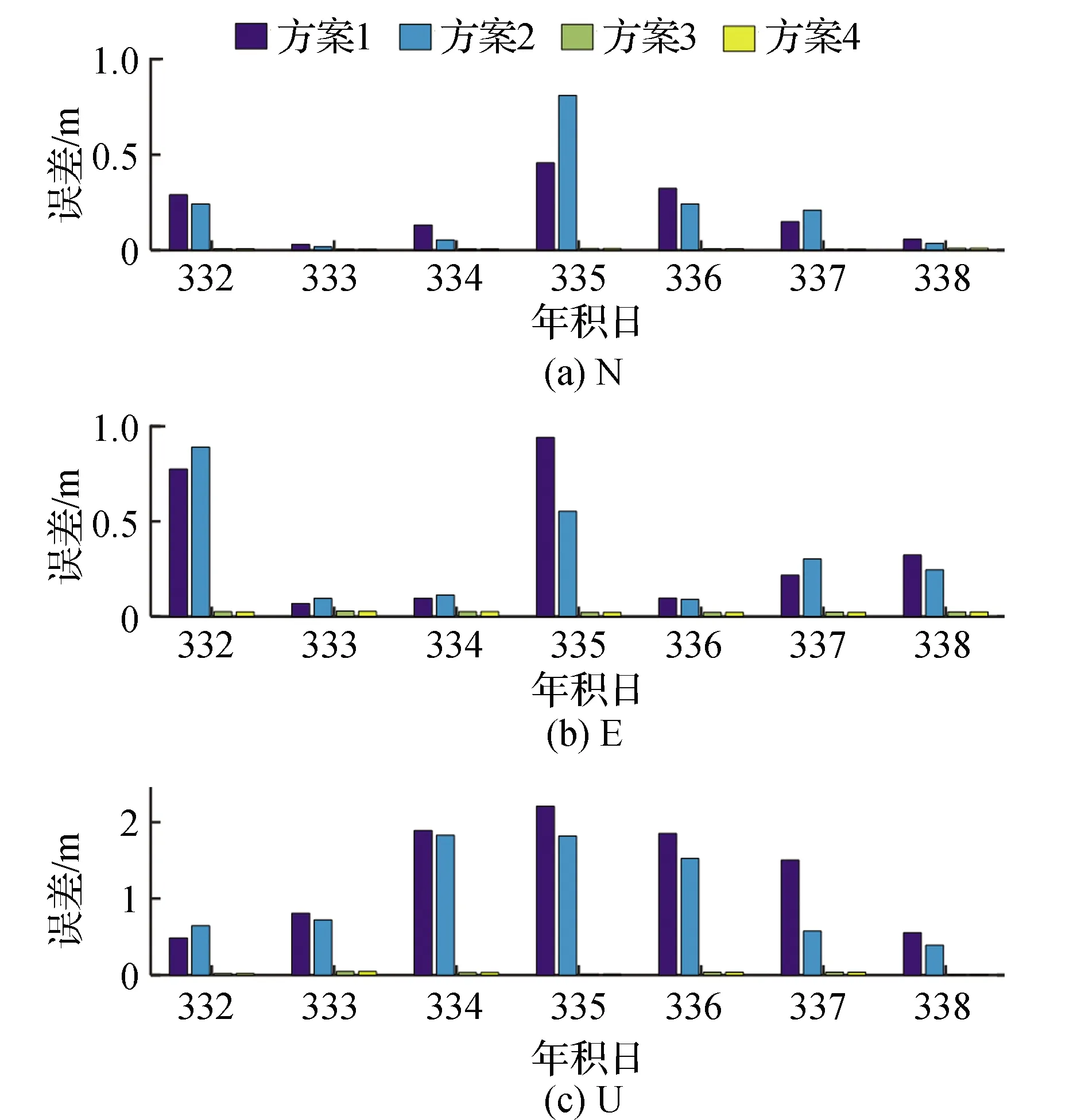
图1 HKKT站4种方案静态PPP单天解的坐标误差

均方根误差RMS的算式为：

(10)

其中，Δi在静态模式中为N,E,U方向上PPP单天解与参考值的差值，动态模式中为每一历元结果与参考值的差值；n在静态模式中为解算天数，动态模式中为历元数。

标准差STD的算式为：

(11)

平均偏差MEAN的算式为：

(12)

综合分析图1、表3和表4可以看出，方案3和方案4的定位误差明显小于方案1和方案2，基准站辅助的BDS PPP定位精度得到较大提升，其静态单天解的重复测量精度(STD)在水平方向优于1 cm，高程方向优于2 cm；相对于参考坐标，N,E,U方向的外符合精度(RMS)均优于5 cm；而常规BDS PPP的定位精度仅为dm级和m级。卫星天线相位中心改正对常规BDS PPP的影响主要为U方向，平均偏差和RMS均达到dm级，不可忽略；但是，卫星天线相位中心改正对基准站辅助的BDS PPP(方案3和方案4)没有影响，附加基准站改正信息可以消除流动站PPP中与卫星相关误差影响。

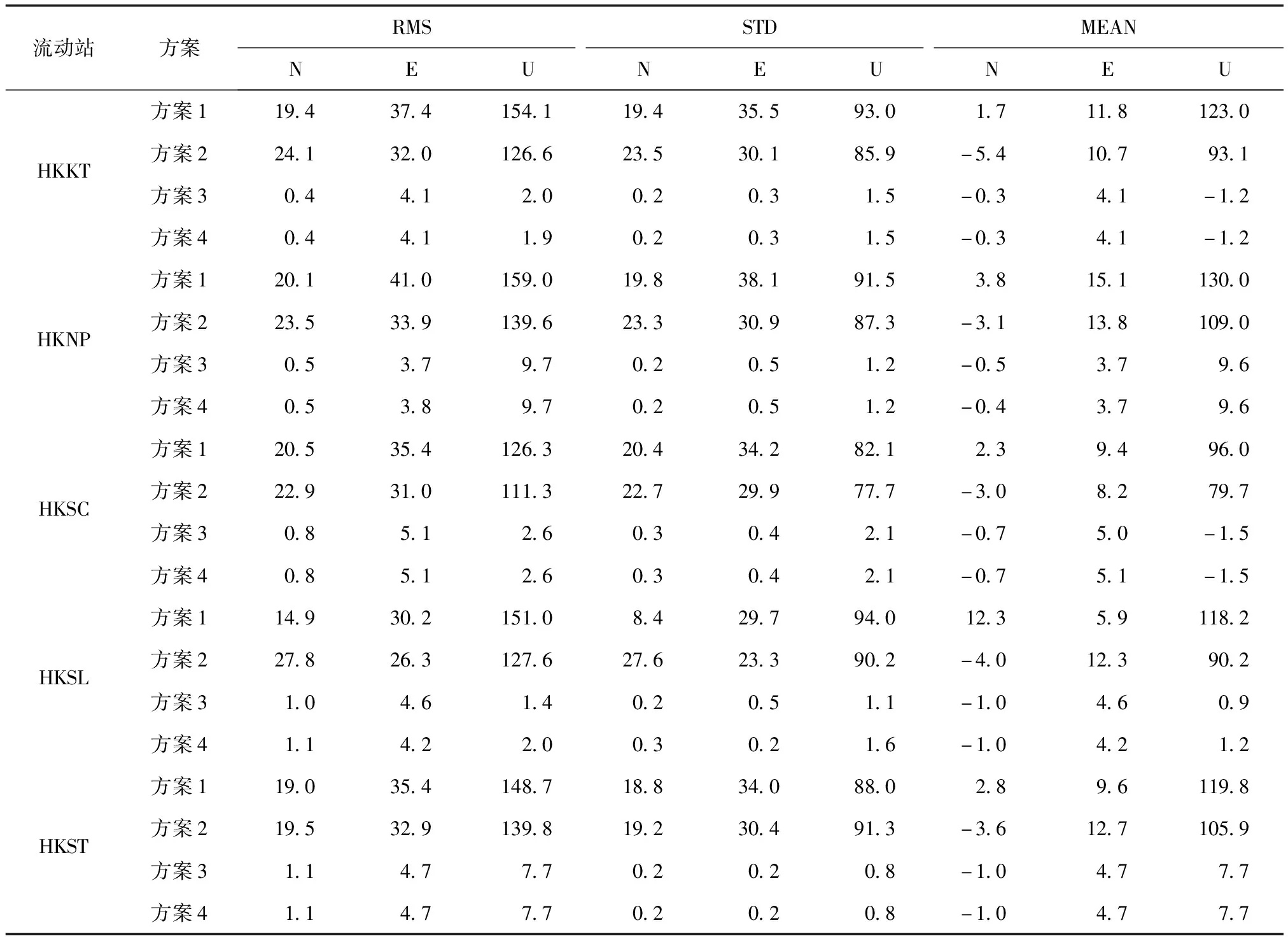
表3 4种方案静态PPP单天解坐标的误差统计 cm

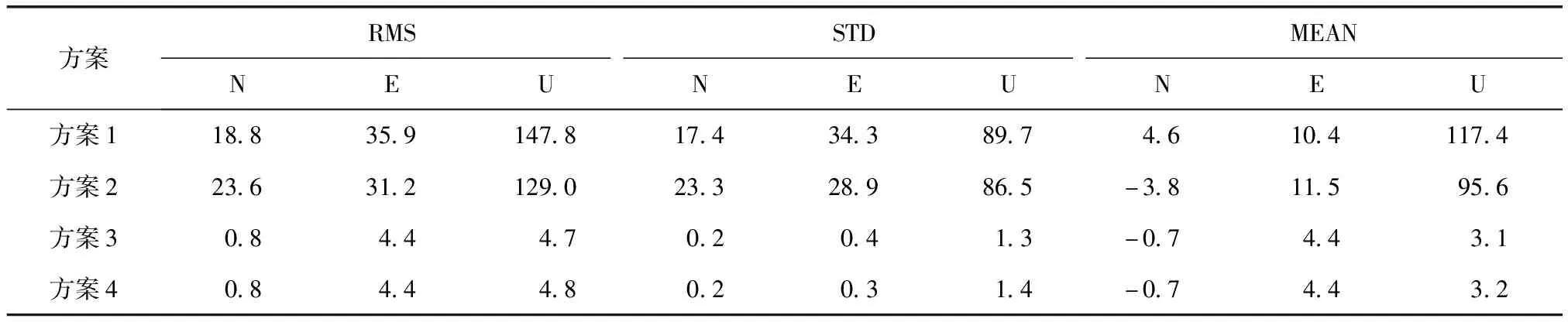
表4 4种方案静态PPP单天解坐标的平均精度 cm

2)动态处理模式。利用上述各流动站的BDS静态观测数据，进行模拟动态PPP解算。由于基准站辅助的BDS PPP算法可以消除PCO的影响，为更直观显示该算法对卫星轨道及钟差的改正效果，仅以方案2和方案3的动态处理结果为例进行比较。以HKSL站点第334 d为例，方案2和方案3在N,E,U方向上的BDS动态PPP误差序列如图2所示。表5和表6分别给出各流动站两种方案BDS动态PPP的误差统计和平均精度。

由图2和表5、表6可以看出，基于预报星历的常规BDS实时动态PPP(方案2)的相位模糊度难以收敛，其定位结果很不稳定，定位精度很差；而基于预报星历和基准站辅助的BDS实时动态PPP(方案3)的相位模糊度能够快速收敛(平均收敛时间约为102 min)，且收敛后的定位结果较为稳定，定位精度得到大幅提升，其重复测量精度(STD)在水平方向优于4 cm，高程方向优于10 cm；相对于参考坐标的外符合精度(RMS)在水平方向优于7 cm，高程方向优于15 cm。

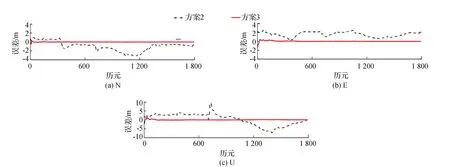
图2 HKSL站方案2和方案3的BDS动态PPP误差序列

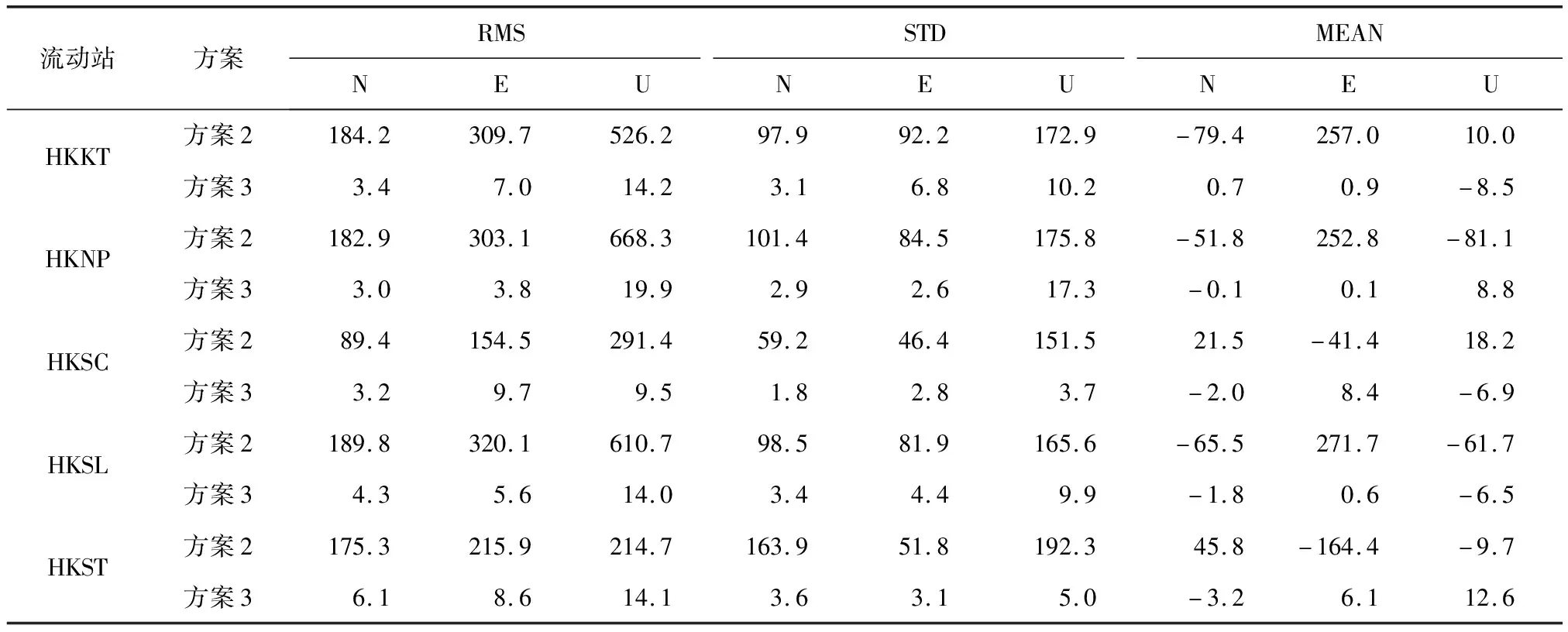
表5 方案2和方案3BDS动态PPP误差统计 cm

表6 方案2和方案3BDS动态PPP的平均精度 cm

3 结束语

利用香港卫星定位参考站网观测数据，开展基于预报星历和基准站辅助的区域BDS实时PPP试验，并以事后GPS PPP周解坐标为参考，对流动站BDS实时静态和动态PPP的定位性能进行分析，结论如下：

1)附加基准站改正信息，可以消除流动站和基准站共视卫星的轨道和钟差等影响，有效提升流动站BDS PPP的定位性能。基准站辅助的BDS实时静态PPP单天解重复测量精度(STD)在水平方向优于1 cm，高程方向优于2 cm；相对于参考坐标，N,E,U方向的外符合精度(RMS)均优于5 cm；基准站辅助的BDS实时动态PPP重复测量精度(STD)在水平方向优于4 cm，高程方向优于10 cm；相对于参考坐标的外符合精度(RMS)在水平方向优于7 cm，高程方向优于15 cm。

2)卫星天线相位中心(PCO)改正对常规BDS PPP的影响主要为U方向，平均偏差和RMS均达到dm级，不可忽略；但是，卫星天线PCO改正对基准站辅助的BDS PPP没有影响。基于预报星历和基准站辅助的BDS实时PPP具有算法稳定、高精度且易于实现等优点，在远海精密GNSS定位领域具有较好的应用价值。