等式约束病态总体最小二乘的修正奇异值解及精度评定
翁 烨,邵德盛,2
(1.昆明理工大学 国土资源与工程学院,昆明 650093;2.云南省地震局,昆明 650200)
病态问题广泛存在于自然科学和社会科学领域中,对于这些领域中的求解问题,常用Gauss-Markov模型或是离散动态模型进行建模,而最小二乘估计(Least Squares Estimate, LS)和卡尔曼(Kalman)滤波分别是两种经典模型解算方法。测量系统的病态性通常表现为误差方程系数矩阵具有复共线性[1],LS估计和Kalman滤波估计都存在估计方差膨胀导致参数估值不稳定的现象。自Gauss(高斯)提出最小二乘法开始,最小二乘估计理论在测量数据处理中得到广泛的应用,最小二乘估计是测量平差的基础方法,顾及观测向量的随机误差,其平差准则是观测向量的残差平方和达到最小[2-3]。对于系数矩阵也存在误差的函数模型通常称为EIV(Errors-In-Variables)模型,则需要采用总体最小二乘估计(Total Least Squares, TLS),其平差准则是观测向量和系数矩阵两类残差的平方和最小,平差理论更为合理[4-6]。对于EIV模型的解算研究,国外学者Gene提出在EIV模型下总体最小二乘问题的奇异值分解(Singular Value Decomposition,SVD)解法,推导出在系数矩阵的谱分解下参数的求和解式,缺陷在于并没有消除或者削弱设计矩阵的病态性,只是对参数估计进行分开按照求和公式进行求解[4];Burkhard基于拉格朗日乘数法导出加权总体最小二乘的迭代求解公式,迭代计算过程复杂,计算量偏大,不利于编程实现[7],同时基于Gauss-Helemert模型,通过对非线性观测方程中随机误差和待估参数进行线性化,由经典最小二乘法导出未知参数的迭代解式[8]。学者沈云中引入非线性最小二乘的Newton-Gauss法,导出加权总体最小二乘的迭代解式的同时还提出一种评定估值精度的数值算法[9]。
在大地测量和地球物理等领域的测量数据处理模型中,参数估计往往伴随着先验信息,此时传统的参数估计问题即扩展为附有约束条件的参数估计,利用参数间一些精确已知的先验等式约束信息也可以显著提高解的准确性和精度,因此在病态总体最小二乘问题中,附加正确的等式约束也能够提高其解的准确性和精度[10-11]。对于附有等式约束的EIV模型,国外学者Burkhard和Yaron研究了附有线性等式约束和二次型约束的等权总体最小二乘问题并基于拉格朗日乘数法导出参数的迭代计算公式[13-14]。但是,约束信息有可能会是相关的,约束方程就会出现病态,使得约束矩阵的微小扰动就会导致最终的反演结果产生极大变化,从而导致反演结果极不稳定,学者王乐洋等人讨论了在具有病态性质约束矩阵的等式约束反演问题,并利用SVD方法来处理约束矩阵的病态性,有效解决约束矩阵病态造成的反演结果极不稳定的问题[15],同时还提出了在附有病态约束矩阵的等式约束反演问题的岭估计解法,利用岭参数来改变系数矩阵的病态性,提高参数解的可信度,使得反演效果良好,同时也带有岭估计统一改正的不足[16]。马洋、欧吉坤等人验证了降秩法与奇异值截断法的基本等效性,针对附有病态约束的反演问题,提出了主模型与约束条件联合解算的新方法,这种方法可以解决主模型病态甚至秩亏的问题,但丢失了部分原始成分信息[17]。为了保留先验信息的完整性,文中在总体最小二乘平差准则的基础上,考虑精确线性约束条件,利用修正奇异值法对病态设计矩阵的奇异值进行分区别修正,导出在精确约束条件下的病态总体最小二乘迭代解式,并进行参数估值的精度评定。
1 总体最小二乘的SVD模型
总体最小二乘的EIV模型为[5]:
L+el=(B+EB)X.
(1)
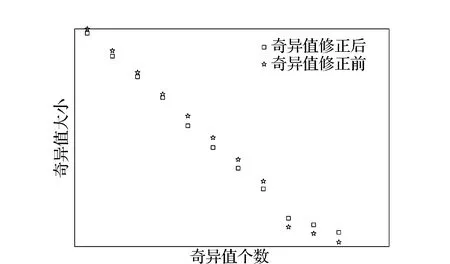
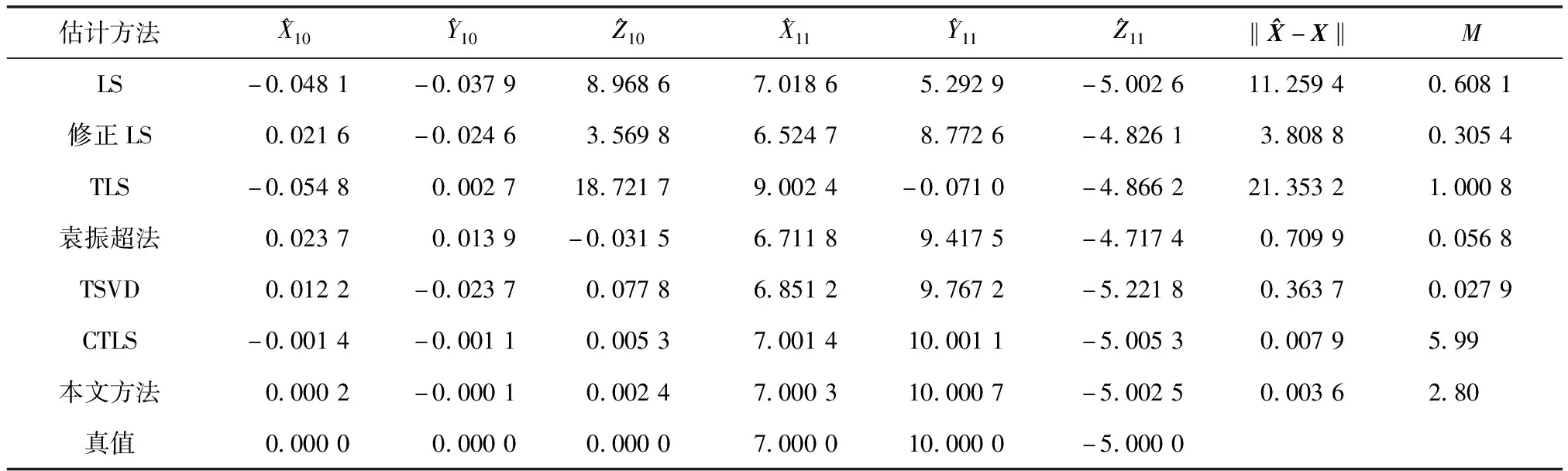
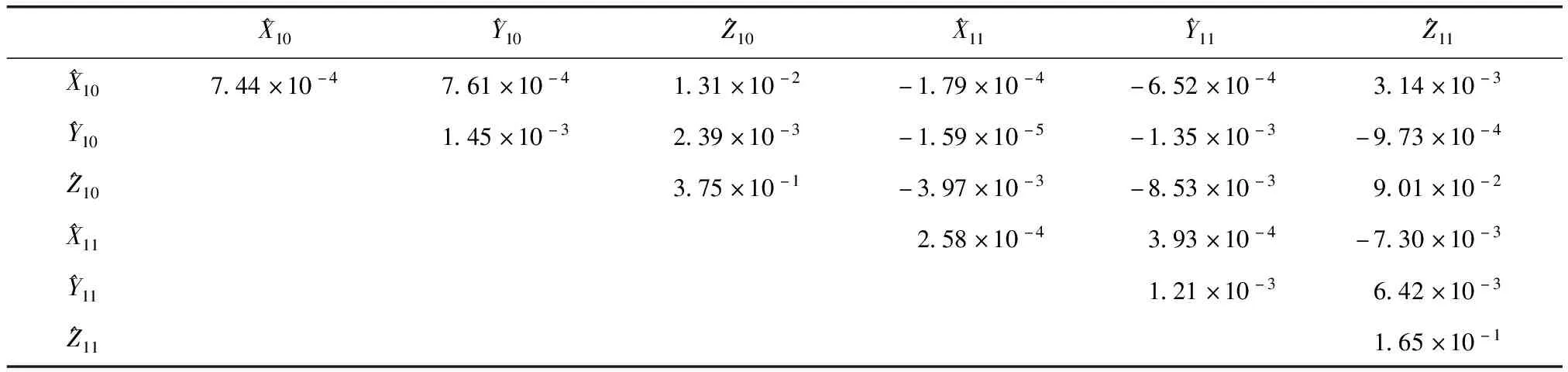
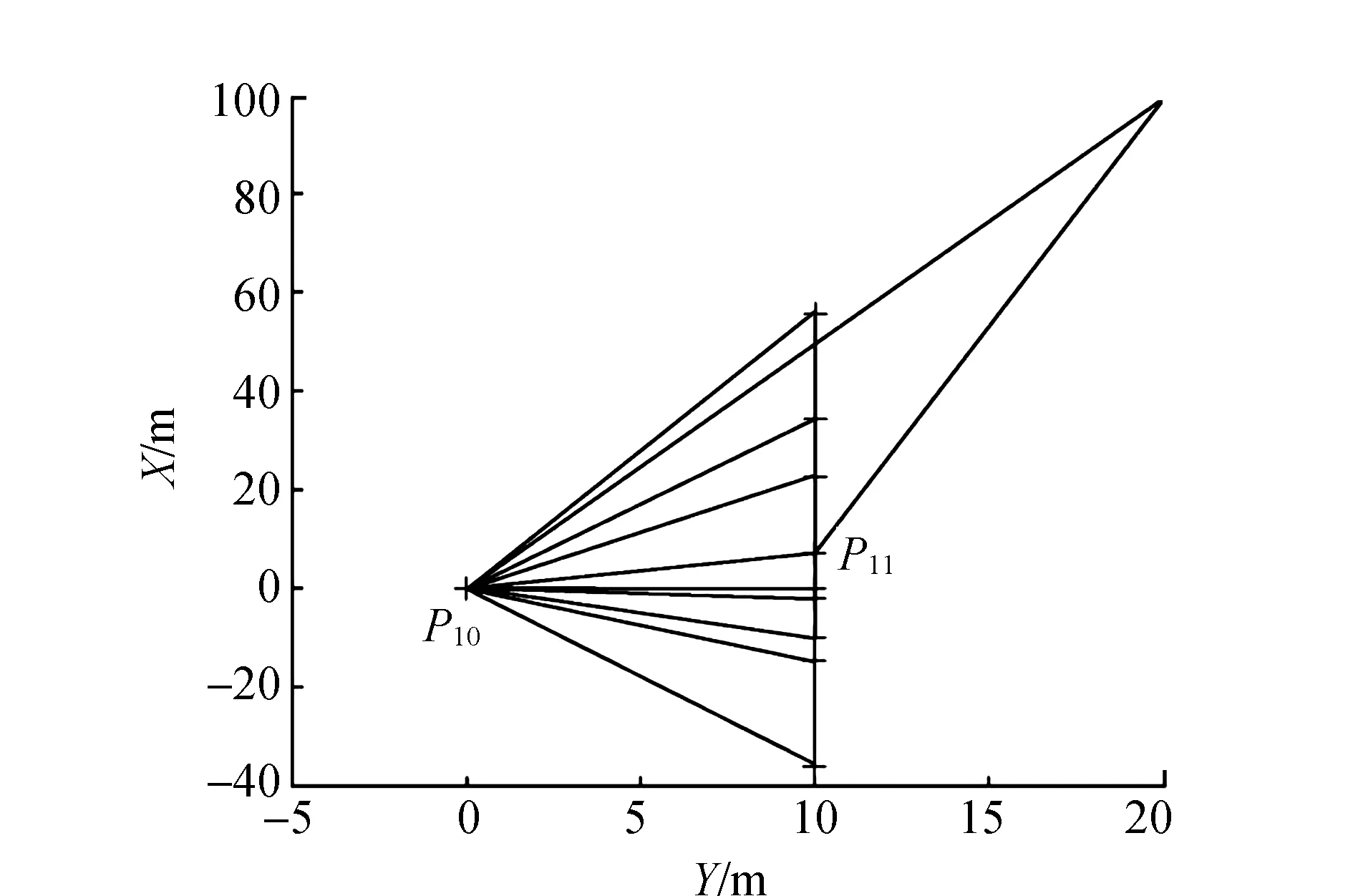
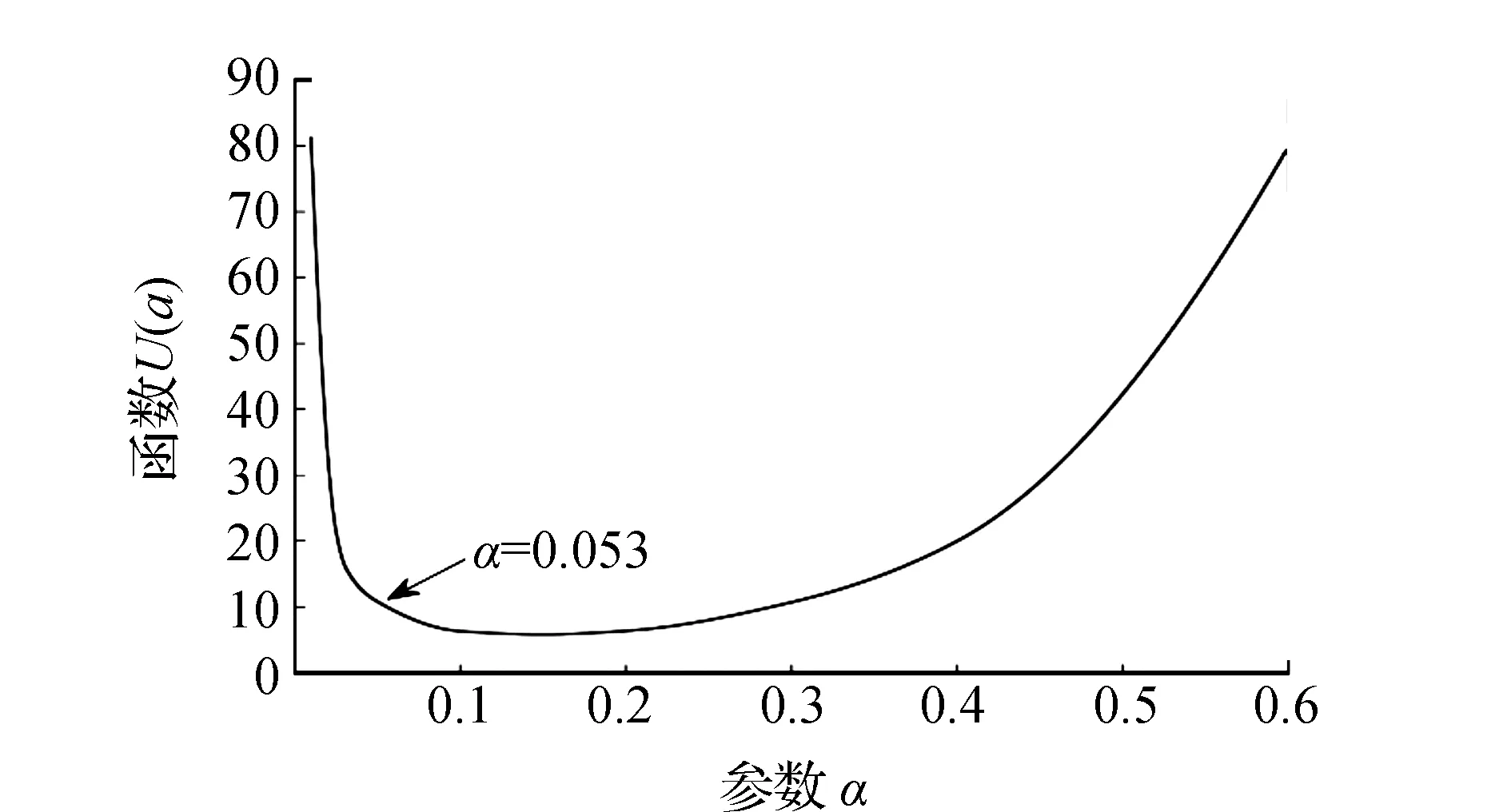
式中:L为观测向量;B为设计矩阵且R(B)=m (2) 其中, eB=vec(EB), L=BX+e. (3) 根据总体最小二乘平差准则,模型(1)的求解式为: 在观测向量和设计矩阵元素的权阵均为单位阵Pl=Im×n,PB=In×m时,求解式变为: (4) 当N=BTB病态情况不容乐观,如在条件数rand(N)≥1 000时,最小二乘估计的参数值变得不可靠。为了参数估计值的稳定性,设法削弱法矩阵的病态性用以获得稳定、可靠的法矩阵逆阵,采用截断奇异值法来处理总体最小二乘估计。 将B矩阵进行奇异值分解,得到[15]: B=UΣVT. (5) 式中:U为n×m阶矩阵;V为m×m阶矩阵;均为正交矩阵。Σ为n×m阶对角阵;对角元素为B的奇异值,按照降序排列,Σ=diag(λ1,λ2,…,λm)。将式(5)代入到LS参数估计中,并做谱展开有: (6) 式中:vi和ui分别是V和U的第i列向量;λi是B的第i个奇异值。通过式(6)看出在奇异值较小的时候,最小二乘估计解值被严重放大,截断奇异值主要在于将小的奇异值截断,避免了小奇异值对参数估计造成大的影响,若去掉后(n-k)个奇异值,则总体最小二乘的截断奇异值解为: (7) 等式约束下的EIV病态模型为[4-6]: L+el=(B+EB)X, h=HX. (8) 式中:H为p×m阶约束矩阵,h为p×1阶约束常数项,且有rank(H=p (9) 其中,μ为p×1阶拉格朗日因子,令 表示为: (10) 根据文献[5]可知: (11) 组合式(10)、式(11)和式(8)可表示为: (12) 奇异值的修正要选取最小奇异值门限,设k为选取参数,将式(5)中的U,Σ,V进行矩阵分块,得到: (13) 在进行奇异值分解后,相对较大的奇异值及其特征向量在参数模型解算中更可靠,相对较小的奇异值及其特征向量在解算过程中不太可靠。截断奇异值法在于去除参数模型中的不太可靠部分,即删掉相对较小的奇异值,从而减少解的方差,同时这会损害解的分辨率。若是奇异值呈现出如图1所示的阶梯状时,截断奇异值法比较适用参数估计,确定可靠成分和不可靠部分差别很大,截掉不可靠部分的奇异值对解的分辨率影响不大。Hansen从理论上证明了当奇异值分布呈现阶梯状时,截断奇异值的方法与岭估计的方法基本上是等价的。奇异值如图1所示呈现的阶梯状且均匀分布,不可靠部分和确定成分的界限不好确定,难以确定截断参数,建议采用奇异值修正法。 图1 奇异值分类示意 奇异值的修正方法为:设t为截断奇异值保留最小奇异值的门限,T为对应的小于t的奇异值个数,进行奇异值的修正[18]: (14) 修改后的奇异值变成 (15) 由于式(12)中系数矩阵和特征向量均存在未知估计参数,因此需要利用迭代法求解,求解过程如下: 2)根据式(12)得到: 其中,“:=”意思是“定义为”,将式(15)奇异值修正结果重新代入到模型式(6)中,再将LS估计值作为初始值参与迭代计算,迭代的次数就是修正奇异值参与的次数,就是病态精确约束总体最小二乘的修正奇异值解。 在病态方程中的法矩阵N的条件数大于1 000时,病态性较为严重,根据病态性情况结合条件数的定义[18]: (16) 在cond(N)2>1 000时,这里的范围数可根据实际情况调整,即奇异值λk(k=1,2,…,n-1)满足: 选取的奇异值最小门限为: t=λk. (17) 在精确约束条件下病态总体最小二乘的修正奇异值解的单位权方差为[5]: (18) 需要说明的是,由于在附有精确约束下的病态总体最小二乘问题中,未知参数的估计值采用的是迭代求解,未知参数与观测向量无法分离,加上设计矩阵也是随机矩阵,本身也存在误差,因此在这种情况下的单位权方差无偏估计计算相对复杂,借助有偏残差估计的单位权方差,即式(18)的单位权方差是有偏的。根据协方差的传播率得出参数的协方差矩阵为: (19) 分块矩阵形式为: (20) 采用GPS动态定位的解算,取历元间隔时间为2 s,观测了5颗卫星,用4个历元解算整周模糊度,误差方程的系数矩阵为[19]: (21) (22) 表1 不同方法参数估计结果比较 表2 参数估计值的方差-协方差阵 图2 U曲线法确定正则化参数α 表3 真实坐标与近似坐标 m 表4 边长观测值(观测向量和设计矩阵, 图3 三角形网 图4 U曲线法确定正则化参数α 表5 不同方法参数估计结果比较 表6 参数估计值的方差-协方差阵 表7 不同方法参数估计结果比较 表8 参数估计值的方差-协方差阵 图5 空间测边网的平面分布图 图6 U曲线法确定正则化参数 参数估计的精确度容易受到误差方程的系数矩阵病态性影响,在病态性较为严重时,LS估计值近乎失真,其与真值的差值范数也较大;根据3个算例的计算结果得知,TLS在病态性较为严重时估计的结果也不理想,此时可以考虑总体最小二乘的截断奇异值法或总体最小二乘的正则化法。CTLS方法比较依赖于等式约束条件的系数矩阵,同时又受到误差方程系数矩阵的影响。修正奇异值法的直观展现在于进行一次奇异值修正时,参数估计值与真值的差值范数为: 算例1: 算例2: 算例3: 进而使得参与迭代计算的初始值经过奇异值修正后有所改善。 参数估计的先验信息能够提高参数估计解的准确性和精度。在等式约束下,提出了病态总体最小二乘估计的修正奇异值解法,利用总体最小二乘准则和协方差传播率推导出在等式约束下的总体最小二乘迭代式;并借助有偏残差估计的单位权方差,通过协方差的传播率得出参数的近似协方差矩阵。用数值分析算例和测边网算例验证文中方法,并与TSVD、TLS和CTLS等参数估计方法作比较,证明文中方法在奇异值按照降序排列且成阶梯均匀分布时,用于对参数估计精度提升最有利,文中方法在于保持参数估计解的分辨率同时顾及解的精度提升。文中只做了在等式约束下总体最小二乘奇异值修正,后续将进一步研究在随机约束、不等式约束下的总体最小二乘奇异值修正方法。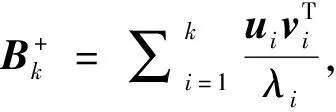
2 等式约束条件总体最小二乘模型
2.1 等式约束总体最小二乘的修正奇异值解

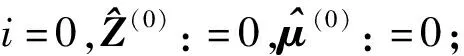

2.2 最小奇异值门限的确定
2.3 精度评定
3 算例及分析
3.1 整周模糊度算例
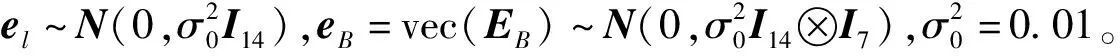
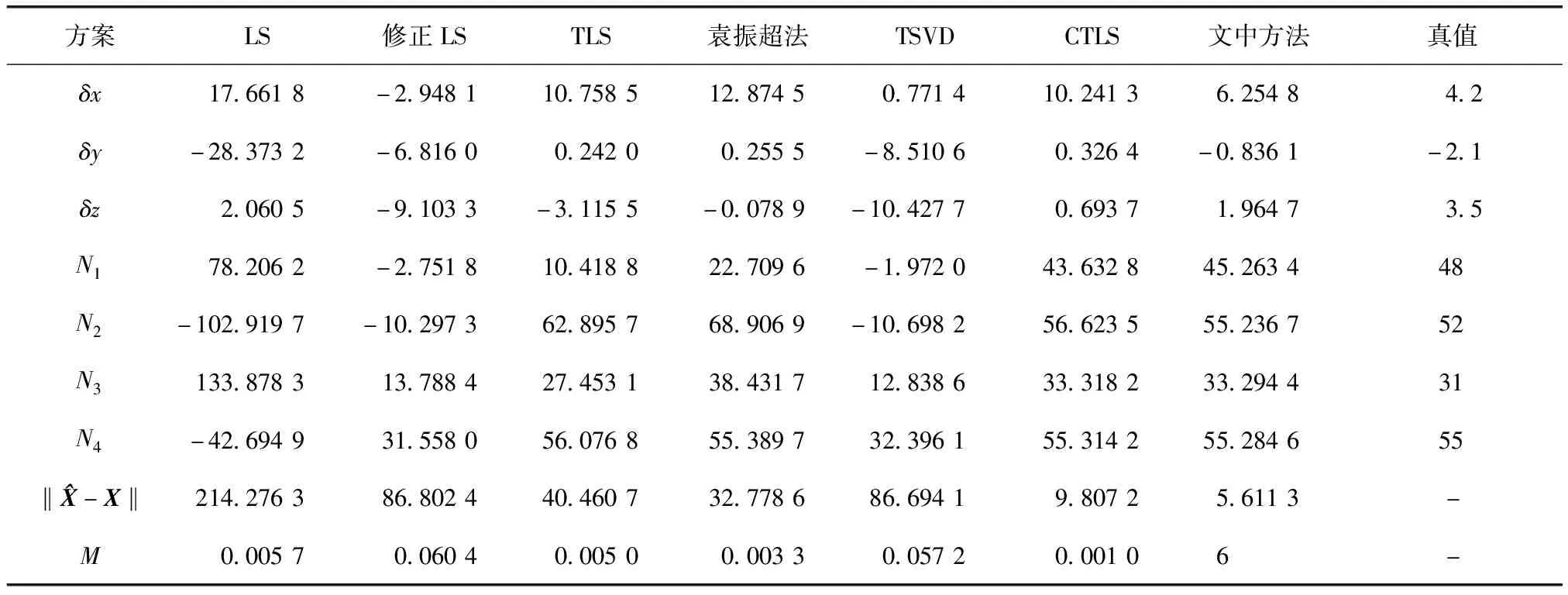
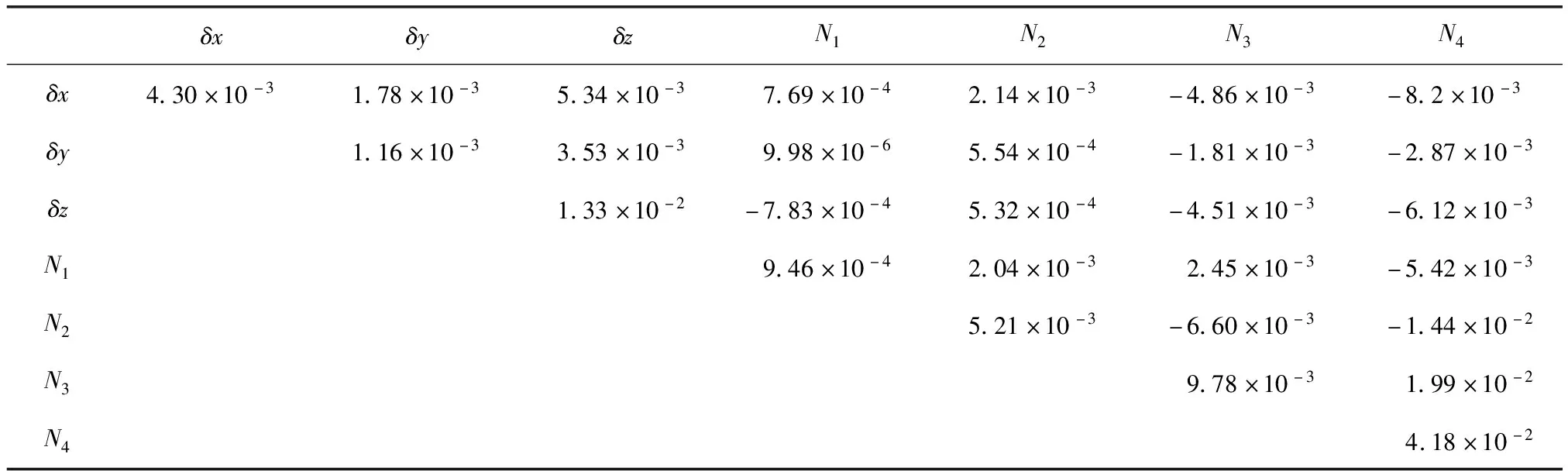
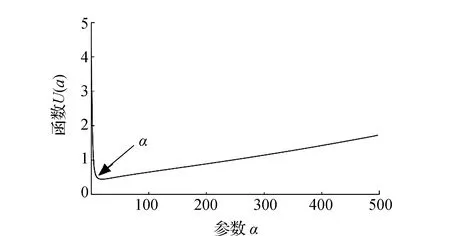
3.2 测边网算例
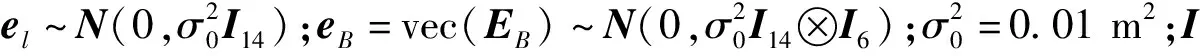

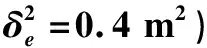
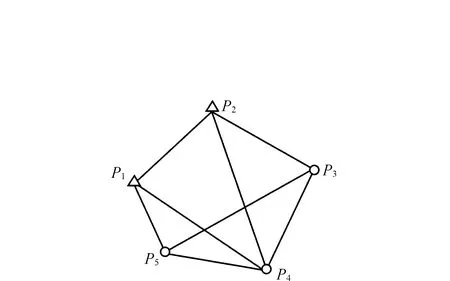


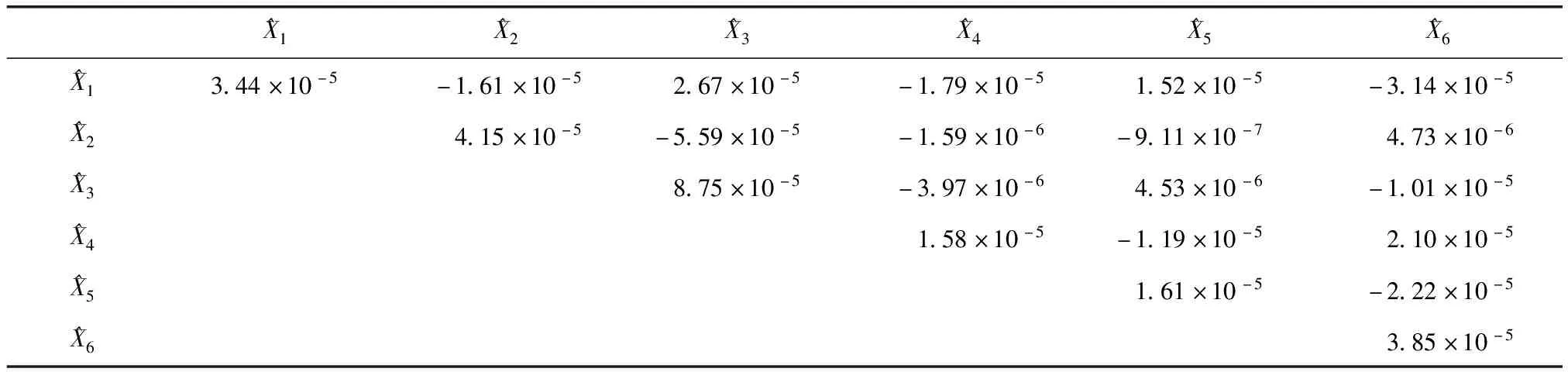
3.3 病态网算例
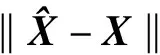


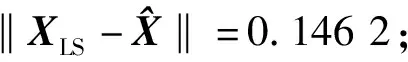
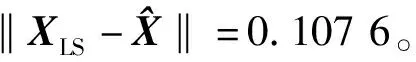
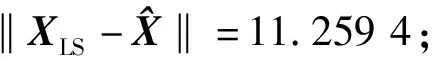
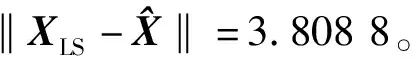
4 结束语

