二维有界区域上具有非线性梯度项的抛物系统解的存在性
李远飞
(广州华商学院数据科学学院,广东 广州 511300)
1 引言及准备工作
本文研究具有非线性梯度项的耦合反应-扩散方程:
(1)
(2)

(3)
u(x,0)=u0(x),v(x,0)=v0(x),x∈Ω,
(4)
0≤g1(ξ,η)≤ξp1ηq1, 0≤g2(ξ,η)≤ξp2ηq2,
(5)
其中p1,p2,q1,q2是大于零的常数且0 在过去的几十年中,关于线性和非线性抛物方程解的存在性以及爆破现象一直是人们关注的焦点.事实上,方程(1)—(4)的几种特殊形式已经得到了研究.2003年,Wang[4]研究了非线性边界条件下的半线性抛物方程 ut=Δu+up,vt=Δv,x∈BR,t>0, u(x,0)=u0(x),v(x,0)=v0(x),x∈BR, 其中Δ是拉普拉斯算子,BR是N上的一个半径为R的球,n是∂BR上的外单位法向量.对方程中的参数做出一定的限制之后,得到解的爆破率的上界和下界.Chen[5]则把文献[4]的结果推广到了热量方程 ut=Δu,vt=Δv,x∈Ω,t>0, u(x,0)=u0(x),v(x,0)=v0(x),x∈Ω. 2013年,Xu等[6]考虑了以下耦合反应-扩散问题: ut=Δu+upvq,vt=Δv+urvs, (x,t)∈Ω×(0,t*), u=v=0, (x,t)∈∂Ω×(0,t*), u(x,0)=ρu0(x),v(x,0)=ρv0(x),x∈Ω. 该系统模拟了各种物理现象,例如描述了热在双组分连续介质中的扩散和燃烧过程、电导率、体积能量释放和核爆炸. 本文研究方程(1)—(4)的爆破现象和全局存在性.当爆破发生时,推导爆破时间的下界.事实上,不管爆破最后有没有发生,这种下界都是有意义的.例如文献[8]提到的2003年哥伦比亚号航天飞机的灾难.由于航天飞机发射时被一块脱落的泡沫击中飞机左翼,导致隔热材料局部受损.结果,在重返大气层时,航天飞机由于在受损部分附近产生的巨大热量而解体.事实上,以前的几架航天飞机也有类似的问题,但它们都能安全着陆.一些工程师怀疑这些损伤太小,航天飞机在温度变得足够高之前已经着陆.更多关于解爆破性研究和解存在性研究的最新成果,参见文献[9-16]. 本文重点研究当N=2时耦合反应扩散方程(1)—(4)爆破时间的下界.受文献[7]的启发,本文通过定义稍微不同的辅助函数,利用一阶微分不等式技巧和能量估计的方法,推导爆破时间的下界.并且推导了解全局存在的充分条件. 引理1[17]设Ω是N,N≥2上的有界星型区域.若w∈C1(Ω),则有 其中ρ0=min∂Ω(x·n),d=max∂Ω|x|,n>1. 利用Hölder不等式,可得 (6) 利用不等式 (a+b)l≤max{1,2l-1}(al+bl),a,b>0, 0 和式(5),由引理1可得 (7) 引理2[16,18]设Ω是2上的有界凸区域.则存在依赖于Ω及其边界∂Ω大于零的常数Λ1使得 其中δ1是大于零的任意常数.所以 (8) 取δ1足够小并对区域Ω做适当的限制使得 由式(8)可得以下引理. 引理3设Ω是2上的有界星型区域.若w∈C1(Ω),则有 利用上一节给出的引理,本节推导爆破发生时爆破时间的下界.为此,建立以下辅助函数: (9) 首先对φ(t)求导,再利用散度定理和方程(1)—(4),可得 I1+I2+I3+I4+J1+J2+J3+J4. (10) 利用Hölder不等式、Young不等式和式(7)并注意到0 其中kij,i,j=1,2是大于零的常数,ε1,ε2是大于零的任意常数.记 则由式(11)可得 (12) 类似地,当0 (13) 其中ε3,ε4,ε′3,ε′4是大于零的任意常数. 利用Hölder不等式, Young不等式和引理2,可得 其中ε3是大于零的任意常数, 其中ε4是大于零的任意常数. 下一步我们考虑0 (17) 其中c′7是大于零的常数. 显然 (18) 再利用引理3,由式(18)可得 (19) 类似地,有 (20) 由式(19)和(20),可得 (21) 若0 (22) 取适当的ε1,ε′1,ε2,ε′2,ε3,ε4使得 (23) 由式(22)可得 (24) (25) (26) (27) (28) 其中θi(i=1,2,3,4)是大于零的任意常数, 取适当的θi(i=1,2,3,4)使得 c12θ1+c′12θ2+c22θ3+c′22θ4=c8, 再把式(25)—(28)代入到式(24)得 (29) 其中c9=c11+c′11+c21+c′21. 如果方程的解在某有限时刻t*发生爆破,即limt→t*φ(t)=∞,对式(29)从0到t*积分可得爆破时间的下界.此结果总结为以下定理. 定理1设u和v是方程(1)—(4)的非负解,其中Ω是2上的一个有界光滑的凸区域,g1,g2满足式(5)且0 (30) 注1由于式(30)右边分母中后四项的指数都是大于1的,所以式(30)右边的积分是收敛的. 注2如果0 (31) 又由于 (32) (33) 其中θ5,θ6是大于零的任意常数, 把式(24)—(27)和式(32)、(33)代入到式(31)并取θi(i=1,2,…,6),得 c12θ1+c′12θ2+c22θ3+c′22θ4+c′qθ5+c′(s,r)θ6=c8, 进而得 (34) 其中c9=c11+c′11+c21+c′21+cq+c(s,r).与式(29)类似,我们可得以下定理. 定理2设u和v是方程(1)—(4)的非负解,其中Ω是2上的一个有界光滑的凸区域,g1,g2满足式(5)且0 类似地,当0 定理3设u和v是方程(1)—(4)的非负解,其中Ω是2上的一个有界光滑的凸区域,g1,g2满足式(5)且0 注3若0 (35) 如果方程(1)—(4)的解在φ(t)的测度下在某有限时刻t*处发生爆破的话,由式(35)可知必存在一个时刻t0 定理4设u和v是方程(1)—(4)的非负解,其中Ω是2上的一个有界光滑的凸区域,g1,g2满足式(5)且0 注4如果方程(1)和(2)由方程 (36) (37) 代替,只要限定0 本文研究了具有非线性边界条件下,当N=2时一类抛物方程解的爆破现象,通过对方程中的参数进行一定的限制,得到了爆破解的下界,并获得了全局解的存在性.同时我们注意到当N≥3时,引理2就不再成立了,此时可以利用文献[19]获得一个微分不等式. 利用此不等式,我们可以继续研究问题(1)和(2),或(32)和(33)解的存在性和爆破现象.2 重要引理

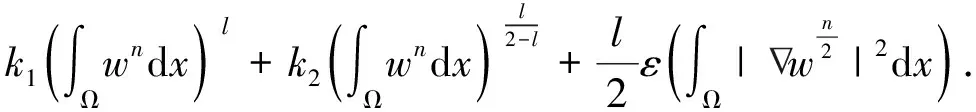


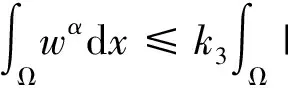

3 N=2时解的爆破现象

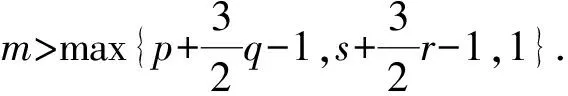

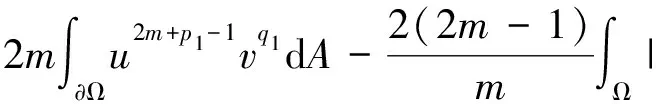

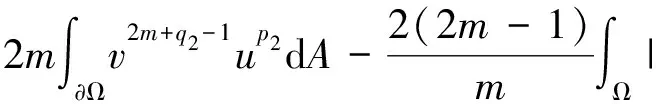



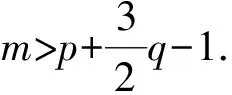


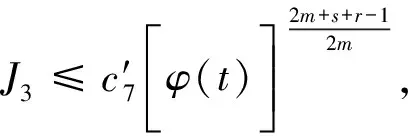



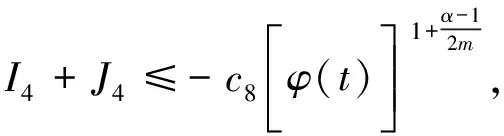
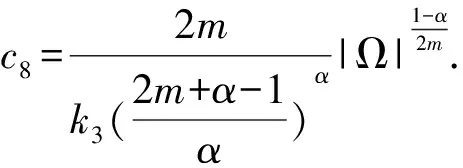
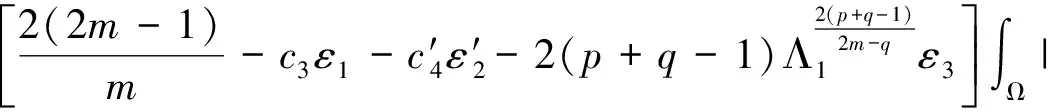
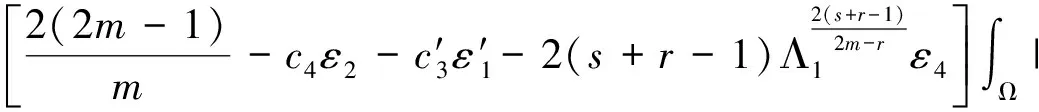
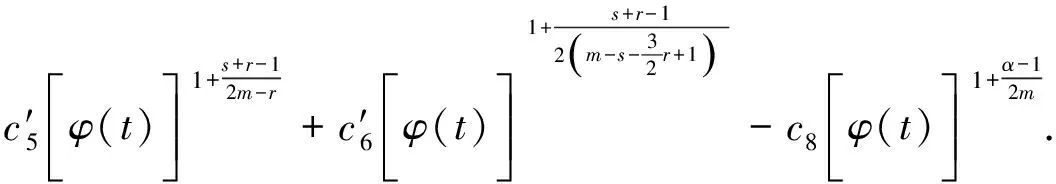
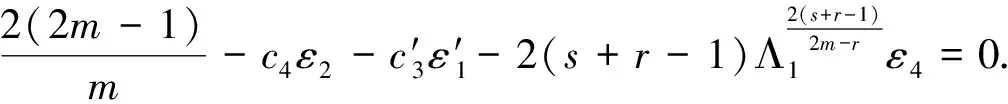
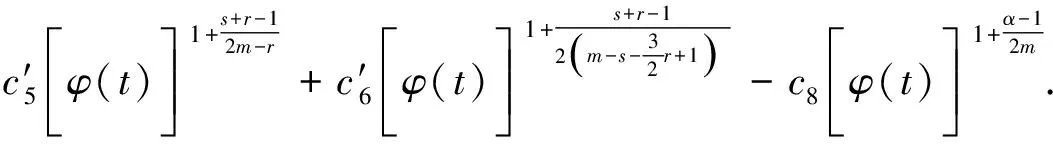
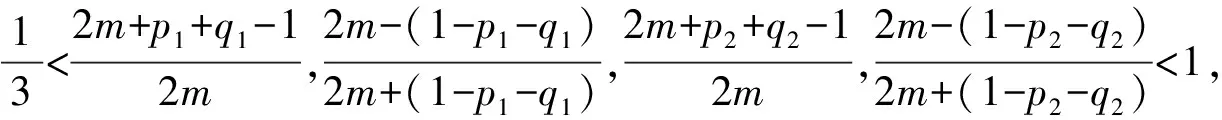



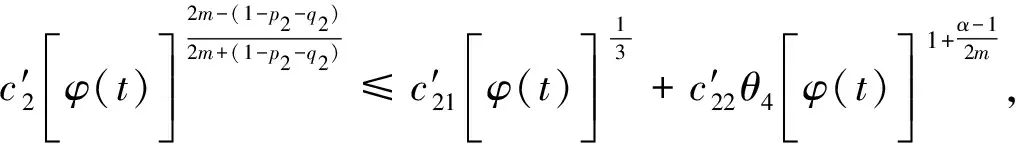

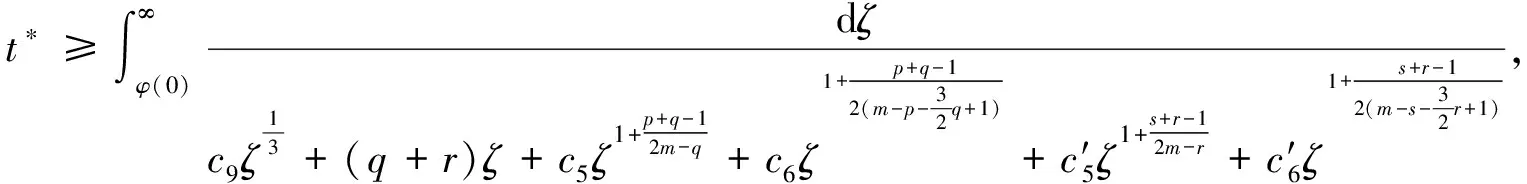
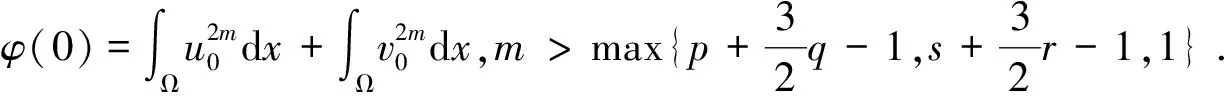
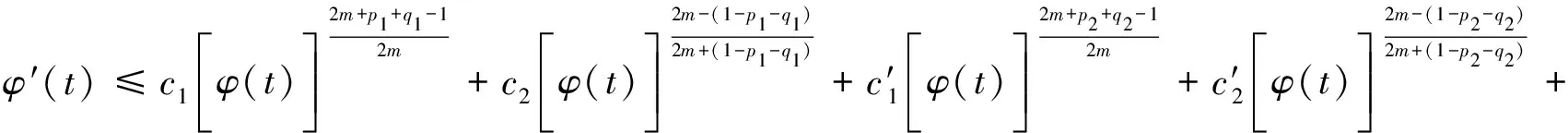
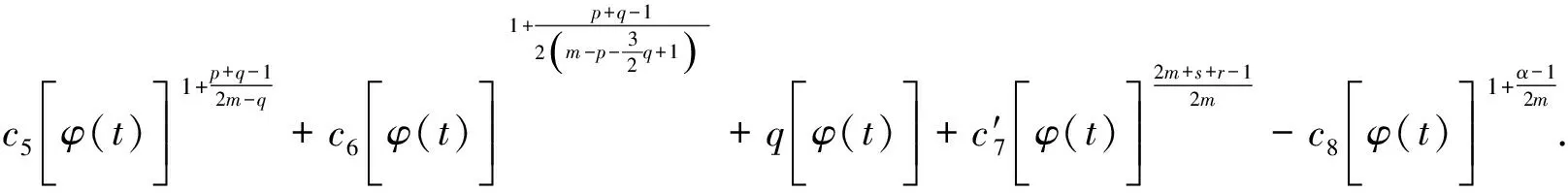
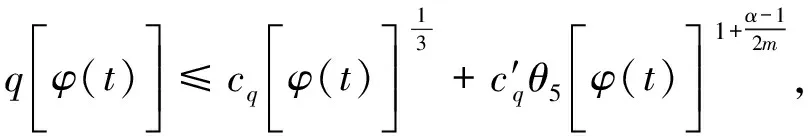





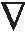
4 结论

