高精度液压系统压力波传递速度在线测量试验*
梁云栋,何 琳,徐荣武,陈宗斌
(海军工程大学 船舶振动噪声重点实验室, 湖北 武汉 430033)
液压管路压力波传递速度,简称压力波速,是液压工程中非常重要的一个基本物理参数。它反映了流体的可压缩性、黏性等特性,直接影响了系统的固有频率和阻尼比,从而间接反映了液压系统的稳定性和动态品质。
然而对于实际液压系统,影响压力波传递速度的因素很多,它不仅与流体本身的物理性质有关,包括液压油的压力、温度、分子结构和含气量等;而且受管道的几何参数、材料的机械性质及结构支承方式的影响。在液压系统流体传输过程中它始终是个变量,因此准确地确定液压管道内的压力波传递速度是一大难题,目前国内外在工程应用上均视其为常量,在计算机动态仿真和液压系统故障诊断等过程中,这种处理常会带来很大的误差。
压力波传递速度测量主要是通过试验手段,试验方法又分为直接测量法和间接测量法[1]。直接测量法是在时域和频域的实时测量中获取压力波传递速度的值;间接测量法是通过确定流体的体积弹性模量来间接地导出压力波传递速度,由于间接测量没有考虑到液压系统动态特性变化,对工程实际的指导意义不大。
为提高直接测量方法的准确性,国外学者针对测试过程做了大量的改进研究,主要包括测量传感器的数量选择,测点之间的布置距离,测试数据后期处理和拟合方法等。20世纪七八十年代开始,Margolis和Brown[2]发明了一种在湍流中测量正弦扰动波传递速度和衰减率的试验方法,将三个压力传感器等距布置在长为137 m的螺旋管上,并证明了波速是频率和雷诺数综合作用的结果。Bolleter[3]用了类似的方法,在1.25 m的长直管道上等距布置三个传感器,这种改进更加方便、实用,可适用于在线测量,但忽略了黏滞摩擦效应和传递波频率变化对试验的影响。英国Bath大学的Johnston和Edge[4]在此基础上做了创造性工作,他们将测量方法扩展到非等间距传感器测量试验,并且在处理数据过程中考虑了流体的黏性、热传递和摩擦效应,但是对影响因子特性考虑并不充分[5-11],其优点在于避免了当传感器间距恰好为传递波半波长整数倍时导致测量数据失效的问题。更进一步地,Johnston的方法作为两种方法之一被ISO 15086-2: 2000[9]所采用,相比于双传感器测量方法所需的苛刻试验条件,此法被推荐适用于在“任何时间和任何正常有效工作条件下液压系统”的压力波速在线测量。其他方法有Karjalaine等[12]和Yu等[13]基于测量两个压力波延迟的互相关法,试验方法简单但高度依赖于充分高的激励频率和采样频率,试验结果易受反射波的影响且准确性尚不清楚。Yu等[14]和中川修一等[15]对现有的波速测量方法进行了很好的回顾并且提出了一种利用等效替换思想来测量液压系统部件中压力波速的方法,在试验测量方法本质上并没有创新。国内学者在此基础试验测量研究上做的工作相对较少,鲜有相关文章、报告和试验,尚未有人给出准确压力波速值为当前的液压系统动态仿真和研究提供参考。
针对当前研究对管内流体影响因子特性考虑还不够充分和国内尚未明确给出准确的液压系统压力波速参考值这两个问题。本文从传输管路波动方程出发,推导三传感器测量原理,引入Foster等价剪切系数模型对液压管路中各种影响因子进行了高精度估计,采用Newton-Raphson迭代法减小数据处理误差,以精确计算压力波传递速度。搭建液压管路压力波速在线测量试验平台,用MATLAB软件编程,实现了液压系统多种工况下压力波速的精准测量与计算。
1 理论分析
从流体传输管路波动方程出发,推导三传感器测量原理,引入Foster等价剪切系数模型对液压管路中各种影响因子进行高精度估计,采用Newton-Raphson迭代法精确求解压力波传递速度。
1.1 传输管路波动方程
根据流体传输管路波动方程[1]:
(1)
由式(1)解得:
(2)
式中:P(x,s)、Q(x,s)分别为管道上任一点x处瞬时体积流量和流体压力的拉普拉斯变换;z0为管路特征阻抗;γ为波传播系数,表示波在传播过程中的幅度衰减和相移特性,通常为复数;F和G是由边界条件所决定的系数。
1.2 三传感器测量原理推导[3]
测试液压系统原理如图1所示。
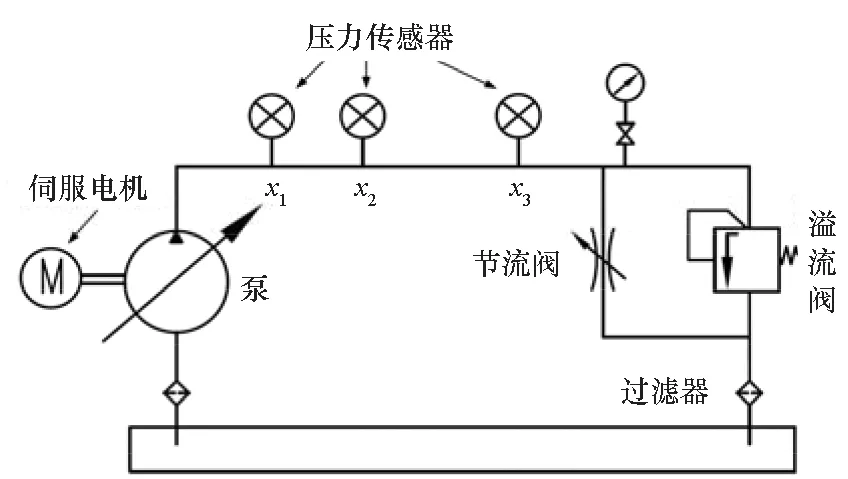
图1 测试液压系统原理图Fig.1 Test hydraulic system schematic diagram
以泵出口处为坐标原点,通过调节伺服电机的转速N来改变管路中压力波的激励频率,在长直管道上依次布置三个动态压力传感器测量管路在该点的瞬态压力,调节节流阀开度大小改变系统的工作压力,溢流阀对系统起到安全保护作用,过滤器过滤掉液压油中的杂质。三个传感器的坐标依次为x1、x2、x3,所测压力波激励频率下第i次谐波的瞬态压力分别为P1,i、P2,i、P3,i。
由式(2)可得:
(3)
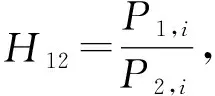
(4)
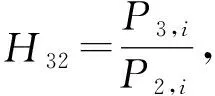
(5)
联立式(4)~(5)可得如下双曲正弦方程:
H12sinh[γ(x3-x2)]+H32sinh[γ(x2-x1)]-
sinh[γ(x3-x1)]=0
(6)
方程(6)中,x1、x2、x3和H12、H32均为已知量,波传播系数γ由下文介绍的传输管路频率特征模型给出。
1.3 传输管路频率特性模型
根据假设条件不同,流体传输管道一般分为三种模型:无损模型、线性摩擦模型以及耗散模型。
在工程实际测试中,对于长直液压管路,一般认为流体运动为层流,充分考虑流体的黏性和热传递效应。在该假设条件下,通常选用耗散模型,在频率为f的正弦激励波下,波传播系数给定如下[1]:
γ=j2πfξ/c0
(7)
其中:ξ为管道修正系数,反映管路的黏滞效应,c0为本文所需测量的压力波传递速度。由式(7)可得管道修正系数为:
(8)
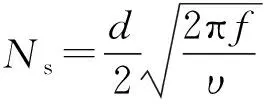
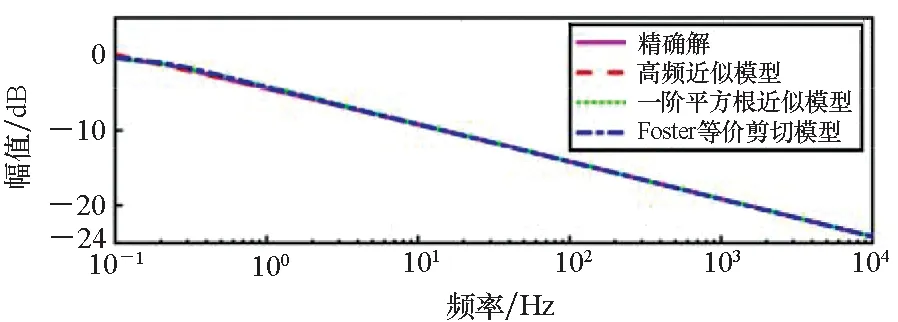
由式(8)可知,耗散模型引入了贝塞尔函数,增加数据处理难度的同时高频段计算结果还会显示出不稳定性,常见较为精确的近似方法有Foster等价剪切系数模型、高阶近似模型及一阶平方根近似模型[1],三种模型计算方式下ξ的频率响应与贝塞尔函数精确解的对比曲线如图2所示。
(a) 幅频响应(a) Amplitude-frequency response
由图2可知,Foster等价剪切系数模型在全频段,尤其是低于10 Hz的低频段,与贝塞尔函数精确解的幅值和相位响应曲线重合度最高,优于其他模型,本文数据处理过程中选用该模型。
采用Foster等价剪切系数模型近似后,管路修正系数为[1]:
(9)
其中,K1和K2是与Ns有关的表达式,按照如下规则取值:
(10)
(11)
1.4 Newton-Raphson迭代法求解压力波速
将式(7)代入方程(6),可得:
(12)
利用方程(12)求解出管道压力波传递速度c0。
一方面此方程是压力波速c0的非线性方程,无法直接求解;另一方面由于试验过程中不可避免的各种误差,方程左端式子不为0。为减小试验误差的影响,采集管路压力波激励频率前n阶谐波的压力脉动数据,同时采用Newton-Raphson迭代法[16]处理试验数据,达到使各阶谐波下误差ε的平方和E最小的目的,Newton-Raphson迭代法计算流程如图3所示。
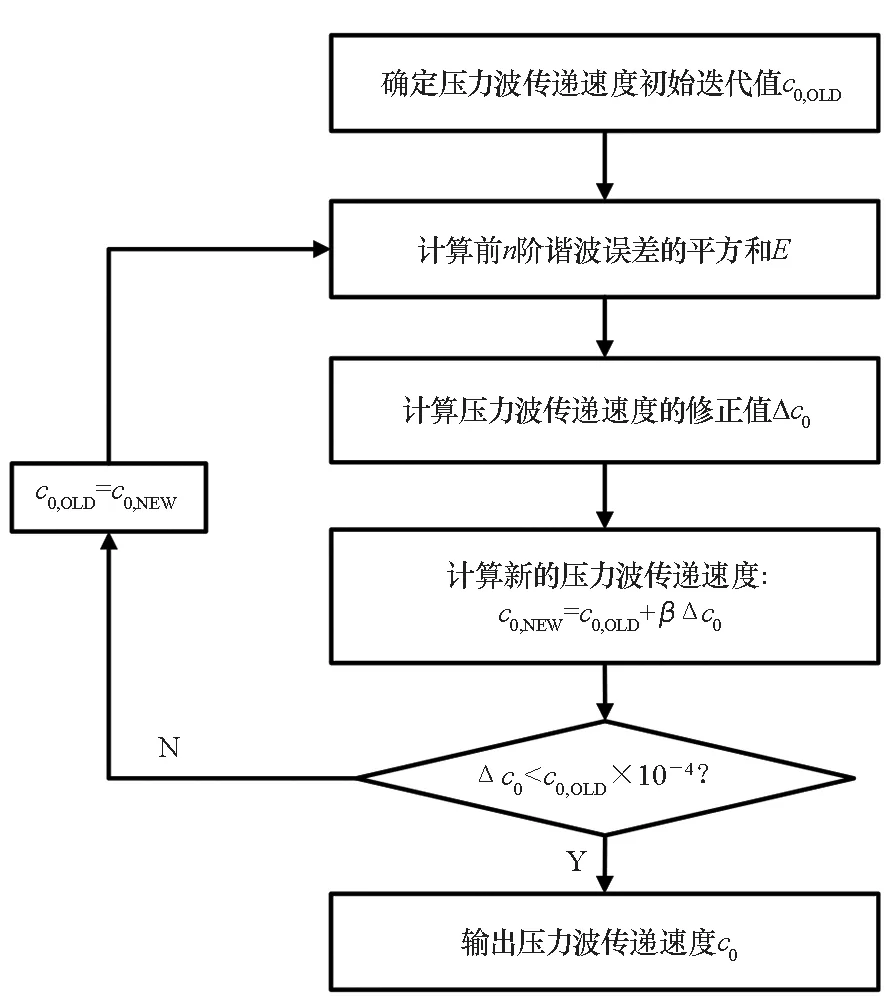
图3 Newton-Raphson迭代法计算流程Fig.3 Calculation process of the Newton-Raphson iterative method
其具体步骤如下:
步骤1:查阅液压油产品说明书并进行相关的校正,得到油液密度ρ和油液等效体积弹性模量Be的估计值,计算压力波传递速度的初始迭代值,即
(13)
步骤2:利用所测试验数据计算出管道压力波下第i阶谐波频率fi处对应的误差:
(14)
误差平方和为:
(15)
由式(13)~(14)可得:
(16)
(17)
步骤3:计算压力波传递速度的修正值,即
(18)
步骤4:计算新的压力波传递速度,即
c0,NEW=c0,OLD+βΔc0
(19)
式中,β为迭代松弛因子,控制迭代过程中的收敛速度和稳定性,通常0<β≤1,这里取β=0.7。
(20)
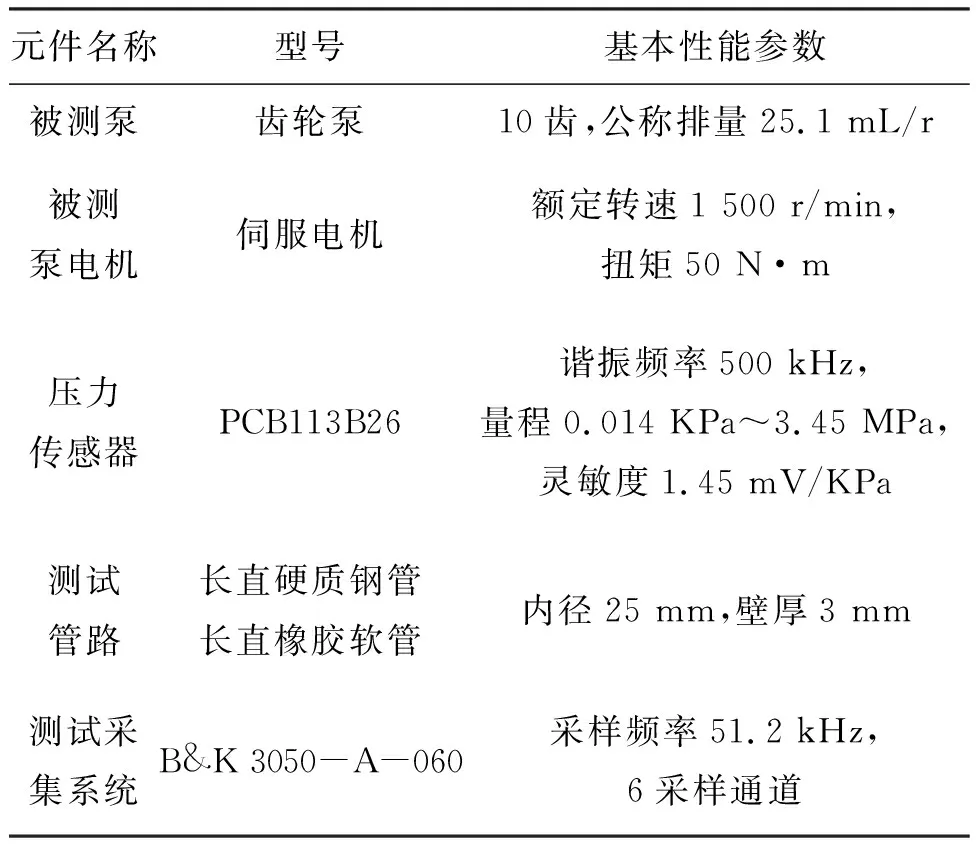
步骤5:判断迭代是否收敛,即收敛条件Δc0 步骤6:最终输出的c0,NEW即为压力波传递速度c0。 本文测试平台搭建以某型齿轮泵作为液压管路系统的激励源,测试管路选取等径长直硬质钢管和橡胶软管,管夹周向包覆弹性支撑,三个传感器非等距离布置在管路上,利用B&K模块对管路中的压力脉动数据进行实时采集,通过可调节节流阀改变系统工作压力,调节伺服电机转速改变管路中压力波的激励频率,通过温度计表头监测系统的工作温度,液压油选用46号抗磨液压油。测试平台选用元器件见表1。 表1 测试平台选用的元器件 试验平台实物图及测点布置见图4。 图4 试验平台实物图及测点布置Fig.4 Physical map of test platform and measuring-point arrangement 调节伺服电机改变泵的转速范围:800~2 000 r/min,转速间隔为100 r/min;调节可变节流阀改变系统的工作压力,本试验选取系统典型工作压力20 bar、50 bar、75 bar、100 bar;更换等径的橡胶软管,重复上述试验。采集系统在各种工况下的压力传感器数据,研究系统压力波速随工作压力以及管路材料的变化规律。 测试管路为硬质钢管时,查阅46号抗磨液压油样本获取液压油密度ρ=876 kg/m3,运动黏度υ=46 mm2/s,油液体积弹性模量B=16 800 bar,将管路壁厚d和内径t、管路杨氏弹性模量E=2 060 000 bar代入式(21)[17],得到考虑管路刚度的油液有效体积弹性模量Be=15 612 bar。测点位置x1=0.1 m,x2=0.43 m,x3=0.9 m。 (21) 剔除掉管路系统共振和此布置条件下测试失效的试验数据。以泵1 000 r/min稳定运行,工作压力50 bar工况为例,具体给出详细处理步骤。首先,通过傅里叶变换将测试采集系统实时采集的时域数据转换为频域数据;其次,利用滤波器提取出管道压力波前20阶谐波的压力脉动P,三个测点的原始时域数据和频域上提取的前20阶谐波的压力脉动幅值分别如图5~6所示;最后,基于MATLAB软件编制程序,计算出各激励频率下前20阶谐波所对应的剪切系数Ns和修正系数ξ,将所求得的P、Ns、ζ代入波动方程,采用Newton-Raphson迭代法计算出此工况下的压力波速。其余工况和橡胶软管测试时采用与之相同的流程和数据处理方法。 (a) 1#测点(a) 1# measuring point (a) 1#测点(a) 1# measuring point 2.3.1 工作压力对压力波传递速度的影响 不同工况下的压力波传递速度试验结果如表2所示,各工况下的压力波传递速度变化曲线如图7所示。 表2 不同工况下的压力波传递速度计算值 图7 各工况下的压力波传递速度曲线Fig.7 Pressure wavespeed curves under different working conditions 液压管路系统压力波传递速度与介质工作压力之间为二次对应关系[18],以1 000 r/min工况为例,对试验数据进行拟合,得到压力波传递速度c0与介质工作压力p(0≤p≤125)之间的函数关系式为: c0=0.001 392p2+0.671 8p+1 301 (22) 由表2的数据可知,在误差允许范围内,相同工作压力下,压力波传递速度大小基本不变。在系统典型工作压力20 bar、50 bar、75 bar和100 bar下压力波传递速度大小分别约为1 320 m/s、 1 338 m/s、1 363 m/s、1 380 m/s。 虽然液压油中含气量极少,但气泡的存在使得油液的有效体积弹性模量降低,从而导致压力波传递速度降低。工作压力逐渐增大,油液中的含气量减小,压力波传递速度随之增大。由图7可知,在误差允许范围内,管路压力波传递速度大小随着工作压力的升高而增大。可见,试验分析结果验证了“压力波传递速度与流体所受到的压力有关,压力越大,波速越大”这一理论分析结论的正确性[1]。 2.3.2 管路材料对压力波传递速度的影响 以泵1 000 r/min稳定运行工况为例,对比分析测试管路分别为硬质钢管和橡胶软管时压力波传递速度的试验结果,如图8所示。 图8 硬质钢管和橡胶软管压力波传递速度试验结果对比Fig.8 Comparison of test results of wavespeed between rigid steel tube and rubber hose 可见,相同条件下考虑管壁结构弹性时,橡胶软管在管内压力作用下产生的弹性形变较大,系统表现出的柔性较强,从而降低系统的压力波传递速度[19]。 由于波速求解方程的非线性和试验过程中不可避免的偶然误差,采用概率统计中的F分布理论对实验结果进行评估,计算出以各工作压力下测量样本均值为中心,置信水平为95%的波速置信区间[20],如表3所示。 表3 不同工作压力下的压力波传递速度置信区间 同时计算出各工作压力下的波速测量结果与样本均值之间的测量误差。以硬质钢管下的测试数据为例,如图9所示,可见,试验分析结果表明在给出的具有95%置信度的波速区间内,误差小于±1%。 图9 各工况下的压力波传递速度测量结果误差Fig.9 Error of measurement results under different working conditions 1)针对现有压力波传递速度测量试验中影响因子估计不足,缺乏准确压力波传递速度参考值的问题,本文推导了非等距三传感器的测量原理,引入Foster等价剪切系数模型,采用Newton-Raphson迭代法求解压力波传递速度,为液压管路压力波传递速度的在线精确测量奠定了理论基础,对液压系统管路压力波传递速度在线测量和评估具有指导意义。 2)基于理论推导,搭建液压管路压力波传递速度在线试验平台,用MATLAB软件编程,实现了对系统多工况下的压力波传递速度精准测量与计算,试验结果表明:在系统典型工作压力20 bar、50 bar、75 bar和100 bar下,压力波传递速度大约分别为1 320 m/s、1 338 m/s、1 363 m/s、1 380 m/s,在置信水平为95%的波速区间内误差小于±1%;管路压力波传递速度大小随着工作压力的升高而增大,并给出二者之间的函数关系,实现了对压力波传递速度的准确估计,为液压系统动态仿真和实际工程计算研究提供重要基础数据支撑。 3)液压管路材料会影响管路系统的柔性,柔性会降低压力波传递速度,在精确计算系统压力波传递速度时,必须考虑管路柔性对压力波传递速度的影响。 4)本文所述试验思路和方法对其他类型流体介质管路压力波传递速度测量具有一定的参考价值。2 试验研究
2.1 搭建试验平台

2.2 试验数据处理
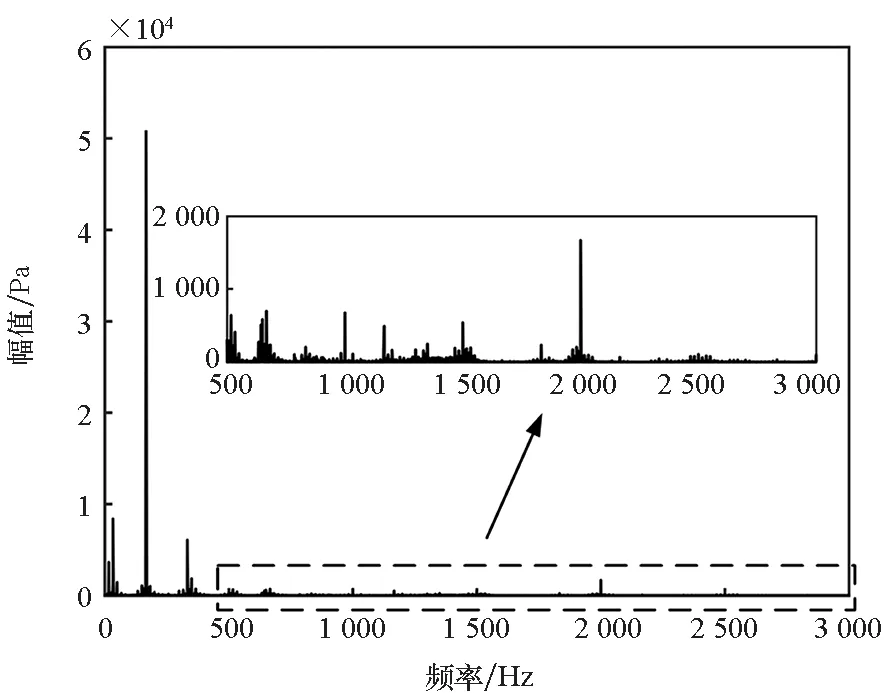
2.3 试验结果分析
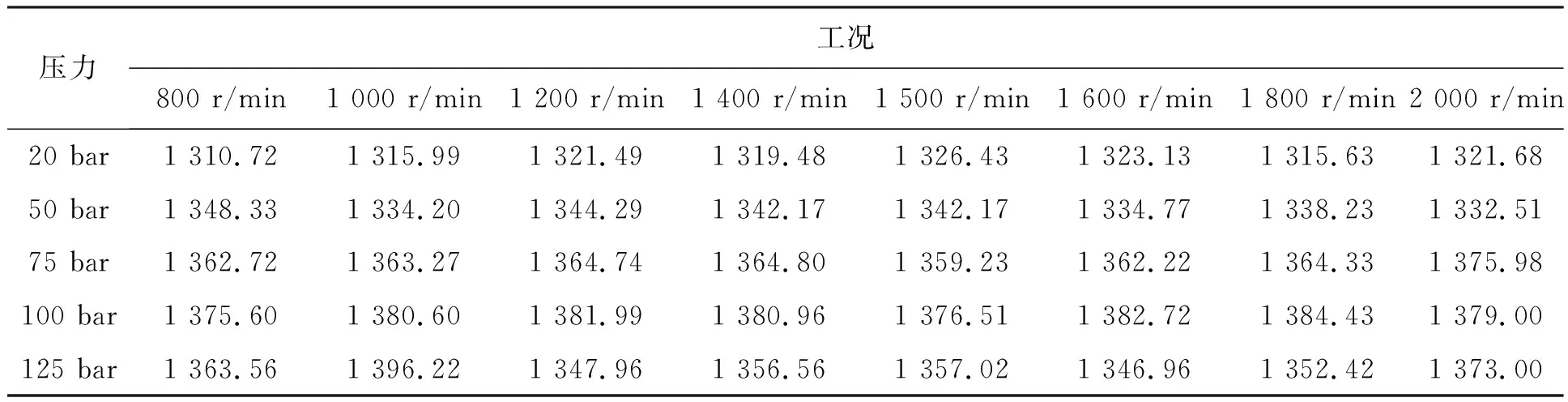
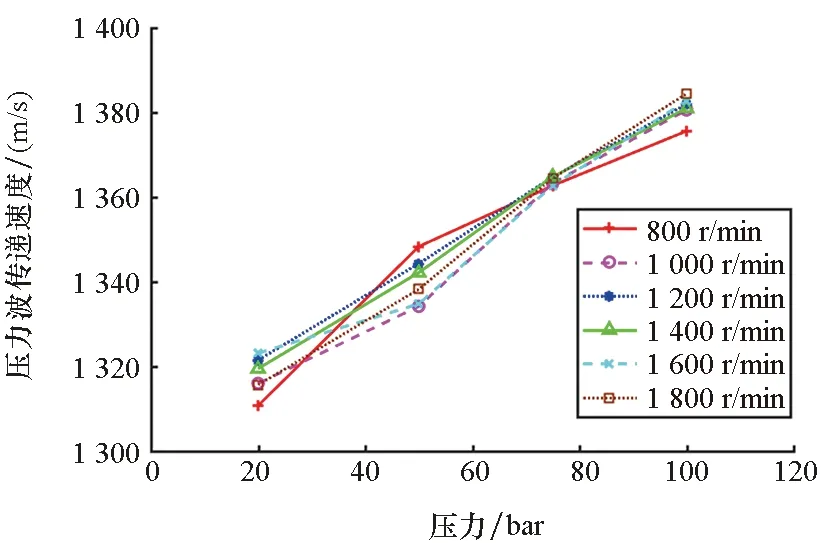
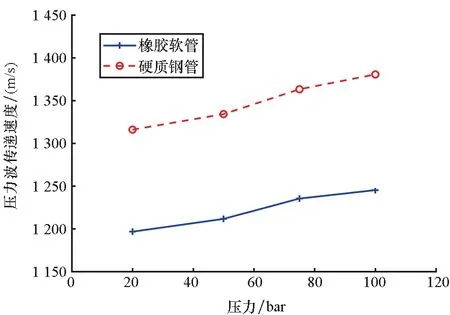
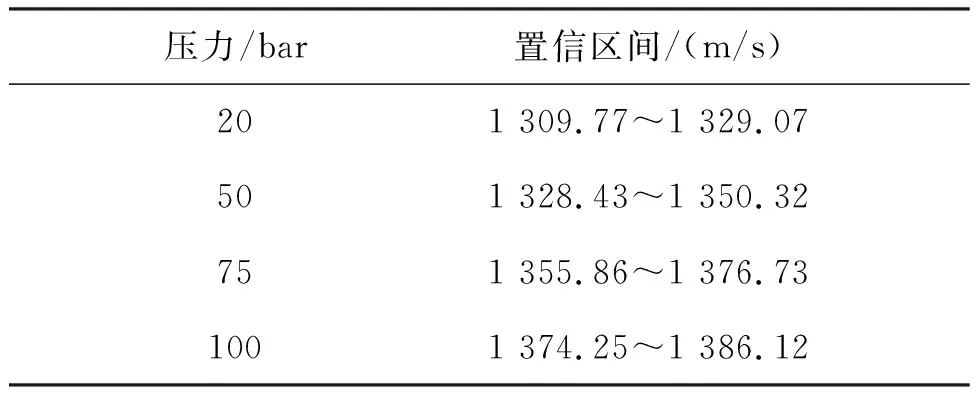
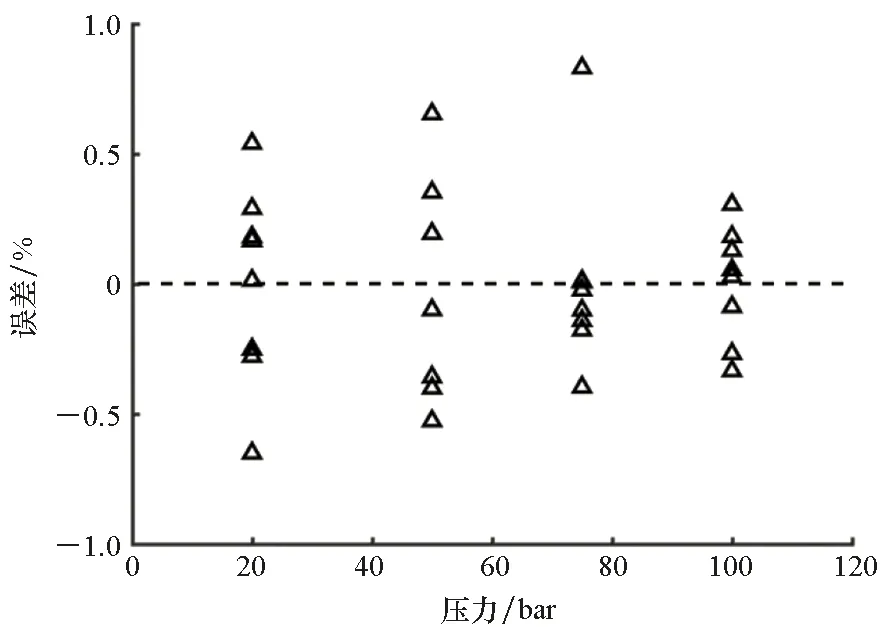
2.4 试验误差评估
3 结论

