基于JSO-VMD的滚动轴承故障特征提取方法
韩东锦 陈长征
沈阳工业大学机械工程学院 沈阳 110870
0 引言
随着工业科技不断地进步,机械设备愈发向大型化、高速化、连续化方向发展,机械设备构造越也更加复杂精细,而组成整个机械系统的重要零件也越来越多,这些设备会长时间、高强度地运行,这就会导致机械设备出现潜在故障,潜在的故障不但会造成非预计停机损失,甚至会危及人身。滚动轴承是目前使用较为普遍的机械元件之一,由于其工作环境差,且长期受到载荷等因素的影响,较易发生故障,对机械系统安全、稳定运行影响巨大,有效发现轴承故障是保证设备稳定运行的关键。
变分模态分解(VMD)是一种新型的信号自适应分解处理方法,可有效将信号分解问题转化为非递归、变分模态分解问题。因其具有良好的噪声鲁棒性,并能有效解决端点效应问题以及模态混叠问题,从而能够较好地提取出信号特征,现常用于机械振动故障信号处理中。李永琪等[1]提出一种平局包络谱峭度结合平均样本熵优化的变分模态分解方法,可以较好地对轴承故障信号进行识别。朵慕社等[2]以排列熵为指标,确定VMD分解层数,按照峭度准则,选择模态分量进行重构,利用CNN对故障进行诊断,具有较高的准确率。VMD算法中,初始参数模态分解个数k和惩罚因子α对模态分解效果有较大影响,人为设定k和α的值难以使参数组合达到最优,使分解得到良好结果。本文采用水母优化算法(JSO)自适应对VMD参数k和α进行参数寻优,以包络熵作为目标函数得到最优k和α的参数组合,经实验验证可取得较好效果。
1 变分模态分解概述
1.1 变分模态分解基本概念
变分模态分解是由Konstantin Dragomiretskiy和Dominique Zosso于2014年提出的一种信号自适应分解方法,是一种具有非递归性质的信号变分模态分解方法。在机械、卫星通讯、地质学、医学、声学等多个领域都被广泛研究与应用[3]。VMD预先假设每个由原始信号分解后的模态分量(IMF)都有一个对应的中心频率,并以此基础来确定每个IMF最优的中心频率以及带宽,由于VMD分解方法是非递归模式分解,比传统的递归模式分解有更坚实的理论基础[4]。同时,VMD分解相比于传统的自适应分解方法,有着更好的噪声鲁棒性和抗模态混叠效应以及端点效应。
VMD分解的原理是将原始振动信号通过不同中心频率[5]、有限带宽的模态函数uk进行分解。使每个IMF都有最优中心频率ωk和带宽与之匹配,故构建变分约束条件为

式中:K为VMD分解的IMF总个数,{uk}、{ωk}分别对应分解后第k个IMF和对应的中心频率,δ(t)为狄拉克函数,*代表卷积运算。
求解式(1),引入拉格朗日乘法因子λ,得到增广拉格朗日表达式,将约束变分问题转化为非约束变分问题,即有
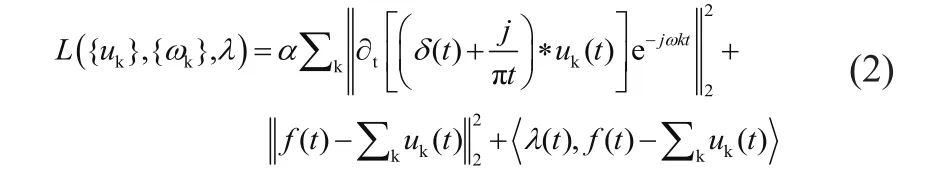
式中:α为二次惩罚项系数,目的是降低高斯噪声干扰。
利用乘数交替方向法来解决式(1)最小值问题,并使用傅里叶变换到频域,通过计算得到各IMF和对应的中心频率、搜寻增广拉格朗日函数的鞍点,交替寻优迭代后的uk,ωk和λ的表达式为

1.2 变分模态分解过程
VMD主要迭代求解过程为
2 人工水母优化算法
2.1 人工水母优化基本概念
人工水母优化算法是在2020年由Chou J S等[6]提出的仿生优化算法,该算法基于3个理想化的行为规则:
1)水母要么跟随洋流,要么在种群内围绕自身移动,且这2种运动方式由时间控制机制控制;
2)在海洋中,水母寻找食物,它们更容易被食物数量多的位置吸引;
3)找到的食物数量由该位置和对应位置的目标函数决定。
2.2 洋流运动
因为洋流中含有大量水母所需的营养物,所以水母会被吸引到洋流附近。洋流的方向由水母种群位置的平均值和水母最好位置决定。洋流方向的定义为

式中:npop为水母种群数量;X*为当前水母种群中最好的位置;ec为吸引力因子;μ为种群的平均位置;df为水母种群当前最好位置于平均位置的差分。
基于水母在所有维度服从正态分布的假设,平均位置的±βσ领域内包含所有水母的可能性,其中σ为分布的标准差,即

2.3 水母种群运动
水母种群有2种运动方式:在自身周围运动(被动运动,A型)或向其他位置运动(主动运动,B型)。当种群刚形成时,大多数水母遵循A型运动。随着时间的推移,水母越来越多地表现出B型运动。A型运动是水母围绕自身位置的运动,每个水母相应的位置更新为
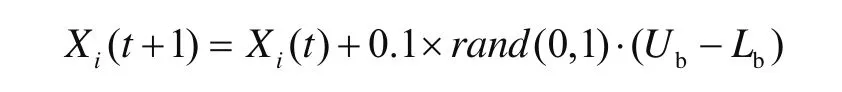
式中:Ub为搜索空间的上边界,Lb为搜索空间的下边界。
为了模拟B型运动,随机选取2个水母位置i、j来决定移动方向。当j位置的食物数量超过i位置的食物数量时,i位置的水母向j位置移动,反之远离。种群中所有的水母朝着更好的位置寻找食物。
移动方向公式为

2.4 时间控制机制
洋流中含有大量吸引水母移动的营养物质。随着时间的推移,更多的水母聚集在洋流中形成水母群。当温度或风改变洋流时,种群中的水母进入另一个洋流,形成新的水母群。种群内的水母表现出A型和B型运动的切换。当水母群初形成时,更多的水母服从A型运动,但随着时间的推移,B型运动越来越受到欢迎。
本文引入时间控制机制来模拟这种情况。为了调节水母在洋流中和水母种群内运动,时间控制机制使用时间控制函数c(t)和恒定阈值c0。时间控制函数是随时间而变化的随机值,范围是0~1。下式制定时间控制函数,当它的值超过c0时,水母跟随洋流运动。当它的值低于c0时,它们会在水母种群内运动。c0的值不能完全确定,时间控制函数的值域范围为0~1。因此,c0被设置为0.5,即0和1的平均值。
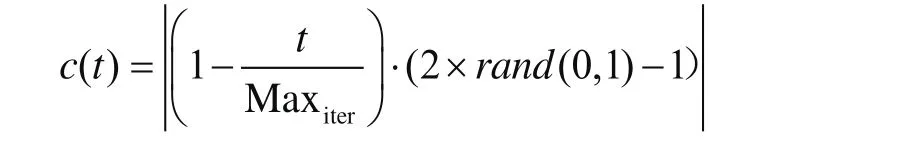
式中:t为指定迭代数,Maxiter为最大迭代数,是一个初始参数。
c(t)与一样,1-c(t)用于描述水母运动类型(A型或B型)。当0.5大于1-c(t),水母遵循A型运动。当0.5小于1-c(t),水母遵循B型运动。随着时间从0向1的推移,0.5>1-c(t)的概率逐渐变低,水母在种群内的运动越来越趋向于A型运动。
2.5 边界处理
设置水母游动位置的边界,当水母移动超出搜索边界,将会向边界相反的方向移动,即有

式中:Xi,d是第i个水母位置的d维分量。
2.6 种群初始化
水母种群初始位置通常都是随机的,采用随机初始化的种群容易出现收敛速度缓慢、不能跳出局部最优解以及种群多样性较低的缺陷。为了提高初始化种群多样性,许多混沌映射被开发。如Logistic map、Tent map、Liebovitch map等。其中,Logistic映射是一种结构较为简单的混沌映射。这种初始化的种群比随机初始化种群更具有多样性。映射公式为

式中:Xi是第i个水母位置的逻辑混沌映射值;X0用于产生初始种群,X0∈(0,1),X0∉(0,0.25,0.5,0.75,1.0),η=0.4。
2.7 水母优化流程
1)初始化种群;2)计算当前位置,确定目前水母最优位置X*;3)当前迭代次数是否小于最大迭代次数,如果是即进行下一步,否则迭代终止并输出当前水母最优位置为全局最优位置;4)运用时间控制函数,当c(t)大于0.5时,执行洋流运动并更新位置,跳转到步骤6),否则进入步骤5);5)判断并执行水母种群内运动(A型或B型),并更新位置;6)检查边界,计算并更新当前最佳位置X*,迭代次数加以并返回步骤3)。
3 实例分析
实验数据采用美国Case Western Reserve University的轴承故障数据,该数据是当前公认较权威的一组故障分析数据[7],其广泛应用于轴承故障诊断领域。该平台由一个1.5 kW的电动机、扭矩传感器和电子控制器组成。实验的对象采用实验台驱动端的轴承,型号为SKF6205,轴承的故障损伤点是用电火花加工的单点损伤,损伤直径为0.1778 mm,信号采样频率为12 kHz,采样点数为4 096,电动机转速近似为1 797 r/min,根据轴承参数、转子转速和轴承内圈故障特征频率计算公式,通过计算得到轴承内圈故障特征频率为161 Hz。
使用JSO算法优化VMD参数,寻优迭代曲线如图1所示,最优参数组合如表1所示。

表1 JSO参数优化VMD参数

图1 JSO优化迭代曲线
将通过JSO算法得到的最优参数代入到VMD分解方法中,各分量时域图如图2所示,各分量的峭度值如表2所示。

表2 各IMF模态分量峭度值
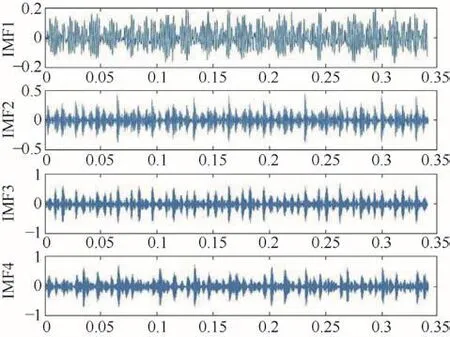
图2 各分量时域图
由表2可知IMF4的峭度值最大,故障冲击特征最明显,对IMF4进行包络分析,结果如图3所示。图中频率最大峰值为161.13 Hz,与通过计算所得的轴承内圈理论故障频率161 Hz非常接近,由于存在测量、计算等误差的影响,理论故障频率与实际IMF分量包络分析得到的故障频率特征存在一定误差,由于误差微小,且故障特征频率处峰值明显,可见JSO-VMD成功提取了轴承内圈故障特征。

图3 IMF4分量包络图
4 结论
由对实际轴承内圈故障的故障诊断,经过JSO算法,实现VMD算法当中参数K和惩罚项系数的自适应取值。利用JSO-VMD方法对轴承内圈故障信号进行分解,通过计算各IMF的峭度值,选择峭度最大的IMF作为敏感分量。对敏感分量进行包络分析,通过对包络谱的分析,可明显得出故障特征,与通过计算得到的理论故障特征频率进行比对,故障特征频率极为相近,忽略误差的影响,证明了该方法有着较好的故障诊断能力和效果。

