基于复合度量的联合表示高光谱图像分类

刘庚才，赵红举 ，黄 湮，邱文豪，陈 湘

(湖北科技学院 数学与统计学院，湖北 咸宁 437100)

高光谱遥感(hyperspectral remote sensing)兴起于20世纪80年代，是在成像光谱学(imaging spectroscopy)的基础上发展起来的一种全新遥感技术[1]。借助高精度的机载或星载成像光谱仪，在记录地物的二维平面位置信息的同时可采集地物反射或发射的电磁波存储在第三维。现今的成像光谱仪，能在波长间隔达到10nm、波段数超过100个的分辨率下，从可见光至近红外区域，对像元产生一条完整而几乎连续的电磁波谱特征曲线。不同的地物表现出不同的光谱特征，其波谱反射曲线特征存在差异性，对高光谱数据特征的解译，为基于高光谱图像(hyperspectral image, HSI)的分类、分割和目标检测等应用提供了可能。

高光谱数据光谱通道的高维特性，提高了其应用广泛性的同时也给数据的后期处理提出了挑战。如在分类问题中，数据的高维特性所导致的“维数灾难”问题(Hughes现象)。为有效挖掘光谱通道中蕴含的有判别作用的特征，科研人员开发出众多的分类模型，比如非参数分类器和参数分类器。k近邻分类是可应用于高光谱图像分类的一种经典的分类方法[2]，属于一种非参数的分类器。而诸如最大似然估计模型、高斯混合模型[3]得到的分类器则属于参数型分类器。

近十来年，发端于人脸识别领域的稀疏表示(sparse representation, SR)理论[4]引发了研究人员的大量关注。从信号表示的角度看，就是信号可以表示成字典原子(训练集中的样本)的线性组合，稀疏表示意味着信号可以被字典中同一类别的少数原子的线性组合表示。这样，字典中不参与表示的字典原子在线性表示时的系数为零，此时得到的大多数分量为零的表示向量称为稀疏的。后来，Zhang等提出了协同表示(collaborative representation, CR)分类[5]。这是一种基于最小二乘框架设计的分类器，但将稀疏表示中的L0正则化替换成L2正则化，该分类器将测试样本直接表示为全类别样本的线性组合。实验表明，协同表示分类器不仅取得了与稀疏表示同样的分类精度，而且由于存在解析解，可使表示向量的求解更快。

稀疏表示或协同表示的策略也被研究人员应用于高光谱图像分类问题[6-7],更多经改进的模型也陆续被提出。如Li等提出的最近正则子空间分类器(NRS)[8]，通过对正则化项的进一步优化，文章的方法改进了表示分类器的性能。结合像元的空间关联性，联合稀疏表示(JSR)[9]或联合协同表示(JCR)[10]分类模型则明显提升了仅采用光谱的表示分类器的性能。事实上，高光谱图像的像元对应的地物在地面分布上存在某种连续性，所以目标像元与其周边一定范围的像元存在一定的同质性，因而它们的光谱有着一定概率的相似性。所以，不管是将一定邻域范围内的光谱特征综合到单个目标像元上，再对该像元作表示，还是将目标像元及其邻域整体作表示来判定目标像元的类别，都可以使待测像元的光谱特征得到加强，提高类别的区分度。

鉴于在样本量不是很大的时候，k最近邻可以以非常简单、快捷的方式搜索到与目标样本相近的同类样本，这一算法可用于表示分类模型过完备训练字典的筛选。光谱信息与空间信息的结合，实实在在地提高了协同表示模型在面向高光谱图像分类时的性能。本文将复合的光谱相似性度量用于测试样本的个性化字典的构建，再结合非一致性正则化的协同表示模型，针对光谱信息与空间信息融合后的高光谱图给出了一种分类算法。文章第一节给出了一些背景和预备知识，第二节给出了分类算法及其过程，第三节则在通行的数据集上开展了算法实验并分析了实验的结果。最后，第四节对全文进行了总结。

一、预备知识

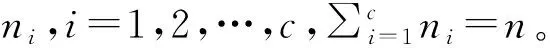
1.光谱相似性度量与k最近邻算法

在对光谱数据进行解译时，通常要对光谱的相似性进行度量。以对两个光谱的相似性度量为例，依托某个特定的光谱相似性度量函数ρ(·，·)：Rd×Rd→R，判定待测光谱y(类别未知)与参考光谱x(类别已知)之间的相似程度，并根据ρ(y,x)的大小执行相应的操作，如字典原子的选择、测试样本类别的标记等。高光谱数据分析的几个主要研究领域，如异常目标检测、地物分类、混合像元分解等，均以光谱相似性度量为基础[11]。目前主流的对两个光谱相似性度量的方法可归纳为如下四种：基于距离的光谱相似性度量、基于投影的光谱相似性度量、基于信息散度的光谱相似性度量、基于统计特征的光谱相似性度量。

光谱的幅值决定向量在空间的长度，欧氏距离与其幅值的大小直接相关，反映了几何空间中两个点的真实距离，它对光谱的形状差异不敏感，距离度量小的两个光谱可能形状差异比较大。基于投影的光谱相似性度量则可在一定程度上反映出光谱的形状差异。在光谱向量空间中，光谱的形状表现为光谱在空间中的方向，两个光谱的形状特征差异表现为它们夹角的大小。Kruse等[12]提出计算两个光谱向量的夹角大小来评价光谱的相似度，夹角越小两个光谱相似度越高，反之越低。设xi,xj是两个d维的光谱向量，则光谱夹角的计算公式为：

dθ(xi,xj)称为光谱向量xi,xj的光谱角度量(spectral angle metric，SAM)。显然，光谱角度量具有倍乘不变性，即dθ(αxi,βxj)=dθ(xi,xj),0<α,β≤1。这说明在欧氏空间中，光谱幅值的变化不影响夹角的大小，所以光谱角度量对光谱的形状差异要比对光谱幅值的变化敏感。这使得光谱角度量能克服因复杂地形、光照强度和阴影变化等因素对光谱幅值的改变，弥补了光谱幅值利用的不足。光谱角度量方法被广泛应用于光谱角填图(spectral angle mapping，SAM)研究，在地物分类和岩性识别都有很好的应用。研究人员还在光谱角度量的基础之上提出了光谱梯度角度量，以及核空间的光谱角填图[11]。

k最近邻算法是早期分类算法中非常简便的一种监督学习方法。kNN分类实际上并没有创建一个抽象模型，无需花费时间做模型的构建，属于一种懒惰算法，其在训练时间上的耗费基本为零。但它在测试样本分类时的计算量大，内存开销大。kNN算法的优点是明显的，它易于理解，易于实现，无需估计参数，特别适合于多分类问题。对于类域的交叉或重叠较多的待分样本集来说，kNN方法较很多方法更为适合。

kNN方法的参数k一般采用交叉检验来确定，取值一般低于训练样本数的平方根，并且取k=1常常会得到比其他值好的结果。不过，在样本充足的情况下，选择较大的k值能提高抗噪性能。kNN通常用欧氏距离作为度量，前文提到的SAM也可作为选择最近邻的度量。改变度量方式可能使选中的待测样本的最近邻显著不同，会导致分类结果产生较大改变。对于类域的交叉或重叠较多的样本集来说，比如高光谱数据集，kNN方法是不错的选择，它可以帮助对训练集做初筛，找到与待测光谱更相似的光谱充当表示原子。

2.表示分类模型

研究高光谱图像分类时，通常假定同一类的光谱分布在同一维度的子空间中。假如测试样本y∈Rd来自第i 类，稀疏表示分类(SRC)则认为y可以在第i类训练样本的张成空间近似作线性表示，即

y≈αi,1xi,1+αi,2xi,2+…+αi,nixi,ni=[xi,1xi,2…xini][αi,1,αi,2,…，αi,ni]T=Xiαi，其中αi是选用第i类样本表示时的系数向量。实际上，y的类别标签是未知的，这样y需要在全部训练样本X的张成上表成线性组合y=Xα,α=[α1;α2;…；αc]，是对应全部训练样本的n维列系数向量。理想情形下，一个属于第i类的测试样本的表示系数，除了第i类系数之外的都应该等于零，此时y在X上的表示是稀疏的。

不同于在整个训练集上的协同表示，Li等提出了逐一在子空间中进行协同表示的最近正则子空间分类(NRS)方法，该分类器每次仅在一类训练样本上寻求y的线性表示，并采用关联距离度量的非一致正则化项。NRS既能实现CRC的计算优势，也能体现同类样本对测试样本的差异化惩罚，改善了上述SRC和CRC对表示系数的惩罚一致性不足。

NRS求解表示系数的算法模型如下，

3.“光谱-空间”联合策略

地物分布通常具有一定的连续性，也就是说，目标地物与其周边一定范围内的地物具有较高概率的同质性。对高光谱图像而言，平面上的某一像元与其几何距离相近的周边像元的光谱会比较相似，它们属于同一类别的可能性大。故而，在高光谱图像分类中采用“光谱-空间”相结合的分类方法可以比仅利用光谱特征的分类方法取得更好的分类结果，因为前者不仅利用光谱特征，也结合了来自空域的信息。光谱特征与空间信息融合分类一经提出，其对分类器性能的提升立刻引发了大量关注，成为近几年的研究热点。

在表示分类模型中融入空间信息同样显著提高了模型的分类性能。如在文[10]提出的稀疏表示模型中，以待测像元为中心，将其正方形邻域中的全部像元光谱取平均作为待测像元新的光谱，之后对中心像元进行稀疏表示。另如文[9]，将待测像元及其正方形邻域内的全部像元当成一个像素块，再对这个像块进行稀疏表示。这两种方法都渗透了“光谱-空间”联合分类的思想，但在融入空间信息的策略上有所区别。前者将邻域的光谱特征信息集中到中心像元上，使得中心像元的光谱特征得到加强，增强了其光谱特征的辨识度，后续过程处理的是单像元。后者将局部邻域的光谱连续性作为考察的重点，后续过程处理的是像素块这一整体。这两种策略都只利用了邻域像素的光谱特征，并未利用邻域像素的标签信息。

另外，邻域的大小，即所选窗口的半径直接影响所提供空域信息的像元数目的多少和质量的高低。邻域选择过大可能导致过多的异质像元参与，提供的光谱信息过于混杂，对后续的分类产生不利后果。邻域选择过小会使得空间信息利用不充分，不能充分发挥“光谱-空间”联合策略的优势。邻域范围的选择有固定方式和自适应方式，前者对所有测试样本都选择同一邻域尺寸来获取空间信息，后者对不同测试样本会自适应地选择邻域尺寸获得空间信息[13]。

二、基于复合度量的联合表示分类器

考虑到在高光谱图像分类问题中，提供的训练集常具有一定的冗余度，将训练样本筛选后进行分类可以改善相关模型的分类性能。本节把基于距离和基于投影的光谱相似性复合度量作为kNN算法中最近邻选择的度量，生成低冗余度的字典，结合常用的“光谱-空间”联合策略，在表示分类模型的框架下，综合了CRC和NRS的优势，提出了一种改进后的表示分类器，称为“基于复合度量的联合表示分类器(CJR)”。

1.复合度量

为弥补光谱距离度量和光谱角度量在衡量光谱相似度上的不足，采用一种“复合度量”来衡量像元之间的相似性。这种方法综合考虑两个比较像元的光谱距离和光谱夹角，是一种既对光谱的幅值敏感，也对光谱的形状敏感的度量方式。该复合度量dC(x,y)表示为，dC(x,y)=(1-cos(dθ(x,y))×dE(x,y),dθ(xi,y)即前文给出的光谱角相似度量，dE(x,y)即常见的欧氏距离度量。容易验证，复合度量dC(x,y)满足“距离度量”的基本性质中的“非负性、同一性、对称性”，但不满足“直递性”，即不能保证不等式dC(x,y)≤dC(x,z)+dC(z,y)一定成立。

通常，我们一般基于某种形式的距离来定义“相似度度量”，且参照距离越大相似性越小的原则进行评价。然而，用于相似度度量的距离未必一定满足距离度量的所有基本性质，尤其是直递性[14]。在一些实际分类任务中所建立的相似度度量不满足直递性有其合理的考虑，直递性不成立并不一定会产生决定性的影响。

此处针对高光谱图像分类设计的复合度量，乘式中的前项发挥了光谱角度量相似性的长处，降低了复杂地形中地物的错误分类，后项则发挥了在处理平坦区域中的地物光谱的优势，因为此时地形的影响降低，光谱亮度值成为地物区分的重要参考特征。将特定的相似度进行复合，可以增强像元的细节信息，提高彼此的区分度。

2.分类器算法流程

分类器算法可按以下五步实现。

三、实验与分析

选用高光谱图像处理中常用的帕维亚大学(Pavia University)数据集[ http://www.ehu.eus/ccwintco/index.php/Hyperspectral_Remote_Sensing_Scenes#Pavia_University_scene]进行分类实验。本节给出了基于欧氏距离度量的kNN(Ed-kNN)方法，基于光谱角度量的kNN(An-kNN)方法，基于复合度量的kNN(Cm-kNN)方法等三种kNN分类器和联合协同表示(JCR)分类器、复合度量的联合表示(CJR)分类器等两种表示型分类器的分类结果及分析。实验借助安装在个人电脑的科学计算软件MATLAB 8.3进行。

1.数据集与评价指标

帕维亚大学数据集：数据由德国的机载ROSIS成像光谱仪于2003年采自意大利帕维亚市的Pavia University。 图像地面分辨率为1.3m，经裁切后保留610×340个像元，像元原有115个波段(波长范围0.43-0.86)，分类前去除了12个水吸收和噪声波段，共有9个地面物类，每类的样本数见表1。

表1 帕维亚大学数据集类别和样本数

对分类器性能的衡量，选取了总体准确率(OA)、类准确率(CA)、平均准确率(AA)、卡帕系数和分类时间(秒)等五个指标进行比较。

2.实验结果分析

实验按每类随机选取60个样本组成540个样本的训练集，各类剩余样本用于测试。实验随机进行了5次，然后计算5次的平均值得到数据，见表2。表2后五列各给出了一个分类器的分类数据统计，另外，还通过图1—图3给出了相关参数的变化对分类器的总体准确率影响的对比。其中三个最近邻型分类器的参数k、表示分类器的正方形邻域参数w和正则化参数λ均由人工多次试验，对比结果后选定。

表2 帕维亚大学数据集五个分类器的结果(%)对比

表2明显可见，两个表示型分类器在指标OA、AA和Kappa要明显优于三个最近邻分类器。在单类的准确率上，除了在第9类上表示型分类器逊色于三个最近邻分类器，第5类两个类型分类器效果相差无几外，其它七个类都是表示型分类器JCR和CJR占据较大优势，尤其是第6、8两个类别。在时间消耗方面，表示算法因为需要计算大量训练样本的表示系数，所以分类时间达到了最近邻分类器的近10倍，这是提高准确率不得不增加的计算成本。对比CJR和JCR的OA/AA/Kappa值和Time值，发现CJR用相当于JCR 42.8%的时间成本就已达到JCR同样的OA/AA/Kappa值，这说明在表示分类的机理下，训练字典的确存在冗余性，这为表示字典的筛选和改进提供了可研究的空间。

Ed-kNN、An-kNN和Cm-kNN三个分类器都需用到最近邻参数k，图1比较了这三个基于不同相似性度量的最近邻分类器的OA值依参数k的走势。首先，图1显示，在帕维亚大学数据集上，参数k=2时，三个最近邻分类器都取得最大OA值，之后随k值增大而减小，这验证了前文所述多分类问题中一般取较小的k值kNN效果会比较好。另外，1

图1 Ed-kNN/An-kNN/Cm-kNN的k值对OA值的影响对比

最近邻参数k对基于复合度量从原始训练集中选择字典原子的CJR分类器的效果产生影响，图2给出了Cm-kNN与CJR的OA值依最近邻参数k的变化趋势。首先，CJR分类器不同于Cm-kNN的是，k值的增大提升了表示分类器的OA值，而不是像Cm-kNN那样是减小的。显然，最近邻参数k的增大，意味着表示字典的原子数目更多，字典的表示能力相应会增强，故如图中曲线可见，k值的增大让CJR分类器的OA值一直在递增。但Cm-kNN中较大的k值会使kNN型的分类器的最近邻数目增多，会改变最近邻中各类别的比例，导致错误的类别投票结果。从图中CJR分类的OA值的增长曲线看出，k值增长对它的OA提升作用边际效果递减，后期非常缓慢，基本呈停滞状态。这与k值对Cm-kNN的OA值的影响是截然不同的。因为k增大使字典原子达到一定量后，大量有效的字典原子已基本被最近邻原则搜索到，再次增加原子数起到的作用不明显。假如k增大到原训练样本数540，其效果就等同于JCR分类，这时最近邻对字典原子的选择作用已经丧失，还徒增了对原子的排序计算消耗。所以对CJR来说，对其参数k的选择要综合考虑OA提升所付出的计算代价，无限制增大k值肯定是不可取的，表2的CJR分类结果是在k=60时获得的。

图2 Cm-kNN和CJR的k值对OA值的影响对比

图3 JCR和CJR的邻域参数值w对OA值的影响对比

四、总结

在高光谱图像的协同表示分类器中，训练集常有一定的冗余度，直接将全部训练样本用作字典，会产生一些不必要的时间消耗。故将训练样本筛选后重建表示字典，可改善分类器的分类性能。采用“光谱-空间”联合的策略对初始像元进行加工得到的像元空间信息更丰富，考虑到光谱的物理特性和几何特征，将两者融合得到的复合相似性度量具有互补性，采用该度量作为k近邻算法的距离选择标准，能构建更简洁的训练字典。在非一致性正则化协同表示的模型框架下，本文的基于复合度量的联合表示分类器，其精度对比一般的协同表示分类器不分伯仲，但时间耗费上更为节省。所以，该分类器提升了常规的欧氏距离度量或光谱角度量表示分类器的综合性能。