应用独立成分分析和小波分解对木材声发射信号的析取1)

罗蕊寒 方赛银 丁锐 赖菲 王明华 李晓崧 罗廷芳 李明

(西南林业大学，昆明，650224)(安徽工程大学)

材料在外力或内力作用下，以弹性波形式释放出应变能的现象称为声发射(AE)[1]。工程上，用仪器探测、记录、分析声发射信号和利用声发射信号推断声发射源信息的技术称为声发射技术(AET)[2]。声发射技术，不仅可以动态监测材料内部及表面的应力变化，还可以通过声发射源定位技术确定损伤位置[3-4]。声发射信号本质上是一种非平稳随机信号，在应力释放不是特别集中时，声发射信号容易被噪声覆盖。这种情况下，如何有效地将声发射信号从噪声中析取出来并加以分析，是应用声发射技术的关键问题之一。在木质材料无损检测领域，相关研究[5-10]已经证实了在信噪比较高的情况下，小波和小波包分析是一种非常有效的信号析取方法；但是，对于从被噪声覆盖的混合信号中提取声发射信号，小波分析法具有显著的局限性。

依据信号统计特性的独立成分分析(ICA)，对于线性混合信号的信噪分离具有显著的优越性。独立成分分析的信号处理方法，在机械工业、医疗等领域已有应用[11-13]，但在木材工业领域的应用并不多见。

木质材料在发生实质性损伤时，收集的声发射信号往往是多个损伤声发射源和噪声随机混合的结果，可以认定为是一种复杂线性混合信号。若将混合信号进行分离，将噪声和声发射源所产生的独立信号分离开，再对其进行分析，便会使木材状态监测的准确度显著提升。为此，本研究针对被噪声覆盖的声发射信号析取问题，提出一种快速独立成分分析和小波分解(FastICA-Wavelet)的声发射信号析取方法。选取常温气干状态表面无缺陷的樟子松(Pinussylvestrisvar.mongolicaLitv.)实木为试验材料，使用UTM5105型万能力学试验机对试件进行破坏性试验，以500 kHz的采样频率采集木材三点弯曲试验产生的声发射信号，截取试验后期幅值无显著变化的一段原始信号作为研究对象。采用依据负熵最大化的快速独立成分分析(FastICA)盲源分离算法将原始信号分离成噪声和声发射信号，再对分离后的声发射信号进行5层小波分解后重构声发射信号波形；对重构声发射信号进行频域分析，通过与已知声发射信号的频域特征比较，验证信号析取的有效性。本研究结果可为以后木材损伤的声发射信号的降噪、多声发射源信号盲源分离以及其它材料的损伤声发射信号的分离提供参考。

1 材料和方法

1.1 材料及试验设计

选常温气干状态表面无缺陷的樟子松(Pinussylvestrisvar.mongolicaLitv.)实木作为试验材料，制成长800 mm、宽60 mm、厚30 mm的试件，使用UTM5105型万能力学试验机(最大试验力100 kN、功率1.5 kW)对试件进行破坏性试验。应用NI USB-6366高速采集卡和LabVIEW软件自行搭建声发射信号采集平台；其中传感器型号为SR150N，带宽为22～220 kHz，PAI声发射前置放大器的增益为40 dB，采集卡最高采样频率为2 MHz。已有研究表明，木材声发射信号最大频率约为200 kHz[13-14]，根据香农采样定理，为了不失真地恢复模拟信号，各通道的采样频率设置为500 kHz。

采用三点弯曲的方式对樟子松试件进行横向加压，设置的跨距为200 mm，并设定1 mm/min的速度对木材进行匀速加载。在木材试件对称轴的两侧对称放置2个传感器，传感器间的距离设定为300 mm(见图1)，将硅脂作为耦合剂涂在传感器和木材的接触面之间，保证采集的信号更为准确。对樟子松试件持续加载，直到试件宏观断裂之后卸载，以确保获得试件从弹塑性变形到宏观断裂所有过程的原始信号。

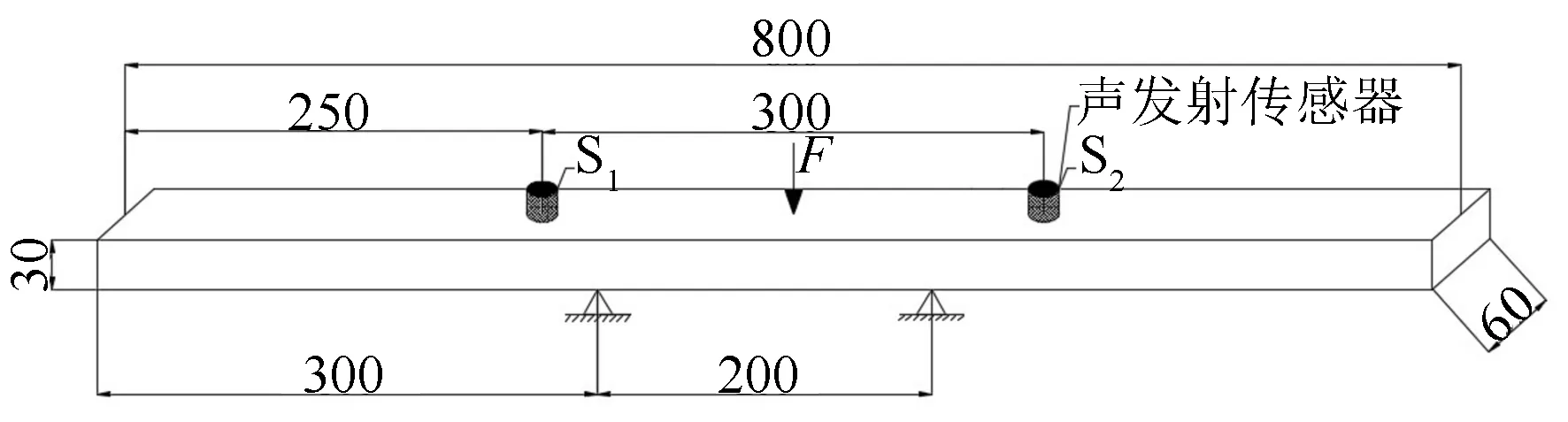
图中数据单位为mm

1.2 独立成分分析算法

1.2.1 算法原理

独立成分分析算法，是指在源信号与线性变换都未知情况下，仅通过观测信号估计源信号的一种信号处理方法。

设n个传感器采集到的n个观察信号为X(t)=[x1(t)，x2(t)，…，xn(t)]T，得到的每个观测信号所包含的m个未知源信号为S(t)=[s1(t)，s2(t)，…，sn(t)]T；A为一个未知的n×m的混合矩阵(n≥m)，观测信号便可表示为X(t)=A·S(t)。由于源信号(S(t))和混合矩阵(A)都是未知，已知因素只有传感器采集的信号(X(t))，所以独立成分分析的目的，是使用一个分离矩阵(W)把互相独立的源信号从混合信号中分离出来，即分离信号(Z(t))可表示为Z(t)=W·X(t)。独立成分分析的算法流程见图2。

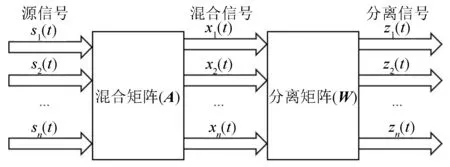
图2 独立成分分析算法流程示意图

1.2.2 负熵

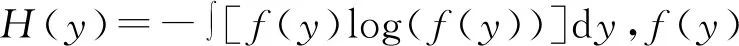
在信息论中有个基本的结论：在所有方差均相等的随机变量中，高斯变量的熵最大，表明高斯分布是所有分布中最“随机”的。为了获得对于高斯变量时为零，并且总是非负的非高斯性度量，通常使用负熵(J)。负熵的定义为J(y)=H(yg)-H(y)，yg为与y有相同协方差矩阵的高斯随机变量。

由负熵的特性可知，负熵一直是非负数，只有y是高斯变量的时候负熵才为0。但是，由于在实际研究中，无法知道该变量的概率密度函数，负熵的计算便会非常困难，所以在实际应用中会使用负熵的近似，即JG(y)≈{E[G(y)]-E[G(yg)]}2，G为可选择不同类型的非线性函数，选择增长不是太快的非线性函数(G)，会得到一个比较稳定的估计量。

对于统计性质而言，负熵在某种意义上是对非高斯性的最优估计。所以本研究采用的算法是快速独立成分分析，是依据负熵最大化理论的独立成分分析算法。

2 结果与分析

文献[16]研究表明，木材受损过程中会产生两种不同的声发射信号，分别为以低频为主的变形声发射(DAE)信号、以高频为主的断裂声发射(FAE)信号[16]。在木材弹塑性变形后期阶段(即将宏观断裂之前)，此时声发射信号丰富、幅值低、易被噪声覆盖，但是此时会产生以断裂声发射信号为主要成分的损伤信号，具有较高的辨识度；所以，本研究试验采用试件弹塑性变形后期阶段的信号作为研究对象。对试件进行三点弯曲试验，试件在340 s时发生宏观断裂，所以截取试件宏观断裂之前的4 000个数据长度的原始信号作为研究对象，即宏观断裂前的8 ms内的原始信号(见图3)。

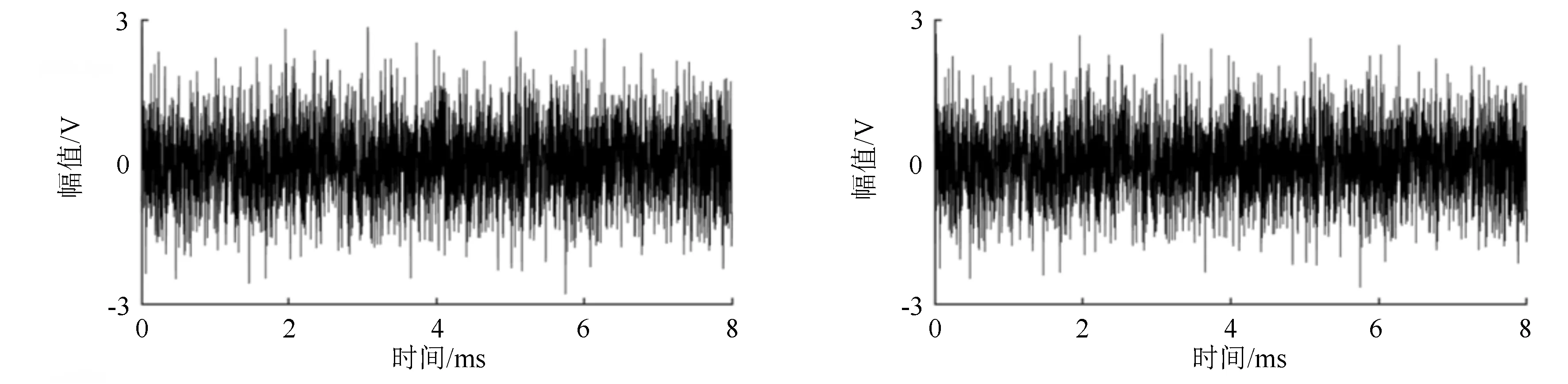
(a)传感器S1采集的木材声发射原始信号 (b)传感器S2采集的木材声发射原始信号

由图3可见：2个原始信号很像1个典型的噪声信号，无法直观地看出声发射信号的波形。尝试对2个传感器的原始信号使用传统小波处理的方法进行5层分解，并寻找具有声发射信号特征的细节信号，以达到对原始信号进行降噪并析取声发射信号的目的。由于2个通道原始信号经过小波分解之后，其5层细节信号都无法看到明显的声发射信号特征，故选用对传感器S1采集到的信号进行小波分解的结果(见图4)加以说明。

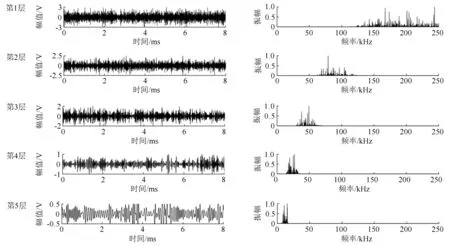
图4 传感器S1采集的木材声发射信号小波分解细节信号时频域图

由图4可见：从第1层到第5层的细节信号都无法看出明显的声发射信号的波形，并且从高频段到低频段相应的频率分布不集中，进而无法选出包含具有声发射信号特征的细节信号进行重构。试验表明，小波分解在低信噪比的情况下降噪能力不理想，并且无法对声发射信号进行析取。

因为小波分析的方法，是通过小波基在信号时间轴上进行平移和伸缩对该信号进行分析，可见小波分析的方法是极度依赖信号时域部分。而在低信噪比的情况下，需要析取的声发射信号被噪声覆盖，在时域上噪声占主要成分，小波分解出的细节信号中也以噪声为主要成分，此时再使用小波的方法很难对占比较低的声发射信号进行析取。

独立成分分析是依据统计原理的算法。虽然在低信噪比的情况下噪声占主要成分，但是噪声的随机性一定远大于声发射信号的随机性。由J(y)=H(yg)-H(y)可知，声发射信号的负熵会远大于噪声的负熵，便可根据最大非高斯性的方法将噪声和声发射信号分离开，实现信噪盲源分离；所以，本研究使用的是依据负熵最大化的快速独立成分分析算法。因为本研究以析取声发射信号为目的，只考虑声发射信号的时域波形和相应频谱，并不涉及信号的能量水平，在独立成分分析分离过程中，原始信号与分离信号的能量关系会丢失[17]，所以对输出的分离信号的幅值进行规范化处理，便于看出2个信号时域图的区别(见图5)。

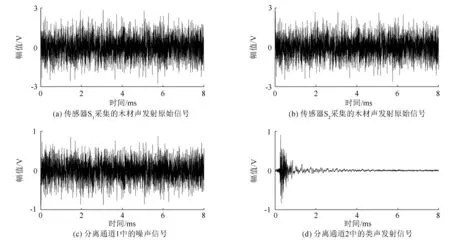
图5 木材声发射原始信号和分离信号时域图

通过快速独立成分分析处理之后，得到2个区分度很大的分离信号。分离通道1的分离信号时域图(见图5(c))，其对应频谱见图6(a)；由图6(a)可见：，该信号在0～250 kHz范围内均有明显的成分，并且分布不集中，所以认定分离通道1的分离信号是个典型的噪声信号。分离通道2的分离信号(见图5(d))，其对应频谱见图6(b)；由图6(b)可见：该信号的波形与试验所需析取的声发射信号极其相似，但是它的主频在低频，不属于断裂声发射信号，并且它的低频集中在4.0 kHz和13.1 kHz，在传感器的带宽范围之外，所以认定分离出的类声发射信号中仍存在低频噪声，影响声发射信号类型辨识。快速独立成分分析可以将声发射信号与互相独立的环境噪声分离开，但是无法分离在声发射信号发生和采集过程中的不独立噪声，这些噪声因素会影响声发射信号的频谱分析；此时分离信号的主要成分是声发射信号，便可使用传统的小波方法对其进行降噪。使用文献[7]的小波分析法，对分离出的类声发射信号进行高通滤波之后再进行5层小波分解，并选取第2层和第3层进行重构，进一步降低低频噪声和高频噪声对真实声发射信号频域特征的影响，最终再对重构后的信号进行频谱分析(见图7)。

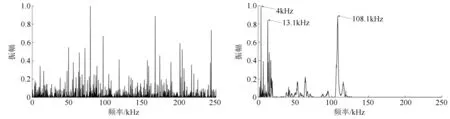
(a)分离出的噪声信号频谱图 (b)分理处的类声发射信号频谱图

从时域图(见图7a)可见，经过小波分解和重构后的声发射信号噪声成分明显减少；并且在频域图(见图7b)可见，主频分布在108.1 kHz；可以判断它是主频为高频的断裂声发射信号，符合木材弹塑性变形后期阶段产生主要成分为断裂声发射信号的结果。证明独立成分分析和小波分解的声发射信号析取方法，可把试件弹塑性变形后期阶段被噪声覆盖的断裂声发射信号分离出来。

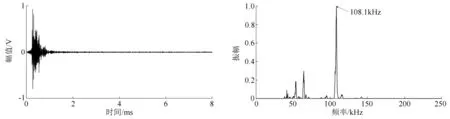
(a)小波重构后的声发射信号时域图 (b)小波重构后的声发射信号频域图

小波分解和重构的方法在信噪比较低的情况下析取效果急剧下降，但独立成分分析和小波分解的声发射信号析取方法，在低信噪比的情况下仍具有稳定的析取效果。虽然传统的小波分解和重构的方法对强噪下的声发射信号的析取具有局限性，但是它可以弥补快速独立成分分析算法无法对分离出的声发射信号完全去噪的缺陷。

3 结论与讨论

传统声发射技术都是对木材损伤产生的信噪比较高的声发射信号进行分析的，所以很少存在声发射信号被噪声完全覆盖的情况，便可以直接使用小波分解并重构使声发射信号特征成分最大化，噪声成分最小化，再对信号特征进行分析，从而得到木材的损伤状态。在实践中，经常会出现在低幅值声发射信号水平下，噪声将声发射信号完全覆盖，小波分解和重构的传统处理方法会出现局限性，无法析取声发射信号，便失去了对木材损伤特征进行分析的基础，无法对木材的状态进行监测。

对于此种情况，需要一种依据独立成分分析的信噪分离方法，所以本研究使用依据负熵最大化的快速独立成分分析算法对被噪声覆盖的声发射信号进行分离。试验表明：快速独立成分分析可以通过估算信号的最大非高斯性，将声发射信号和与其相互独立的环境噪声进行盲源分离，获得类声发射信号和噪声，其中获得的类声发射信号包含了真实声发射信号，便可以再通过对类声发射信号小波分解和重构的传统方法之后，将真实声发射信号的特征最大化。证实了依据独立成分分析和小波分析的独立成分分析和小波分解方法，对被噪声覆盖的声发射信号析取的有效性。本研究对木材损伤过程中被噪声覆盖的声发射信号的析取进行了初步的探索，目的是为以后木材损伤的声发射信号的降噪以及多声发射源信号盲源分离提供方法依据，同时也为其它材料的损伤声发射信号的分离提供参考。