依据不同空间约束的人工林森林经营规划模拟1)

宋博 董灵波 刘兆刚

(森林生态系统可持续经营教育部重点实验室(东北林业大学)，哈尔滨，150040)

森林经营规划可以根据森林决策者的经营意图对森林生长进行干预，是一种重要的人为干扰方式，通过不同层次的规划，可获得不同时期的经营目标。森林规划模型公式化通常包括目标函数、约束条件以及一些计算行，利用传统的数学求解方法(如线性规划、整数规划、目标规划等)或启发式算法(如模拟退火算法、门槛接受法等)获取满意解。

初期的森林经营中，规划模型通常不包含空间信息，且选取的约束条件均不涉及空间信息，如Macmillan et al.[1]使收获得净现值最大化的同时，限制了林分预定收获面积及木材收获大小，陈安峰[2]在建立异龄林收获模型时考虑采伐量、采伐强度等约束，Yousefpour et al.[3]在满足木材均衡收获的前提下建立了多目标经营规划模型，戎建涛[4]利用木材均衡收获、生长量约束、采伐强度约束等建立净收益最大化的规划模型。虽然非空间约束在森林可持续经营方面有着不可替代的作用，但一个林分采取某种经营措施必然会对其周围林分造成一定的影响，譬如大面积的皆伐不仅会造成森林景观破碎化，也会显著降低野生动植物的生境水平。随着近年来人们对森林生态的关注，越来越多的空间关系被引入森林规划模型中，任何忽略了森林空间信息的规划模型都不可能获得较好的生态环境目标[5-6]。因此，森林经营中的空间关系尤为重要，建立森林规划模型时考虑空间条件对森林效益的实现有着重要意义。

现阶段，国内外越来越多的学者在森林经营时将空间条件考虑在内，有研究者将空间结构直接加入目标函数中[7-9]，而更多学者则将其考虑在约束条件中，如Chen et al.[10]利用模拟退火算法研究如何通过调整相应的邻接矩阵产生最优的空间采伐方案。由于人们对森林生态的日益重视，研究者并不满足于单纯的相邻斑块的收获约束，而在其基础上加入回绿期和连续采伐面积的考虑，即经营措施需同时满足时间和空间的限制，如Lockwood et al.[11]基于采伐斑块的不同大小、邻接约束等条件研究森林采伐规划问题；Baskent et al.[12]建立模型时在考虑传统约束条件的同时，禁止某规划分期内同时经营相邻斑块；Bettinger et al.[13]构建了基于单元限制模型的空间规划模型以维持猫头鹰栖息地的生境水平；Richards E W et al.[14]在森林采伐和道路优化修建中考虑了最大疏开面积及绿量约束；Bettinger et al.[15]在建立野生动物生境和木材生产的综合规划模型时考虑绿量约束；Borges et al.[16]基于绿量和最大面积约束探讨了立地生产力对森林采伐作业的影响。随着国内森林作业技术的不断发展，国内也有不少学者开始将复杂的空间信息加入森林规划中，如Dong et al.[17]讨论了分别加入URM和ARM对木材净收益的影响；董灵波等[18]为了避免形成大面积连续的采伐迹地导致森林景观破碎化，用邻接约束严格禁止相邻小班在同一规划分期同时采伐，且相邻小班在回绿期内禁止采伐；孙云霞等[19]以木材均衡收获为目标函数，基于邻接约束、绿量约束和非空间约束，构建了规划期10 a的森林空间收获模型；刘雨[20]基于不同求解软件运用线性规划建立具有空间相邻约束的森林优化模型进行木材最大收获量的评估；董灵波等[21]将择伐措施的时空分布作为主要约束条件建立使经济效益最大化的森林规划模型。

随着我国经济的不断发展，木材供需矛盾不断加剧，目前国内木材需求持续刚性增长，木材对外依存度接近50%，我国已成为世界上最大的木材进口国和第二大木材消费大国[22]。为保障我国木材安全、满足经济社会发展和人民生活需要，唐守正、沈国舫等8位院士基于我国严峻的林业资源缺失现状及日益尖锐的木材供需矛盾向国务院总理联名提出建设国家储备林，借以缓解木材资源严重不足的现状。根据第九次全国森林资源清查成果显示，我国人工林面积达7 954.28万hm2，蓄积338 759.96万m3，人工林面积占森林总面积的32.94%[23]。我国是目前世界上人工林面积最大的国家，随着对天然林保护意识逐渐加强，全面禁止天然林商业性采伐，人工林成为缓解木材供应不足的重要途径，因此以木材产量为目标的人工林经营规划十分重要。

基于上述背景，本研究以黑龙江省佳木斯市孟家岗林场人工落叶松林和人工樟子松林为对象，以经营措施的3种不同空间分布形式建立森林规划模型，比较不同空间约束条件对森林经营规划结果的影响，为我国人工林的可持续经营提供理论依据。

1 研究区概况

本文研究区域位于黑龙江省佳木斯市孟家岗林场，位于桦南县，地理坐标为东经130°32′42″～130°52′36″，北纬46°20′16″～46°30′50″，林场总经营面积15 502.50 hm2，施业区属完达山系西麓余脉，地势东北高西南低，地貌为低山丘陵区，平均海拔约250 m，气候为中温带大陆性季风气候，年平均降水量约为550 mm，该林场水系为松花江一级支流倭肯河的源头汇水区。主要树种以人工落叶松(Larixgmelinii)、樟子松(Pinussylvestris)、红松(Pinuskoraiensis)为主，根据2016年森林资源二类调查数据结果，林场总蓄积1 765 756 m3。

2 材料与方法

本研究以人工落叶松林和人工樟子松林为研究对象，基于孟家岗林场2016年森林资源二类调查数据，林场共93个林班，2 282个小班，总面积15 502.50 hm2，有林地1 698个小班，占13 374.23 hm2，其中人工有林地1 396个小班，8 990.91 hm2，人工落叶松林782个小班，所有小班面积均在0.12～49.88 hm2，总面积4 675.26 hm2，人工樟子松林257个小班，所有小班面积均在0.24～49.73 hm2，总面积1 686.66 hm2。本文研究对象的初始各龄级面积及小班数统计量如表1所示。

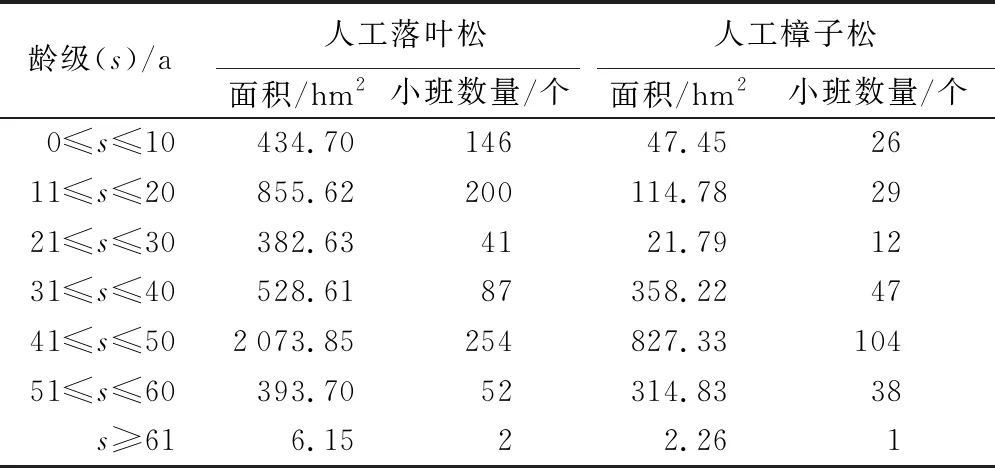
表1 研究对象各龄级期初面积及小班数统计量

本研究以孟家岗林场人工落叶松林和人工樟子松林为经营对象，建立50 a规划期(分为5个分期，各规划分期为10 a)内使木材产量最大化的森林规划模型，其目标函数的数学表达式如下：

(1)

式中：i为某小班；I为小班总数；t为某规划分期；T为规划分期总数；ai为i小班面积；Vit为i小班在规划分期t的每公顷蓄积量(由林分蓄积量预估模型预测得来)；SiPt为第t个规划分期i小班收获的决策变量。

其中，本研究各小班单位蓄积收获量预估参考王鹤智[24]所构建的黑龙江省完达山地区林分生长动态模型，经参数拟合结果分析可知其拟合效果较好，适用于本文数据，模型具体形式详见王鹤智[24]，此处不进行详述。

非空间约束。第1个约束为年龄约束，为防止过早地对中幼龄林进行人为干扰，森林经营措施应当满足最小收获年龄约束，根据《国家森林资源连续清查技术规定》(2014)中各林型的龄组划分标准设定人工落叶松林和人工樟子松林的最小收获年龄为41 a，即：

EAit≥EAmin。

(2)

式中：EAit为i小班在t规划分期时的年龄；EAmin为经营决策者所定义的不同林型对应的最小收获年龄，本文EAmin=41。

为确保各分期经济收益稳定，第2个约束为木材均衡收获约束，同传统的严格的木材均衡收获相比，本研究采用相对宽松的均衡收获约束，提高约束的可操作性，即允许各规划分期内收获的蓄积在一定范围内波动，其数学表达式为：

(1-α)VHt-1≤VHt≤(1+α)VHt-1。

(3)

式中：VHt和VHt-1分别代表第t和t-1个规划分期的收获蓄积；α为允许波动幅度，本文假定α=10%。

第3个非空间约束条件为各分期收获蓄积的最值限制，根据黑龙江省地方林业“十四五”期间年采伐限额，设定各规划分期最小采伐量为100 000 m3，各规划分期内最大收获蓄积为286 000 m3。

第4个为经营措施约束，各小班在整个规划期内至多采伐1次，其表达式为：

(4)

最后一个非空间约束为[0-1]型决策变量约束，理论上所有经营措施均可以加入到规划模型中，由于本文主要比较不同空间约束对木材收获的影响，所有本文只考虑两种相对简单的采伐措施，即皆伐和不采伐，其数学表达式为：

SiPt∈{0，1}。

(5)

空间约束。根据Murray[25]所阐述的森林规划模型中的邻接约束通常分为单元限制模型(URM)和面积限制模型(ARM)两种形式，URM主要控制经营措施的分布位置，ARM限制收获小班的面积大小。本研究采用URM约束采伐计划的空间分布，即当i小班在t规划分期被采伐时，其相邻小班k在该分期不能被安排采伐活动，其数学表达式为：

(6)

根据各小班之间的位置分布情况，可划分为3种邻接关系：①共用同一条边的两个小班；②共用一个角的两个小班；③相距有一定距离但会对彼此有影响的两个小班，本文采用ArcMap筛选出共用一条边的所有相邻小班信息作为空间约束的基础。

为了避免形成大面积连续的皆伐迹地，导致生境破碎、水土流失等生态问题，绿量约束在邻接约束的基础上考虑了森林的回绿期，即当某林分采伐后，在回绿期内(即被采伐林分再次达到郁闭前)其相邻林分严禁采伐，其数学表达式为：

(7)

式中：K为小班i的所有相邻小班的集合，m为t分期的相邻分期，Tm为绿量约束中的回绿期，当Tm=1时，m∈{t-1,t,t+1}；当Tm=2时，m∈{t-2,t-1,t,t+1,t+2}。

本文为评估不同空间约束对木材收获的影响，共建立4种规划模型，分别为传统的非空间规划模型(仅含非空间约束)以及在非空间规划模型的基础上分别加入邻接约束、绿量约束Tm=1和绿量约束Tm=2的3种空间规划模型。

3 结果与分析

上述4种基于不同约束条件的森林规划模型均为整数线性模型(ILP)，利用Lingo 11.0软件进行求解，根据目标函数和约束条件的形式，默认求解方法为分支定界法，4种森林规划模型求解过程种各项参数值如表2所示。根据各参数可以看出，有空间约束条件的规划模型形式更为复杂，且随着空间约束条件的紧缩，其公式数量越多，目标函数值越小。传统的非空间规划模型求解速度相较空间规划模型更快，空间规划模型中随着空间约束的宽松，即从Tm=2到Tm=1最后到邻接，求得全局最优解所需的迭代时间越长，迭代次数越多。经Lingo求解后可得不同情况下规划模型各分期的采伐计划，如图1所示。

图1 各规划模型50 a规划期内收获计划

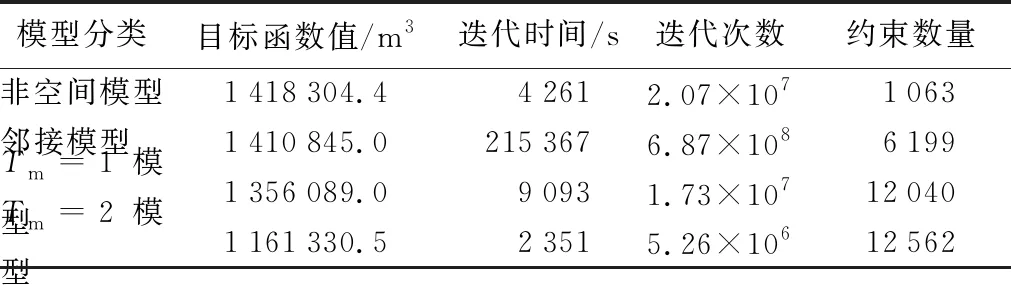
表2 Lingo求解参数值

3.1 蓄积收获量的比较

利用Lingo软件对4种模型进行求解，其规划期内蓄积收获总量结果如表2所示。传统的非空间规划模型的目标函数值最大，规划期内总收获蓄积为1 418 304.4 m3，最接近预期的目标最大限额(1.43×106m3)，加入空间约束后，规划期内总蓄积收获量减小，且空间约束条件越复杂，总蓄积收获量越小，与非空间规划模型相比，加入邻接约束、Tm=1和Tm=2的规划模型其目标函数值分别减小了约0.53%、4.39%和18.12%。根据各分期蓄积收获量变化趋势图2可知，各分期内蓄积收获量呈上升趋势，直至趋于各分期最大收获蓄积限额后稳定收获，其中Tm=2模型收获量上升趋势最为明显，非空间规划模型的各分期收获蓄积量最均衡，规划模型所受约束限制越严格，即约束条件越多，其各规划分期之间的蓄积收获量差异最大，且越难达到各分期最大限额。对4种森林规划模型的各分期蓄积收获量进行配对T检验，结果显示非空间模型、邻接模型及Tm=1模型之间无明显差异(P>0.05)，3种模型与Tm=2模型之间的P值分别为0.022、0.020、0.011，均小于0.05，故非空间模型、邻接模型及Tm=1模型的各规划分期蓄积收获量与Tm=2模型均存在明显差异。

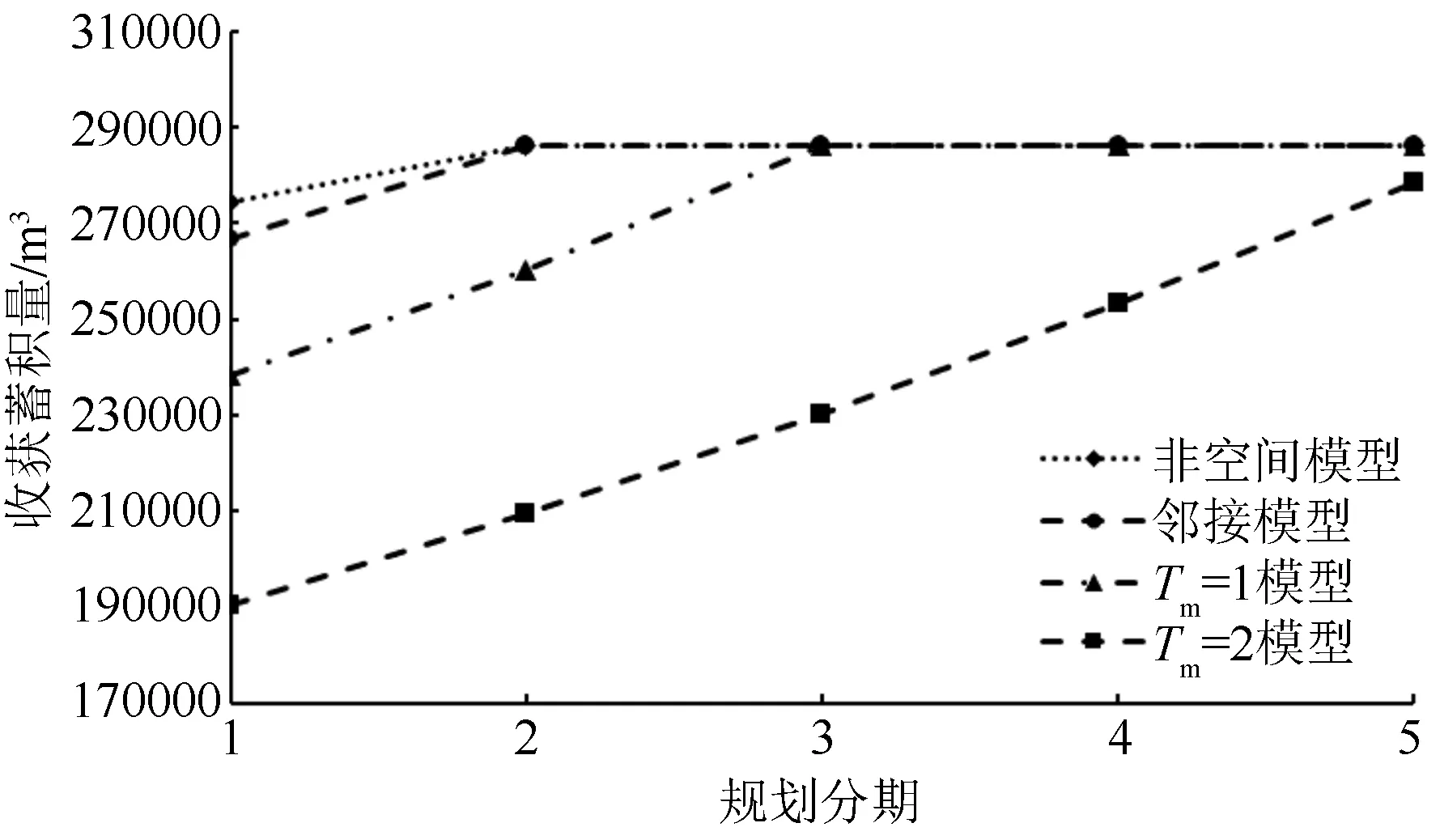
图2 各分期蓄积收获量变化趋势

3.2 收获面积的比较

经统计，4种规划模型收获面积情况如表3所示，在规划期内非空间规划模型由于对采伐措施的空间分布未作要求，故所有达到采伐年龄的小班均被采伐一次，即所有经营小班在50 a规划期内均进行了一次人工更新，且第五分期收获面积最大，邻接规划模型共收获1 027个小班，收获面积达6 338.09 hm2，约占总经营面积的99.63%；Tm=1的绿量规划模型共收获906个小班，收获面积为5 971.08 hm2，约占总经营面积的93.86%；Tm=2的绿量规划模型共收获682个小班，收获面积为4 933.45 hm2，约占总经营面积的77.55%。由此可知，回绿期越长，收获小班数越少，规划期内收获面积越小。根据各分期收获面积的计算可知，非空间规划模型中同一规划分期内最大连续采伐面积为153.20 hm2，而空间规划模型为49.88 hm2，非空间规划模型在某规划分期内最大连续采伐面积是空间规划模型的3倍，造成了大面积的采伐迹地。根据面积收获表可以看出，非空间规划模型各分期收获面积相差较大，空间规划模型的各分期采伐面积相对平稳，其中Tm=1模型各分期收获面积最均衡，能够更有效地安排人员和设备的利用。

表3 4种森林规划模型面积收获的统计特征

3.3 龄级调整结果

根据求解得到的4种规划模型各分期收获计划，可获得各模型期末的龄级面积分配情况如表4所示，森林经营的目的之一是实现法正的龄级面积分配，由表4中初始龄级面积分配可以看出该林场期初各龄级面积分配较差，第V龄级面积最大，约占总经营面积的45.6%，且成熟林面积约占总面积的56.7%，经过50 a规划期的调整，4种情况的规划模型对龄级面积结构均有所改善。由表4可得，非空间规划模型经过规划期的经营，期末无VI、VII龄级，其中幼龄林面积最多，占总面积的40.9%，不考虑采伐措施的空间分布会对森林造成过度采伐，不利于森林的永续利用。经过5个10年规划分期的经营后，考虑空间约束的3种模型，I-V龄级的面积均趋于法正的龄级分配，其中Tm=1模型的调整效果最好，I-V龄级面积依次为1 262.83、1 241.19、1 186.29、1 136.80、1 143.97 hm2，各龄级面积比值为21∶21∶20∶19∶19。

表4 规划初期及末期各龄级面积分配量

4 讨论

本文以50 a规划期内最大化木材产量为经营目标，比较非空间约束及不同绿量期对蓄积收获的影响。经敏感性分析可得，相较传统的非空间模型而言，加入空间约束对木材蓄积收获会有不同程度的影响。空间约束中的邻接约束未考虑绿量期，相当于Tm=0的绿量约束，由于该约束条件下相邻小班采伐间隔期仅为一个规划分期，回绿期较短，约束相对宽松，该约束条件下的规划模型与非空间收获模型结果差异较小，木材总收获量仅减小了0.53%，可忽略不计。Tm=1的绿量约束下木材蓄积收获总量较非空间模型减少4.39%，方差分析结果显示，二者差异不明显。由此可知，邻接约束和Tm=1绿量约束对木材蓄积收获量不敏感。当回绿期Tm=2时，总木材产量比非空间模型的结果减少18.12%，其二者的各分期蓄积收获量经方差分析得P=0.011<0.05，Tm=2绿量约束模型与非空间模型差异极显著。综上，随空间约束限制性的加强，对木材收获的影响越明显，即考虑的回绿期越长木材产量越小。

Boston et al.[26]比较了最大皆伐面积不同时，回绿期从3 a减至2 a对木材收益净现值的影响，研究表明，增加最大采伐面积时，缩短绿量期对净现值的影响程度有所降低。董灵波等[27]评估了规划分期为1 a时非空间约束以及Tm=2绿量约束对木材收益的影响，其研究结果表明，加入绿量期为2个规划分期的URM模型结果与非空间规划结果差异显著。本研究假定各规划分期为10 a，得到的结果与董灵波等相似，说明考虑2个规划分期作为绿量约束会对结果产生较大影响，除此之外，本文还比较了不同长短的绿量期对规划结果的影响，目前针对该方面的相关研究还较少。

虽然非空间规划模型得到的木材产量最大，但该约束情况下未考虑采伐措施的时空分布情况，最大连续皆伐面积是加入空间约束的3倍，大面积的皆伐迹地会导致水土流失、生境破碎化等严重的生态问题，不利于森林经营后续的补植更新等造林措施。3种不同的空间约束条件中，Tm=2绿量约束下虽然经营措施的空间分布效果最好，但规划期结束时，第VII龄级面积占总面积的18.09%，即规划期末过熟林面积过多，未充分利用木材资源。从各分期蓄积收获情况来看，邻接约束与Tm=1绿量约束之间无明显差异(P=0.179)，Tm=1时各分期采伐的小班面积比邻接约束更均衡，更利于合理安排人员工作及设备的分配，且从规划期末对龄级面积分配调整结果来看，Tm=1约束下的第I-V级面积分配更趋于法正林结构。综合蓄积、面积、龄级以及经营措施空间分布等多方面因素考虑，基于Tm=1绿量约束下的森林规划模型效果最佳。需要特别指出说明的是，由于数据的局限性，本研究结论仅适用于孟家岗林场人工落叶松林和人工樟子松林的经营，该地区其他林型如人工红松林等，由于其主要经营价值不在于木材产量，故本文未将其考虑在内，后续的研究中可以通过收集每年红松林球果产量等数据，将红松林的经营加入规划模型中建立更完善的森林规划方案。

5 结论

本研究以孟家岗林场人工落叶松林和人工樟子松林的经营为例，利用Lingo11.0软件对目标函数进行求解，评估并比较不同绿量期的空间约束对森林收获调整的影响。结果表明，在传统经营模式的基础上考虑森林收获作业的时空分布对木材产量有不同程度的影响，其中考虑2个规划分期作为绿量期时产生的影响最为明显，随着绿量期的延长，规划期末木材产量逐渐下降。在规划期初始龄级面积分配不均的情况下，仅考虑传统的约束条件虽然能获得最大木材产量，但无法兼顾经营地区水土保持、生境保护等生态效益，而适当地加入空间约束可以在保证木材产量的同时，更有利于森林的可持续经营，本文中绿量期为1个规划分期时期末龄级面积结构调整效果较好。此处需要特别强调的是，本文采用的是孟家岗地区2016年森林资源二类调查数据，数据采集时间较近，对未来短期内的森林作业有一定的理论指导意义，但由于野外不可控因素过多，在实际操作中应尽可能根据现实情况及时做出相应调整。