基于绝对节点坐标法的三维柔性旋转梁动力特性分析

张海波，夏鸿建，李德源，刘佳宇

（广东工业大学 机电工程学院, 广东 广州 510006）

随着柔性梁在航空、航天和风力机等领域的广泛应用，研究者越来越重视其高精度的动力特性分析。如直升机螺旋桨[1]、风力发电机叶片[2]等,这类梁结构具有明显的非线性变形特点，工作时存在不同的回转速度。精确控制柔性旋转梁，需准确分析柔性梁的时域和频域特性。工程中为提高分析效率，通常采用简化梁模型，主要有线性有限元法、模态坐标近似法和柔性多体系统法，但这些方法存在模型精度较低、动力刚化模拟不明显、转动模态仿真不准确等问题。直接采用有限元模型，虽然能精确描述梁结构，但由于自由度显著增加，难以将其用于后续的多场耦合分析。现在计算大转动、非线性大变形梁的动力学问题的主流方法有GEBF(Geometrically Exact Beam Formula)和ANCF(Absolute Node Coordinate Formula)[3]。前者在机翼气弹耦合分析领域得到广泛应用，但存在梁截面姿态插值问题，且广义坐标包含角度和位移，给频域分析的线性化处理带来较大困难。绝对节点坐标法由于质量矩阵为常数矩阵，且直接基于连续介质理论，能方便描述梁的几何非线性特征，并支持高效的时域求解。此外，在构建频域线性化动力学方程时，仅需对刚度矩阵线性化，因此适用于柔性旋转梁模型的时域和频域分析建模。目前，国内外已有专家开展了广泛研究。

Ahmed[4]介绍了绝对节点坐标公式的计算机实现过程，为后续的数值仿真奠定了基础。Zhang等[5-6]使用不同插值函数的ANCF对平面梁进行了动力特性分析，研究了弯曲和拉伸振动之间的模态耦合现象，但缺少弯扭耦合的相关研究。郑彤等[7]对三维大变形柔性梁系统的动力学建模和仿真进行了研究。建立三维大变形柔性梁系统的动力学模型，解决了ADAMS在计算大变形物体动力学时的局限性问题，但并未涉及动力特性分析。赵春璋等[8-12]建立动力学模型,研究了平面柔性梁大范围转动的变形、仿真精度的影响以及不同梁的理论适用范围，但未对频域响应进行相关的研究。姚震等[13-14]对ANCF的精确性和灵敏度展开了研究，认为不同材料和截面特征对系统末端的运动规律有一定影响，同样未涉及动力特性分析方面的工作。

综上，目前研究主要集中于平面梁的动力学仿真和弯曲梁小变形情况下固有频率的计算，对基于连续介质理论和非线性变形假设的三维柔性旋转梁动力刚化及其动力特性的研究相对较少。

为此，本文基于绝对节点坐标法，结合连续介质理论和几何非线性假设，建立三维柔性梁的动力学模型。通过非线性梁自由单摆仿真实验，验证本文算法的精确性；然后对三维梁的动力学方程进行线性化，构建柔性旋转梁的频域振动方程，计算不同转速下梁的动力刚化现象，并研究柔性旋转梁在不同转速下的模态振型变化。为后续风力机或飞机叶片等的气弹阻尼分析提供指导。

1 绝对节点坐标柔性梁建模

1.1 梁单元位置插值

图1为三维二节点梁单元。其中，OXYZ为绝对坐标系，(x,y,z)为梁单元中任意一节点在单元坐标系中的坐标。rp为梁单元中线上任意一点p在绝对坐标系中的位置矢量；r1，r2，r3，X，Y，Z为该点三维坐标参数；e(t)为 绝对坐标系中的单元节点坐标；S(x,y,z)为单元形函数。

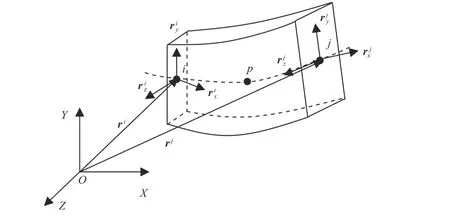
图1 三维变形梁单元Fig.1 Three dimensional deformed beam element

本文采用三次插值多项式来描述单元中任意一点的绝对位置。

式中：ai、bi、ci为 待定系数，x、y、z为梁单元未变形时该点在单元坐标系下的坐标。

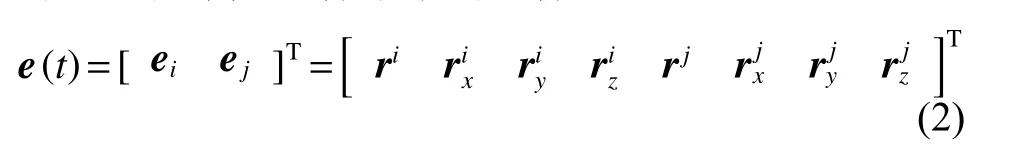
式中：ri、rj分 别表示单元首尾节点在OXYZ下的位置矢量；rx表示位置矢量对梁单元坐标x的偏导数矢量，ry、rz同理。

将单元坐标式(2)与三次插值多项式联立，求解待定系数，可得到单元形函数[15]。

式中：I为3 ×3的单位矩阵。

式中： ξ=x/l，η =y/l，ζ =z/l，l为未变形时梁的单元长度。

1.2 单元质量矩阵

梁单元的动能可表示为

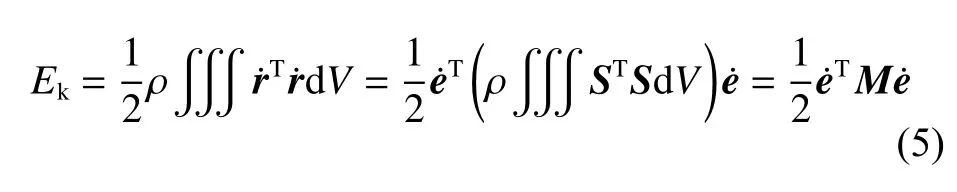
式中：M为单元质量矩阵，该矩阵与广义坐标无关，为常数矩阵。

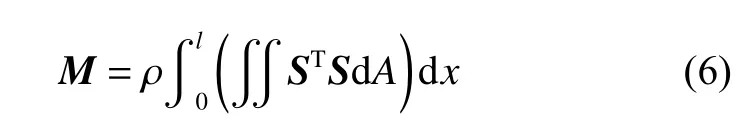
式中： ρ、 dA、l分别为梁单元的密度、截面面积微元、梁未变形时的单元长度。

1.3 单元刚度矩阵

利用连续介质理论和非线性格林应变张量假设，计算梁单元的位移应变关系。梁单元的变形梯度H为

非线性格林应变张量为

将式(1)和式(7)代入式(8)得到

式中：

将对称的非线性格林应变张量表示为列矢量形式。

在线弹性本构关系下，应力σ 与 应变ε 的关系为

式中：D为材料弹性系数张量。

根据虚功原理弹性力所作虚功为

式中：K为单元刚度矩阵，V为梁单元的体积，可将单元刚度矩阵整理得到式(13)。

式中：Kl为刚度矩阵的线性部分，与绝对节点坐标无关。

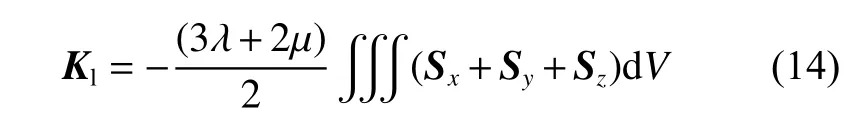
Kn为非线性部分，Kn=Kn,1+Kn,2+Kn,3，其中λ 、µ为lame常数，具体计算为

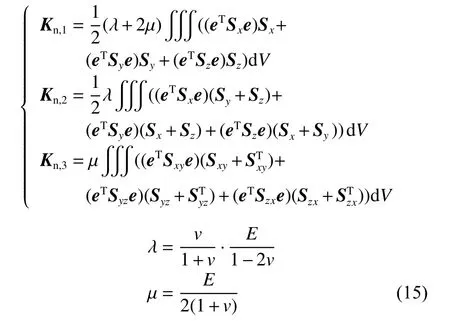
式(15)中：E为材料的弹性模量，v为材料泊松比。

1.4 单元广义力矩阵

根据虚功原理以及式(1)，得到外力虚功为

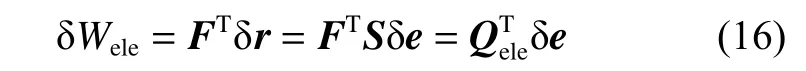
式中：r是节点的位置矢量,F为梁单元上任意一点所受的外力，是与单元节点坐标相关的广义力的矢量。

2 柔性梁系统动力学方程

2.1 系统的约束表达

单摆仿真时，需要在单摆被约束的根部施加一转动副约束，使单摆绕着被约束点旋转，此外该转动副亦可施加于梁与梁之间，形成两梁之间的相对转动；多个梁单元时，单元与单元之间不会发生相对移动、扭转和旋转，单元与单元需固结在一起。故本文特介绍2种约束，一种为绕z轴旋转的自由单摆的转动副约束，一种为梁单元之间的固定铰约束。

转动副约束定义如图2(a)所示，点p是两单元连接处的节点，故两单元在点p处的绝对位置坐标和z方向的偏导坐标始终相同，x和y方向的偏导坐标可以不同。其约束方程为

固定铰约束如图2(b)所示，点p在i单 元和j单元中的绝对位置坐标和偏导坐标始终相等。其约束方程为

式中：rip为i单 元中p点 的绝对坐标矢量，r为i单元中p点关于单元坐标的偏导数。

2.2 系统动力学方程

由单元质量矩阵、单元刚度矩阵、单元广义力矩阵和组装布尔矩阵B，可获得梁模型的质量矩阵Mtm、刚度矩阵Ktm、广义力矩阵Qtm。

B是m×n维 的组装布尔矩阵，m为梁单元坐标数与单元数目的乘积，n为柔性梁系统节点坐标数[16]。

考虑梁铰约束，将约束式(18)～(20)与式(21)联立。约束组装矩阵由Bc表 示，e¨为加速度，约束柔性梁的动力学方程可表示为

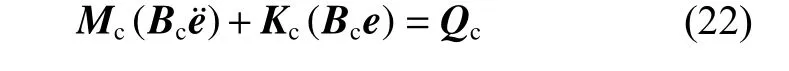
式中：Mc为约束后的质量矩阵，Kc为约束后的刚度矩阵，Qc为约束后的广义力矩阵。

2.3 旋转梁动力学方程

用绝对节点坐标方法建模时，节点坐标相对绝对坐标进行定义。当梁绕定轴转动时，为方便描述刚性大范围定轴转动和梁本身的变形运动，引入浮点坐标系，建立旋转梁动力学模型。

在三维空间坐标中，三维柔性梁绕着Z轴旋转，将其投影于旋转平面如图3所示。

图3中r1、r2、η1、η2分别表示点在绝对坐标系下的坐标和浮动坐标系下的坐标， θ为浮动坐标系相对于绝对坐标系的转角。该点在两坐标系中的关系如式(23)所示。

根据单元节点坐标e(t)的表示，结合式(23)，单元浮动坐标e˜ele与单元节点坐标e(t)关系为

式中：eele,R为轮毂半径坐标，R为轮毂半径。

式(25)～(26)中：V为单元坐标组装的布尔向量，NCT为单元节点坐标变化矩阵。

将式(24)代入式(22)中，旋转梁动力学方程为

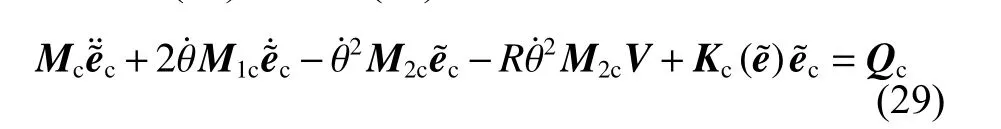
式中：M1c、M2c为做了不同变化后的质量矩阵， θ˙为旋转角速度，e˜ 为浮动坐标向量，e˜c=Bce˜为系统约束后的浮动坐标向量，e¨˜c为 加速度，e˙ ˜c为速度。

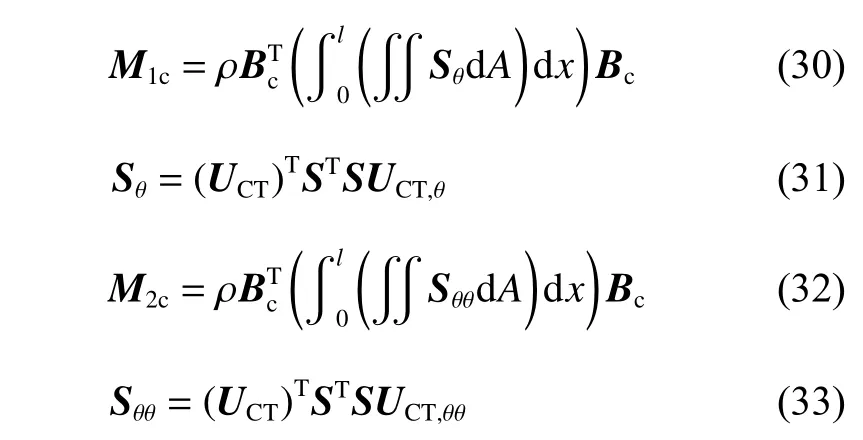
UCT为2 4×24 的 单 元 坐标 变 化 矩 阵，UCT,θ和UCT,θθ分别为其对旋转角度的一阶导数和二阶导数。联合式(24)～(33)，计算得M1c和M2c为常数矩阵[17]。

2.4 旋转梁动力学方程线性化

为了分析柔性旋转梁的频率特性及其模态变化，采用摄动理论对旋转动力学方程式(29)分别进行、和的线性化。获得旋转梁振动方程为

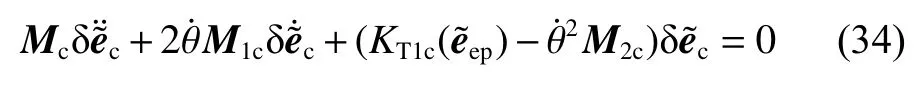
式中：KT为 切线刚度矩阵,KT1为切线刚度矩阵的线性部分，˜ep为 当前旋转振动梁的平衡位置，KT1c(ep)表示约束后的KT1(ep)，约束方式与前一节相同。

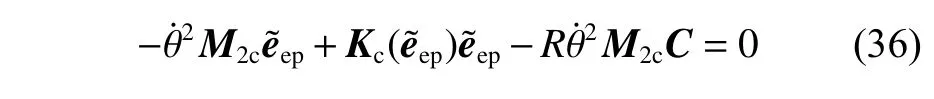
式中：j为 虚数，t为摆动时间，ω 为固有频率，Z为复杂列向量常量，KT为切线刚度矩阵。

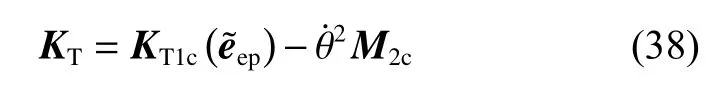
3 仿真案例

3.1 自由单摆动力学仿真

以自由单摆仅受重力作用下的动力学仿真为例，验证本文方法所建梁模型的精确性。此时外力F为重力，是梁所受的体积力。

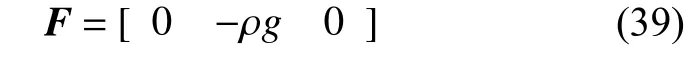
根据形函数S和式(17)、式(39)可得到单元广义分布重力的表达式

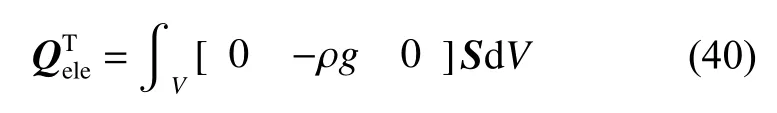
式(39)～(40)中： ρ为柔性梁密度，g为重力加速度。

自由单摆如图4所示，柔性梁截面高为h，截面宽为w， 总长为L，质量为m。

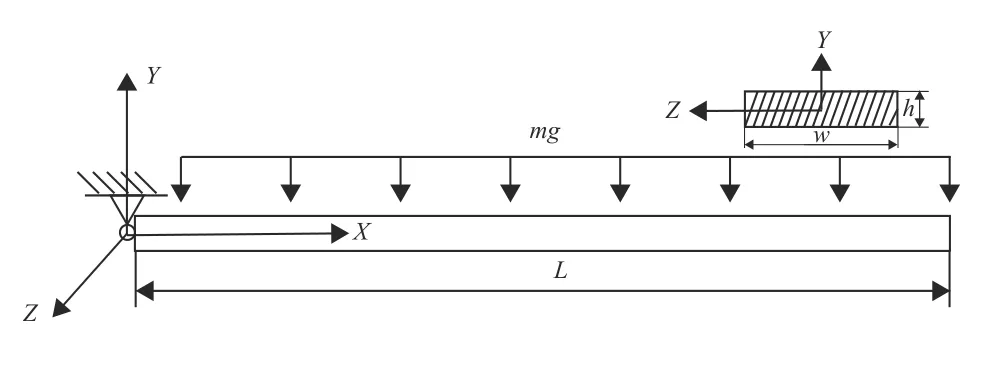
图4 自由柔性单摆Fig.4 Free flexible pendulum

本文根据文献[12]中的算例进行了仿真实验1：弹性模量E为0.8 MPa，泊松比ν 为0.3，截面高h为0.02 m，截面宽w为0.08 m，总长L为1.2 m，密度ρ 为5 540 kg /m3，将单摆分成12单元。图5为仿真实验1中柔性单摆不同时间下的位置及形状，表1为仿真实验1与文献[12]的算例在t=0.3 s时的实验结果对比，证明了本文所采用的模型具有较高的准确性。

图5 仿真实验1柔性单摆不同时间下的位置及形状Fig.5 Position and shape of flexible pendulum at different time

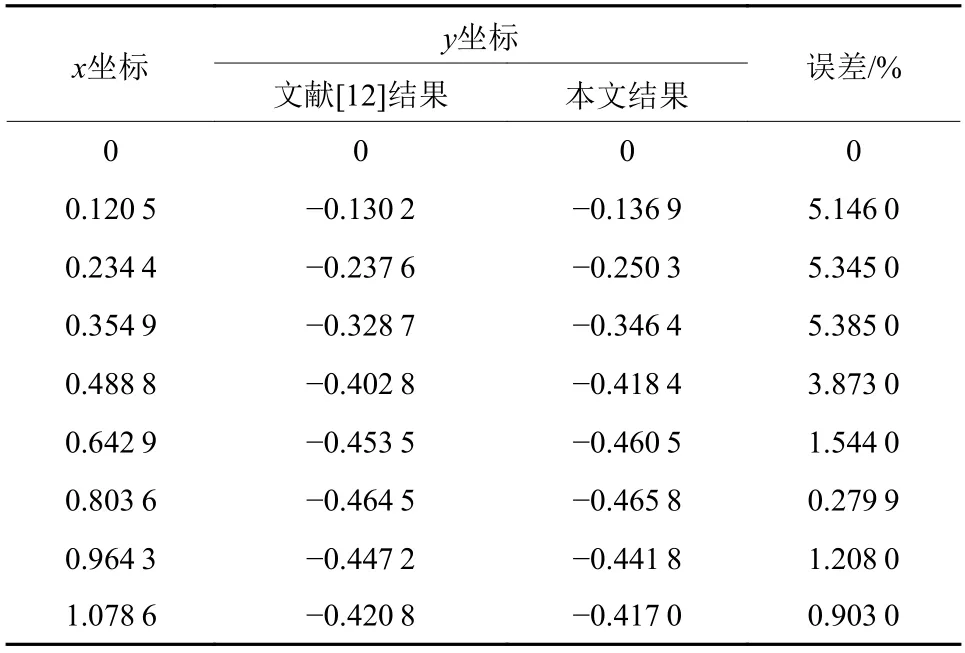
表1 本文的仿真结果与文献[12]实验结果的对比(t=0.3s)Table1 Comparison between simulation results and literature[12] in this paper (t=0.3 s)

本文也对文献[18]中的算例进行了仿真实验2，其弹性模量E为2 MPa，泊松比ν 为0.3，截面高h为0.01 m，截面宽w为0.01 m，总长L为1.0 m，密度ρ 为7 200 k g/m3。图6(a)为仿真实验2中柔性单摆不同时间下的位置及形状，表2为仿真实验2和文献[18]的算例在t=0.4 s时的实验结果对比，两者结果基本一致，进一步验证了本文方法的准确性。图6(b)为单摆能量曲线图，其中纵坐标为能量Ewhole，横坐标为时间t，Ek为动能，Ep, ela为弹性变形能，Ep, g为重力势能，Etotal为总能量。从图中可以看出整个仿真过程中机械能始终守恒。

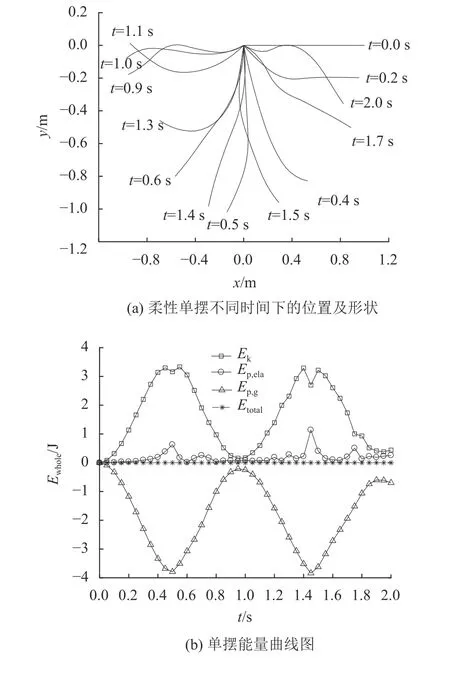
图6 仿真实验2柔性单摆不同时间下的仿真结果Fig.6 Simulation results of flexible pendulum at different time

表2 本文仿真结果与文献[18]实验结果的对比（t=0.4 s）Table2 Comparison between simulation results and literature[18] in this paper (t=0.4 s)

3.2 非线性柔性梁固有频率的计算

3.2.1 柔性旋转梁固有频率的计算

为了验证旋转梁动力特性仿真精度，本文计算不同转速下的无量纲固有频率，并与文献[19]的计算结果进行对比。ωi是指不同阶数的固有频率，无量纲固有频率用不同阶数的固有频率与0阶的固有频率的比值表示，即ωi/ω0。

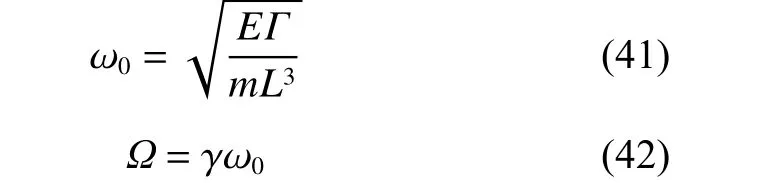
式(41)～(42)中：E为柔性梁的弹性模量，Γ 为截面惯性矩，m为柔性梁的质量，L为柔性梁的总长度，Ω 为无量纲旋转速度，γ 为转速。

不同转速下无量纲固有频率前三阶计算结果如表3所示，两者结果基本一致，验证了旋转梁动力特性仿真精度。

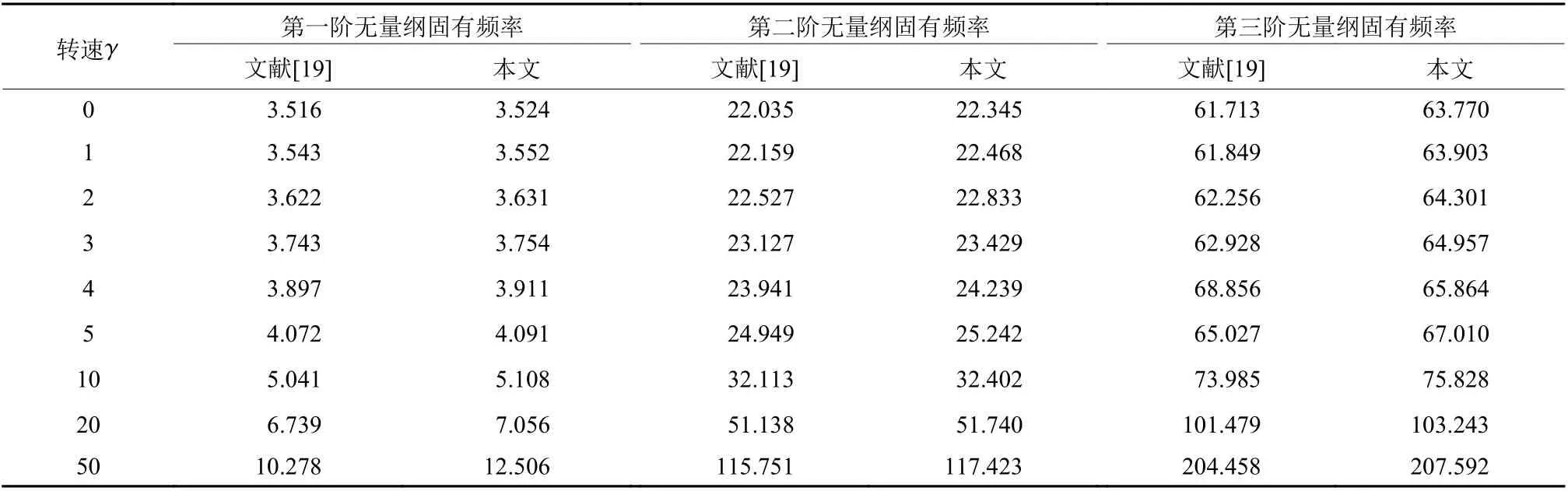
表3 不同转速下无量纲频率前三阶的结果对比Table3 Comparison of the results of the first three orders of dimensionless frequencies at different speeds

3.2.2 不同转速下的各阶振型

梁模型的空间位置如图4所示，设置弹性模量E为5 ×108Pa，泊松比ν 为 0.3，截面高h为0.02 m，截面宽w为0.2 m，总长L为8.0 m，密度ρ 为2 677.67 k g/m3，将单摆分成10单元进行仿真。绘制了不同转速下的前6阶模态振型，并将各阶振型投影到旋转平面(xy平面)或垂直于旋转平面的平面(xz平面)。

如图7～9所示，z方向模态振型从静止时的第3阶振型，变为了图8中转速为10 r/min的第2、6阶振型以及图9中转速为100 r/min的第2、4、6阶振型。随着转速的增加，前6阶中垂直于旋转平面(z方向)的振型所对应的频率会逐渐转换为低阶频率。图10中，转速为140 r/min，y方向出现了3阶的振型，z方向出现了2阶振型，第6阶为扭转振型；图11中，转速为300 r/min，y方向出现了2阶的振型，z方向出现了2阶，第4阶为扭转振型，第6阶为拉伸振型。从此可见，随着转速的增加，扭转和拉伸模态振型所对应的频率会逐渐转换为低阶频率。

图7 静止时前六阶振型Fig.7 The first six modes at rest

图8 10 r/min前六阶振型Fig.8 The first six modes at 10 r/min

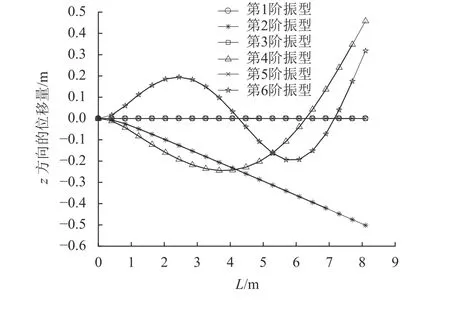
图9 100 r/min时前六阶振型Fig.9 The first six modes at 100 r/min

图10 140 r/min时前六阶振型Fig.10 The first six modes at 140 r/min

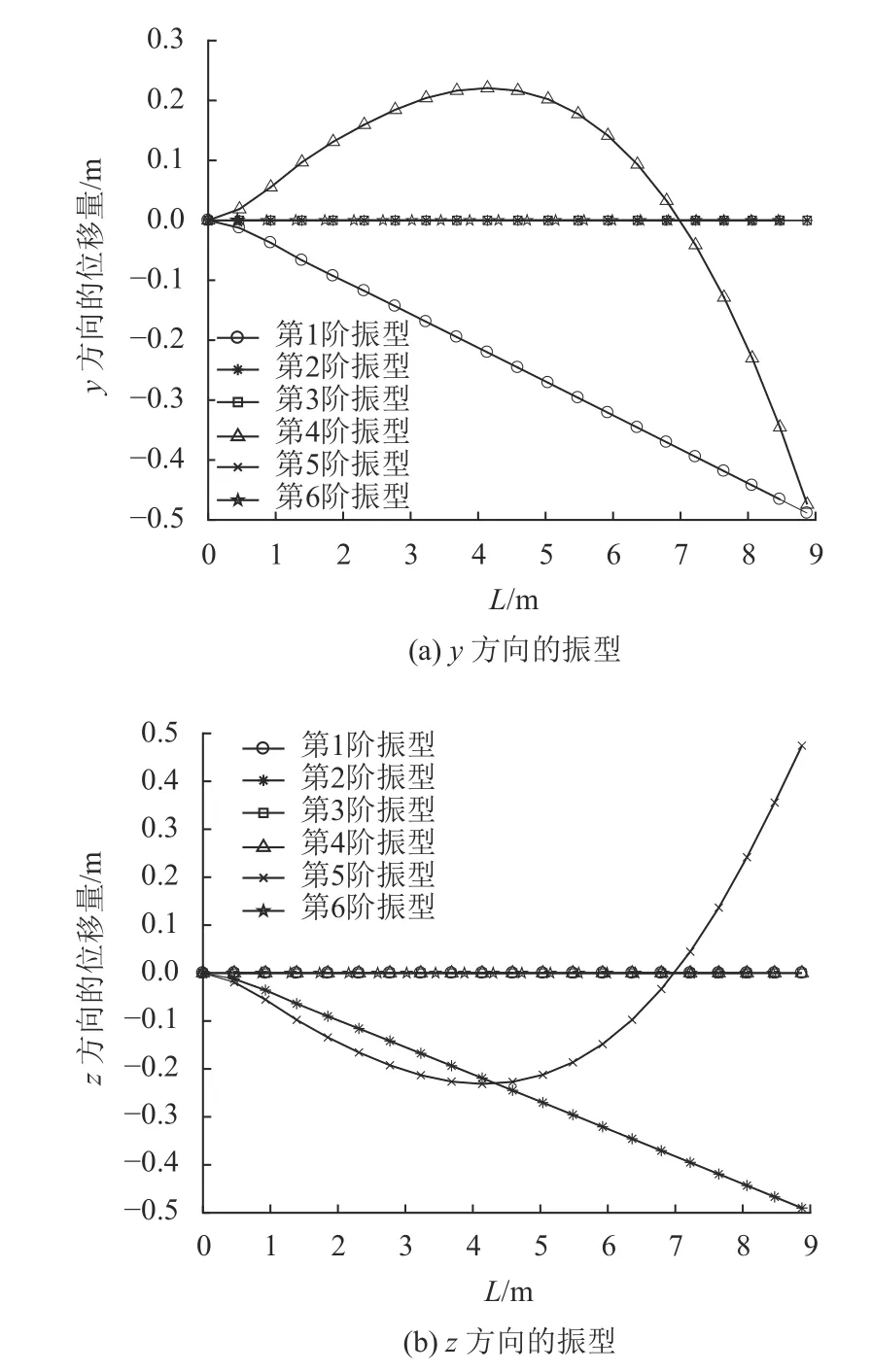
图11 300 r/min时前六阶振型Fig.11 The first six modes at 300 r/min

4 结论

本文在绝对节点坐标法基础上，运用连续介质理论推导了三维柔性梁的动力学方程，并对不同文献中的单摆案例进行了仿真，验证了本文方法的有效性。然后对动力学方程进行了线性化处理，计算了不同转速下柔性旋转梁的无量纲固有频率，并分析了非线性柔性旋转梁在不同转速下的模态振型变化特性。通过三维柔性梁动力学建模与动力特性的研究可得到以下结论。(1) 本文所建非线性梁模型能精确分析三维柔性梁的时域动力学响应；(2) 带浮动坐标的绝对节点坐标建模方法，能有效分析柔性旋转柔性梁的频域振动特性；(3) 三维柔性旋转梁随着转速的增加出现动力刚化现象，且垂直旋转平面的模态振型以及扭转和拉伸模态振型所对应的频率会转化为低阶频率。