不同参数对翼型外流场力系数数值仿真的影响
李 芃
(铜陵学院 电气工程学院, 安徽 铜陵 244000)
外流是浸没在流体中物体外围的流动,流体流经翼型表面会在垂直于表面的方向产生压力,在平行于表面的方向产生剪切力。压力与剪切力合力在流动方向的分量称为阻力,在垂直于流动方向上的分量称为升力,它们的研究对翼型设计具有指导意义。传统方法可通过风洞实验测量出阻力和升力[1-2],但风洞实验准备周期较长,且耗资不菲。随着计算机硬件的发展和数值模拟技术的进步,可采用计算流体力学软件CFD求解流体运动控制方程获得阻力和升力。该方法周期短、效率高、花费少,目前已成为研究翼型外流场的主要方法[3-4]。无量纲阻力系数Cd和升力系数Cl是用于表征物体阻力和升力特性的关键系数,本文以NACA0012翼型为研究对象,通过CFD软件Ansys-fluent分析了翼型后缘形状、湍流模型和远场距离在不同攻角下对Cd和Cl数值仿真的影响,以期对翼型外流场的数值仿真研究有所借鉴。
1 仿真基础
根据文献[5-7]提供的自由来流条件和试验数据分析不同参数对翼型外流场关键系数数值仿真的影响,分别采用Airfoil tools(UIUC Airfoil coordinates database)和NACA 4 digit airfoil generator设计了2种NACA0012二维翼型,翼型弦长L=1 m。根据Airfoil tools提供的132个数据点设计的翼型后缘是钝型,采用3D curve导入Ansys DesignModeler时可看到后缘处没有闭合,如果不手动将后缘两点连接,而是直接生成二维平面,后缘处会形成类似椭圆形的钝型,导致在mesh中划分网格失败。采用NACA 4 digit airfoil generator,选中close trailing edge设计包含200个数据点尖后缘翼型。2种模型如图1所示,可以看到数据点位置存在明显不同。试验雷诺数Re=6 × 106,对外部流动,沿表面位置分布的雷诺数大于5 × 105可认为流动状态为湍流,因此要考虑湍流对翼型外流场的影响。
1.1 湍流模型
湍流是一种流体流动状态,此时的流体做不规则运动。描述流体运动的NS方程是封闭方程组,但是直接数值模拟(DNS)需要非常大的计算资源,难以在实际中得到应用。目前普遍采用雷诺平均(RANS)方法对湍流脉动进行时间项的平均化处理,通过简化时间项降低对计算资源的要求。但同时增加了新的缺少控制方程的未知量导致NS方程不封闭,需要选择合适的湍流模型来封闭描述湍流的方程组。选择合适的模型描述湍流是数值仿真的关键,对大多数数值仿真应用,Spalart-Allmaras、SST K-ω和K-ε是被广泛接受的较为精确的RANS湍流模型。

(a)两种不同的翼型模型示意图 (b)数据点位置的近景图
1.2 网格划分
黏性是流体内部黏滞性的度量,所有流体流动均涉及某种程度的黏性效应。黏性导致直接与翼型壁面接触的流体被粘在表面无滑移,即无滑移条件。由于无滑移条件的作用,在临近翼型壁面非常小的法向距离内,流体速度会从较大的数值减少到与壁面的相同速度,导致壁面的法向速度具有非常大的梯度,形成速度剖面,黏性效应产生的速度梯度显著的区域称为边界层。边界层是物体表面附近薄的粘性层,包含了所有的粘性效应,而边界层外面的流动是无粘的。相关系数的计算与粘性边界层息息相关,为了使数值仿真的结果更加贴近真实情况,翼型临近壁面的网格划分十分关键,尤其是第一层网格高度yH。对翼型临近壁面边界层参数的求解一般有2种方法:(1)求解粘性子层,(2)利用壁面函数。Spalart-Allmaras(SA)、SST K-ω湍流模型采用NS方程求解黏性子层的流动物理量分布,不采用壁面函数,需要满足y+≤1。K-ε湍流模型采用壁面函数,需要满足30 ≤y+≤300。本文采用求解粘性子层的办法,基于Spalart-Allmaras和SST K-ω湍流模型进行翼型外流场的网格划分[8-9],需要满足y+≤1以确定第一层网格的高度。雷诺数Re计算公式如公式(1)所示,其中L是特征长度,μ是动力黏度,U是自由来流速度,ρ是空气密度。
(1)
Cf是壁面摩擦系数,计算公式如下:
Cf=[2lg(Re)-0.65]-2.3
(2)
壁面切应力τW的计算公式如下:
(3)
根据壁面切应力可计算摩擦速度uτ:
(4)
y+的计算公式如下,其中yP是第一层网格中间位置到壁面的距离:
(5)
根据公式(1)~公式(5)可计算出yP,第一层网格高度yH=2yP。本文的试验参数如下:Re=6 × 106,L=1 m,μ=1.81 × 10-5kg·m-1·s-1,ρ=1.225 kg·m-3,U=88.65 m·s-1,代入上述公式可计算得到yH=4.4 × 10-6m。
常用的网格划分工具有mesh、ICEM CFD、pointwise等,本文采用Ansys内置的ICEM CFD。官方建议翼型外流场数值仿真的远场距离一般应12~20倍于翼型的弦长L,分别选取了12 m、16 m和20 m绘制C型外流场并进行网格划分,外流场输入边界和输出边界命名为inlet和outlet,翼型表面命名为airfoil。采用ICEM CFD对设计的2种翼型进行网格划分,考虑到后缘具备钝型和尖型2种形式,采用了类似的网格分块形式:对钝型后缘翼型,应用类似“鱼尾”的形式划分网格,保留后缘处的块。对尖后缘翼型,折叠后缘处的块。由于边界层第一层的网格高度对Cd等参数的计算有直接影响,所以在临近翼型壁面处再进行一次分块。钝后缘和尖后缘处的网格划分如图2所示。

(a)钝后缘 (b)尖后缘
网格划分的难点在于如何在较大的外流场范围内保证较好的网格质量,且网格数量不能太大。评价参数aspect ratio和determinant是2个重要指标,为了满足y+≤1的条件,yH计算数值为4.4 × 10-6m,极易使aspect ratio的最大数值超过10 000,进而在fluent仿真环境下出现浮点溢出或计算发散等错误导致仿真失败。对本文二维翼型和远场条件而言,测试表明应尽量使划分网格aspect ratio的最大值在5 000以内,determinant最小值大于0.8。为了保证数值仿真结果的可靠性进行了网格无关性测试,生成的网格数量为580 000。对钝后缘,12 m、16 m和20 m的远场距离下aspect ratio的最大值和determinant的最小值分别为(2 200,0.894)、(2 920,0.89)和(3 800,0.863)。对尖后缘,12 m、16 m和20 m的远场距离下aspect ratio的最大值和determinant的最小值分别为(1 680,0.839)、(2 280,0.886)和(3 640,0.875)。
2 数值仿真
计算机仿真环境参数如下:CPU AMD Ryzen 7 5800X 8-core processor,RAM DDR4 64G,操作系统WIN10 64专业版,Ansys 2020 R2版本,Fluent仿真环境采用双精度、8核并行处理方式。启动Ansys-fluent,采用press-based压力基求解器进行稳态计算,输入边界inlet类型为velocity-inlet,velocity specification method选择magnitude and direction,攻角为0°时来流方向x分量为cos(0°)=1、y分量为sin(0°)=0,攻角为10°时来流方向x分量为cos(10°)=0.984 8、y分量为sin(10°)=0.173 6,攻角为15°时来流方向x分量为cos(15°)=0.965 9、y分量为sin(15°)=0.258 8。输出边界outlet类型为pressure-outlet,除turbulence外其他保持默认参数。翼型表面airfoil类型为wall,选择no slip无滑移条件。参考值的设置影响Cl和Cd的计算,因为是2D模型,depth默认为1,area=depth*length,length是特征值长度。对二维翼型,length =L=1,所以area=1。流速和动力黏度取试验数值,其他参数取默认值。采用coupled耦合算法,flow选择二阶迎风型。设置Cl和Cd的reports以便分析,force vector的取值与攻角直接相关:当攻角为0°,Cl的x=-sin(0°)=0、y=cos(0°)=1,Cd的x=cos(0°)=1、y=sin(0°)=0;当攻角为10°,Cl的x=-sin(10°)=-0.173 6、y=cos(10°)=0.984 8,Cd的x=cos(10°)=0.984 8、y=sin(10°)=0.173 6;当攻角为15°,Cl的x=-sin(15°)=-0.258 8、y=cos(15°)=0.965 9,Cd的x=cos(15°)=0.965 9、y=sin(15°)=0.258 8。初始化选用基于拉普拉斯方程的hybrid非均匀方法,迭代5 000次。因NACA0012是对称翼型,攻角为0°时升力非常小,升力系数近似为0。在进行数值仿真时计算得到的升力系数量级为10-6,可近似为0。
2.1 Spalart-Allmaras模型数值仿真
湍流模型选择Spalart-Allmaras,输入边界inlet的turbulence specification method选择turbulent viscosity ratio,turbulent viscosity ratio取值1,空间离散算法的相关参数都选择二阶迎风型。翼型外流场远场距离为12 m,攻角分别为0°、10°和15°时的数值仿真结果如下:(1)对钝后缘,攻角为0°,Cd=0.008 155 016 4,Cl=0;攻角为10°,Cd=0.014 346 259,Cl=1.072 940 1;攻角为15°,Cd=0.024 874 452,Cl=1.523 896 3。(2)对尖后缘,攻角为0°,Cd=0.008 094 270 9,Cl=0;攻角为10°,Cd=0.014 131 926,Cl=1.067 112 5;攻角为15°,Cd=0.024 498 527,Cl=1.518 368。
翼型外流场远场距离为16 m时,攻角分别为0°、10°和15°时的数值仿真结果如下:(1)对钝后缘,攻角为0°,Cd=0.008 195 890 1,Cl=0;攻角为10°,Cd=0.013 932 938,Cl=1.077 611 6;攻角为15°,Cd=0.024 260 434,Cl=1.525 901。(2)对尖后缘,攻角为0°,Cd=0.008 117 424 6,Cl=0;攻角为10°,Cd=0.013 799 076,Cl=1.071 497;攻角为15°,Cd=0.024 209 021,Cl=1.516 862。
翼型外流场远场距离为20 m时,攻角分别为0°、10°和15°时的数值仿真结果如下:(1)对钝后缘,攻角为0°,Cd=0.008 158 128 6,Cl=0;攻角为10°,Cd=0.013 608 489,Cl=1.078 626 4;攻角为15°,Cd=0.023 542 659,Cl=1.529 061 9。(2)对尖后缘,攻角为0°,Cd=0.008 094 481 7,Cl=0;攻角为10°,Cd=0.013 821,Cl=1.067 038;攻角为15°,Cd=0.025 963 382,Cl=1.493 103 7。
2.2 SST K-ω模型数值仿真
湍流模型选择SST K-ω,输入边界inlet的turbulence specification method选择intensity and viscosity ratio,turbulence intensity取值0.052%,turbulent viscosity ratio取值0.009,空间离散算法的相关参数都选择二阶迎风型。翼型外流场远场距离为12 m,攻角分别为0°、10°和15°时的数值仿真结果如下:(1)对钝后缘,攻角为0°,Cd=0.008 060 052,Cl=0;攻角为10°,Cd=0.014 627 732,Cl=1.062 077 3;攻角为15°,Cd=0.026 229 661,Cl=1.485 931 8。(2)对尖后缘,攻角为0°,Cd=0.007 993 417,Cl= 0;攻角为10°,Cd=0.014 367 92,Cl=1.054 641 4;攻角为15°,Cd=0.025 656 593,Cl=1.478 501 9。
翼型外流场远场距离为16 m,攻角分别为0°、10°和15°时的数值仿真结果如下:(1)对钝后缘,攻角为0°,Cd=0.008 072 766,Cl=0;攻角为10°,Cd=0.014 215 899,Cl=1.067 466 4;攻角为15°,Cd=0.025 651 792,Cl=1.488 497 1。(2)对尖后缘,攻角为0°,Cd=0.008 016 159 6,Cl=0;攻角为10°,Cd=0.014 027 672,Cl=1.057 444 5;攻角为15°,Cd=0.025 418 779,Cl=1.474 850 7。
翼型外流场远场距离为20 m,攻角分别为0°、10°和15°时的数值仿真结果如下:(1)对钝后缘,攻角为0°,Cd= 0.008 195 486,Cl=0;攻角为10°,Cd= 0.013 888 95,Cl=1.063 285 3;攻角为15°,Cd=0.024 878 235,Cl=1.487 204 1。(2)对尖后缘,攻角为0°,Cd=0.007 992 934,Cl=0;攻角为10°,Cd=0.013 878 605,Cl=1.056 018 2;攻角为15°,Cd=0.026 274 862,Cl=1.457 931。
3 仿真结果分析
3.1 湍流模型
采用Spalart-Allmaras湍流模型如图3(a)所示,12 m/16 m/20 m的远场距离+钝后缘/尖后缘的翼型配置在不同攻角条件下对Cl的仿真效果均较好,误差率最大不超过2%。20 m远场距离+钝后缘翼型配置对Cd的仿真效果最好,误差率最大不超过24%。比较不同参数配置下Cd和Cl误差率的均值和方差,钝后缘翼型+20 m远场距离的Cd误差率数值最佳,是(0.126 868 385,0.013 330 791),尖后缘翼型+16 m远场距离的Cl误差率数值最佳,是(0.001 681 592,1.756 76 × 10-6)。考虑到Cd误差率量级大于Cl误差率,钝后缘翼型+20 m远场距离的仿真效果最接近真实情况, 在0°、10°和15°攻角下的系数误差率分别是(0.84%,0.00%)、(13.31%,0.74%)、(23.91%,1.07%),仿真效果最接近真实情况。采用SST K-ω湍流模型如图3(b)所示,12 m/16 m/20 m的远场距离+钝后缘/尖后缘的翼型配置在不同攻角条件下对Cl的仿真效果均较好,误差率最大不超过4%。20 m远场距离+钝后缘翼型配置对Cd的仿真效果最好,误差率最大不超过31%。比较不同参数配置下Cd和Cl误差率的均值和方差,结合Cd误差率量级大于Cl误差率,钝后缘+20 m远场距离的误差率数值相对最佳,在0°、10°和15°攻角下的系数误差率分别是(1.30%,0.00%)、(15.65%,0.69%)、(30.94%,1.70%),仿真效果最接近真实情况。
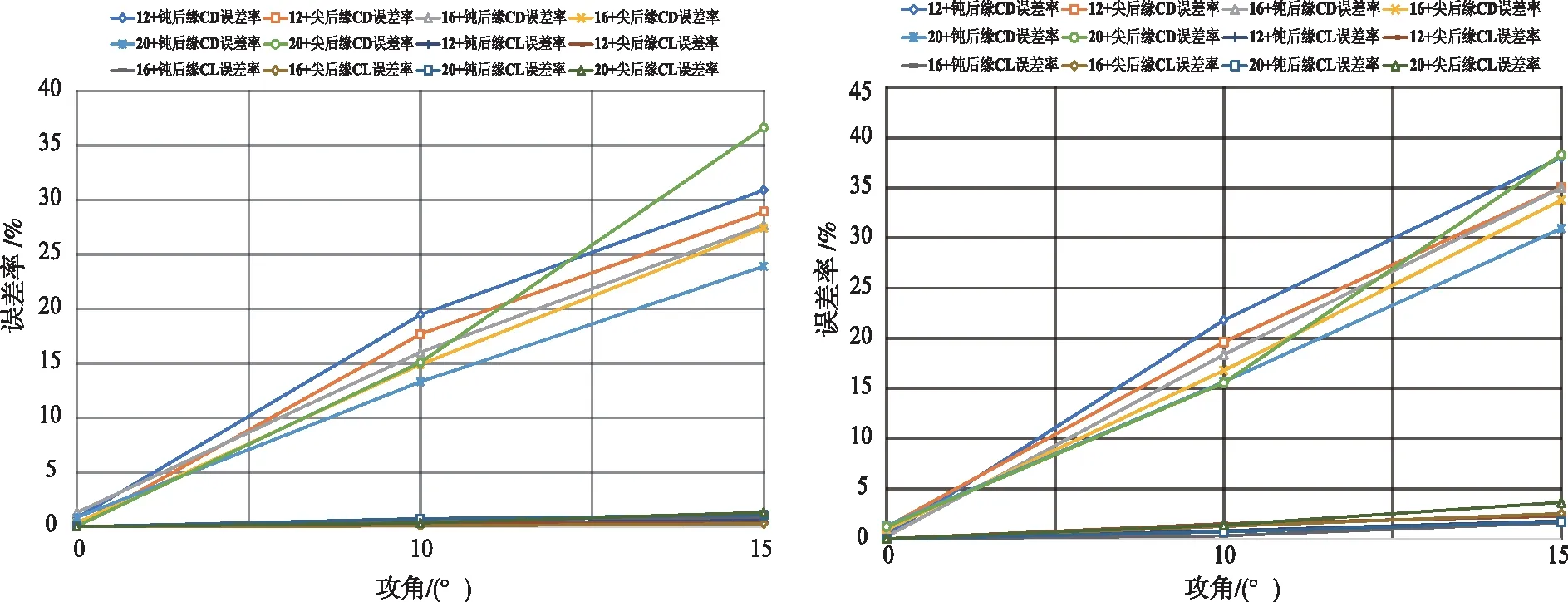
(a)Spalart-Allmaras模型 (b)SST K-ω模型
3.2 翼型后缘
采用钝后缘翼型如图4(a)所示,12 m/16 m/20 m的远场距离+SA/SST K-ω湍流模型配置在不同攻角条件下对Cl的仿真效果均较好,误差率最大不超过2%。20 m远场距离+SA湍流模型配置对Cd的仿真效果最好,误差率最大不超过24%。比较不同参数配置下Cd和Cl误差率的均值和方差,结合Cd误差率量级大于Cl误差率,SA湍流模型+20 m远场距离的误差率数值相对最佳,在0°、10°和15°攻角下的误差率分别是(0.84%,0.00%)、(13.31%,0.74%)、(23.91%,1.07%),仿真效果最接近真实情况。采用尖后缘翼型如图4(b)所示,12 m/16 m/20 m的远场距离+SA/SST K-ω湍流模型配置在不同攻角条件下对Cl的仿真效果均较好,误差率最大不超过4%。16 m远场距离+SA模型配置对Cd的仿真效果最好,误差率最大不超过28%。比较不同参数配置下Cd和Cl误差率的均值和方差,结合Cd误差率量级大于Cl误差率,SA湍流模型+16 m远场距离的误差率数值相对最佳,在0°、10°和15°攻角下的误差率分别是(0.34%,0.00%)、(14.90%,0.07%)、(27.42%,0.26%),仿真效果最接近真实情况。

(a)钝后缘 (b)尖后缘
3.3 远场距离
不同远场距离下数值仿真误差率如图5所示。在12 m的远场距离下,钝后缘/尖后缘翼型+SA/SST K-ω湍流模型配置在不同攻角条件下对Cl的仿真效果均较好,误差率最大不超过2%。尖后缘翼型+SA湍流模型配置对Cd的仿真效果最好,误差率最大不超过29%。比较不同参数配置下Cd和Cl误差率的均值和方差,尖后缘翼型+SA湍流模型的误差率数值相对最佳,在0°、10°和15°攻角下的数值分别是(0.05%,0.00%)、(17.67%,0.34%)、(28.94%,0.36%),仿真效果最接近试验数据。在16 m的远场距离下,钝后缘/尖后缘翼型+SA/SST K-ω湍流模型配置在不同攻角条件下对Cl的仿真效果均较好,误差率最大不超过3%。尖后缘翼型+SA湍流模型配置对Cd的仿真效果最好,误差率最大不超过28%。比较不同参数配置下Cd和Cl误差率的均值和方差,钝后缘翼型+SA与尖后缘翼型+SA的Cd误差率均值方差接近,分别是(0.150 021 789,0.017 470 786)和(0.142 171 489,0.018 363 59)。尖后缘翼型+SA的Cl误差率均值方差最小,为(0.001 681 592,1.756 76 × 10-6),所以尖后缘翼型+SA的仿真效果最接近试验数据,在0°、10°和15°攻角下的误差率分别是(0.34%,0.00%)、(14.90%,0.07%)、(27.42%,0.26%)。如图5(c)所示,在20 m的远场距离下,钝后缘/尖后缘翼型+SA/SST K-ω湍流模型配置在不同攻角条件下对Cl的仿真效果均较好,误差率最大不超过4%。钝后缘翼型+SA湍流模型配置对Cd的仿真效果最好,误差率最大不超过24%。比较不同参数配置下Cd和Cl误差率的均值和方差,钝后缘翼型+SA湍流模型的数值最小,在0°、10°和15°攻角下的误差率分别是(0.84%,0.00%)、(13.31%,0.74%)、(23.91%,1.07%),仿真效果最接近试验数据。
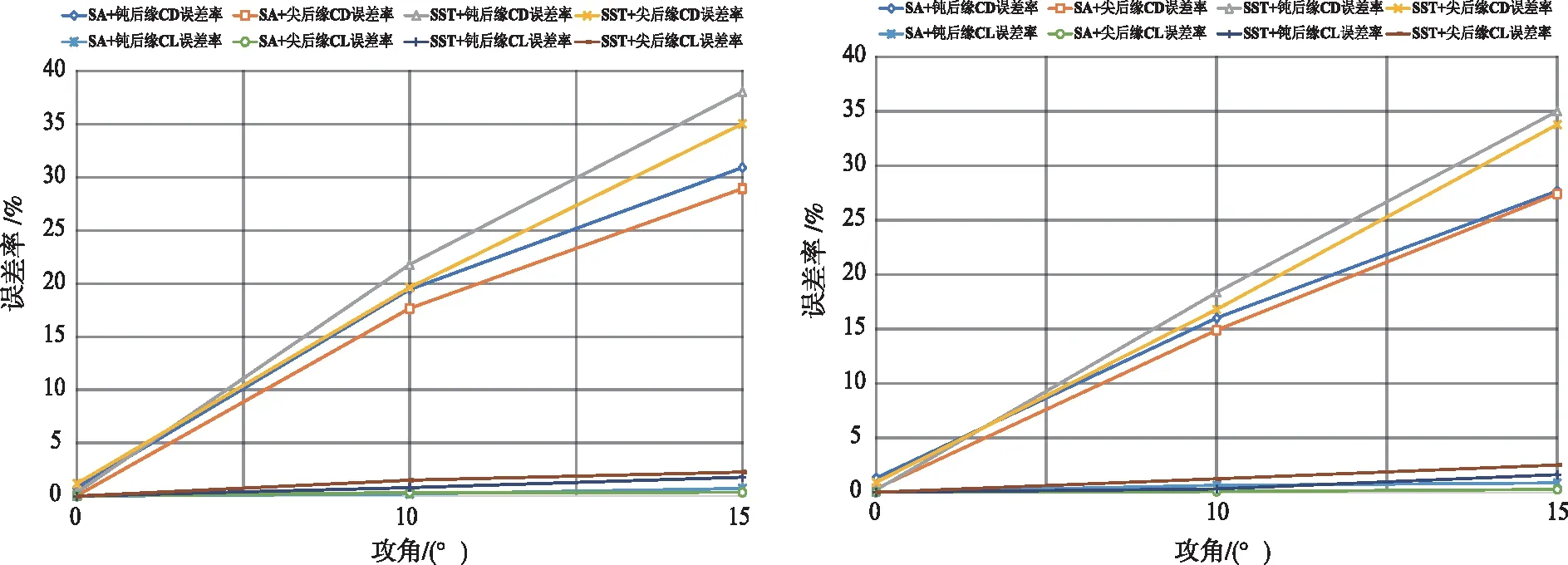
(a)12 m (b)16 m

(c)20 m
综上所述,从湍流模型的角度出发Spalart-Allmaras的表现优于SST K-ω。从不同翼型后缘形状的选择出发,翼型形状对仿真数值有明显影响。钝后缘翼型的数值仿真效果随着远场距离的增大而变好,尖后缘翼型的数值仿真效果先随着远场距离的增大变好,达到一个峰值(本文是16 m)后再随着距离的增大变差。从不同远场距离的选择出发,在距离相对较小时,仿真误差率相对较大,尖后缘的仿真效果优于钝后缘。随着距离的增大,误差率降低,尖后缘和钝后缘的仿真效果逐渐接近,达到某个数值(本文是20 m)后钝后缘的仿真效果优于尖后缘。
4 结 语
对NACA0012翼型,分析了在攻角为0°、10°和15°条件下不同后缘形状、远场距离和湍流模型对翼型外流场Cd和Cl的数值仿真结果的影响,有如下结论:
(1)优先考虑使用Spalart-Allmaras湍流模型。
(2)翼型形状对仿真效果的影响随着远场距离的变化而变化,远场距离较小时尖后缘仿真效果优于钝后缘。所以在绘制翼型外流场时,如果远场距离较小,那么要保证后缘形状尽量准确。但是如果远场距离较大,对后缘形状准确度的要求可以降低。远场距离的增大虽然会导致网格质量指标aspect ratio增大,但只要能控制在合理的范围内(本文是5 000),随着远场距离的增大,误差率可进一步降低。综合来看,在20倍的远场距离下采用Spalart-Allmaras湍流模型+钝后缘翼型可获得相对最佳的数值仿真结果,相应的误差率分别是(0.84%,0.00%)、(13.31%,0.74%)和(23.91%,1.07%)。

