预应力混凝土简支T梁桥荷载试验

徐 艳， 谭红梅， 曾 勇， 魏 星， 范和平， 罗小清

(1.重庆交通大学 山区桥梁与隧道工程国家重点实验室， 重庆 400074；2.重庆交通大学 山区桥梁结构与材料教育部工程研究中心， 重庆 400074；3.中交第二航务工程局有限公司投资事业部， 重庆 400074；4.忠县畅达建设投资有限公司， 重庆 404100)

简支T梁桥结构受力明确，容易实现工厂预制化，施工工期短，节约成本，在我国的公路建设中得到了大范围应用。为了确保简支T桥梁设计的合理性和安全性，必须对其承受荷载的能力进行检验。桥梁静载试验能够查验主梁受力情况以及承受荷载的能力是否满足规范规定的要求[1]，评价结果较为客观、准确，被业界人士广泛应用。严庆华等[1]模拟了某预应力混凝土T梁桥在实验荷载作用下的实际工作情况，检验了桥的强度、刚度等基本属性，并将试验得出的实际值与理论数值加以比较，判断实际承载能力是否符合要求。穆智峰[2]通过荷载试验对进行加固后的预应力混凝土简支T梁开展安全性能的评定，用有限元分析软件Midas Civil进行建模分析，将理论值与实际值进行对比，对结构进行安全评估。

本文以某预应力混凝土简支T梁为试验对象，开展荷载试验。检测两种不同荷载工况条件下控制截面的最大挠度变形值、应力和应变值并与设计值进行对比，使用有限元分析软件Midas civil进行建模，得出的最大弯矩值以及最大剪力值与规范进行分析对比，为同类桥梁检测提供了实践经验。

1 工程概况

某6 m × 30 m预制预应力混凝土连续T梁桥，桥梁总长为190 m，宽度为14 m；横断面布置：1.75 m(人行道及栏杆)+ 10.5 m(行车道)+ 1.75 m(人行道及栏杆)，下部结构形式为柱式墩和钻孔桩基础；0号桥台采用重力式U型桥台+承台桩基础，6号桥台采用重力式U型桥台+明挖扩大基础。桥面铺装为9 cm厚沥青混凝土，8 cm厚C50混凝土现浇层，桥梁伸缩缝采用CD-80型伸缩缝。设计荷载等级为公路二级，结构安全等级为一级，汽车荷载为公路-I级，人群荷载3.0 kN/m2。

2 静力荷载试验

2.1 测试工况

依据相关规范标准的规定，按桥梁的受力与变形特点，拟定静载试验工况如表1所示。

表1 静载试验工况

2.2 理论分析

采用Midas Civil进行模拟、计算分析。计算时，用梁单元模拟空心板，计算控制断面内力和位移。桥梁计算模型依据实际图纸尺寸建立等比例模型，材料强度取值于相应规范规定。有限元分析模型如图1所示。

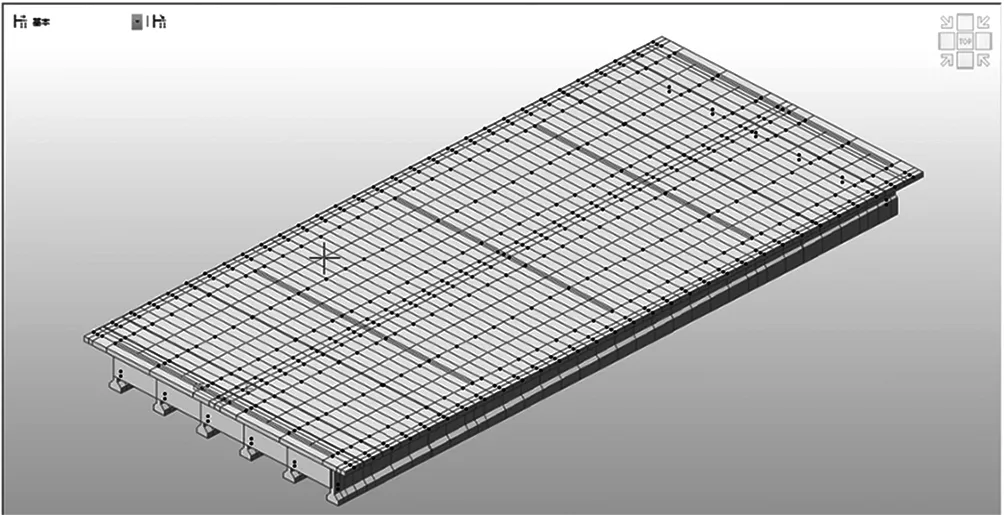
图1 有限元分析模型

2.3 测试方法

1)挠度数据采用塔尺测量数值。本次荷载试验共布置1个测试截面，位于跨中，该截面横向共设置5个挠度测点。

2)应力(应变)采用应变片和静态应变仪进行测量，分辨率为±1×10-6。在测试截面的表面上布置应变测点的位置，应力值由材料弹性模量换算而来，本次试验共布置1个测试截面，近偏载工况侧3片T梁设置有2个应变测点，其余每片T梁设置有1个应变测点。

2.4 测点布置

2.4.1 静力挠度测点

跨中布置挠度测试截面，横向有4个挠度测点，并采用塔尺进行测量，测点分别布置在各T梁横向跨中顶部，挠度测点平面具体布置如图2所示，挠度测点立面具体布置如图3所示。

图2 挠度测试点平面布置图

图3 挠度测试点立面布置图

2.4.2 静力应变测点

本桥共布置1个应变(应力)测试截面，取该截面编号为J1，截面应变测点分布在T梁底面及侧面。测试断面的每片主梁均需要贴片，每片T梁的测点需要2个应变片进行测量，传感器中心到T梁侧面距离为150 mm。根据该桥梁本身的结构特点，控制该截面静力应变测点具体布置如图4所示。

图4 J1截面静应变测试点布置图

2.5 荷载布置

为了确定加载车辆的型号、数量及质量等基本相关参数，须对结构进行分析、对荷载等效计算结果进行确认。

试验车型示意图如图5所示，加载车规格如表2所示，不同工况下车辆加载位置示意图如图6和图7所示。在荷载试验开始前，全部加载车都要检验并检查质量等基本指标，根据试验所需加载车辆的实际质量进行编组分类，确定不同加载工况时车辆的加载位置，保证试验开始至结束时所得出的荷载效率在合理的范围之中。

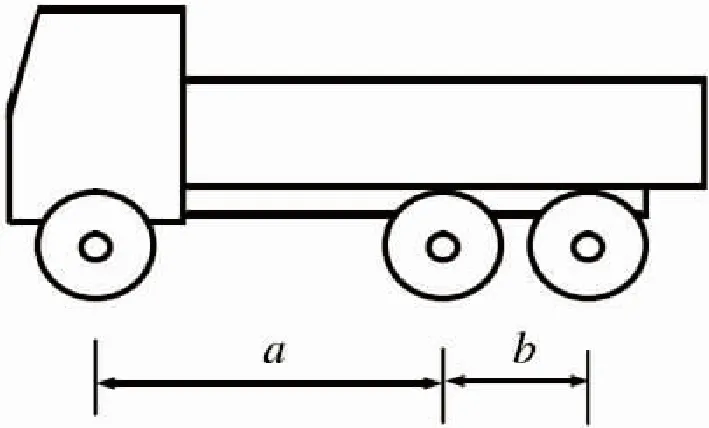
图5 车型示意图

表2 加载车规格

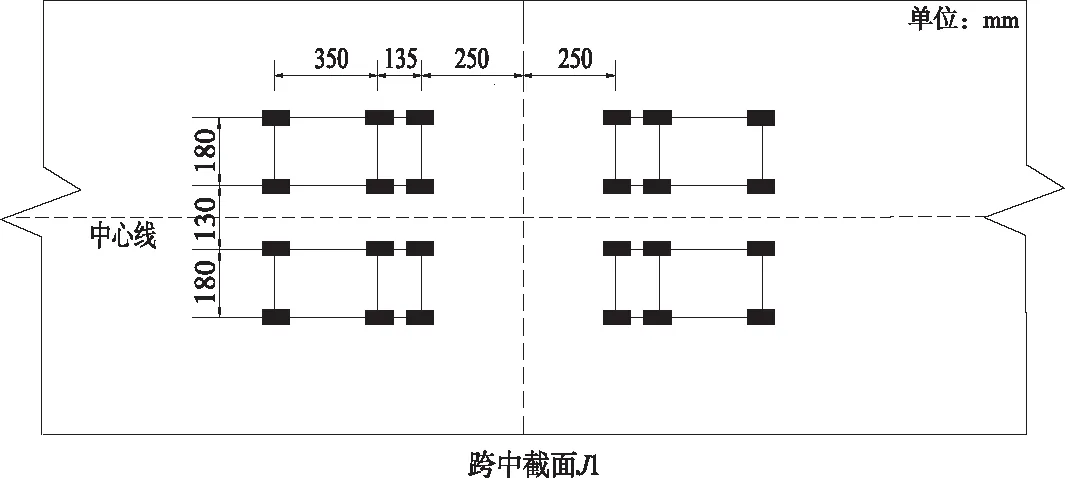
图6 工况1车辆加载位置示意图

图7 工况2车辆加载位置示意图

2.6 试验荷载效率

本试验的荷载为载重汽车，车辆数量的确定由式(1)等效换算而得[7]。对于该桥而言，各截面的弯矩值由设计荷载初步确定，并依此进行荷载的设计。本桥各试验截面的内力值以及荷载效率如表3所示。

(1)

式中：η是静力试验荷载效率；Sstate是检验项目在加载下的计算效应值；S是设计荷载作用下的最不利计算效应值；μ是根据规范采用的冲击系数。

表3 荷载效率计算结果

3 试验结果

3.1 挠度测试结果

在静载作用下，2种不同工况的实测最大挠度变形值与计算值的对比如图8和图9所示。

图8 工况1上、下游侧挠度实测值与计算值对比

从实测桥跨挠曲线与理论挠曲线对比可以看出，实测桥跨挠曲变形规律与计算值相符，且主要测试点的测量数值均小于理论计算值，说明该桥跨结构的实际整体变形情况合理。

图9 工况2上、下游侧挠度实测值与计算值对比

3.2 应力测试结果

在试验加载中，该桥各个测试截面的实测应变数值与理论计算应变数值的比较如表4和表5所示。表中负号表示应力受压。

表4 工况1应变实际测量值与计算值的比较

表5 工况2应变实际测量值与计算值的比较

在静载作用下，2种工况的实测最大应变变形值与计算值的对比如图10和图11所示。

图10 工况1上、下游侧应变实测值与计算值对比

图11 工况2上、下游侧应变实测值与计算值对比

在不同试验加载条件后，J1截面各测试空心底板的应力实际测试值与计算值的变化规律大致相似，校验系数和相对残余应变也都在合理的范围之内。

3.3 承载能力验算

根据规定，该类桥梁承载能力验算判别式如下：

γ0S≤R(fd,ξeadc,ξsads)Z2(1-ξc)

式中：γ0为结构的重要性系数；S为荷载效应系数；R(.)为抗力效应函数；fd为材料强度设计值;adc为构件混凝土几何参数值；ads为构件钢筋几何参数值；Z2为承载能力验算系数；ξe为承载能力恶化系数；ξc为配筋混凝土的截面折减系数；ξs为钢筋的截面折减系数。

3.3.1 抗弯承载力验算

利用有限元模型，算出T梁的恒载、活载内力。根据规范，采用荷载组合Ⅰ(1.2恒载+1.4汽车荷载+0.8人群荷载)的弯矩包络图如图12所示。

图12 弯矩包络图

利用计算的内力结果对跨中截面的抗弯承载力进行验算，考虑各折减系数。主梁的最大弯矩与折减后的截面抗力对比如下表6所示。

表6 抗弯承载能力验算

3.3.2 抗剪承载力验算

利用有限元模型，算出T梁的恒载、活载内力数值。根据规范，采用荷载组合Ⅰ(1.2恒载+1.4汽车荷载+0.8人群荷载)的剪力包络图如图13所示。

图13 剪力包络图

利用计算结果对跨中截面的抗弯承载力进行比较，取各折减系数。主梁的最大剪力与折减后的截面抗力对比如表7所示。

表7 抗剪承载能力验算

从以上检测结果可以得出结论，本桥的承载能力符合设计荷载标准(公路-Ⅰ级)的要求。

4 检测结果分析

为便于直观地分析比较，将相应桥跨的挠度检测结果如表8所示。

表8 挠度检测结果汇总

由表8可得，在2种不同荷载条件中，控制截面的实际挠度数值小于计算值，J1截面挠度校验系数介于0.64～0.87，属于规定的合理范围之内；J1截面最大挠度变化量为10.27 mm，近似于中跨跨径的1/2 921；当各个工况卸载时，控制测点的实时观测相对残余变形数值比规范限值更小，最大达到8.51%。

该试验结果显示，本次结构刚度符合规范的设计标准。

5 结 语

(1)在试验荷载条件时，主要控制截面实际测量的最大挠度、应变变形值小于理论计算值，在规定的合理范围之内。当卸载之后，各测点实际测量的相对残余变形数值都处于规范限制之内。主桥桥跨结构挠曲线走势光滑连续，与理论计算得到的曲线形状状况基本相一致，说明此桥整体工作性能良好，结构刚度满足规范要求。

(2)在试验荷载条件下，桥跨结构的主要测试截面实际测量得到的应力值在正常范围之内，结构实际强度达到规范所需要求。

(3)通过运用Midas Civil的相关计算，该桥所具有的抗弯承载力和抗剪承载力均满足当今设计荷载标准规定。

综上所述，该桥处于正常受力情况之内，该结构的刚度、强度等指标均符合规范要求，此荷载试验的研究方法和方式可为其他类型桥梁提供参考价值。