探究转动惯量影响因素和角动量守恒的演示装置
何佳蕊 冯志芳 杨雯雁 张冰鑫 程智博
(北京化工大学数理学院 北京 100029)
任何一门学科的发展都不是单纯地依赖原有理论的传播与推导,更需要依靠科学研究者的大胆猜想和可靠有效的实验验证,它从本质上来说是实验的科学。无论什么样的物理学的理论与猜想都是以实验为基础的,且都要受到实验现象与相关数据的证实。对于大学生而言,角动量可以说是一个全新的物理概念,同时,角动量守恒定律也是自然界中一个非常普遍的规律[1]。在研究相关问题时,为了便于描述转动状态的物理量,引入了角动量。定轴转动刚体的角动量公式为M=Jβ,角动量的定义式是由J(转动惯量,标量)与β(角加速度,矢量)的乘积而来,故为矢量,其方向判断只需通过右手四指环绕转轴转动的方向,大拇指所指方向即为角动量方向。
在日常生活中处处存在着角动量守恒的问题,如星球自转、直升机螺旋桨的转动等。其实,早在以前我国先人对于该现象便有相关记录,但却无法解释。西汉末年,丁缓制造出被中香炉,其能让香料不会由于外界扰动而掉落。那么,为什么会出现这样的现象呢?我们通过角动量守恒定律的观点来看待此现象,在内部结构上,丁缓把香盂两支点垂直悬于水平轴内两圆环中,当内环处于水平位置时,香盂因自身重量不会左右倾斜翻倒,而外环可使香盂不会左右倾斜翻倒(两环轴孔要垂直)[1];处于水平位置时,初始时刻,香盂和圆环组成的系统是静止的,香盂因为自身重心发生变化而导致对两圆环产生不同的压力,是系统的内力,内力对系统不产生力矩作用,所以不改变系统的角动量。根据上述推论,可以知道,系统受到的合外力矩为零,故此系统的角动量守恒正是当代“陀螺仪”的制造原理[2],最终产生了香盂口始终朝上的奇妙现象。
虽然,角动量守恒的现象在日常常见,但是,对于如何通过实验和量化来验证该定律上却没有成熟的实验体系。目前,国内大多研究者只在理论上设计了一些理论上方便可行的仪器,而针对实际教育中的仪器却很少设计。换句话说,对于性能较高、成本较低、便于实现的验证角动量守恒仪几乎没有,这也就造成了在物理实验等教学开展相关实验的困难点。
本文针对此现状设计了一款多功能性角动量守恒仪,借助该定性演示装置,可以在很大程度上帮助学生理解和掌握该定理,同时,借此装置,实验者还可以探究影响转动惯量的因素。国内也有教授在相关理论和器材的基础上改进发明出一种自制角动量守恒演示仪,但存在演示效果只能靠人眼目测感受其中的变化而不能由设备数据直接验证定理的缺点。目前,市面上用于角动量教学的相关实验器材虽操作方便、数据精确,但缺失验证角动量守恒这一功能。基于以上多方面考量,在前人原有的实验基础上,将装置的某些方面进行简化处理,同时增加了光电门和橡皮筋,更方便实验者定量测量和计算,使实验结论更加明显、更有说服力。
1 原理介绍
经典力学中的三大基本守恒定律为动量守恒定律、机械能守恒定律和角动量守恒定律[3-4],其中,动量守恒定律与机械能守恒定律两个守恒定律在高中阶段教学中均作了详细系统的学习与可视化研究。但关于角动量及转动惯量概念、角动量定理及角动量守恒定律方面的可视化资源较少,除了少量用于定性观察的演示实验外,国内用于定量验证角动量守恒定律的实验仪器和方案还十分缺乏与不便。为了解决这一实验难题,提高教学质量,本小组研制了集验证角动量和测量转动惯量于一体的定恒仪。
角动量即是指物体到原点的位移与动量相关的物理量。在经典力学中,角动量被定义为物体到原点的位移(矢径)和其动量的叉积:
L=r×p=Jω
式中,r为该点相对于转轴或原点的位失,p为该点的动量。因此,质点的角动量L是一个矢量,它的方向垂直于r与p所在平面,满足右手螺旋定则,即角动量是矢量,且是轴矢量。
转动惯量即物体转动时惯性的量度,用字母J表示[5],转动惯量等于组成物体各质点的质量m与它们到转轴的垂直距离r平方的乘积之和,即:
显而易见,转动惯量不仅与整个物体的质量有关,而且与质量的分布及转轴的位置有关。对于转动惯量,有转动惯量越大,其转动状态越不容易改变。例如,机械中常利用具有巨大转动惯量的飞轮来使运转平稳[6]。
角动量定理即对于质点系对任一固定参考点的角动量对时间的微商等于作用于该质点系的诸外力对参考点的力矩的矢量和,即:
式中,Mi为该点所受的合力矩。对于刚体同时存在,刚体绕定轴转动时,作用于刚体的合外力矩等于刚体绕此定轴的角动量随时间的变化率,即可表示为:
则有:
角动量守恒定律即为如果物体所受合外力矩等于零,或者不受外力矩的作用,物体的角动量保持不变。因此,当系统绕固定轴转动时,如若所受合外力矩为0或无外力矩作用时,该转动轴的转动惯量J与转动角速度ω的乘积为常数,即:
Jω=C
式中,C为常量。本文设计的实验装置中,系统可绕定轴转动,通过人为施加冲量矩,给予橡皮筋一定的弹性势能,可以通过改变装置上轻杆上滑块到转轴的距离,从而改变系统的转动惯量[7],进而实现改变系统绕定轴转动的角速度。根据角动量守恒定律,系统转动惯量增大,则系统的转动角速度减小;系统转动惯量变小,则系统的转动角速度增加[8]。在使用此实验装置时,由于在人为施加冲量矩后不再对装置进行操控,因此,系统的角动量保持恒定[9]。
2 实验装置介绍
图1 是演示装置组装后的简图,它主要由铁架台和通过轴承与旋转装置相连的轻质杆和若干滑块组成。
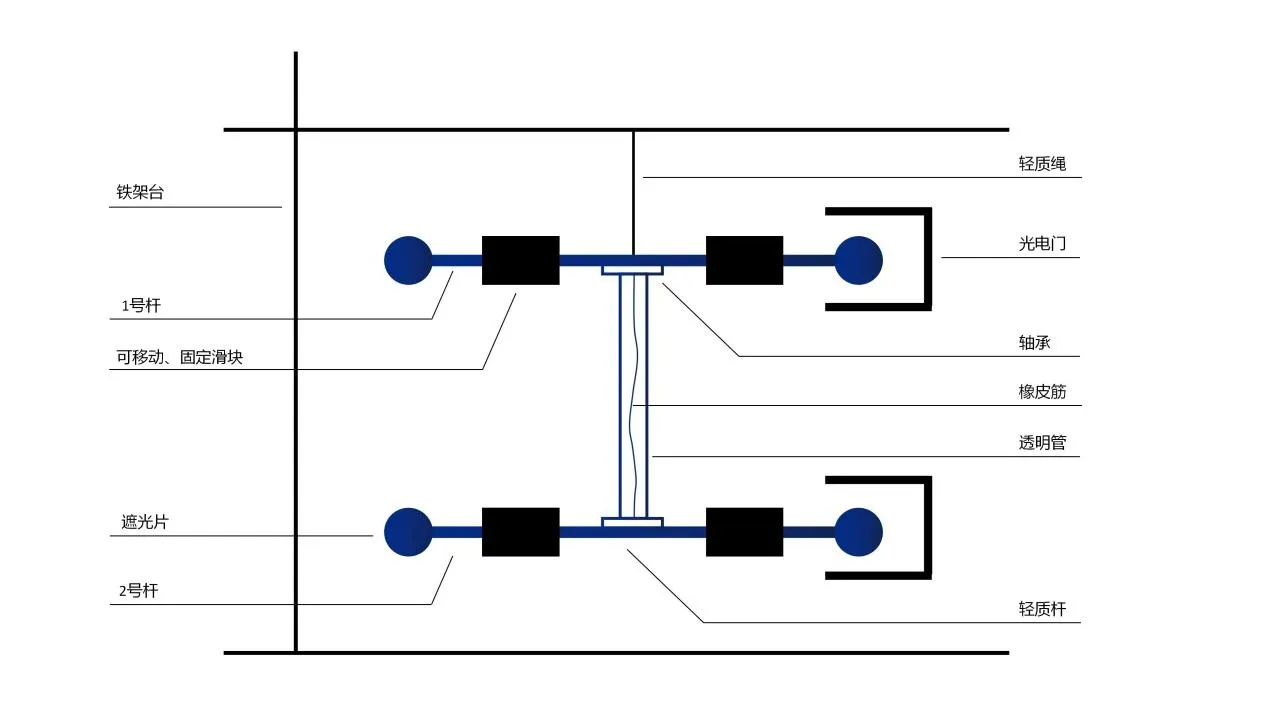
图1 实验装置设计图
本实验的材料有一个铁架台(起固定、支撑作用)、一根轻质绳(连接铁架台与旋转装置)、一根轻质橡皮筋(弹劲系数较大,给转动系统提供能量)、一根透明管(与橡皮筋共同连接上、下两根轻质杆)、两个轴承、两个相同的轻质杆(设上杆为1 号杆,下杆为2 号杆)、两个光电门(起计时作用)、8 个质量分布均匀的大小相同的滑块(其中4 个滑块完全相同,另外4 个滑块完全相同,但比前4 个滑块质量小)、4 个大小适中的遮光片。
加工方案:将8个滑块分别打孔,保证滑块上的孔洞直径略大于轻质杆的直径,能够让其在轻质杆上实现自由移动;在两根轻质杆中心处打孔,保证孔洞直径略小于轴承直径。
安装步骤:首先组装旋转装置,将已打好孔的其中4个滑块穿入轻质杆,将4个遮光片分别固定在轻质杆的两端,再将轴承嵌入轻质杆内,用橡皮筋把两个轻质杆相连,中间用透明管包裹橡皮筋,并把两个轴承连接在一起组成转动系统,最后,用轻质绳把转动系统连接在铁架台上,装置组装完成,可顺利进行实验操作。
实验装置优点如下:(1)通过铁架台的支撑作用,实现了转动系统的悬空,上、下两根轻质杆的转动现象进行对比,更加直观,且更易得出结论;(2)利用遮光片与光电门的结合,可在一定程度上进行简单的定量计算,使得实验结果更有说服力;(3)轻质橡皮筋的存在保证每次实验操作中转动相同的圈数,即可近似认为每次给系统提供的初始能量相同,以一种简便的方式即可实现控制变量。
3 实验过程
3.1 转动惯量影响因素实验
3.1.1 探究质量相对中心转轴分布的变化对转动惯量影响的实验
取4 个完全相同的滑块,如图1所示,分别将1 号轻质杆和2 号轻质杆上应的4 个滑块调整到对应相同的位置,且距离透明管所在中心轴的距离相同。此时,用手将1 号轻质杆固定,将2 号轻质杆沿顺时针(或逆时针)方向转动,转动10圈后即可停止。接下来,同时释放1 号、2 号两根轻质杆,即可观察到两根杆分别沿以透明管所在的直线为轴的顺时针和逆时针方向旋转,且转动的速度大致相同。通过两个光电门,分别测量两个轻质杆的转动周期T1、T2,根据T1、T2,即可计算出旋转数圈,进一步可以得到某相同时刻1 号杆、2 号杆两杆的角速度ω11、ω21。
再将上、下4 个滑块向靠近透明管的方向移动相同距离(见图2),并且保证上、下两对对应的滑块在一条竖直线上,重复上述操作,记录与之前释放后转动相同圈数时刻的角动量(目的是确保系统获得的转动动能相同),此时,即可发现1 号、2 号两个轻质杆的ω21、ω22较之前增大。当将上、下4 个滑块向远离透明管的方向移动相同距离(见图3,保证4 个滑块离装置中央透明杆的距离较图1 的距离更大),重复上述操作,记录并求得与之前释放后转动相同圈数时刻的角动量,此时,即可发现1 号、2 号两个轻质杆的角速度ω31、ω32较之前减小。
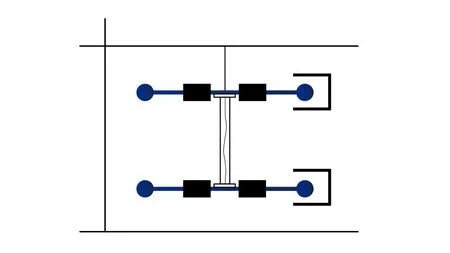
图2 实验演示图A

图3 实验演示图B
根据上述实验结果及下列能量守恒公式:EK=,可得出如下结论:当系统的转动动能相同时,ω越小,J越大,反之亦然。因而,当1号轻质杆、2号轻质杆两部分质量相同时,滑块的质量相对于中心转轴分布越近,转动惯量越小;当滑块质量相对于中心转轴分布越远,转动惯量越大。
3.1.2 探究质量大小对转动惯量影响的实验
在实验(1)的基础上,更换原有4 个滑块为另外4个质量相同但与实验(1)的4 个滑块质量不同的滑块(见图4),置于与第一次实验的相同位置,此时,重复以往实验操作(用手固定1 号的轻质杆,将2 号的轻质杆沿顺时针或逆时针方向转动,转动10 圈后即可停止,同时释放1号、2号两根轻质杆,即可观察到两根杆分别沿以透明管所在的直线为轴的顺时针和逆时针方向旋转,且转动的速度大致相同),记录并求得与之前释放后转动相同圈数时刻(为了确保系统获得的转动动能相同)的角动量,即可发现此时的ω41、ω42相比于第一次实验的ω11、ω21减小。
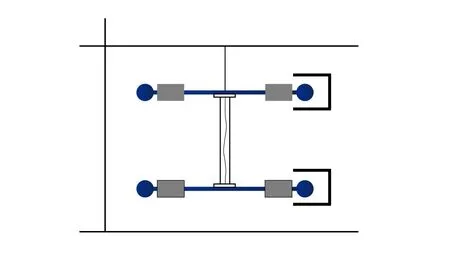
图4 演示装置图C
根据上述实验结果及下列能量守恒公式:EK=,可得出如下结论:当系统的转动动能相同,ω越小,J越大,反之亦然。因而,1号轻质杆、2号轻质杆两端的滑块与中心转轴的距离相同时,滑块质量越大,转动惯量越大;滑块质量越小,转动惯量越小。
3.2 角动量守恒实验
(1)演示转动惯量相同的1 号轻质杆、2 号轻质杆两部分,当系统合外力矩为0 时,在内力矩作用下,两轻质杆分别以等大反向的角速度转动的现象。
取4 个完全相同的滑块,如图1所示,分别将1 号轻质杆、2 号轻质杆上分别对应的两个滑块调整到距离透明管所在中心轴距离相同的位置,重复上述实验操作(用手固定1 号的轻质杆,将2 号的轻质杆沿顺时针或逆时针方向转动,转动10 圈后即可停止,同时释放1 号、2 号两根轻质杆,即可观察到两根杆分别沿以透明管所在的直线为轴的顺时针和逆时针方向旋转)。通过上、下两个光电门,分别测量两个轻质杆的不同时刻的转动周期T1、T2,可计算出旋转数圈,进而得到在某相同时刻1 号轻质杆与2 号轻质杆两杆的角速度分别为ω1、ω2,可以得到ω1大小等于或近似等于ω2,即可得到J1ω1+J2ω2= 0,其中,J1=J2。
(2)演示转动惯量不同的1 号轻质杆、2 轻质号杆两部分,当系统合外力矩为0 时,在内力矩作用下,分别以不同的角速度沿相反方向转动的现象。
如图5所示,将1 号轻质杆、2 号轻质杆上分别对应的两个滑块调整到距透明管所在中心轴不同的两个位置(该放置滑块的方式可以实现上、下两杆的转动惯量不同),但须保证1 号轻质杆和2 号轻质杆上分别对应的两个滑块距离透明管所在中心轴的位置相同(即保证上、下两根轻质杆与4 个滑块组成的部分系统关于透明管所在的中心轴对称),重复上述实验操作(用手固定1号的轻质杆,将2号的轻质杆沿顺时针或逆时针方向转动,转动10 圈后即可停止,同时释放1 号、2号两根轻质杆,即可观察到两根杆分别沿以透明管所在的直线为轴的顺时针和逆时针方向旋转)。通过上、下两个光电门,分别测量两个轻质杆的转动周期T1、T2,即可计算出某相同时刻上、下两杆的角速度ω1、ω2[10],可得ω1<ω2。

图5 演示装置图D
上述实验现象清楚明了地反映了角动量守恒这一基本物理规律,因为保证了在释放上、下两根轻质杆前系统静止,所以,系统的总角动量为零。在释放后,仅在内力矩的作用下实现转动,并无其他的外力矩作用在该系统上,其角动量总和也应为零,即,当满足J1>J2(或J1<J2)的条件时,ω1<-ω2(或ω1>-ω2)。
4 结论
通过以上的实验操作,可以得到以下结论。
(1)在物体质量相对转轴分布相同时,重物的质量越大,系统的转动惯量越大,反之亦然。在物体质量相同的情况下,物体质量相对转轴分布越近,转动惯量越小;当物体质量相对转轴分布越远,转动惯量越大。
(2)在保证系统所受合力矩为零的条件下,系统在内力矩的作用下转动,其角动量守恒。
根据角动量的现有知识,本文设计了一个可用于同时探究转动惯量影响因素及角动量守恒定律演示的转动装置。在演示过程中,通过改变滑块质量和滑块质量分布相对转轴的关系,从而改变转动系统的转动惯量,使转动系统的角速度发生显著变化,最后达到演示角动量守恒定律的目的。
该角动量守恒演示仪虽然使用了平面轴承,使装置旋转时所受的摩擦力矩在最大程度上减小,但仍不可能彻底将其消除。另外,空气阻力及轻质绳、橡皮筋之间存在的摩擦力形成的阻力矩也是必然存在的,所以会导致角动量有关现象呈现的时间较为短暂,演示效果并不能完全符合预期。利用光电门测量数据推算角速度也存在不可避免的系统误差角速度也存在不可避免的系统误差,使定量测量出的数据不能完全相等,但在系统误差允许范围内,测量数据依旧可以作为验证角动量守恒的依据。
本文设计的角动量守恒演示仪与传统的装置相比,优点也是显而易见的,其材料容易获得,同时组装起来也较为简单,操作原理便于理解,可以达到装置轻巧、操作简单、现象直观的目的。因此,该装置对于探究影响转动惯量因素及角动量守恒的演示是明显且可信的,反映的物理规律深刻且富有启发性。
与此同时,本实验演示装置能演示出多种与角动量定理相关的实验,能把刚体定点转动这个复杂而令人困惑的问题清晰地反映出来,从而可以运用在今后的课堂演示上,可先让学生预想实验现象,然后用该仪器进行实验,以检验他们的理解是否正确,最后用理论加以分析,达到应用的目的。

