复合材料尾翼壁板结构承载效率权衡分析
杜恒毅 梅杰 孙见卓 张洪峰 吴德财
(1.中国商飞上海飞机制造有限公司/复合材料中心 上海 200123;2.中国商飞北京民用飞机技术研究中心/民用飞机结构与复合材料北京市重点实验室 北京 102211)
1 背景
飞机结构设计是飞机总体设计的重要组成部分,统计表明,每单位飞机结构重量的降低,能够降低约4.525 单位的飞机总重[1]。在满足飞机气动性能要求的前提下,降低结构重量进而提高结构效率,成为未来民机产业技术发展的主要目标之一。复合材料密度小、比刚度高、比强度高、抗疲劳断裂性能好、耐腐蚀、便于整体成型,可以显著减轻结构件的重量[2],碳纤维增强复合材料重量仅为普通钢制材料的1/5,强度却可以达到它的10 倍[3]。大飞机的主承力结构件采用复合材料制造已成趋势。复合材料在飞机上的应用经历了前缘—口盖—整流罩—扰流板—升降舵—方向舵—襟副翼—垂尾—平尾—机身和机翼等主承力结构应用的过程,于20世纪80年代和20世纪90年代初应用于平尾和垂尾等主承力结构[4]。复合材料尾翼盒的主要承力构件有壁板、翼梁和翼肋,其中,壁板主要由蒙皮和长桁组成。复合材料整体壁板与铆接壁板相比,在保证相同的刚度/强度情况下,结构质量可减轻15%~20%[5];与蒙皮相比,复合材料壁板较金属壁板长桁减重比例更高,是因为长桁的铺层中0°比例很高,充分发挥了CFRP比弹性模量高的优势[6]。目前,复合材料尾翼加筋壁板主要以“T”型长桁壁板和“I”型长桁壁板为主,分别如图1(a)、图1(b)所示。“T”型长桁壁板结构相对简单,制造成本较低,空客A350 等系列尾翼壁板采用了“T”型长桁壁板结构;“I”型长桁壁板较“T”型长桁壁板结构更复杂,对制造工艺的要求更高,波音B787等系列尾翼采用了“I”型长桁壁板结构。

图1 “T”型、“I”型长桁
研究不同构型长桁对复合材料尾翼壁板承载效率的影响,具有重要的工程意义。本文主要对复合材料尾翼“T”型长桁和“I”型长桁加筋壁板结构承载效率进行了对比分析,权衡了“T”型长桁和“I”型长桁加筋壁板典型特征尺寸对承载效率的影响,为复合材料尾翼壁板结构选型提供一定的设计依据。
2 复合材料尾翼壁板承载能力理论算法
2.1 基本假设
先进复合材料的拉伸和压缩破坏应变超过10 000µε,而拉伸使用许用应变值一般可达6000µε,但压缩使用许用应变值只有2700µε左右,这主要是受到冲击压缩破坏曲线的门槛值所控制,由此可见,复合材料的压缩使用许用值明显偏低[7]。对于复合材料尾翼加筋壁板承载能力的考核一般包括拉伸、压缩两个方向,其中,壁板拉伸承载能力主要是通过拉伸应变来表征。考虑到复合材料拉伸许用应变值一般高于压缩许用应变值,当壁板压缩强度满足安全要求时,壁板拉伸强度一般也满足安全要求。因此,本文所论述的复合材料尾翼加筋壁板承载能力为压缩承载能力。
假设壁板结构仅在长桁轴线方向承受均匀轴压载荷,对于复合材料尾翼壁板结构,无论是“T”型长桁壁板还是“I”长桁壁板,在蒙皮/长桁刚度比满足一般设计要求的情况下,认为长桁间局部蒙皮的支持边界相似,蒙皮局部失稳临界载荷相同。
综上,本文中采用长桁—蒙皮组合剖面的柱强度表征尾翼加筋壁板承载能力,考虑不同长细比对壁板失效模式的影响。尾翼加筋壁板承载效率可由下式表示:
式中,η代表承载效率,P代表承载能力,m代表结构重量。
同时,为了分析各结构参数对结构效率的影响,结合工程实际,在复合材料经典层压板理论基本假设的基础上,补充以下3点假设:(1)假设复合材料层压板在厚度方向上均为对称均衡布置,不考虑横向剪切效应和拉剪、拉弯耦合效应;(2)假设长桁为等间距分布、剖面相同、面积相等、长桁与蒙皮材料相同;(3)假设壁板结构在变形协调下,蒙皮随长桁整体拉伸或压缩的变形量相同。
2.2 复合材料尾翼加筋壁板力学性能分析
根据经典层压板理论,层压板内力—应变本构关系为:
式中:{N}、{M}分别为层压板剖面单位长度上的力、力矩;{ε0}、{k}分别为层压板中面的应变、扭曲率;[A]、[B]、[D]矩阵分别为层压板的面内刚度矩阵、耦合刚度矩阵、弯曲刚度矩阵。
A、B、D矩阵中的刚度系数可按层压板铺层参数相关函数计算:
式中,N代表层压板的总层数,zk,zk-1分别代表第k层和第k-1层的z 坐标代表第k层铺层的偏轴模量。与铺层材料主方向的正轴模量2,6)和该铺层的铺层角有关。铺层材料主方向的正轴模量按下式计算:
式中:E11表示单向带沿纤维方向的弹性模量;E22表示单向带垂直于纤维方向的弹性模量;G12表示单向带的剪切弹性模量;ν12表示单向带的纵向泊松比;ν21表示单向带的横向泊松比。
结合复合材料铺层对称均衡假设,式中,Bij=0,A16=0,A26=0,可以得到复合材料层压板在长桁轴线方向等效弹性模量为:
层压板在垂直于长桁轴线方向的等效弹性模量为:
本文所使用的典型复合材料尾翼加筋壁板的材料力学性能[8]如表1所示。

表1 T800级复合材料单向带的力学性能
2.3 长桁—蒙皮组合剖面承载能力分析方法
复合材料尾翼加筋壁板一般为具有不稳定剖面的加筋板,其柱曲线如图2中曲线DEFC段表示[7]。按加筋壁板的有效长细比L′/ρ,将其破坏形式分为3 个区段。

图2 加筋平板的柱曲线
(1)在FC范围,属长柱区,加筋壁板以弯曲失稳形式破坏。在总体失稳之前,剖面不发生局部失稳,其临界应力用欧拉方程计算[7]:
式中:Exc表示加筋壁板的压缩弹性模量;L′表示加筋壁板有效长度,单位为mm,,L为加筋壁板的实际长度,C为端部支持系数。
(2)在DE范围,属压损区,加筋短板以局部失稳而破坏。将加筋壁板结构按特征离散成多个板元,板元压损应力采用半经验公式计算[9]:
加筋壁板的压损应力取各板元压损应力的加权平均值:
(3)在EF范围系过渡区(L′/ρ一般为20~60),加筋壁板以局部失稳和弯曲失稳混合形式破坏,其破坏应力采用半经验公式约翰逊—欧拉方程计算[7]:
式中:σcr表示加筋板的破坏应力;σcc表示加筋板的压损应力;Exc表示板元沿长桁轴向的压缩弹性模量;L′表示加筋壁板有效长度,单位为mm,L为加筋壁板的实际长度,C为端部支持系数;ρ表示剖面回转半径,I和A分别为加筋壁板剖面的惯性矩和面积。
另外,在计算加筋壁板柱强度时,应计入蒙皮的有效宽度。当蒙皮未失稳时,其有效宽度等于长桁之间的距离,而蒙皮失稳时,应力重新分布,长桁之间的蒙皮宽度上应力不均匀(见图3),蒙皮承受相当于长桁应力的有效宽度小于长桁间距。

图3 蒙皮失稳时应力分布图
按照本文的基本假设,对于蒙皮和长桁材料相同情况,蒙皮有效宽度为[7]:
式中,δ为蒙皮厚度。E为弹性模量。σst为桁条应力。
加筋壁板的柱强度计入有效蒙皮宽度的具体步骤如下:(1)计算单个筋条柱强度,即按本章所述方法计算长桁破坏应力;(2)算出蒙皮有效宽度,式中σst用(1)算出的应力;(3)按本章所述方法计算具有有效蒙皮的筋条柱强度,得出新的破坏应力;(4)重新计算蒙皮有效宽度,式中,σst用替换。
2.4 壁板结构特征及参数说明
本文综合考虑了复合材料尾翼壁板典型结构尺寸,对所有典型结构尺寸进行组合,取长桁/壁板刚度比在0.4~0.6的壁板构型进行承载效率的对比分析。
“I”型长桁壁板的尺寸参数示意图如图4所示,其中,t1代表长桁腹板厚度,t2代表长桁底缘厚度,t3代表长桁顶缘厚度,w1代表长桁腹板高度,w2代表长桁底缘宽度,w3代表长桁顶缘宽度。

图4 “I”型长桁尺寸参数示意图
“T”型长桁壁板的尺寸参数示意图如图5所示,其中,t4代表长桁底缘厚度,t5代表长桁腹板厚度,w4代表长桁底缘宽度,w5代表长桁腹板高度。
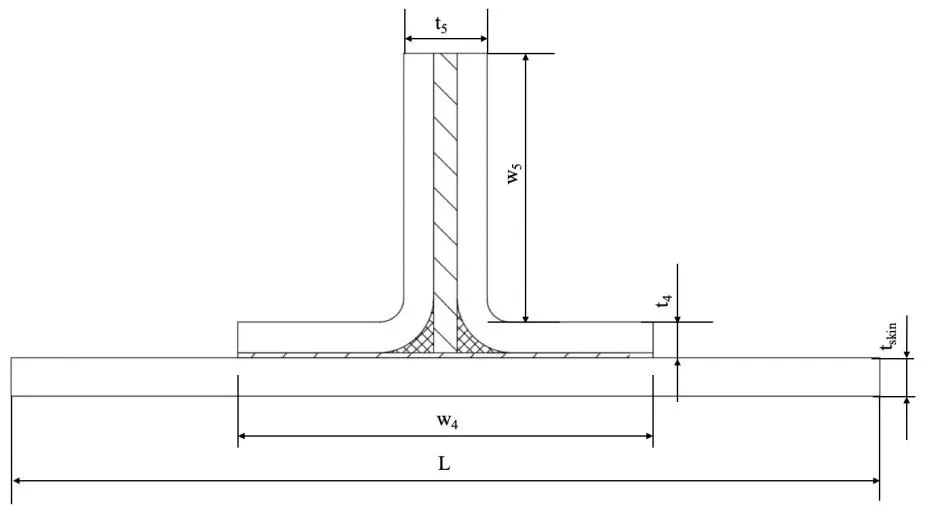
图5 “T”型长桁尺寸参数示意图
对于两种结构类型的长桁,均用tskin表示蒙皮厚度,wskin表示蒙皮宽度(长桁间距),L表示加筋板长度。其中,wskin和L参数大小为固定值。上述参数的取值范围见表2。
为了对比“T”型长桁结构和“I”型长桁结构对复合材料尾翼壁板承载效率的影响,我们首先按照表2所示典型尾翼壁板特征尺寸,遍历了所有结构形式加筋壁板的承载能力,计算出各个构型所对应的结构重量及其承载效率。取长桁/壁板刚度比在0.4~0.6 的壁板构型,以其结构重量为横坐标,承载效率为纵坐标,分别画出“T”型长桁与“I”型长桁加筋壁板的结构重量—承载效率散点图,通过散点图的分布状况,对比分析不同长桁构型对壁板承载效率的影响。
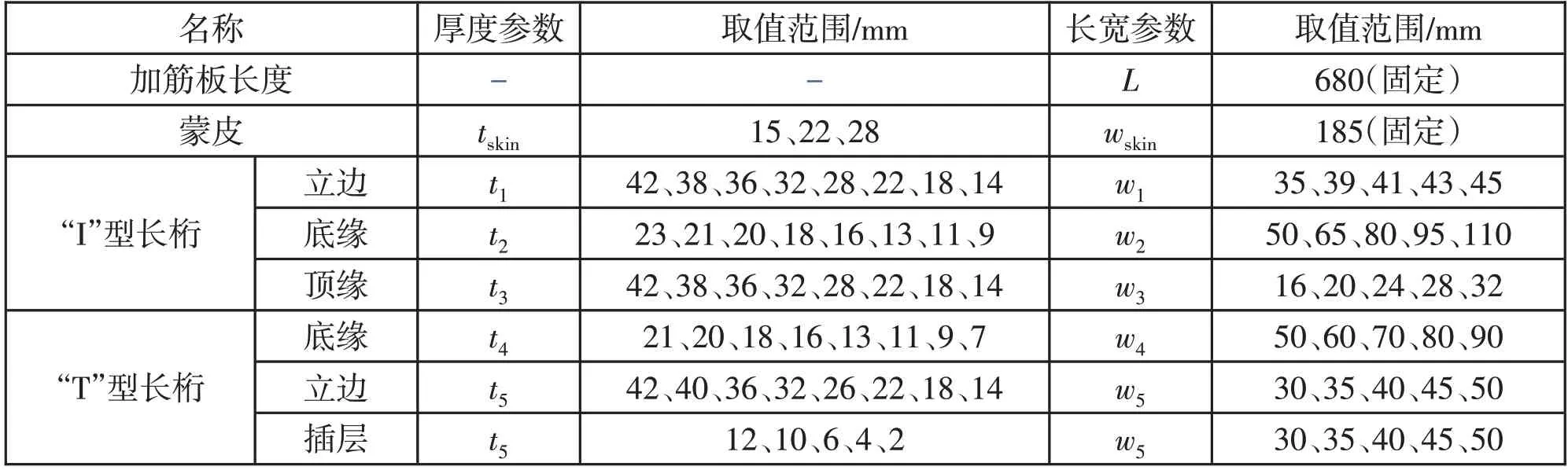
表2 典型壁板结构尺寸表
3 “I”型长桁壁板与“T”型长桁壁板结构效率对比
本文分别选取尾翼盒翼根区、中间区和翼梢区壁板作为研究区域,对比“I”型长桁加筋壁板与“T”型长桁加筋壁板的结构承载效率。
3.1 翼根区
选取尾翼盒段根部区域壁板作为研究对象,如图6(a)[10]部分所示,其中,翼根区典型蒙皮厚度特征按28层选取。

图6 尾翼壁板翼根区(a)、中间区(b)和翼梢区(c)
通过将数据输入专用计算工具(权衡分析思路如图7所示),画出长桁/壁板刚度比在0.4~0.6的“I”型长桁加筋壁板与“T”型长桁加筋壁板所有构型的结构重量—承载效率散点图,如图8所示。图中,“I”型长桁壁板数据用三角点表示,“T”型长桁壁板数据用圆点表示,图的横坐标为壁板的结构重量(g),纵坐标为其承载效率(N/g)。
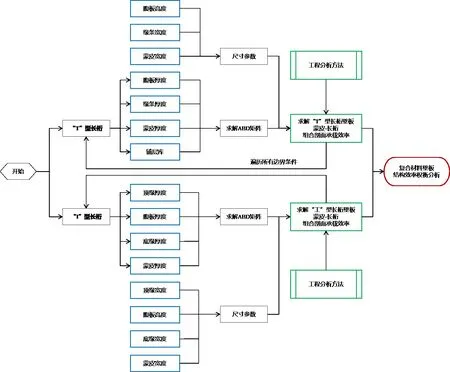
图7 “I”型长桁与“T”型长桁结构效率权衡思路
表3为“I”型长桁与“T”型长桁加筋壁板结构效率表。由于图8 中散点图的结构重量主要分布在1550~2000g 之间,考虑到中段数据的完整性,表3 分别选取了壁板结构重量为1650g、1750g、1850g 附近的数据进行对比分析,此时,“I”型长桁壁板与“T”型长桁壁板的最高结构承载效率之比分别为1.36、1.24 和1.19。因此,在复合材料尾翼壁板结构设计合理、承载效率相同的情况下,“I”型长桁壁板比“T”型长桁壁板在尾翼根部区域可减重约19%以上。

图8 翼根区“I”型长桁与“T”型长桁结构重量与承载效率散点图

表3 翼根区“I”型长桁与“T”型长桁加筋壁板结构效率表
3.2 中间区
选取尾翼盒段中间区域壁板作为研究对象,如图6(b)部分所示,其中,中间区蒙皮厚度特征取22层。
通过将数据输入所编写的工具,计算出了长桁/壁板刚度比在0.4~0.6 之间的“I”型长桁壁板与“T”型长桁壁板所有构型的结构重量—承载效率散点图,如图9所示。图中,“I”型长桁壁板数据用三角点表示,“T”型长桁壁板数据用圆点表示,图的横坐标为长桁壁板的结构重量(g),纵坐标为其承载效率(N/g)。
表4为“I”型长桁与“T”型长桁加筋壁板结构效率表。由于图9中散点图的结构重量主要分布在1250~1750g 之间,考虑到中段数据的完整性,表4 分别选取了壁板结构重量为1350g、1450g、1550g、1650g 附近的数据进行对比分析,此时,“I”型长桁壁板与“T”型长桁壁板的最高结构承载效率之比分别为1.52、1.43、1.30和1.15。因此,在复合材料尾翼壁板结构设计合理、承载效率相同的情况下,“I”型长桁壁板比“T”型长桁壁板在尾翼中部区域可减重约15%以上。
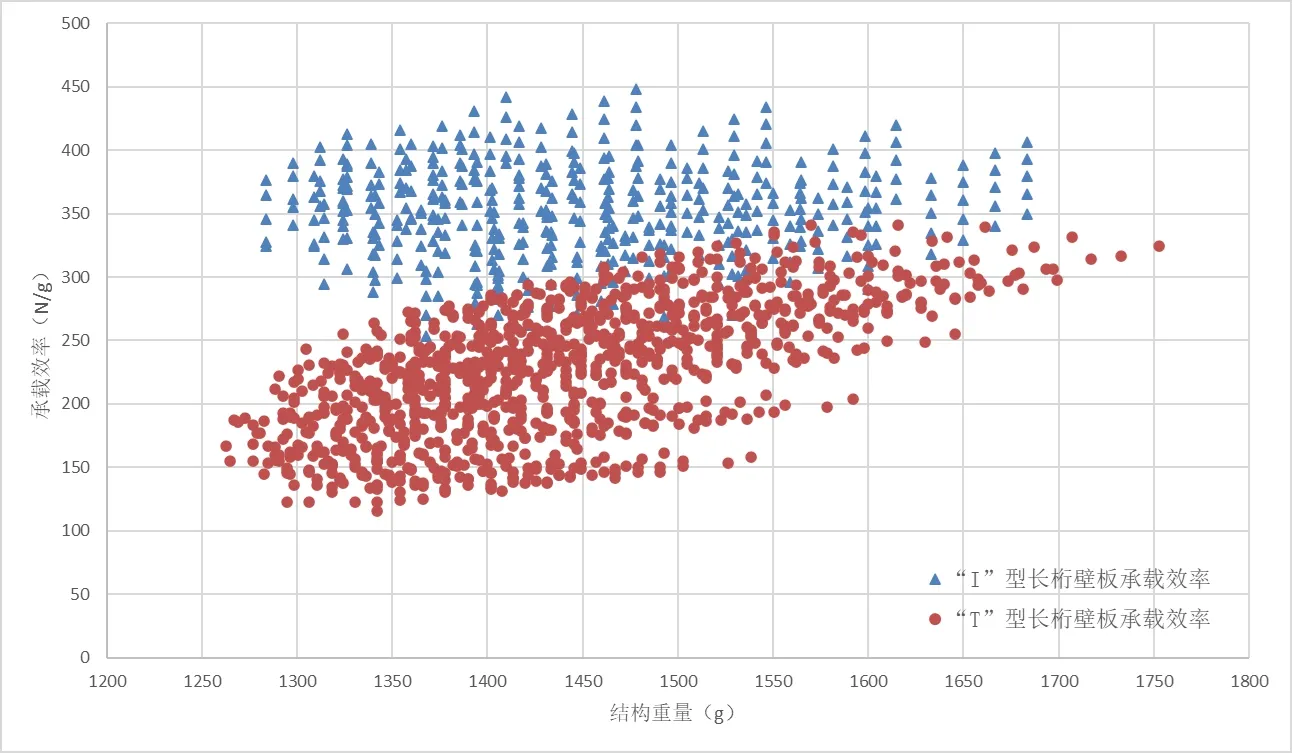
图9 中间区“I”型长桁与“T”型长桁结构重量与承载效率散点图

表4 中间区“I”型长桁与“T”型长桁加筋壁板结构效率表
3.3 翼稍区
选取尾翼盒段翼梢区壁板作为研究对象,如图6(c)部分所示,其中,翼根区蒙皮厚度特征取15层。
通过将数据输入所编写的工具,计算出了长桁/壁板刚度比在0.4~0.6 的“I”型长桁壁板与“T”型长桁壁板的结构重量与承载效率散点图,如图10所示。图中,“I”型长桁壁板数据用三角点表示,“T”型长桁壁板数据用圆点表示,图的横坐标为长桁壁板的结构重量(g),纵坐标为其承载效率(N/g)。
表5为“I”型长桁与“T”型长桁加筋壁板结构效率表。由于图10中散点图的结构重量主要分布在850~1350g 之间,考虑到中段数据的完整性,表5 分别选取了壁板结构重量为950g、1050g、1150g、1250g附近的数据进行对比分析,此时,“I”型长桁壁板与“T”型长桁壁板的最高结构承载效率之比分别为1.80、1.78、1.63 和1.37。因此,在复合材料尾翼壁板结构设计合理、承载效率相同的情况下,“I”型长桁壁板比“T”型长桁壁板在尾翼稍部区域可减重约37%以上。
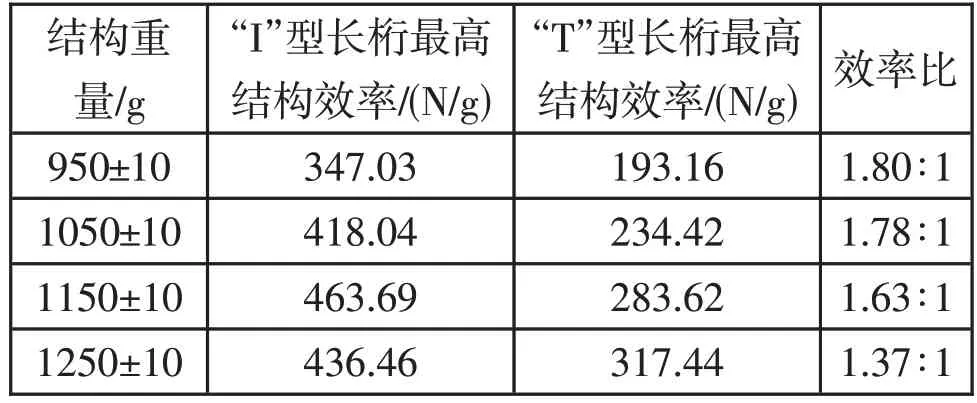
表5 翼梢区“I”型长桁与“T”型长桁加筋壁板结构效率表

图10 翼梢区“I”型长桁与“T”型长桁结构重量与承载效率散点图
4 结语
通过对复合材料尾翼盒翼根区、中间区和翼梢区不同构型加筋壁板结构承载效率的权衡分析,可以看出,总体上,“I”型长桁加筋壁板的结构效率高于“T”型长桁。因此,可以得出结论,在结构设计合理、承载效率相同的情况下,复合材料尾翼“I”型长桁加筋壁板可比“T”型长桁加筋壁板减重约15%以上。在实际工程应用中,使用“I”型长桁加筋壁板替代“T”型长桁加筋壁板,可以降低尾翼的结构重量。

