探讨圆弧导线电势的计算

王悦 刘宇 吴志豪 李南 王岚 何碧芸 方碧绿 梁靖琪 古俊 胡新春

（铜陵学院 安徽铜陵 244000）

静电场中，能够反映其本质的物理量是电场强度和电势，因而，电场强度的计算和电势的计算成了研究静电场特性和教师教学中的重点和难点［1-3］。静电场中，带电体的电势计算可以分成两大类，即电势叠加法和电势定义法。有限带电体电势的计算方法很多［4-6］。

1 电势计算举例

以一段圆弧均匀带电体为例，用不同方法进行求解。如图1所示，一个半径为R的均匀带电圆弧，圆心角为α，x轴平分α角，电荷线密度为λ，求弧心处的电势V。

图1 一段圆弧均匀带电导线模型

2 用电势叠加原理

2.1 叠加法

电势叠加原理是利用点电荷的电势求解任意带电体在空间产生的总电势。取无穷远为势能零点时，点电荷q在r处产生的电势为：

具体计算时，可以用式（1）求出电荷元产生的电势，再用叠加法求解总电势。

叠加法是由点电荷电势作为微元，通过积分，算出圆弧整体的电势。

对有限大的带电体取无穷远为势能零点时，点电荷q在距离点电荷为R处的电势可以写成下式：

如图2所示，电荷元dq在O点产生的电势为：

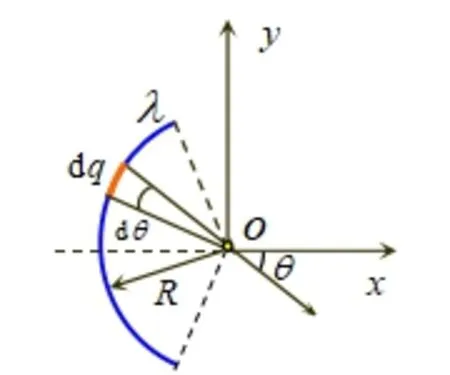
图2 取电荷元分析

则积分整个圆弧可以得到弧心处电势为：

2.2 挖补法

挖补法是由点电荷电势作为微元，通过积分，算出一个整圆电势，再求出圆弧的电势。

如图3所示，电荷元dq在O点产生的电势为：

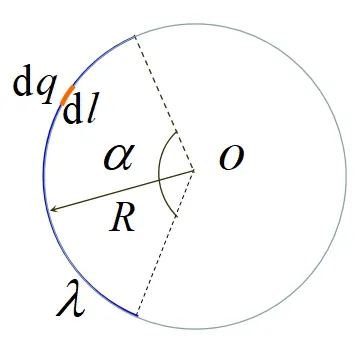
图3 挖补法求解图

那么，一个完整个圆环带电体O点产生的电势：

由角度为α时占整个圆的比例为α/2π，所以，圆弧在O点产生的电势为：

此结论与式（4）结果一致。

上述两种方法实质上都是采用电势的叠加原理，只是一种是先整体再局部，一种是从局部直接出发积分计算，其难易程度相当。

3 用场强积分方法

3.1 电势与电场强度的关系

由于静电场中某点的电势大小等于单位正电荷置于该点时的电势能，也等于单位正电荷，从该点经任意路径移到电势零点时，电场力所做的功出发，若试验电荷的电量为q0，根据电势的定义，a点处的电势Va等于电势能Wa与电量q0的比，即：

式（8）是电势的定义式，电势也叫电位。

由式（9）可见，电势可以通过电场强度积分路径求出。

电势是相对的，是标量，其大小与参考点的选取有关，原则上电势为零的参考点可以任意选取，但是，为了研究方便，一般对电荷分布为有限空间时，零参考点取在无穷远处。对于现在分析的一段圆弧，选取无穷远为势能零点，先算出空间从O点到无穷远的电场，再通过电场强度大小积分算出O点电势。

3.2 场强积分法

如图4所示，取x轴上任意一点P作为研究位置，dq在P点产生的电场为：

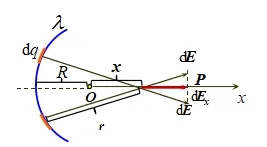
图4 场强积分法求解

由图中的几何关系可得：

所以有：

而总场为两倍x方向分量电场大小，从而得到总场的微分表达式为：

进而可以积分得到电场强度大小为：

当x≫R时，r=x+R，可得：

方向为x轴正方向。

4 结语

很容易看出式（4）、式（7）、式（16）的结论完全一致，可以用3 种不同计算方法求解同一个具体的物理问题。通过分析，可以发现，对于求解带电体在空间激发电场产生的电势，电势叠加原理和电势定义是通过电场强度的线积分求解，两种方法本质上都能计算。但是，同一问题往往难易程度相差很大，所以，计算不同带电体的电势要有针对性地选择合适方法。对于几何对称性好的，可以用电势叠加法，与场强积分方法相比在计算过程简化很多；对于没有对称性的，就只能用场强积分计算。这种一题多解的讲解方式能够使学生对类似问题了解得更清晰，能使学生更深刻地认识到电势的计算过程，有利于提高学生用已学知识解决实际问题的能力。