采用平方根高斯核积分滤波的目标跟踪算法

汪家宝,陈树新,吴昊,2,何仁珂,徐涵

(1.空军工程大学信息与导航学院,710077,西安;2.地理信息工程国家重点实验室,710054,西安;3.93184部队,100076,北京;4.95655部队,611530,成都)

非线性滤波和估计问题存在于信号处理、目标跟踪(例如水下跟踪、飞行器监视等)、组合导航等诸多领域[1-4]。目标跟踪是指利用相应传感器获得测量信号以完成对目标状态的连续迭代估计的过程,其中纯方位无源跟踪[5-6]能够被动地利用一系列角度信息完成目标的跟踪。由于其高非线性以及弱可观测性,对采用的非线性滤波估计算法要求较高。

目前,为了实现对非线性系统的状态估计,基于贝叶斯框架和高斯密度假设的高斯近似滤波得到了深入的研究,其核心是计算形如“非线性函数×高斯概率密度函数”的多维积分[7]。其中,扩展卡尔曼滤波[8]利用泰勒级数展开获得系统方程的近似表达,但在系统非线性程度较高时会引来较大的截断误差。基于“对概率分布进行近似要比对非线性函数近似容易”的认识,无迹卡尔曼滤波(UKF)[9-10]、高斯-厄米特积分滤波(GHQF)[11-12]、容积卡尔曼滤波(CKF)[13-14]等算法相继被提出,它们通过确定性采样来近似系统状态的后验概率密度,区别在于数值积分规则有所不同,分别采用无迹变换、高斯-厄米特积分规则以及容积准则。

考虑从数值逼近的角度提高估计精度,文献[15]推导了5阶球面-相径容积准则,建立了高阶CKF算法(HCKF),其比3阶CKF拥有更高的估计精度。Wang等采用5阶球面单纯形准则计算球面积分,提出了5阶球面单纯形-相径容积卡尔曼滤波[16],相比于HCKF可进一步提高估计精度。Bhaumik等将容积准则与高斯-拉盖尔积分规则结合,提出容积积分卡尔曼滤波(CQKF)[17]。CQKF是CKF的广义形式,当采用的切比雪夫-拉盖尔多项式阶数d≥2时,其精度高于CKF。GHQF采用高斯-厄米特积分(GHQ)规则进行数值逼近,可获得更高的估计精度,但GHQF运用张量积规则将单变量高斯积分扩展到多维积分,其计算复杂度随系统维数指数增长。事实上,随着各个领域对滤波精度的要求越来越高,如何进一步提高数值积分精度需要深入研究。

文献[18]推导了一种精确且数值稳定的高斯核积分权重近似值,该近似是建立在缩放的高斯-厄米特积分节点的基础上,但该数值积分方法并未系统地运用于高斯滤波过程。

因此,本文利用高斯核积分规则结合张量积方法推导了高斯核积分滤波算法(GKQF),该算法通过选定与高斯-厄米特积分节点成比例的积分点,采用高斯核积分规则计算出相应权重近似值,形成基于比例高斯-厄米积分点的高斯核积分规则,并与GHQF算法同样利用张量积方法实现多维积分,在运算量接近的情况下其能够获得比GHQF更好的滤波效果,并且可结合实际情况灵活调整参数。

同时,为了增强GKQF算法的数值稳定性,如同UKF、GHQF以及CKF的平方根版本[19-21]采用QR分解代替Cholesky分解,确保了协方差矩阵的半正定性从而改进数值的稳定性,本文推导了平方根高斯核积分滤波算法(SGKQF)。通过对典型二维非线性滤波系统与纯方位目标跟踪实例的仿真实验,验证了GKQF以及SGKQF算法相较于UKF、CKF、GHQF等传统算法具有更高的估计性能。

1 问题描述和高斯-厄米特积分规则

1.1 问题描述

考虑非线性离散时间状态空间模型

xk=f(xk-1)+wk-1

(1)

zk=h(xk)+rk

(2)

式中:xk∈nx和zk∈nz分别表示k时刻的状态向量和量测向量;f(·)和h(·)分别表示非线性系统的状态函数和测量函数;过程噪声wk和量测噪声rk是互不相关的均值为0的高斯白噪声,方差分别为Qk-1和Rk。

高斯滤波的前提是假设滤波分布近似服从高斯分布,状态xk的后验概率密度满足

(3)

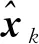
(4)

式中:Px=SST;Np为积分点数;ξl和ωl分别为随机变量y满足概率密度p(y)=N(y;0,Inx)时的积分点和相应权值,可根据GHQ规则、无迹变换或者容积准则来进行选取。

1.2 高斯-厄米特积分规则

对于具有高斯密度N(x;0,1)的标量x,采用数值近似获得非线性函数g(x)的期望,可通过高斯-厄米特积分规则计算ξl和ωl。传统的方法采用矩匹配法确定积分点和权重,但其计算较为复杂,一种简便方法是利用正交多项式和三对角矩阵之间的关系[11],假定J是一个具有0对角元素的对称三对角矩阵,其他元素计算式为

(5)

对于x是多维随机向量的情况,可通过张量积规则将单维获得的Np个积分点及相应权重扩展到多维积分[22]。

2 平方根高斯核积分滤波器

2.1 基于比例高斯-厄米特节点的高斯核积分规则

本文选取带比例因子的高斯-厄米特积分点,通过高斯核构造的线性方程组计算相应的核积分权重近似值,两者构成单变量高斯核积分规则的积分点与相应权重,再将获得的高斯核积分规则利用张量积方法从单变量扩展到多变量形式,使之适应多维积分的数值近似。

首先介绍运用高斯核技巧的高斯核积分规则。已知x,y∈,高斯核κ(x,y)定义为[23]

(6)

式中σ为高斯核带宽。

对于给出的互异积分点ξ=[ξ1,…,ξi,…,ξN]T,考虑函数f的数值积分形式[18]

(7)

如果积分权重ω=[ω1,…,ωi,…,ωN]T是通过线性关系计算出,则该数值积分规则称为高斯核积分规则。具体地,线性关系式为

κω=κI

(8)

单变量高斯核积分点ξ的一个特殊选择是单变量高斯-厄米特积分点的比例形式,比例因子的选择以及积分权重ω的计算此处不进行详细推导,直接给出引理。

(9)

(10)

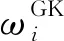
(11)

式(11)中的相关参数可定义为

(12)

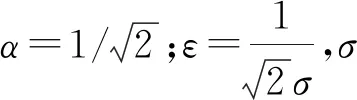
(13)

引理1可用于单变量数值积分近似,通过该方法获得的高斯核积分点以及相匹配的积分权重构成了本文所提算法的基础,可称为基于比例高斯-厄米特节点的高斯核积分规则,简称为高斯核积分规则。

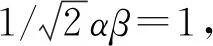
将单变量高斯核积分扩展为多变量积分的方法可利用张量积方法。张量积方法变换后的形式与多维高斯-厄米特积分相似,仅采用的积分点和权重不同,有

(14)

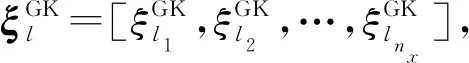
(15)

式中L=(Np)nx为多变量高斯核积分点数。

将张量积方法扩维后的高斯核积分点及相应权值置于高斯滤波框架之下获得的非线性滤波方法称为高斯核积分滤波GKQF算法。

2.2 高斯核积分滤波算法

与一般的高斯近似滤波相似,GKQF算法主要通过时间更新和量测更新两个步骤来实现。滤波过程如下。

(1)滤波初始化。

(16)

(17)

(18)

传播采样点

Xl,k|k-1=f(xl,k-1|k-1)

(19)

计算预测状态和预测协方差矩阵

(20)

Pk|k-1=

(21)

(22)

(23)

进行采样点的传播

(24)

计算预测量测及新息协方差矩阵

(25)

Pzz,k|k-1=

(26)

估计互协方差矩阵并计算滤波增益

Pxz,k|k-1=

(27)

(28)

k时刻的状态估计与估计协方差

(29)

(30)

2.3 平方根GKQF

GKQF算法存在协方差矩阵的平方根分解,为了提高滤波的数值稳定性,可采用QR分解来代替传统的Cholesky分解,这样便形成了平方根高斯核积分滤波算法。具体的实现方法如下。

(1)预测协方差平方根Sk|k-1被直接计算以进行积分点的传播,避免每一步运行时对Pk|k-1计算并进行因式分解。具体地,Sk|k-1计算式为

(31)

式中qr(·)表示QR分解,且有

(32)

(33)

利用式(31)替换式(21)(22)。

(2)新息协方差矩阵Pzz,k|k-1采用平方根形式

Szz,k|k-1=qr([Zk|k-1,SRk])

(34)

式中

(35)

(36)

进而,滤波增益调整为

(37)

(3)误差协方差平方根Sk-1|k-1被直接计算以避免对Pk-1|k-1计算并进行因式分解,即

Sk|k=qr([χk|k-1-WkZk|k-1,WkSRk])

(38)

式中

(39)

利用式(38)替换式(17)(30)。

3 仿真实验与分析

3.1 一类非线性滤波问题

为验证本文所提算法的有效性,考虑典型二维非线性系统

(40)

(41)

(42)

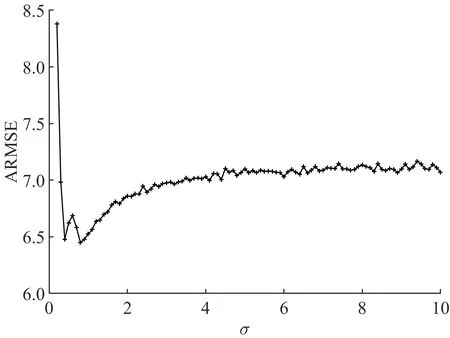
图1 不同σ下GKQF的平均均方根误差Fig.1 The eARMSE of GKQF with different σ

其次,将本文所提的GKQF、SGKQF算法与CKF、GHQF算法进行对比说明。各算法滤波精度仿真结果如图2所示。可以看出:当σ=0.4时,GKQF和SGKQF算法相较于UKF、CKF、GHQF具有更高的估计精度;当σ=10时,GKQF与GHQF均方根误差相接近,这与σ→∞时,GKQF等价于GHQF这一特性具有一致性。可以概括,当σ∈[0.4,10]时,GKQF可取得较GHQF更好的估计性能。

图2 各算法在状态1时的均方根误差比较Fig.2 The eRMSE comparison of different algorithms under state 1

综合可知,GKQF算法的精度随着高斯核带宽σ(从正无穷起始,当σ→∞,GKQF等价于GHQF)的减小而增加,但随着σ减小至一定数值后,误差急剧上升。因此,在仿真实验过程中可以先选取较大的高斯核带宽,通过向下逼近以获得更高的估计精度。

3.2 纯方位目标跟踪问题

本文主要考虑目标做匀速运动时的跟踪问题,所构建的目标相对运动系统方程可表示成

Xk=f(Xk-1,uk-1)+wk-1=FXk-1-uk-1+wk-1

(43)

式中:Xk∈nx;nx为状态向量维数;过程噪声wk-1是满足均值为0协方差为Qk-1的高斯白噪声;转移矩阵F、确定性输入uk-1以及Qk-1的表达式分别为

(44)

(45)

(46)

式中:Δt为采样间隔;q为过程噪声强度。

观测站纯方位跟踪的量测方程为

(47)

目标及观测站运动轨迹如图3所示,观测站的初始位置在(0,0),其在0～11 min和17～30 min作匀速运动,在12～16 min作机动运动。采样间隔Δt=1 min,仿真时长为30 min。过程噪声强度q=10-11km2/s3。

图3 目标及观测站运动轨迹Fig.3 The movement trajectory of target and observing station

(48)

图4和图5分别记录了各算法位置和速度均方根误差。其中,SGKQF算法分别选取高斯核带宽σ=2.5,3,3.5。可以看出,所提算法在σ=3附近可使纯方位目标跟踪的位置和速度误差达到最小,其滤波效果优于UKF、CKF、HCKF以及GHQF。仅考虑跟踪过程后20 min内的平均均方根误差,当高斯核带宽取为3时,相比于GHQF,SGKQF算法的位置和速度估计精度分别提高了8.7%和11.8%。从这两个例子可以发现,基于高斯核积分规则形成的GKQF和SGKQF算法具有更强的估计性能。

图4 各算法的位置均方根误差比较Fig.4 The eRMSEpos comparison of algorithms

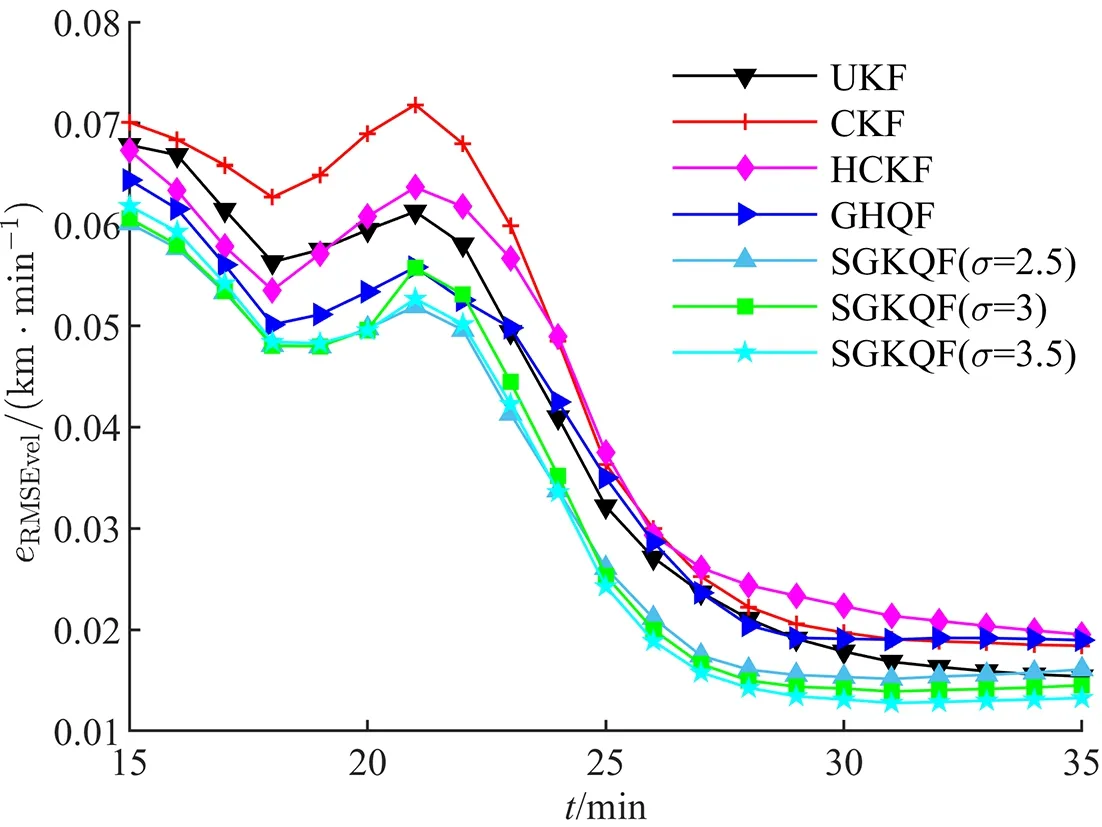
图5 各算法的速度均方根误差比较Fig.5 The eRMSEvel comparison of algorithms

表1给出了各算法的积分点数与相对运算时间,相对运算时间以CKF为基准,系统状态维数n=4。在运算复杂度方面,与CKF、UKF以及HCKF算法相比较,GHQF和SGKQF需要更多计算时间。SGKQF和GHQF的采样点数均为3n,其计算代价相近。SGKQF相较于GHQF在没有增加较大运算复杂度的前提下提高了目标跟踪精度,且能够通过调整高斯核带宽来适应不同的应用需求,灵活性更高。

表1 各算法的积分点数与相对运算时间Table 1 Quadrature points number and relative computation time of algorithms

4 结 论

本文以提高非线性系统滤波估计精度为目的,首先构造与高斯-厄米特积分节点成比例的积分点,采用高斯核构造的线性方程组计算出相应近似权重,建立了单变量高斯核积分规则。再利用张量积方法将其扩展为多维数值积分,并推导了高斯核积分非线性滤波的平方根形式,即SGKQF算法。通过仿真实验可得到以下结论。

(1)与GHQF算法相比,SGKQF算法能够在同等计算复杂度下获得更高的目标跟踪精度,且灵活性更强,体现了高斯核积分规则的优越性。同时,所提算法有望提高目标跟踪、信息融合等应用领域所涉及的非线性滤波的精度,能够获得更为精确的状态估计。

(2)在实际应用中,可以考虑采用高斯核带宽的经验取值,也可以提前进行实验测试获得更为准确的高斯核带宽以进一步提高滤波精度。此外,如何采用自适应方法来实时更新高斯核带宽,以及如何在高维非线性系统中降低算法计算复杂度也是未来的探索方向。