无底柱分段崩落法放矿方案数值模拟分析

许力峰

(中钢石家庄工程设计研究院有限公司， 河北 石家庄 05000)

无底柱分段崩落法是1950年代以来随着新型采矿工艺和设备的出现而逐步发展起来的一种高效率、高度机械化、结构简单、生产安全、成本较低廉的采矿方法，这种方法自1960年代以来，在国内外铁矿得到广泛应用，已成为分段崩落法的主要方案之一[1-2]。历年来，国内外学者和矿山对于影响该种采矿方法放矿效果的因素——采场结构参数（主要包括分段高度、进路间距和崩矿步距）进行了大量的试验和理论研究工作[3-8]，成果较为丰富，其中胡建华等[4]通过创建分段高度、进路间距、崩矿边孔角和截止贫化率4因素正交仿真模型，分析了在各采场结构参数因素相互影响下的矿石和废石的放出移动规律。而对于影响无底柱分段崩落法放矿效果的另一重要影响因素——放矿方案的研究相对较少，文献[9]提出，基于放矿时矿石与废石交接面的形状和变化趋势，放矿方案分成3种：平面放矿、立面放矿和斜面放矿，不同的放矿方案影响矿石回采率、贫化率等回采指标。其中，平面放矿表现为放矿时各位置矿岩分界线几乎同水平下移；立面放矿表现为各放矿口依次放矿，直至达到截止放矿条件。

本文采用PFC2D模拟单分段多进路平面放矿和立面放矿两种放矿方案的散体矿体放出规律，统计对比不同放矿方案对矿石回采率、贫化率的影响，并分析其原因，为优化无底柱分段崩落法放矿效果提供依据。

1 数值模型

为了强化研究的针对性，本次按照某一放矿工作面的垂直剖面建立了4条进路单分段的放矿模型，如图1所示，模型宽度为60 m，进路间距为15 m，分段高度为17 m，上覆废石厚度为25 m，进路宽为4 m，高为3 m，边孔角参数主要受凿岩设备和炮孔布置方式等的影响，本次选取边孔角为65°。由于建立的是二维模型，本次模拟暂不考虑崩矿步距因素。

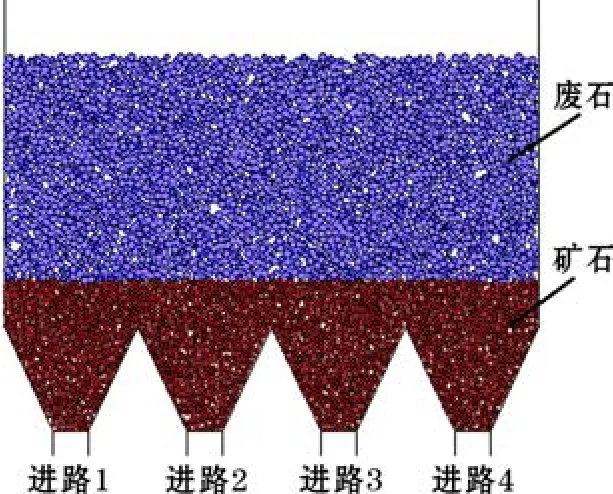
图1 PFC数值模型初始平衡状态

受爆破作用的影响，矿岩形成松散的堆体，但是各块体间仍然存在较小的黏聚力，为了保证模型一定的仿真度，本次设计矿石间的法向黏结力为100 N，切向黏结力为0 N，其接触力学微观参数见表1。

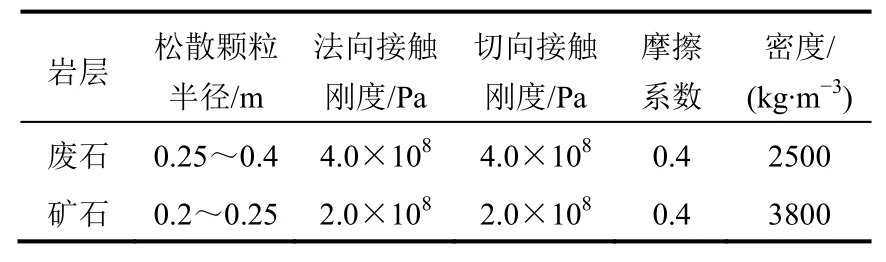
表1 矿岩模拟参数

模拟过程中，通过依次或全部删除约束颗粒的墙体，控制各进路依次或同时放矿，以此来分别实 现立面放矿和平面放矿效果。统计并对比各进路放矿至见废石后，在相同运行时步下的矿石和废石放出量，分析不同放矿方案的矿石回采率和贫化率（本次假设废石品位为0，即废石混入率等于贫化率），并以此进一步研究各放矿方案的优劣性。

2 模拟结果分析

2.1 矿石回采率和贫化率分析

2.1.1 立面放矿

立面放矿按照进路1至进路4依次放矿，图2为进路1放矿初次见废石时的模拟结果，根据统计初始模型生成的矿石量和放出的矿石量，计算得出进路1初次见废石时的矿石回采率为80.67%，形成了脊部残留矿石损失。最终放矿各进路形成了放矿漏斗，如图3所示，废石顶部边界线出现整体向右下倾斜现象。

图2 进路1放矿初次见废石模拟结果

图3 立面放矿模拟结果

统计计算并绘制了各进路放矿初次见废石后继续放矿的矿石回采率和贫化率对比曲线，如图4、图5所示。

图4、图5中0时刻为各进路放矿初次见废石时刻，由图4、图5可以看出，随着放矿的进行，各进路的矿石回采率和贫化率均不断增加，其中，进路1矿石回采率由83.41%增至85.10%，贫化率由10.26%增至16.00%；进路4矿石回采率由75.30%增至77.87%，贫化率由16.71%增至20.23%。整体而言，在相同的运行时步下，进路放矿越晚，矿石回采率越低，贫化率越高，其中进路4较进路1矿石回采率减少8.11个百分点，贫化率增加4.23个百分点。由图3也可以看出，各进路脊部残留矿石损失从进路1至进路4逐渐增大。

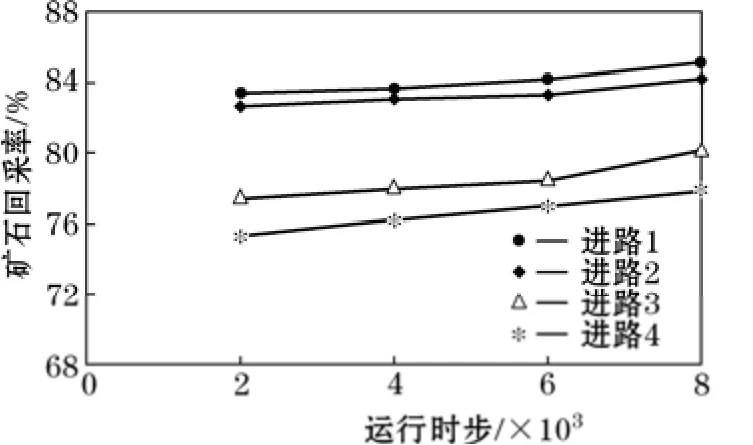
图4 立面放矿各进路矿石回采率对比

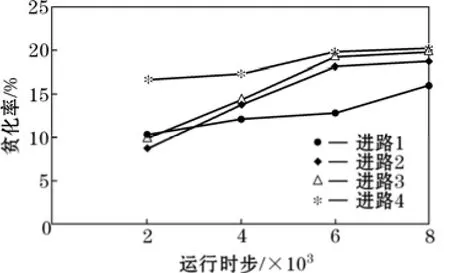
图5 立面放矿各进路贫化率对比

若设定放矿截止条件为贫化率16%，则进路2至进路4均需提前结束放矿，且提前结束时间依次增加，进一步影响矿石回采率。

另外，通过统计各进路初始放矿至初次见废石运行时步间隔，发现进路1至进路4各间隔分别为449 321，415 300，376 403和376 821时步，进路1至进路4放矿初次见废石间隔大体呈依次降低 规律。

2.1.2 平面放矿

平面放矿进路1至进路4同时放矿，图6为放矿初次见废石时的模拟结果，废石顶部边界线近似平缓，各进路几乎同时初次见废石，相差间隔在1000时步以内，平面放矿初次见废石时的矿石回采率为83.41%，各进路脊部残留矿石损失较平均。随着放矿的继续进行，各进路矿石回采率和贫化率相差不大，整体的矿石回采率和贫化率变化见表2，随着放矿的进行，各进路的矿石回采率和贫化率同样均不断增加。

图6 平面放矿模拟结果

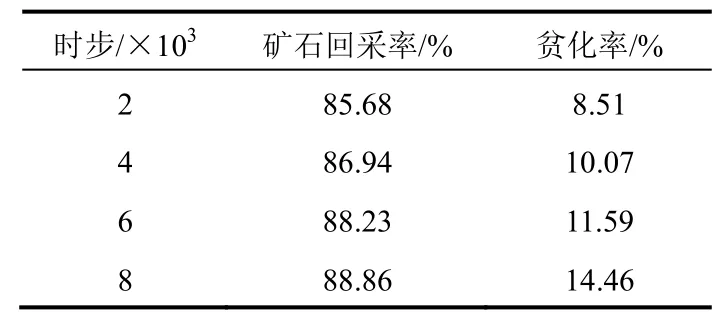
表2 平面放矿数据结果

2.1.3 对比分析

统计对比了两种放矿方案整体的矿石回采率和贫化率，如图7所示，初次见废石后在相同的放矿运行时步下，平面放矿方案在矿石回采率和贫化率方面均优于立面放矿，其中，平面放矿方案矿石回采率较立面放矿最大高出7.48个百分点，贫化率最大低5.94个百分点，优越性明显。

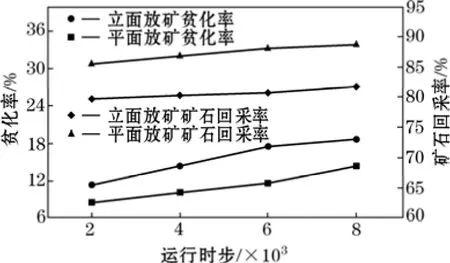
图7 两种方案放矿效果对比

2.2 矿石回采率和贫化率影响因素分析

2.2.1 椭球体放矿理论分析

根据椭球体放矿理论[2]，放矿时矿石是从放矿口上部的一个类似旋转椭球体内放出的，当该球体内全部为矿石时，放出的为纯矿石，在平面放矿过程中，各位置矿岩分界线几乎同水平下移且较稳定，放出椭球体内无废石混入，当相当于矿石层厚度的放出椭球体缩小并全部放出后，矿岩接触面形成降落废石漏斗，继续放矿，放出椭球体伸展至废石中，开始出现贫化，废石和矿石开始混合放出。

而在立面放矿过程中，由于进路1的提前放矿，扰乱了矿石和废石原有的分布状态，矿岩接触面变大，造成进路2放矿时，废石提前进入放出椭球体，理想的降落废石漏斗被打破，提前出现放出废石现象，见废石时间间隔缩短（即提前贫化），影响了矿石回采率。并且后边进路矿岩被扰乱更明显，最终造成立面放矿方案整体放矿效果劣于平面放矿。

同时，椭球体放矿理论认为，在理想状态下，放出椭球体表面颗粒同时到达放出口，只有处于稳定状态时放出椭球体才能被理想放出，前提是椭球体表面颗粒按各自迹线同时到达放矿口。而在自然状态下椭球体表面受外界因素的影响很难达到这种稳定状态，其多数处于紊乱状态，甚至出现局部椭球畸形，致使放矿损失在自然状态下不能完全消除[10]。图8为在不同放矿方案不同进路以矿石层厚度为长轴的放矿椭球体表面上，随机选取的两个散体矿石放出前后的速度-时间曲线，图8中速度最后急剧增大的转折点所对应的时刻为单元体从放矿口放出的时刻。

由图8可知，平面放矿进路1、立面放矿进路1、立面放矿进路2和立面放矿进路4的放矿椭球体表面两个散体矿石均未同时放出，放出的时间间隔分别为0.18万时步、0.2万时步、0.4万时步和0.7万时步，说明进路放矿越晚，放出椭球体表面的稳定程度越低。分析主要原因为：随着废石提前进入放矿椭球体，不同块度不同物理力学性质的矿岩散体相互作用加剧，并且在放出前离放矿口越近，矿岩速度变化范围越大，流动性相对增强，造成放出椭球体表面稳定性降低，进而影响放矿效果。

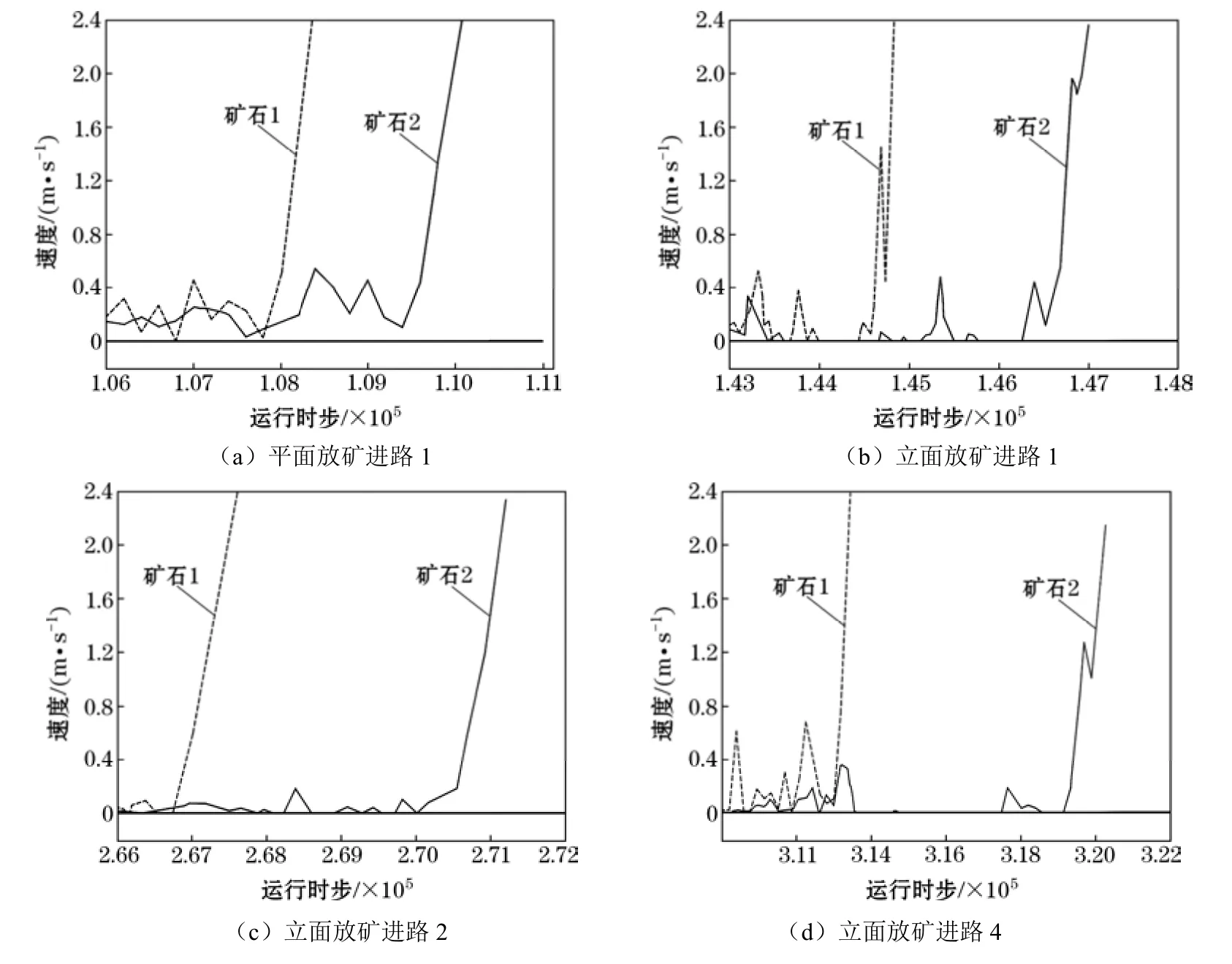
图8 不同放矿方案不同进路放矿椭球体表面散体矿石速度-时间

2.2.2 矿岩成拱

在实际生产中会出现放矿口堵塞现象，在模拟中表现为矿岩成拱，矿岩成拱是影响放矿效果的一个重要因素，矿岩成拱后直接影响放出椭球体的发育并影响放矿效率。由于本次模拟设定的放矿口尺寸相对矿石散体较大，平面放矿时各进路未出现成拱现象，而立面放矿时进路3和进路4各出现一次矿岩成拱。

分析主要原因为：立面放矿时，对于放矿较晚的进路3和进路4，粒径相对较大的废石提前进入放出体，使矿岩散体在放矿口处挤压成拱；另一方面，不同粒径的矿岩在放矿口放出时运动速度急剧增大，造成其在放出过程中相互挤压摩擦的几率增 大，易形成平衡结构拱。矿岩成拱进一步验证了平面放矿较立面放矿效果的优越性。

3 结论

（1）采用PFC2D离散单元体法模拟了无底柱分段崩落法立面放矿和平面放矿两种方案的矿石放出规律。结果显示立面放矿时，相同的运行时步下，进路放矿越晚，矿石回采率越低，贫化率越高。通过对比分析两种放矿方案整体的矿石回采率和贫化率发现，平面放矿方案均优于立面放矿，同等条件下能提高矿石回采率，降低贫化率。

（2）根据椭球体放矿理论分析了矿石回采率和贫化率的影响因素，立面放矿时，后放矿的进路，矿石和废石原有的分布状态被扰乱，矿岩接触面变大，废石提前进入放出椭球体，提前出现贫化，影响了矿石回采率。

（3）随机监测了不同放矿方案不同进路放矿椭球体表面散体矿石放出时的速度-时间变化曲线，得出进路放矿越晚，放出椭球体表面的稳定程度越低，进而影响放矿效果。通过矿岩成拱分析，进一步验证了平面放矿效果优于立面放矿。