基于模型参考自适应系统的电磁轴承支承转子不平衡量辨识及振动抑制

转子振动是限制旋转机械性能提升的关键因素之一,由于制造条件受限、转子材质不均匀以及加工装配误差等影响,由转子的质量不平衡造成的同频振动一直无法避免,特别是在高速旋转情况下尤为严重。因此,对旋转机械的振动控制尤为重要,而主动磁轴承(active magnetic bearings,AMB)通过电磁力将转子稳定地悬浮,具有电磁力主动可控的独特优势

,这使得对转子振动的主动控制成为可能。

目前,根据控制目标的不同,针对AMB转子系统的不平衡扰动抑制方法可分为自动平衡和不平衡补偿两类

。自动平衡通过消除电磁力中的同频成分使转子处于力自由状态从而趋近于绕惯性主轴旋转,达到降低传递到基座振动的目的。在磁轴承的自动平衡控制中,陷波器由于具有结构简单、实用性强的特点被广泛应用,且与前馈控制策略相结合,能最大限度地抑制不平衡力

。但是,引入陷波器会对闭环系统在低频段的稳定性造成影响,为此很多学者提出了极性切换陷波器

、相位补偿陷波器

等改进算法。自动平衡虽能够有效抑制不平衡力、降低系统的振动水平,但由于对转子位移的抑制效果较小,不适用于对转子回转精度要求较高的场合。

不平衡补偿是通过对转子位移信号中的转速同频分量进行辨识,据此生成补偿电流并添加到轴承线圈,产生能够抵消不平衡力的电磁力,从而强迫转子绕其几何轴旋转,使转子振动位移最小化。自适应迭代控制由于对模型的依赖度低,近些年来在不平衡补偿领域受到广泛关注,其中多边形迭代搜索是一种简单且有效的方法。为平衡算法收敛速度和辨识精度之间的矛盾,有学者提出了变步长搜索算法

、变角度搜索算法

等,取得了较好的补偿效果,但当不平衡扰动的频率和幅值增大时,搜索算法的收敛速度会变慢。针对振动抑制算法的信号提取过程占据大量计算资源的问题,Zheng等

提出了一种新型并行迭代学习控制机制,有效提高了算法的实时性并降低对系统模型的依赖。吴海同等

将同步旋转坐标系(SRF)变换与二阶广义积分(SOGI)相结合,取得了良好的控制效果,但是PI控制器的参数整定困难。自适应前馈控制(AFFC)作为一种典型的干扰补偿控制技术,在磁轴承的不平衡控制中也有应用,Yabui等

针对传统AFFC不能对频率实时变化的干扰进行补偿的问题,提出了一种具有频率估计算法的AFFC。干扰观测器的思想在不平衡补偿中也被广泛应用:Yu等

利用Lyapunov稳定性原理设计干扰观测器和控制器参数;Liu等

针对磁悬浮控制力矩陀螺稳定运行过程中电流刚度的不确定性和振动的不平衡,采用复合分层抗扰控制实现磁悬浮系统的稳定控制。

除上述控制算法之外,目前还有一些其他控制算法也被用于不平衡控制,如插入式谐振器

、变步长最小均方差(LMS)

、

综合控制

、

控制

等,但大多结构复杂,对控制器的性能要求很高。考虑到质量不平衡是转子的固有特性,在大多数情况下与运行条件无关,可先对不平衡量进行辨识,然后以此为基础直接生成补偿电流。针对转子的静态不平衡量辨识,目前也有相关研究。蒋科坚等

通过自适应搜索转子不平衡质径积的大小和方位产生控制信号,但搜索算法较为复杂,对硬件性能要求较高。Cui等

提出了一种简化的基于傅里叶系数识别的质量不平衡识别方法,但不平衡力的求解过程运算量较大。另外,上述辨识算法均改变了原有的闭环结构,导致算法的收敛性无法得到严格保证。

模型参考自适应系统(model reference adaptive systems,MRAS)由于具有结构简单、鲁棒性好、实用性强等优点

,在参数辨识领域得到了广泛应用,如辨识电机转速、定子电阻和转子磁链等参数,已被证明具有良好的辨识精度。本文将MRAS应用于电磁轴承-转子不平衡量的辨识。首先,在不影响原系统运行状态的情况下对不平衡量进行初步辨识,并据此生成补偿电流初始值。然后,针对模型误差和复杂工况带来的系统参数变化,提出了一种在线补偿算法。由于补偿过程只需对补偿电流进行微调,所以能够在保证补偿精度的基础上有效提高收敛速度。同时,利用Popov超稳定性理论设计自适应律和控制参数,并通过设计相位补偿角保证了控制算法在全转速范围内的稳定性。最后,通过仿真分析和实验研究验证了本文补偿算法的有效性。

1 电磁轴承支承转子的等效不平衡量

本文研究的电磁轴承-转子系统可简化为如图1所示的刚性转子径向四自由度模型。

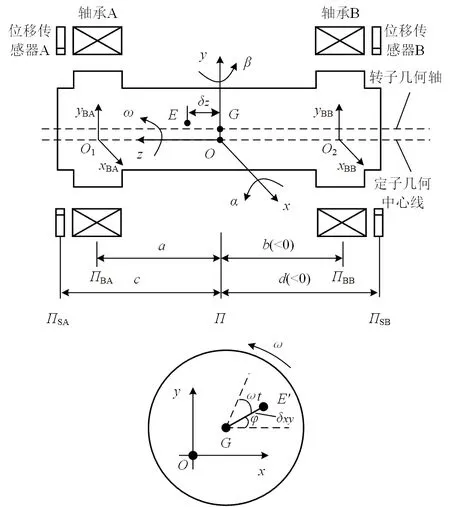
假设不平衡质量点

至质心平面的距离为

,将点

向平面

做投影,得到投影点为

′,

为

′点相对于质心

在转子径向的偏移量,

为初始状态下

′点与质心连线相对于

轴的偏移角。假设等效不平衡质量为

,忽略转子加速度的影响,不平衡力和力矩可表示为

(1)

根据转子动力学理论,电磁轴承-刚性转子的运动微分方程可写为

(2)

式中:

为转子质量;

、

分别为转子相对于

轴(

轴)和

轴的转动惯量;

A

、

B

、

A

、

B

分别为轴承A和轴承B在

和

方向的电磁力,表达式为

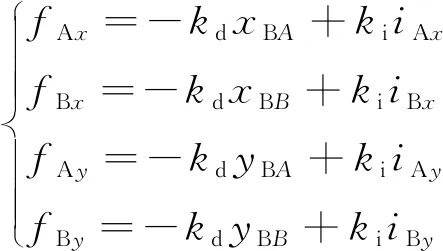
(3)

其中

和

分别为轴承的等效位移刚度系数和等效电流刚度系数。

根据式(2)的运动方程,可将不平衡力和力矩等效到两个轴承平面,然后在

和

方向上分别施加补偿电流产生相应的电磁力来抵消不平衡力,从而抑制转子的振动位移,此即不平衡补偿的基本思想。转子在轴承平面的等效不平衡力可表示为

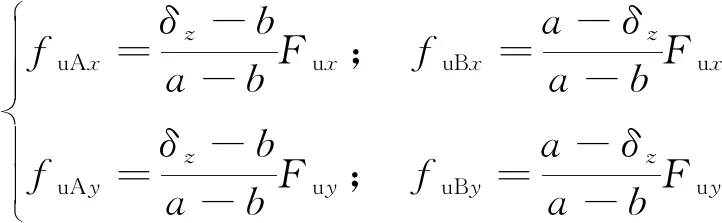
(4)

由于转子的不平衡质量是未知的,因此产生的等效不平衡力中的参数

、

、

和

也为未知量,要实现对不平衡振动位移的有效抑制,其关键在于对不平衡量的准确辨识。

从宏观层面上看，我国的企业在档案管理上缺乏重视，特别是高层管理人员，企业管理者对档案资源缺乏管理和利用的意识，这也会导致企业档案资源的管理具有落后性，难以跟上时代的脚步。在这样的恶性循环下，档案管理则受到了忽视。在档案管理的过程中，虽然将其地位放在“高处”，但是却缺少实际的操作管理，没有整合利用各项资源。而只有理念上的创新，才能真正意识到档案的社会价值、文化价值和实际产生的经济价值，故而可以推动大数据时代得到向前发展。[3]

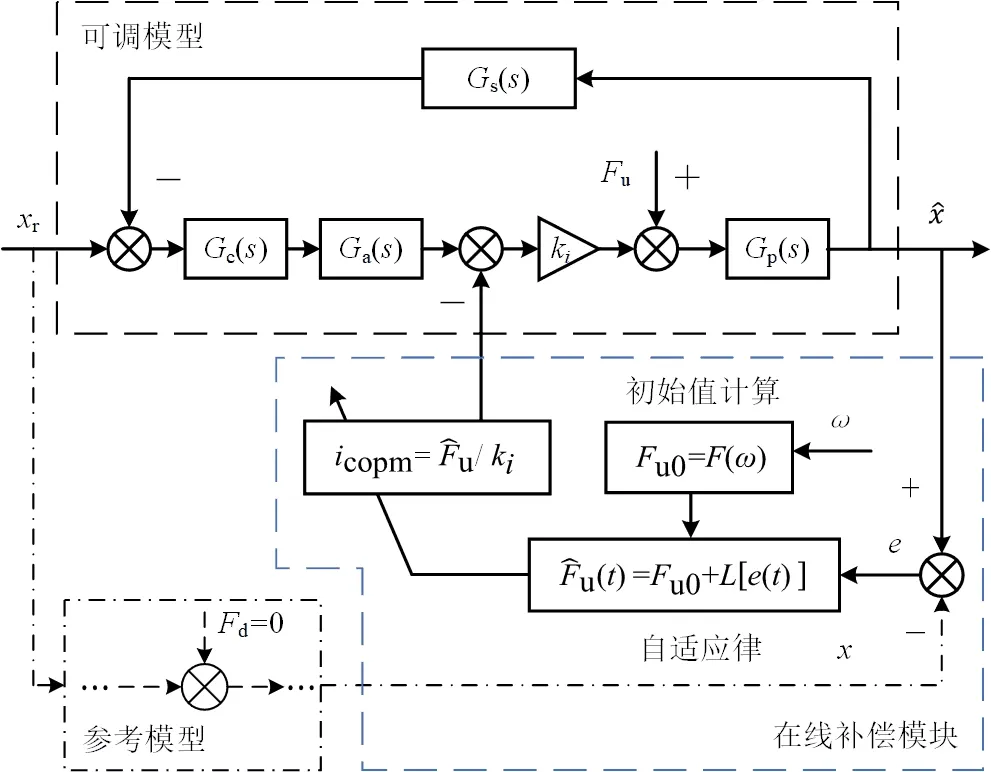
2 基于MRAS的转子不平衡量辨识及补偿

2.1 基于MRAS的不平衡量辨识模型

模型参考自适应系统包括一个参数明确的参考模型、一个含有不确定参数的可调模型和自适应律。模型参考自适应理论要求参考模型是稳定的、完全能观的和完全能控的

。图2是基于MRAS的不平衡量辨识算法框图,本文选取磁轴承单自由度控制系统本身作为参考模型,即参考位移信号作为模型输入,位移响应作为输出,其中

(

)为不完全微分PID控制器,增加惯性环节用于降低微分环节对干扰的敏感性以提高控制器性能,

(

)为位移传感器,

(

)为开关功放,

(

)为控制对象,各个模块的等效传递函数可表示为

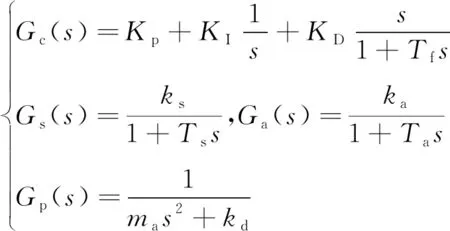
(5)

式中

为转子在轴承A平面的等效质量。

为描述转子的运动状态及便于位移检测和控制器设计,定义平衡转子质心所在径向平面为

,与质心平面

平行的轴承平面为

和

,传感器平面为

和

,各平面到质心平面的距离通过

方向的坐标值表示。以定子几何中心线与

平面的交点

为原点,建立固定参考坐标系

-

,其中

为转子的轴向,

和

符合右手定则。这样,转子的运动状态可通过质心

在

方向和

方向的平动以及转子绕

轴和

轴的转动描述,即

=[

-

]

。考虑转子的质量不平衡时,可将其等效为一个质心在

点的平衡转子附加一个不平衡质量点

,由于不平衡质量很小,一般认为质心位置变化很小,转子运动状态仍使用

点的广义坐标

描述。

为便于数字信号处理,仅考虑误差信号的转速同频分量,将其写成离散傅里叶级数形式

(6)

根据Popov超稳定性理论可以证明,在参数

和

的选取满足Popov不等式的情况下,闭环反馈系统是渐进稳定的

,推导可得自适应律参数的设计应满足

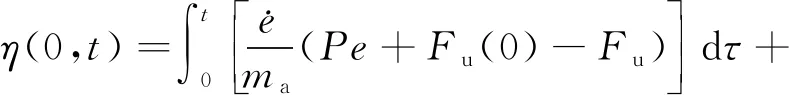
(7)

为分析相位补偿角对系统稳定性的影响,根据系统的等效传递函数,分别绘制相位补偿前后1～200 Hz下的系统特征方程的4个主导根轨迹,如图5所示。图中:横轴为复数坐标系的实轴;纵轴为复数坐标系的虚轴;

～

分别为系统的4个主导根。

2

1

1 振动信号处理及辨识算法实现

盐酸卡替洛尔口腔崩解片在Beagle犬体内的药动学研究…………………………………………………… 罗玲艳等（18）：2467

由于等效为干扰力的不平衡量是一个正弦时变信号,在实现方案中可将其转换为傅里叶系数进行辨识。以A端轴承

方向为例,由式(4)可知,在转速为

时的等效不平衡力可写为

乌托邦文学与“作为人类美好生活理念与情感的政治相关联”（刘锋杰等 2013：620），但是“当将政治关于美好生活的想象落实为制度，将制度分化为权力，将权力用于统治，并实现自身利益的最大化时，政治恐怕就与文学的想象发生冲突了”（同上：618）。“反乌托邦”文学正是着眼于展现政治现实与文学想象的冲突，对社会政治进行揭露、讽刺和批判。从这个意义上看，充满科幻色彩的“盎散克”的故事实则乃是一部社会寓言，是格雷对未来可能出现的威胁和风险的预测，以及对美好社会的渴望。

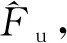
uA

=

[

cos(

+

)+

sin(

+

)]

(8)

式中:

为相位补偿角,用于保证辨识算法在全转速范围内的稳定性;

、

定义为不平衡系数,表达式为

本文基于实测水下地形和水文资料，建立了如东洋口港15万t级航道工程海域的三维潮流、泥沙数值模型，对工程海域的潮流分布、泥沙特性做了系统分析，得到以下结论：

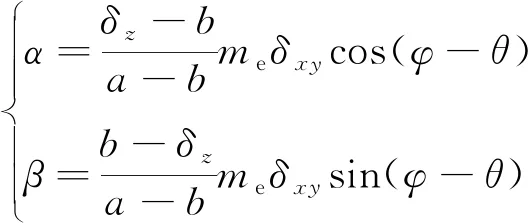
(9)

从上式可见,不平衡系数不仅取决于转子的不平衡质量,还取决于左右轴承的位置和相位补偿角。

由图8与图9可知，当微纳测头受到压电驱动力p=0 N时，测头的Z向刚度与Y向刚度分别为3.694 mN/μm与0.885 mN/μm。

蕉城区水利风景区内现存在的旅游解说系统只限于景区指示牌，甚至连最基本的游客服务中心和相关宣传材料都没有。随着社会科技和人工智能的发展，人们利用手机进行生活工作越来越频繁，人工智能也应用于各行各业，如何将人工智能与旅游解说系统结合，来发扬水利知识的传播是需要考虑的问题。

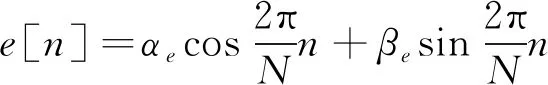
(10)

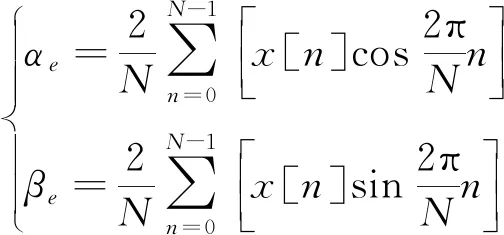
因此,两模型的误差信号

[

]可以通过式(10)求出其一阶分量的离散傅里叶系数

、

。以这两个傅里叶系数作为广义误差,此时的自适应律为

桥梁墩身的脚手架安装是墩身施工的关键问题。为了保证脚手架强度和稳定性，脚手架在焊接过程中一定要充分注意细节问题,做好材料焊接的每一个环节，严格按照图纸完成桥墩加固笼的焊接工作。除此以外，还要注意墩柱模板的安装,混凝土浇筑前的支架、模板等安装，在混凝土浇筑前一定要仔细检查桥墩固定架，防治浇筑模型出偏差而影响浇筑后的桥墩质量，从而影响桥体的施工质量。

(11)

2

1

2 辨识算法的稳定性

由于参考模型和可调模型的参数一致,可将两模型的误差信号表示为

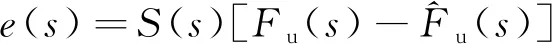
(12)

式中

(

)为原系统的灵敏度函数

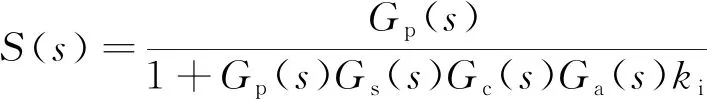
(13)

以实际不平衡干扰

为输入、误差信号

为输出,则系统的等效传递函数为

(14)

式中

为信号处理及自适应律的等效传递函数,公式为

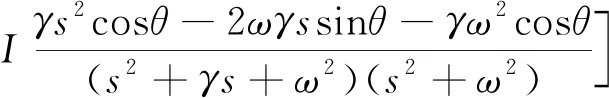
(15)

系统特征方程可写为

(

+

+

)(

+

)+

[

cos

+

(

cos

-

sin

)

+(

cos

-2

sin

)

-

sin

-

cos

]=0

(16)

当

=0即不引入辨识算法时,系统只有一个极点

=j

;当

≠0时,系统的极点将在

=j

的小范围邻域内变化。可将特征根

在

=0,

=j

处对

求导

4.统计学处理：数据用SPSS 17.0 统计软件进行统计学处理，结果用均数±标准差表示，样本比较采用t检验，P<0.05为差异有统计学意义。

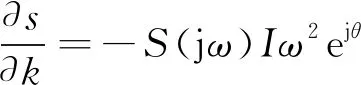
(17)

为保证闭环系统的稳定性,要求导数的实部小于0

Re[-

(j

)

e

j

]<0

(18)

因此,相位补偿角的取值范围为

-90°<[∠

(j

)]+

<90°

(19)

可见,为保证系统在全转速范围内的稳定性,相位补偿角需要根据转速进行适当调整,由式(9)可知,不平衡系数也会随之改变,即不同转速下的不平衡系数辨识结果是存在差异的,这与转子的固有不平衡质量无关,而是由相位补偿角的调整造成的。

2.2 转速自适应不平衡补偿

基于MRAS的辨识算法已证明是稳定的,为简化控制结构和提高算法实用性,补偿算法可直接采用与辨识算法相同的自适应律。图4是转速自适应补偿框图,参考MRAS参数辨识原理分析补偿算法的稳定性,将实际的控制系统视为可调模型,并假想一个外部干扰为0的参考模型,可调模型中的等效不平衡干扰力与补偿电磁力之差作为待辨识参数。

②石孝友《卜算子》(见也如何暮)：双调44字，上阕4句22字3仄韵，下阕4句22字3仄韵。句式：5575。5575。

学校立足艺术教育，必然要以特色课程作支撑。基于传承和发展本土嘉禾文化、岭南文化的背景，白云艺术中学大力建设“岭南艺术”特色课程，以音乐和美术系列为核心系列课程，兼设学科拓展系列和实践活动系列课程。特色课程让学生深入了解岭南艺术，促进学生对本土文化的认识和热爱，提升学生的艺术鉴赏力、分析力以及艺术素养，从而发展学生的艺术创作能力。

可见,采用基于MRAS辨识算法的自适应律能够保证补偿算法的收敛,消除了系统模型误差对辨识结果的影响,实现了对转子不平衡量造成的同频振动位移的完全补偿。

由于图4所示的控制回路模型适用于绝大多数电磁轴承控制系统,因此针对不同的应用场合,如压缩机、飞轮储能、机床电主轴等,只需对模型参数做相应修改,同时根据2.1小节中的思路对自适应律参数和相位补偿角进行合理设计,即可应用本文算法进行不平衡振动的抑制。

2011年区域内有80 394人，全部为农村人口，用水量134.3万m3，用水定额为 45.8L/（人·d）； 大牲畜 37 567头，用水定额为 60 L/（头·d）；小牲畜43035 头，用水定额为 25L/（头·d）。 实际灌溉面积27800亩（15亩=1 hm2，下同）其中菜田为7 700亩，用水量355.7万m3，其中菜田134.75万m3，用水定额水浇地为110m3/亩，菜田为175m3/亩。工业用水量为709万m3。2011年区域总用水量为1353.3万m3。

3 仿真结果及分析

(2)MRAS算法将不平衡控制过程分为两个阶段,在补偿阶段只需针对具体工况下的模型误差对补偿电流进行微调,相比一般的补偿算法,能够在保证控制精度的基础上极大地提高收敛速度,且在工况变化时也无需频繁更换控制参数。

3.1 相位补偿角验证

糖尿病疾病的治疗光靠药物治疗是远远不够的，还需要患者进行自我管理，对治疗工作进行配合。自我管理模式健康教育在很多社区医院都是很常见的，能够帮助医院患者进行自我管理，本文主要针对社区糖尿病自我管理模式健康教育效果的相关内容进行分析。

可以看出,在没有进行相位补偿前,系统极点在104 Hz左右开始进入正半平面,即高于该频率时辨识算法无法收敛,而在相位补偿后,系统极点均处于负半平面,即辨识算法在全频率范围内均可收敛。由此,相位补偿角选取的有效性得到了证明。

3.2 不平衡系数辨识与在线补偿

在仿真过程中设置幅值与转速平方成正比的正弦干扰

=0

000 035

cos(

+0.2π),以此模拟转子的不平衡力。仿真分析以A端轴承为例,分别取转子旋转频率为50、100、150 Hz,并设置一定的模型误差。为验证算法的抗干扰性能,施加一定的白噪声干扰,得到不同频率下的振动抑制效果和不平衡系数

、

的辨识轨迹,如图6所示,图中

为A端轴承

方向的振动位移。可以看出,在辨识阶段,设计的辨识算法能够准确预测误差方向,具有很快的收敛速度,且鲁棒性好,不同转速下的不平衡系数差异是由于相位补偿角的不同造成的。在补偿阶段,在线补偿算法采用辨识结果作为补偿的初始值,同时进一步对不平衡系数进行调整,能够基本实现对同频振动的完全抑制。因此,即使由于工况变化、非线性、高速耦合等因素导致模型误差,补偿算法依然具有良好的抑制效果。

为体现基于MRAS的辨识与补偿算法的优点,将其与一般迭代搜索算法的控制效果进行对比。以变步长迭代不平衡补偿算法为例,不同转速下的抑制效果及不平衡系数辨识轨迹如图7所示。

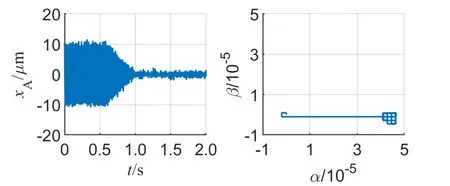
从图7可以看出,MRAS算法的优势主要体现在以下3个方面。

(1)MRAS辨识算法能够准确预测误差方向,从而更快速收敛到不平衡系数的位置,且不会出现局部最优的情况。

仿真和实验采用的电磁轴承-转子系统的主要参数如表1所示,其中,PID控制器参数为

=0.93,

=10,

=0.001,辨识及补偿算法的自适应律参数为

=0.000 3,

=0.01。

教学中可根据教材特点，多采用寓教于乐的练习，如在教学《角的度量》时，设计了量角的度数练习：游乐场有各种坡度不同的滑梯，小朋友去玩滑梯，选择哪种滑梯最合适？学生觉得这个练习特别有意思，为什么一样高的滑梯有的很平稳，而有的很危险呢？通过量角器测量得出角的大小与两条边长短无关与叉开的大小有关。这样既能提高学生学习的积极性，又能取得满意的练习效果。

(3)虽然变步长或变角度等改进可以平衡收敛速度和控制精度之间的矛盾,但是却无法有效适应转速的变化。随着转速的增加,转子的不平衡力幅值增加,此时收敛速度将会降低,而MRAS算法在不同转速下均表现出快速准确的抑制效果。

4 实验研究

本文所用的电磁轴承-转子系统实验平台如图8所示,主要包括电磁轴承-转子、驱动电机、LabVIEW上位机、DSP28377控制板、开关功率放大器、电涡流位移传感器、光电编码器等,其中主要装置的规格参数详见表1,控制系统采样频率为10 kHz。转子由两个径向电磁轴承支承,并由左侧的电机驱动,每个电磁轴承有8个磁极,气隙的最大磁密为1.2 T。

4.1 不平衡系数辨识及定速补偿

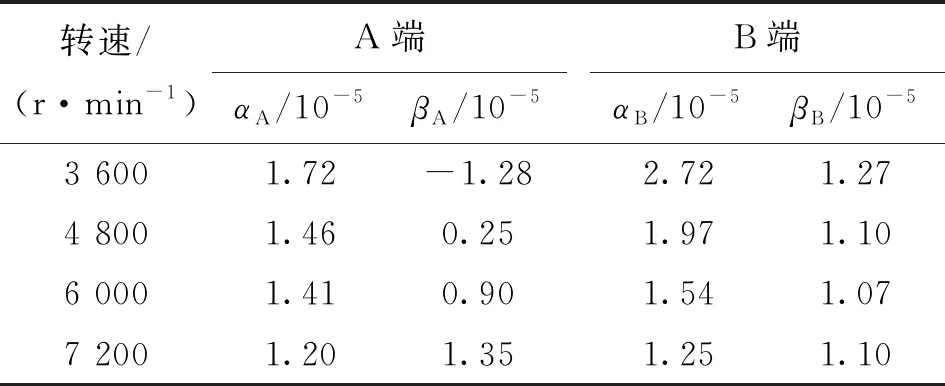
为验证算法在不同转速时的辨识和定速补偿效果,分别在固定转速为3 600、4 800、6 000、7 200 r/min时对转子的不平衡量进行辨识,得到不同转速下的不平衡系数,如表2所示。

根据转子的动平衡实验结果,可得表征不平衡量的相关参数近似值:

=34.5 g·mm,

=-5.05 mm,

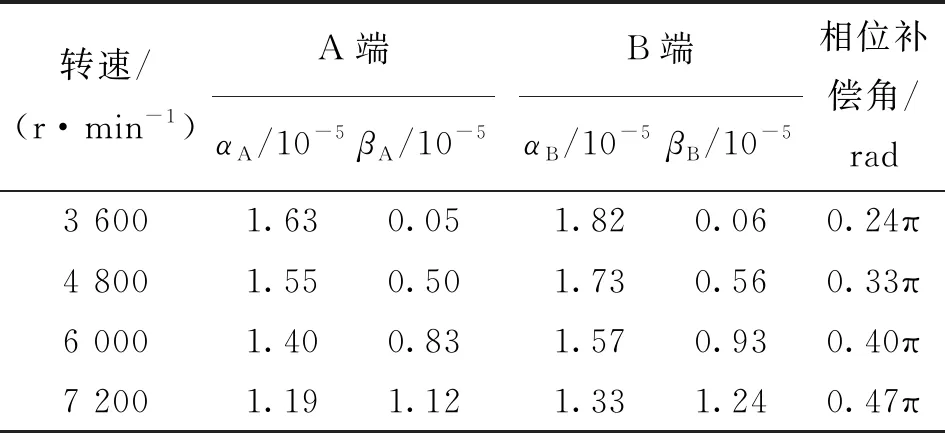
=0.23π rad。将这些参数及相位补偿角代入式(9),计算不同转速下的不平衡系数理论结果,如表3所示。将表3与表2相对比可以看出,算法在不同的转速下均能够收敛,且由于不同转速下的相位补偿角不同,同时功放的噪声干扰也会随之变化,导致不平衡系数的辨识结果存在一定的差异,尤其在低速不平衡干扰影响较小时的差异更为显著,但总体变化趋势与式(9)的理论结果是一致的。

以固定转速6 000 r/min为例,在

=1 s时开启在线补偿算法,得到补偿前后轴心运动轨迹、振动位移三维图及不平衡系数辨识轨迹,如图9所示。可以看出:未开启补偿算法时,转子A端轴承处的振动幅值为26 μm,B端轴承处的振动幅值为36 μm;开启在线补偿算法后,两端轴承的振幅在0.2 s内迅速衰减到12和10 μm并保持稳定,具有很高的收敛速度,保证了控制的实时性。此外,由于辨识阶段存在模型误差,可以发现补偿算法进一步对不平衡系数进行了微调。

对补偿前后转子在4个径向的振动位移进行频谱分析,结果表明,补偿前后4个径向位移的同频分量分别减小了99%、91%、99%、92%,说明补偿算法对于同频振动具有很好的抑制效果。

4.2 转速自适应补偿

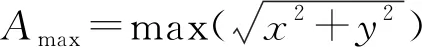
5 结 论

针对电磁轴承-转子系统中转子质量不平衡引起的扰动,本文提出一种基于MRAS的不平衡量辨识算法,对转子的固有不平衡质径积进行自适应辨识,并针对不同的转速和实际工况,根据辨识结果生成补偿电流的初始值,采用在线补偿算法对补偿电流进行微调。通过仿真和实验研究,得出以下结论:

(1)通过利用Popov超稳定性理论设计自适应律的控制参数并增加相位补偿角保证了辨识算法在全转速范围内都具有很好的稳定性,能够在不同转速下对转子的不平衡质径积进行初步辨识,并得到补偿电流的初始值;

(2)补偿算法无须频繁更换控制参数,只须针对具体运行工况带来的模型参数变化在补偿电流初始值的基础上进行微调,即可快速抑制同频振动,在保证补偿精度的前提下,提高了补偿算法的收敛速度,降低了算法计算负荷,增强了控制系统的实时性;

(3)设计的算法具有良好的自适应性和很强的鲁棒性,能够有效抑制转子在不同转速下的同频振动位移,且能够快速响应变转速导致的不平衡力变化,在定速和变速工况下均表现出很好的同频振动抑制效果;

(4)本文采用的控制回路模型具有普适性,针对一般的电磁轴承应用场景,只须对电磁轴承转子模型参数进行修改并对相关控制参数进行调整,即可利用本文算法实现对不平衡振动位移的有效抑制。

:

[1] 张维煜,朱熀秋,袁野.磁悬浮轴承应用发展及关键技术综述 [J].电工技术学报,2015,30(12):12-20.

ZHANG Weiyu,ZHU Huangqiu,YUAN Ye.Study on key technologies and applications of magnetic bearings [J].Transactions of China Electrotechnical Society,2015,30(12):12-20.

[2] 施佳余,吴国庆,茅靖峰,等.磁悬浮轴承系统控制方法研究 [J].机械设计与制造,2015(12):265-268.

SHI Jiayu,WU Guoqing,MAO Jingfeng,et al.Research of magnetic bearing system control method [J].Machinery Design &Manufacture,2015(12):265-268.

[3] LIU Gang,LI Jinlei,ZHENG Shiqiang,et al.Suppression of synchronous current using double input improved adaptive notch filter algorithm [J].IEEE Transactions on Industrial Electronics,2020,67(10):8599-8607.

[4] ZHENG Shiqiang,FENG Rui.Feedforward compensation control of rotor imbalance for high-speed magnetically suspended centrifugal compressors using a novel adaptive notch filter [J].Journal of Sound and Vibration,2016,366:1-14.

[5] 巩磊,杨智,祝长生,等.基于极性切换自适应陷波器的磁悬浮高速电机刚性转子自动平衡 [J].电工技术学报,2020,35(7):1410-1421.

GONG Lei,YANG Zhi,ZHU Changsheng,et al.Automatic balancing for rigid rotor of magnetically levitated high-speed motors based on adaptive notch filter with polarity switching [J].Transactions of China Electrotechnical Society,2020,35(7):1410-1421.

[6] PENG Cong,HE Jiaxi,ZHU Mengting,et al.Optimal synchronous vibration control for magnetically suspended centrifugal compressor [J].Mechanical Systems and Signal Processing,2019,132:776-789.

[7] LIU Yang,MING Shuaishuai,ZHAO Siyao,et al.Research on automatic balance control of active magnetic bearing-rigid rotor system [J].Shock and Vibration,2019,2019:3094215.

[8] 毛川,祝长生.主动电磁轴承刚性转子系统实时变步长迭代不平衡补偿 [J].中国电机工程学报,2018,38(13):3960-3968.

MAO Chuan,ZHU Changsheng.A real-time variable step size iterative unbalance compensation for active magnetic bearing-rigid rotor systems [J].Proceedings of the CSEE,2018,38(13):3960-3968.

[9] 蒋科坚,王骏,祝长生.适合变速转子的不平衡质径积搜索电磁轴承振动抑制 [J].机械工程学报,2018,54(21):72-80.

JIANG Kejian,WANG Jun,ZHU Changsheng.Vibration suppression by seeking unbalance mass-radius product in active magnetic bearing-rotor system with varying speed condition [J].Journal of Mechanical Engineering,2018,54(21):72-80.

[10] 巩磊,祝长生.基于变角度补偿算法的磁悬浮高速电机刚性转子系统的不平衡振动抑制 [J/OL].中国电机工程学报[2021-08-01].https:∥kns.cnki.net/kcms/detail/detail.aspx?doi=10.13334/j.0258-8013.pcsee.200096.

GONG Lei,ZHU Changsheng.Unbalance vibration suppression of an active magnetic bearings-rigid rotor system for high-speed motors based on variable angle compensation algorithm [J/OL].Proceedings of the CSEE[2021-08-01].https:∥kns.cnki.net/kcms/detail/detail.aspx?doi=10.13334/j.0258-8013.pcsee.200096.

[11] ZHENG Yangbo,MO Ni,ZHOU Yan,et al.Unbalance compensation and automatic balance of active magnetic bearing rotor system by using iterative learning control [J].IEEE Access,2019,7:122613-122625.

[12] 吴海同,周瑾,纪历.基于单相坐标变换的磁悬浮转子不平衡补偿 [J].浙江大学学报(工学版),2020,54(5):963-971.

WU Haitong,ZHOU Jin,JI Li.Unbalance compensation of magnetically suspended rotor based on single phase coordinate transformation [J].Journal of Zhejiang University (Engineering Science),2020,54(5):963-971.

[13] YABUI S,INOUE T.Development of adaptive feed-forward cancellation with frequency estimation algorithm for compensation of periodic disturbance at arbitrary frequency [J].Journal of Dynamic Systems,Measurement,and Control,2019,141(12):121014.

[14] YU Yuanjin,YANG Zhaohua,HAN Chao,et al.Disturbance-observer based control for magnetically suspended wheel with synchronous noise [J].Control Engineering Practice,2018,72:83-89.

[15] LIU Yifan,LIU Gang,XIE Jinjin,et al.Rotor unbalance vibration suppression for MSCMG using composite anti-disturbance control method [C]∥Proceedings of the 2019 Chinese Control Conference (CCC).Piscataway,NJ,USA:IEEE,2019:3272-3277.

[16] KANG C,TSAO T C.Control of magnetic bearings for rotor unbalance with plug-in time-varying resonators [J].Journal of Dynamic Systems,Measurement,and Control,2016,138(1):011001.

[17] 周天豪,陈磊,祝长生,等.基于自适应变步长最小均方算法的磁悬浮高速电机不平衡补偿 [J].电工技术学报,2020,35(9):1900-1911.

ZHOU Tianhao,CHEN Lei,ZHU Changsheng,et al.Unbalance compensation for magnetically levitated high-speed motors based on adaptive variable step size least mean square algorithm [J].Transactions of China Electrotechnical Society,2020,35(9):1900-1911.

[18] PESCH A H,SAWICKI J T.Active magnetic bearing online levitation recovery through μ-synthesis robust control [J].Actuators,2017,6(1):2.

[19] GOTO M,MIZUNO T,TAKAMI I,et al.Robust

control for active magnetic bearing system with imbalance of the rotor [C]∥Proceedings of the 2016 IEEE 14th International Workshop on Advanced Motion Control (AMC).Piscataway,NJ,USA:IEEE,2016:297-303.

[20] CUI Peiling,HE Jingxian,FANG Jiancheng.Static mass imbalance identification and vibration control for rotor of magnetically suspended control moment gyro with active-passive magnetic bearings [J].Journal of Vibration and Control,2016,22(10):2313-2324.

[21] 陈有鹏,卜文绍,张晓峰,等.无轴承异步电机的无功功率MRAS转速辨识研究 [J].控制工程,2020,27(7):1118-1124.

CHEN Youpeng,BU Wenshao,ZHANG Xiaofeng,et al.Research on speed identification of reactive power MRAS for bearingless induction motor [J].Control Engineering of China,2020,27(7):1118-1124.

[22] 董宁.自适应控制 [M].北京:北京理工大学出版社,2009.

[23] ISO.Mechanical vibration-vibration of rotating machinery equipped with active magnetic bearings:part 2 evaluation of vibration:ISO14839-2[S].London,UK:ISO,2004:35.