无人水下航行器全局路径规划及有限时间跟踪控制

滕建平 梁霄 陶浩 龚俊斌 曲星儒

摘要：为解决复杂航行环境下无人水下航行器（unmanned underwater vehicle， UUV）路径规划及跟踪控制问题，提出一种考虑避障的全局路径规划策略及实现有限时间精确路径跟踪的控制方法。基于改进人工势场法得到一条可跟踪且避免碰撞的全局路径，为UUV实现精确路径跟踪奠定基础。

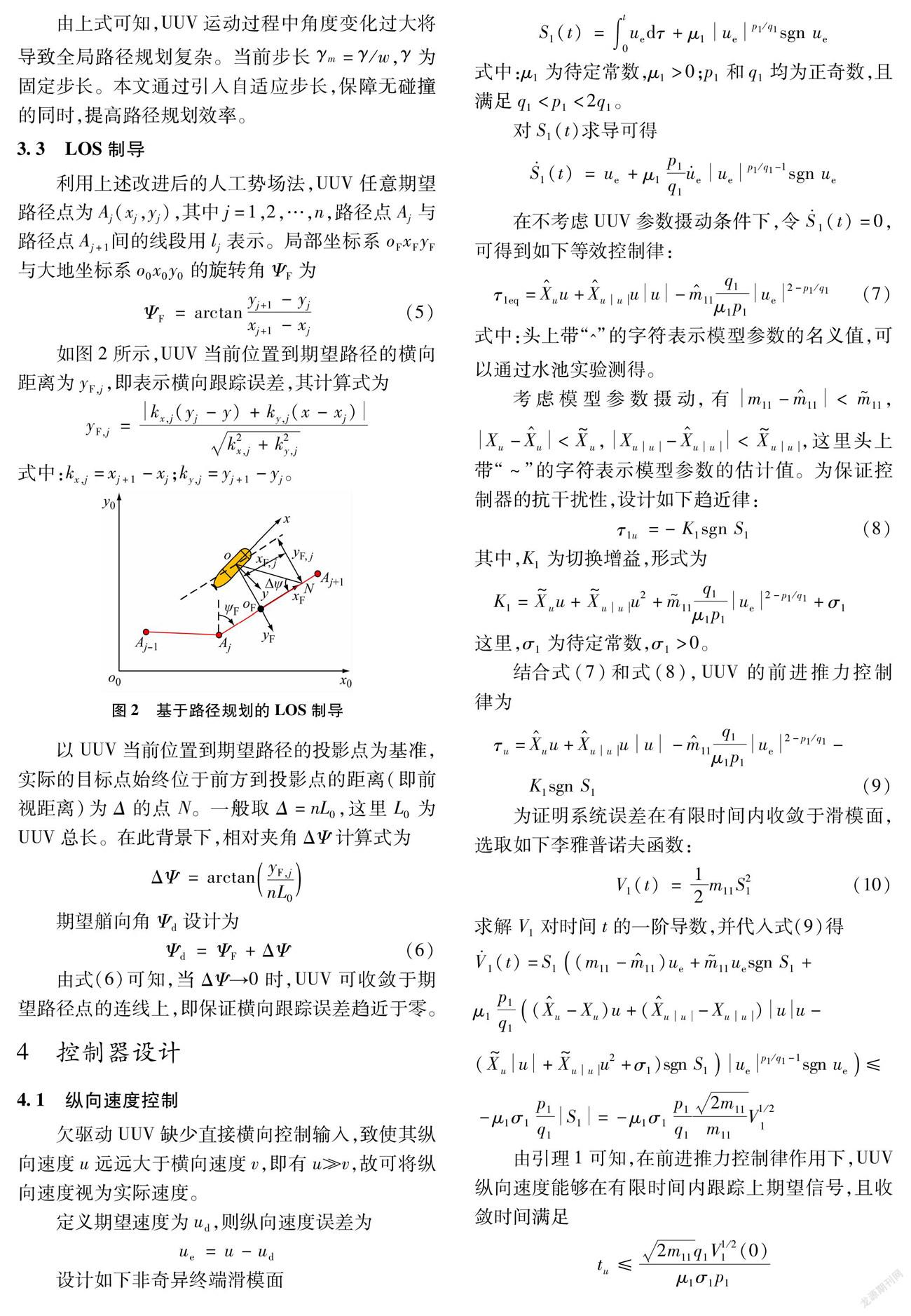
引入Serret-Frenet坐标系，并设计用于路径规划的视线（line-of-sight，LOS）制导方法。基于非奇异终端滑模控制设计UUV控制律，确保系统误差可以在有限时间内趋近于零。基于李雅普诺夫稳定性理论证明所设计控制系统的稳定性，仿真实验验证了所设计的UUV路径规划及跟踪控制方法的有效性。路径规划模块与路径跟踪模块有效结合更加符合实际UUV工作环境的需要，具有重要的实际意义。

关键词：

无人水下航行器; 全局路径规划; 跟踪控制; 人工势场法; 非奇异终端滑模

中图分类号：  U674.941; U664.82

文献标志码：  A

Global path planning and finite-time tracking control of

unmanned underwater vehicles

TENG Jianping1， LIANG Xiao1， TAO Hao2， GONG Junbin2， QU Xingru1

（1.Naval Architecture and Ocean Engineering College， Dalian Maritime University， Dalian 116026，

Liaoning， China; 2.China Ship Research and Design Center， Wuhan 430064， China）

Abstract：

To solve the problem of path planning and tracking control of unmanned underwater vehicles （UUVs） in complex navigation environment， this paper presents a global path planning strategy considering obstacle avoidance and a control method to realize finite-time accurate path tracking. Based on the improved artificial potential field method， a global path that can be tracked and avoid collision is obtained， which lays the foundation for the accurate path tracking of UUVs. The Serret-Frenet coordinate system is introduced and the line-of-sight （LOS） guidance law is designed for the path planning. The UUV control law is designed based on the non-singular terminal sliding mode control， which can ensure that the system error converges to zero within a finite time. The stability of the designed control system is proved based on the Lyapunov stability theory， and the simulation results show the effectiveness of the designed path planning and tracking control method. The effective combination of the path planning module and the path tracking module is more in line with the needs of the actual UUV working environment， which has important practical significance.

Key words：

unmanned underwater vehicle; global path planning; tracking control; artificial potential field method; non-singular terminal sliding mode

0 引 言

无人水下航行器（unmanned underwater vehicle， UUV）在水文调查、海洋勘探、救助打捞作业中有非常重要的应用，近年来UUV路径规划及跟踪成为研究热点。然而，由于UUV自身的水动力特性复杂，各个自由度之间耦合性强，同时还受到不确定的水下环境（如海流、波浪等）的干扰，UUV系统具有较强的非线性、耦合性以及模型不确定性[1-2]。

目前，模糊控制法[3-4]、遗传算法[5]、人工势场法[6-9]等智能优化算法被广泛应用到路径规划中。林政等[3]考虑障碍物所有分布情况设计模糊推理规则表，使航行器能够根据环境变化调整航速，增强了航行器对未知、复杂环境的适应能力。考虑海洋环境的特殊性对航行器路径规划的影响，YAO等[5]对遗传算法中的变异因子进行改进，规划出最优的路径。YANG等[9]针对人工势场法目标不可达问题，通过引入相對速度和相对距离来改进势场函数。gzslib202204031033

跟踪控制问题作为构建UUV系统的基础，近年来已成为各国学者研究的热点，并取得了丰富的研究成果[10]。目前，常见的跟踪控制方法有反步控制[11-12]、神经网络控制[13]、滑模变结构控制等[14-15]。LAPIERRE等[11]针对水下航行器的水平面路径跟踪问题，基于虚拟向导建立路径跟踪误差方程，基于反步法设计艏向控制器。边信黔等[14]采用滑模变结构控制方法进行水下航行器路径跟踪控制器设计，并考虑了航行器模型参数不确定性和海流干扰的影响，减小了输出反馈控制的稳态误差和超调问题。霍宇彤等[15]引入Serret-Frenet局部坐标系和视线（line-of-sight， LOS）制导律，将路径跟踪的位置误差镇定转换为视线角误差镇定，并通过引入径向基函数（radial basis function， RBF）神经网络和积分滑模面，设计动力学路径跟踪控制器。高剑等[16]利用非线性系统级联的方法，将三维直线跟踪系统误差模型分解为一个独立的垂直面运动系统和一个受垂直面运动扰动的水平面运动系统，级联系统不需要设计整个系统的李雅普诺夫函数，控制律设计更加简洁。王宏健等[17]针对欠驱动水下航行器的三维直线路径跟踪问题，引入虚拟向导建立了三维航迹误差模型，合理选择控制器参数，消除了非线性项，简化了控制器设计步骤。

鉴于此，本文在传统人工势场法的基础上，引入目标点距离影响因子以避免出现局部极小值和目标不可达问题，考虑路径规划的复杂度，设计自适应步长调节，实现复杂海洋环境下的路径规划;其次通过引入Serret-Frenet坐标系，设计基于路径规划的LOS制导方法，以免UUV距离期望路径过远而无解。考虑模型参数摄动问题，基于非奇异终端滑模设计全局有限时间控制律，确保系统误差在有限时间内收敛到零。基于李雅普诺夫稳定性理论证明所设计控制系统的稳定性，仿真实验表明所设计的UUV路径规划及跟踪控制方法的有效性。

5 仿真实验

为验证路径规划及控制策略的有效性，选取文献[20]的UUV进行仿真实验。

全局路径规划中：初始位置为A0（31 m，34 m），目标位置为Atar（900 m，930 m）;

障碍物位置分别为O1（400 m，400 m），O2（500 m，590 m）和

O3（800 m，800 m）;路径规划参数ξatt=8，ξrep=3，D=35 m，γ=0.8 m。

UUV期望速度为ud=1 m/s;初始状态为x（0）=0，y（0）=5 m，Ψ（0）=120°，u（0）=0，v（0）=

0，r（0）=0;控制器参数设置为μ1=0.5，p1=7，q1=5，σ1=3.5，μ2=1，μ3=2，p2=7，q2=5，σ2=10。模型参数存在10%的摄动，仿真结果见图3～10。

从图3可以看出，基于改进的势场法得到了一条全局避障路径。图4给出UUV跟踪上述规划路径的行为曲线。由图4可见，本文设计的有限时间控制律可以实现快速、精确的路径跟踪控制。由图5和6可以看出误差出现在起点以及路径切换的位置。图7为纵向跟踪和横向跟踪误差曲线，其中误差不为零且波动的情况主要是由规划路径的切换造成的。

除位置跟踪外，本文在前进推力和偏航力矩控制律下，实现了速度和艏向角跟踪。由图8和9可知，所设计的控制律输出状态平缓，系统收敛于期望值。由圖10可以看出，控制输入曲线较为平滑，抖振较小，均在执行机构作业范围内，其间出现的较小波动主要是由路径切换造成的，满足实际要求。

6 结 论

本文在无人水下航行器（UUV）路径规划的基础上，研究UUV路径跟踪控制问题。设计一种自适应人工势场法，减少多余的路径点，为UUV实现路径跟踪奠定基础。为使UUV精确跟踪基于人工势场法规划出的路径，引入Serret-Frenet坐标系，并设计基于路径规划的视线（LOS）制导方法。基于非奇异终端滑模控制设计UUV控制律，确保系统误差可以在有限时间内趋近于零。最后基于李雅普诺夫稳定性理论证明所设计控制系统的稳定性，仿真实验验证了所设计的UUV路径规划及跟踪控制方法的有效性。本文侧重于路径规划与路径跟踪控制的衔接，路径规划及跟踪控制的方法相对较为基础，还需进一步改进。如何克服艏向角出现的跳变问题以及优化研究方法将是下一步的工作重点。

参考文献：

[1]李硕， 刘健， 徐会希， 等. 我国深海自主水下机器人的研究现状[J]. 中国科学： 信息科学， 2018， 48（9）： 1152-1164. DOI： 10.1360/N112017-00264.

[2]钟宏伟， 李国良， 宋林桦， 等. 国外大型无人水下航行器发展综述[J]. 水下无人系统学报， 2018， 26（4）： 273-282. DOI： 10.11993/j.issn.2.96-3920.2018.04.001.

[3]林政， 吕霞付. 基于改进模糊算法的水面无人艇自主避障[J]. 计算机应用， 2019， 39（9）： 2523-2528. DOI： 10.11772/j.issn.1001-9081.2019020317.

[4]LIANG X， QU X R， WANG N， et al. Three-dimensional trajectory tracking of an underactuated AUV based on fuzzy dynamic surface control[J]. IET Intelligent Transport Systems， 2020， 14（5）： 364-370. DOI： 10.1049/iet-its.2019.0347.

[5]YAO P， ZHAO S Q. Three-dimensional path planning for AUV based on interfered fluid dynamical system under ocean[J]. IEEE Access， 2018， 6： 42904-42916. DOI： 10.1109/ACCESS.2018.2861468.gzslib202204031033

[6]LIANG X， QU X R， HOU Y H， et al. Distributed coordinated tracking control of multiple unmanned surface vehicles under complex marine environments[J]. Ocean Engineering， 2020， 205： 1-9. DOI： 10.1016/j.oceaneng.2020.107328.

[7]李沛伦， 杨启. 基于改进人工势场法的水下滑翔机路径规划[J]. 舰船科学技术， 2019， 41（7）： 89-93. DOI： 10.3404/j.siin.1672-7649.2019.04.17.

[8]姚鹏， 解则晓. 基于修正导航向量场的AUV自主避障方法[J]. 自动化学报， 2020， 46（8）： 1670-1680. DOI： 10.16383/j.aas.c180 219.

[9]YANG X， YANG W， ZHANG H J， et al. A new method for robot path planning based artificial potential field[C]//2016 IEEE 11th Conference on Industrial Electronics and Applications. IEEE， 2016： 1294-1299. DOI： 10.1109/ICIEA.2016.7603784.

[10]QU X R， LIANG X， HOU Y H， et al. Path-following control of unmanned surface vehicles with unknown dynamics and unmeasured velocities[J]. Journal of Marine Science and Technology， 2020， 26： 395-407. DOI： 10.1007/s00773-020-00744-3.

[11]LAPIERRE L， SOETANTO D. Nonlinear path-following control of an AUV[J]. Ocean Engineering， 2007， 34： 1734-1744. DOI： 10.1016/j.oceaneng.2006.10.019.

[12]LAPIERRE L， JOUVENCEL B. Robust nonlinear path-following control of an AUV[J]. IEEE Journal of Oceanic Engineering， 2008， 33（2）： 89-102. DOI： 10.1109/JOE.2008.923554.

[13]周佳加， 严浙平， 贾鹤鸣， 等. 改进规则下自适应神经网络的UUV水平面路径跟随控制[J]. 中南大学学报（自然科学版）， 2014，

45（9）： 3021-3028.

[14]边信黔， 程相勤， 贾鹤鸣， 等. 基于迭代滑模增量反馈的欠驱动AUV地形跟踪控制[J]. 控制与决策， 2011， 26（2）： 289-292， 296. DOI： 10.13195/j.cd.2011.02.132.bianxq.024.

[15]霍宇彤， 郭晨， 于浩淼. 欠驱动AUV三维路径跟踪RBF神经网络积分滑模控制[J]. 水下无人系统学报， 2020， 28（2）： 131-138. DOI： 10.11993/j.issn.2096-3920.2020.02.003.

[16]高剑， 李勇强， 李璐琼， 等. 基于航路点跟踪的AUV回收控制[J]. 火力与指挥控制， 2013， 38（8）： 103-106.

[17]王宏健， 陈子印， 边信黔， 等. 欠驱动水下航行器三维直线航迹跟踪控制[J]. 控制理论与应用， 2013， 30（4）： 443-453. DOI： 10.7641/CTA.2013.20359.

[18]WANG N， SUN Z， JIAO Y H， et al. Surge-heading guidance based finite-time path-following of underactuated marine vehicles[J]. IEEE Transactions on Vehicular Technology， 2019， 68（9）： 8523-8532. DOI： 10.1109/TVT.2019.2927893.

[19]WANG N， KARIMI H R， LI H Y， et al. Accurate trajectory tracking of disturbed surface vehicles： a finite-time control approach[J]. IEEE/AEME Transactions on Mechatronics， 2019， 24（3）： 1064-1074. DOI： 10.1109/TMECH.2019.2906395.

[20]REPOULIAS F， PAPADOPOULOS E. Planar trajectory planning and tracking control design for underactuated AUVs[J]. Ocean Engineering， 2007， 34： 1650-1667. DOI： 10.1016/j.oceaneng.2006.11.007.

（编辑 贾裙平）

收稿日期： 2020-11-18

修回日期： 2021-06-25

基金項目： 国家自然科学基金（51879023）;海洋防务技术创新基金（JJ-2020-701-02）

作者简介：

滕建平（1994—），男，山东烟台人，硕士研究生，研究方向为海上无人系统，（E-mail）tengjp@163.com;