考虑补货优先级的服装横向转运库存优化

范雨涵 宋鑫 高银萍 苌道方

摘要：针对需求不确定带来的服装产品库存失衡问题，构建由一个区域仓和多个采用直营店营销模式的零售商组成的横向转运库存优化模型。引入补货优先级来描述零售商的服务水平。在零售商服务水平约束下，寻求各零售商转运和补货的供应方案，实现系统运营成本最小化、服务水平下限最大化的目标。采用改进粒子群优化算法求解模型。通过仿真实例对模型的有效性进行验证。结果显示，执行横向转运策略后，系统运营成本平均降低39.5%，服务水平平均增加15.5%。研究表明，该方法不仅能够提高补货决策的经济性、提升区域零售商的整体服务水平，还可以解决零售商库存不均衡问题，有利于提高横向转运在服装领域的适用性。

关键词：

库存优化; 横向转运; 补货优先级; 服务水平; 粒子群优化算法

中图分类号：  F253.4

文献标志码：  A

Inventory optimization of apparel lateral transshipment

considering replenishment priority

FAN Yuhan， SONG Xin， GAO Yinping， CHANG Daofang

（Institute of Logistics Science & Engineering， Shanghai Maritime University， Shanghai 201306， China）

Abstract：

In view of the apparel inventory imbalance problem caused by demand uncertainty， the paper builds a lateral transshipment inventory optimization model composed of a regional warehouse and multiple retailers using the directly-managed store marketing model. The replenishment priority is introduced to describe the service level of retailers.Under the constraint of the service level of retailers， the supply scheme of the transshipment and replenishment of each retailer is sought to achieve the goal of minimizing the system operation cost and maximizing the lower limit of the service level.The model is solved by an improved particle swarm optimization algorithm.The effectiveness of the model is verified by simulation examples.The results show that， after implementing the lateral transshipment strategy， the system operation cost decreases by 39.5% on average， and the service level increases by 15.5% on average.The study shows that， this method can not only improve the economy of replenishment decisions and improve the overall service level of regional retailers， but also solve the problem of retailers’ inventory imbalance， which helps to improve the applicability of lateral transshipment in the clothing field.

Key words：

inventory optimization; lateral transshipment; replenishment priority; service level; particle swarm optimization algorithm

0 引 言

受季節、流行趋势、地理环境等因素影响，服装产品表现出需求不确定性强、生命周期短等特点。基于这些特点，服装产品的补货量往往难以预估，库存不均衡问题时有发生。一些服装企业考虑效仿其他行业的先进库存管理经验，以解决库存不均衡问题。横向转运因其在解决汽车零部件库存协调问题上的成功实践，逐渐步入大众视野。横向转运指在不影响供货零售商正常销售的情况下，用其库存冗余填补附近缺货零售商的库存空位，满足缺货零售商补货需求的库存管理策略。横向转运不仅能够有效解决库存不均衡问题，在成本和需求响应速度方面也表现出一定的优越性。因此，越来越多的服装企业将横向转运视为解决库存不均衡问题的有效手段。

实际上，横向转运早就引起了国内外学者的广泛关注。1989年，TAGARAS[1]对基于两点补货模式的横向转运进行了深入研究，发现转运可以降低系统成本，提高系统服务水平。而后，SLIKKER等[2]研究了统一订货、需求共享状态下横向转运的利益博弈问题，结果表明合作模式下的收益明显优于单干模式下的收益。FENG等[3]在两点补货模式的基础上对转运情景做了进一步细化，衍生出应急型横向转运和预防型横向转运两种策略。孙凌等[4]、宋乃绪[5]、杨璐等[6]将转运与订货、选址结合，发现转运不仅可以降低成本，还能提高供应网络抗风险能力，进一步推动了转运的发展。

为了让转运策略更好地落地，一些学者开始研究转运策略的实施过程。RUDI等[7]延续两点补货模式下的转运策略研究，探讨不同库存表现时转运量和转运成本的计量问题，细分了转运规则。KUTANOGLU等[8]、张秀丽[9]、戢守峰等[10]通过对服务水平的刻画，研究了服务水平限制下横向转运的决策过程。许民利等[11]考虑了等待时间对备件转运的影响，构建了基于等待时间和服务限制的备件库存模型。HU等[12]以快时尚服装企业为例，设计了零售联盟状态下多库存点转运的决策支持系统。GALLIEN等[13]以ZARA公司为研究背景，建立了不确定需求下允许转运的库存模型。NADERI等[14]以服装产品为例，探讨了转运过程对人力和库存的占用问题，据此建立了库存容量限制下的转运策略。万鹏等[15]考虑备件产品的随机缺陷对转运决策的影响，研究了具有随机缺陷率产品的多点库存管理问题。徐琪等[16]探讨了转运价格对库存和利润的影响，但缺乏对具体转运策略、具体实施操作的论证。

综上所述，横向转运的优点已在研究和实践中得到认证，但在转运实施过程的研究方面，多集中于服务水平、交付时间对决策的限制，研究不够深入。此外，在服务水平的刻画方面，现有研究多着眼于需求满足率、交付时间对服务水平的影响，刻画方式较为单一，而实际上转运决策需考虑多方因素，如销售能力、品牌战略等，具有较高的复杂度和灵活性。因此，本文从实际出发，以最小化系统运营成本和最大化系统服务水平下限为目标，通过引入补货优先级，平衡企业战略、销售能力和需求满足率的关系，完成服务水平的深度刻画，在此基础上建立服装产品多点转运的库存优化模型。

1 问题描述

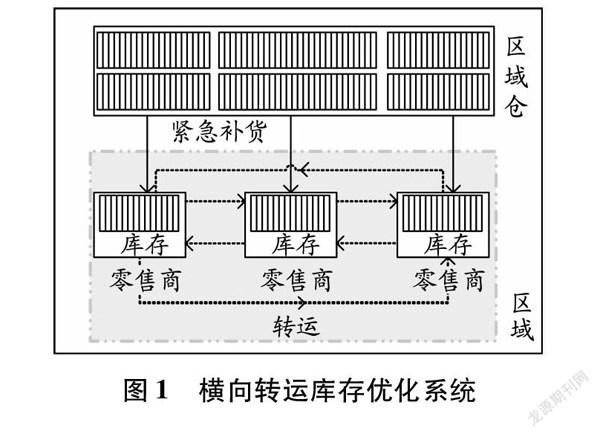
考虑一个区域内由一个区域仓和多个采用直营店营销模式的零售商组成的横向转运库存优化系统，见图1。企业初始配货完成后，随着销售的不断进行，部分零售商库存到达库存控制点，无法满足市场需求，急需产品供应，此时，横向转运策略在系统内触发，具体执行策略如下：（1）在市场需求预估的前提下，考虑策略执行的效率，系统会对各个零售商进行库存盘点，确定各零售商的缺货量或库存冗余量。（2）计算零售商的补货优先级，进而确定零售

商的服务水平现状。（3）根据上述计算结果，执行横向转运库存优化模型，优先确定调入对象、调出对

象和转运数量，当横向转运无法满足缺货零售商的需求时，采用紧急补货维持产品供应稳定。（4）根据横向转运策略执行结果，零售商进行产品打包、配送和验收，物流中心更新库存信息。

2 模型建立

2.1 模型假设

考虑到横向转运策略实施的实际情景，做如下假设：（1）由于直营店为企业所有，产品转运相当于物资在企业内部流动，库存信息、销售利润归企业所有，不涉及零售商之间的信息协调和利润分配。（2）由于零售商所处地理位置的差异，各零售商面向的市场相互独立，不存在需求竞争。（3）由于零售商处于同一区域，零售商之间距离相对较小，运输耗费的转运时间可忽略不计。（4）转运过程涉及产品的包装和运输，必然会耗费一定的人力和空间，因此，每个供货零售商一次仅允许援助一个零售商;同时，考虑到成本和服务水平的限制，一个零售商可接收多个零售商的供给。（5）为保证零售商正常的采购和销售，避免囤貨套利，假设需求满足方式的优先级依次为直接满足、转运满足、紧急补货满足。当需求到达时，零售商优先采用自有库存满足需求;当自有库存无法满足需求时，优先采用横向转运满足;若转运后仍无法满足需求，则采用成本较高的紧急补货来满足。

2.2 模型参数与变量

集合：零售商集合N={1，2，…，n}，i，j∈N。

参数：si为零售商i的初始库存量;hi为零售商i的库存控制点;ki为零售商i的当前库存量;di为截至销售季末，零售商i的预计市场需求;ti为产品在零售商i的上架天数;vi为产品在零售商i的平均历史销售速度，

v′i为vi归一化后的结果;pi为零售商i的初始库存在区域内初始库存中的占比，

p′i为pi归一化后的结果;cs为单位产品的库存持有成本;cl为单位产品的转运成本;

cb为单位产品的缺货成本;ce为单位产品的紧急补货成本;ri为零售商i的补货优先级;

wv为销售速率因子在补货优先级中的权重;wp为企业战略因子在补货优先级中的权重;α为系统给定的零售商的服务水平;εi为零售商i的服务水平现状。

决策变量：xij表示零售商i向零售商j转运的决策变量，xij∈{0，1}，若产品从零售商i向零售商j转运，

则xij=1，否则xij=0;lij表示零售商i向零售商j转运的库存量;ei表示零售商i需要区域仓紧急供应的补货量。

2.3 服务水平刻画

式（7）和（8）为目标函数：式（7）表示采用横向转运策略后，保证由系统内的库存持有成本、转运成本、预计缺货成本和紧急补货成本组成的运营成本最低;式（8）表示转运完成后，保证零售商整体的服务水平下限最高。式（9）～（19）为约束条件：式（9）表示零售商j接收的转运量不能超过其预计的市场需求;式（10）考虑到初始库存容量限制，零售商j接收的库存不能超过初始库存量;式（11）表示在满足自身市场需求且不触及库存控制点的情况下，零售商i可以向其他零售商外调的货物数量;式（12）考虑到转运会耗费一定人力和库存空间，供货零售商一次最多供应一家零售商;式（13）表示零售商j同时可以接收的系统内供货零售商的数量上限;式（14）表示系统对零售商i的服务水平限制;式（15）表示为保证零售商需求满足方式的优先级依次为直接满足、转运满足、紧急补货满足，本文在需求满足成本方面进行了控制，要求零售商库存持有成本低于转运成本，转运成本低于缺货成本，缺货成本低于紧急补货成本;式（16）确定供货、接收货物的零售主体;式（17）表示转运执行后，零售商i从区域仓紧急补货的数量不能低于服务水平限制下的实际需求量;式（18）表示xij为0-1变量，xij=1表示零售商i向零售商j发出转运请求，xij=0表示零售商i不接受零售商j的转运请求;式（19）考虑到指标的现实意义，

参数取值均为非负整数。

3 横向转运库存优化模型的粒子群优化算法设计

由于问题本身属于带约束的非线性离散混合整数规划模型，传统数学规划算法在该问题的求解方面受到了限制，模型求解比较复杂。同时，模型主要应用于实践领域，更注重解决问题的时效性，精确性要求不高，故采用智能搜索算法更为合适。相较于其他智能优化算法，粒子群优化算法＼[17＼]寻优能力强，收敛速度快，能够快速得到较好的解，适用于本文服装横向转运库存优化模型的求解。因此，本文采用粒子群优化算法求解，并对算法进行改进。

3.1 编码方案设计

3.2 适应度函数设计

本文建立的模型是一个多目标优化模型，在求解过程中需整合成一个适应度函数。由于目标是保证成本经济性和高服务水平，且两个目标函数存在较大的量纲差异，本文在将服务水平下限最大转化成其倒数最小的基础上，使用控制系数

ρ1调节目标函数间的量纲差异，实现目标函数的整合，得到适应度函数：

min FF=ρf1/f2

式中：ρ=nρ1，n为零售商数量。

3.3 位置与速度更新方案

在初始化粒子的种群后，粒子会在寻优空间内以一定的速度飞行，其间经过粒子本身所经历过的

历史最优位置

xpb和粒子种群目前所找到的历史最优位置xgb。在每一次迭代过程中，通过跟踪个体极值

xpb和总体极值xgb来更新每个粒子的位置和速度。由于缺货零售商不参与外调服务，缺货零售商的决策结果为零向量，如果单纯依赖传统离散二进制粒子群优化算法（discrete binary particle swarm optimization algorithm，BPSO）迭代更新，则需要大量的粒子位置、速度纠偏工作，增加算法的计算复杂度。参照田军等＼[18＼]提出的变换思路，采用如下方法更新粒子。

式中：表示速度的加法，在速度交换数顺序不变的情况下，取两个速度中交换数的并集;⊙表示位置间的减法，通过逐一比较两个位置的分量，确定由不同分量构成的交换数，即速度;表示位置与速度的加法，根据粒子速度的方向，按照交换数顺序做2-opt运算;w1为惯性权重，表示粒子在搜索空间内飞行的动力;

c1和c2为学习因子，表示粒子对自身经历和种群历史的重视程度;t为迭代次数;r1和r2为随机因子。

结合横向转运库存优化模型的特点，对转运量进行适度控制，即在粒子飞出寻优空间时对粒子位置和速度进行修正。根据景明阳＼[19＼]对粒子位置修正策略的研究，提出基于横向转运库存优化模型的粒子位置和速度修正策略。考虑每个供货零售商一次只能为一个缺货零售商供货，补货优先级高的零售商优先转运更有利于提高整体水平。因此，确定供货对象后，在保证转运决策不变的情况下，考虑供货零售商的库存余量、缺货零售商的需求量和最大库存量限制，在粒子飞出边界的供货点中，优先将补货优先级高的供货零售商供货量上调至最高。若迭代过程中粒子飞出边界，则需从缺货零售商的角度，盘查粒子飞出边界的情况。假设第n+j列有m个点飞出边界，缺货零售商j有补货需求dj-kj+hj，在飞出边界的m个供货点中，若零售商i的补货优先级最高，则粒子位置X中的点xi，n+j调至min（ki-di-hi，（dj-kj+hj）-m+1，sj-kj-m+1），其余异常供货点更新为1，同时更新vi，n+j，更新公式vi，n+j=rand（）·vi，n+j，其余各点保持不变。

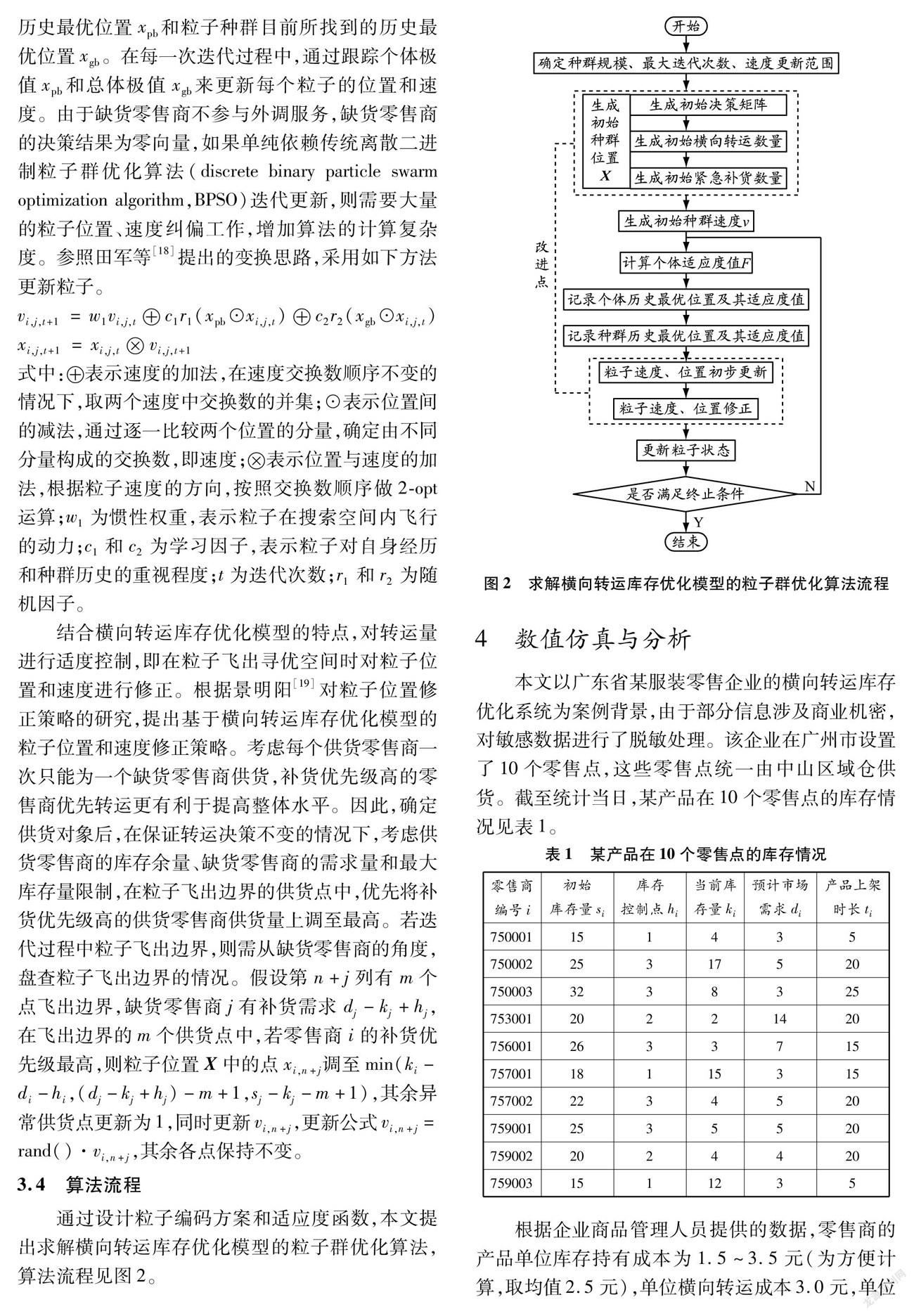
3.4 算法流程

通过设计粒子编码方案和适应度函数，本文提出求解横向转运库存优化模型的粒子群优化算法，算法流程见图2。

4 数值仿真与分析

本文以广东省某服装零售企业的横向转运库存优化系统为案例背景，由于部分信息涉及商业机密，对敏感数据进行了脱敏处理。该企业在广州市设置了10个零售点，这些零售点统一由中山区域仓供货。截至统计当日，某产品在10个零售点的库存情况见表1。

根据企业商品管理人员提供的数据，零售商的产品单位库存持有成本为1.5～3.5元（为方便计算，取均值2.5元），单位横向转运成本3.0元，单位短缺成本4.0元，单位紧急补货成本5.0元。设置销售速率因子权重wv=1.1，企業战略因子权重

wp=1.5。此外，本文在Windows系统，运行内存为8 GB的环境下，

使用Python 3.3.3编程进行求解。

4.1 服务水平敏感性分析

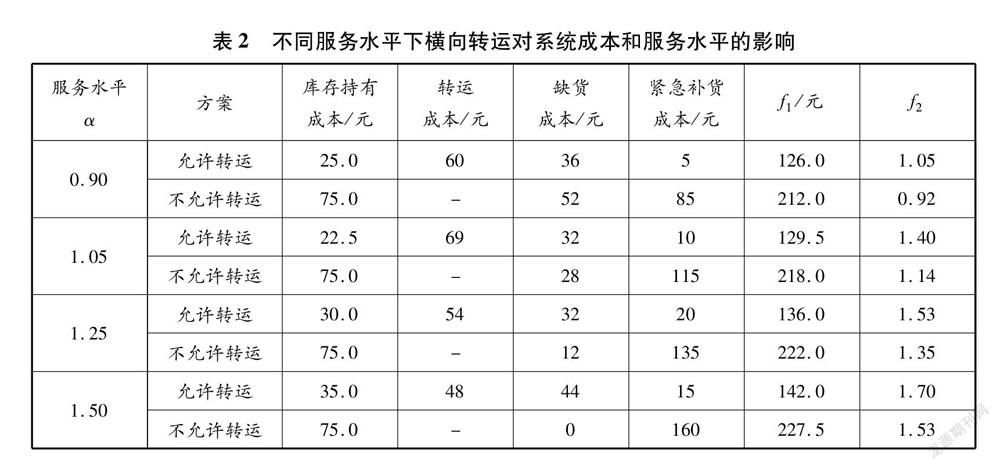
本文研究服务水平α分别为0.90、1.05、1.25、1.50时横向转运对系统运营成本和服务水平的影响，得到不同服务水平下两种方案的数据表现，见表2。

由表2可知：相较于不允许转运，采用横向转运虽然会增加一定的转运成本，但在控制库存持有成本和紧急补货成本方面效果显著，单项成本降幅均超过60.0%，系统运营成本平均降低了39.5%;在服务水平方面，采用横向转运的系统服务水平更高，系统服务水平下限平均增加15.5%，优化效果显著。

4.2 算法分析

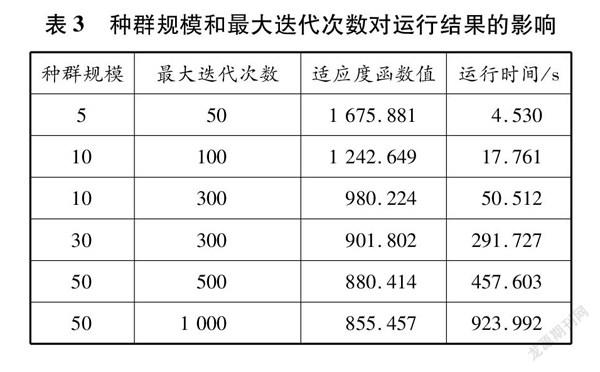
为进一步分析算法的效果，以种群规模和迭代次数为参数，分析不同种群规模和最大迭代次数下，算法的搜索能力和收敛能力。沿用田雨波＼[20＼]的实验方法，对粒子受社会知识和个体认知的影响赋予同样的权重，将学习因子

c1和c2设定为2，计算结果见表3。表3中，适应度函数值和运行时间为算法随机执行50次的均值。

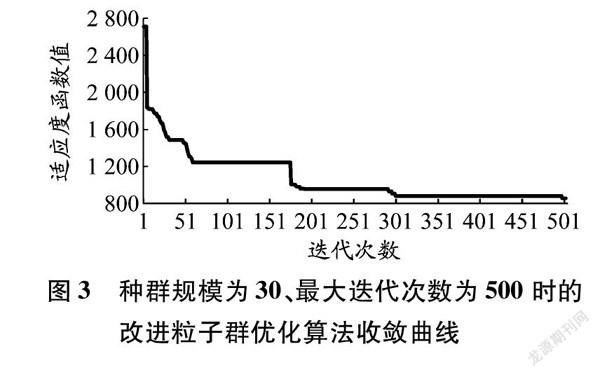
对比分析各组实验结果，当初始种群规模为30，最大迭代次数为300时，算法在计算效率和实验结果方面表现较好。为保证求解效率和求解精度，进一步分析收敛曲线，见图3。由图3可知，算法在迭代300次时已达到较优解，后续虽寻得较优解，但优化效果不够明显，且耗时较长。因此，本文选用种群规模为30，最大迭代次数为300作为算法的寻优阈值。

5 结束语

以一种服装产品为例，研究了一个区域仓和多个零售商组成的横向转运库存优化系统，提出横向转运策略下系统的最优供应方案。首先，通过将补货优先级引入服务水平刻画过程，均衡不同零售商在需求满足率方面的感知差异，消除转运过程中不均衡调度的影响。其次，在建模过程中，不仅考虑系统运营成本，还兼顾各个零售商的服务水平限制，为服装产品横向转运库存优化问题提供了研究思路，具有较强的实际意义。最后，基于横向转运库存优化系统的特点，设计了“离散-连续混合编码”的粒子群优化算法，通过对比不同种群规模和最大迭代次数下的实验结果，验证了模型的有效性。应当指出，本文仅对单种服装产品的横向转运库存优化问题进行了研究，今后还可以向多种服装产品的横向转运库存优化方向拓展，扩大模型的适用范围。

参考文献：

[1]TAGARAS G. Effects of pooling on the optimization and service levels of two-location inventory systems[J]. IIE Transactions， 1989， 21（3）： 250-257. DOI： 10.1080/07408178908966229.

[2]SLIKKER M， FRANSOO J， WOUTERS M. Cooperation between multiple news-vendors with transshipments[J]. European Journal of Operational Research， 2004， 167： 370-380. DOI： 10.1016/j.ejor.2004.03.014.

[3]FENG P P， WU F， FUNG R Y K， et al. Evaluation of two transshipment policies in a two-location decentralized inventory system under partial backordering[J]. Transportation Research Part E， 2018， 118： 207-224. DOI： 10.1016/j.tre.2018.07.010.

[4]孙凌， 罗长远， 吕真. 基于延迟转运的维修备件库存模型[J]. 计算机工程与应用， 2017， 53（19）： 265-270. DOI： 10.3778/j.issn.1002-8331.1604-0160.

[5]宋乃绪. 中断风险下考虑横向转运的分销网络模型研究[D]. 青岛： 青岛理工大學， 2018.

[6]杨璐， 陈彦如， 杨洁. 考虑缺货和产品缺陷的联合补货模型[J]. 管理工程学报， 2018， 32（4）： 195-203. DOI： 10.13587/j.cnki.jieem.2018.04.024.

[7]RUDI N， KAPUR S， PYKE D F. A Two-location inventory model with transshipment and local decision making[J]. Management Science， 2001， 47（12）： 1668-1680. DOI： 10.1287/mnsc.47.12.1668.10235.

[8]KUTANOGLU E， MAHAJAN M. An inventory sharing and allocation method for a multi-location service parts logistics network with time-based service levels[J]. European Journal of Operational Research， 2007， 194（3）： 728-742. DOI： 10.1016/j.ejor.2007.12.032.

[9]张秀丽. 考虑转运策略和服务水平约束的三级供应链库存共享模型研究[D]. 沈阳： 东北大学， 2015.

[10]戢守峰， 万鹏， 孙琦， 等. 库存共享和服务水平限制下三级分销网络侧向转运模型与算法[J]. 中国管理科学， 2016， 24（12）： 72-81. DOI： 10.16381/j.cnki.issn1003-207x.2016.12.009.

[11]许民利， 孙彩群. 基于等待时间限制的服务备件多点转运库存模型研究[J]. 山东大学学报（理学版）， 2010， 45（3）： 61-65.

[12]HU Z H， YU X K. Optimization of fast-fashion apparel transshipment among retailers[J]. Textile Research Journal， 2014， 84（20）： 2127-2139. DOI： 10.1177/0040517514538695.

[13]GALLIEN J， MERSEREAU A J， GARRO A， et al. Initial shipment decisions for new products at Zara[J]. Operations Research， 2015， 63（2）： 269-286. DOI： 10.1287/opre.2014.1343.

[14]NADERI S， KILIC K， DASCI A. A deterministic model for the transshipment problem of a fast fashion retailer under capacity constraints[J]. International Journal of Production Economics， 2020， 227： 107687. DOI： 10.1016/j.ijpe.2020.107687.

[15]万鹏， 戢守峰， 宋乃绪. 具有随机缺陷率产品的多点转运库存优化模型[J]. 计算机集成制造系统， 2020， 26（9）： 2561-2572. DOI： 10.13196/j.cims.2020.09.025.

[16]徐琪， 高晓晴. 共享库存下双渠道零售商最优订购与转运价格决策[J]. 工业工程与管理， 2020， 25（1）： 110-117， 126. DOI： 10.19495/j.cnki.1007-5429.2020.01.013.

[17]KENNEDY J， EBERHART R. Particle swarm optimization[C]//International Conference on Neural Networks. IEEE， 1995： 1942-1948.

[18]田军， 马文正， 汪应洛， 等. 应急物资配送动态调度的粒子群算法[J]. 系统工程理论与实践， 2011， 31（5）： 898-906. DOI： 10.12011/1000-6788（2011）5-898.

[19]景明陽. 基于离散粒子群算法的师资配置模型研究[D]. 西安： 西安理工大学， 2018.

[20]田雨波. 粒子群优化算法及电磁应用[M]. 北京： 科学出版社， 2014： 23-25.

（编辑 贾裙平）

收稿日期： 2020-12-15

修回日期： 2021-02-01

作者简介：

范雨涵（1995—），女，山东济宁人，硕士研究生，研究方向为物流系统优化，（E-mail）18342962848@163.com;

宋鑫（1993—），男，安徽池州人，博士研究生，研究方向为供应链设计与运营、物流系统运作与优化，（E-mail）351967213@qq.com;

高银萍（1994—），女，江苏泰州人，博士研究生，研究方向为港口运营与优化，（E-mail）gaoyinping@stu.shmtu.edu.cn;

苌道方（1978—），男，河南新乡人，教授，博导，博士，研究方向为供应链设计与运营、物流系统运作与优化，

（E-mail）dfchang@shmtu.edu.cn