金红石型二氧化钛薄膜热导率的数值模拟
白素媛, 白容榕, 吴 可
(辽宁师范大学 物理与电子技术学院,辽宁 大连 116029)
作为禁带宽度达到3.2 eV的无机半导体多功能材料,二氧化钛有着无毒、成本低、抗腐蚀、高光催化活性等特点,且热、物理、化学性质稳定,被广泛应用于染料敏化太阳能电池、介敏材料、光学催化剂、气体传感器、电致变色器件等研究方面.作为自然界中二氧化钛存在的形式之一,金红石拥有良好的光散射和光反射性能,折射率高,无毒,无论是强酸还是强碱环境中都具有化学惰性,因此是最稳定的热力学材料.尽管金红石与锐钛矿相相比具有较低的电子迁移率,但这些特性使其在光电应用方面也具有吸引力,如太阳能电池[1].
作为染料敏化太阳能电池的重要组成器件之一,二氧化钛的散热效果对太阳能电池的光电转化效率有着显著影响,因此二氧化钛作为热电材料受到了人们的广泛关注.Maekawa等人通过金属有机化学气相沉淀法合成了不同形貌的二氧化钛薄膜,并研究其微观结构对薄膜热导率产生的影响[2].Kim等人使用3ω法测定了直流磁控溅射法制备的4种二氧化钛薄膜在80 K到室温温度范围内的导热系数[3].Donovan等人通过分析模型进一步了解了二氧化钛热传输的趋势,并确定了本征点缺陷对金红石型二氧化钛热传输的影响[4].热导率的测量具有重要意义,因为它包含有关材料微观结构的信息,有助于分析各种器件的性能.随着理论与计算模拟的发展,分子动力学(MD)方法已经逐渐成为模拟预测一些难以通过实验方法测量的材料的重要手段,特别是在纳米尺度上,MD方法为预测导热性、揭示影响薄膜导热机制和因素等方面提供了一种很有前景的选择.Fujiwara等人基于平衡分子动力学和非平衡分子动力学计算研究了纳米流体的热导率,并阐述了热导率变化的机制[5].本研究小组利用分子动力学方法,基于COMPASS力场,测量了低维纳米材料室温下的导热率[6].Momenzadeh等人采用平衡分子动力学方法,确定了金红石型二氧化钛的晶格导热系数[7].尽管如此,与众多实验方法研究相比,利用MD方法对二氧化钛热导率进行数值模拟的研究工作较少,因此本文借助MD方法,通过二氧化钛薄膜的厚度和氧空位浓度这些因素的改变,计算分析其对薄膜热导率的变化关系.
1 理论基础
1.1 非平衡分子动力学方法(NEMD)
分子动力学计算模拟薄膜热导率主要有EMD和NEMD[8]两种方法.EMD即模拟体系在平衡状态下的热导率,其基于Green-Kubo方程.NEMD即对系统施加扰动,建立非平衡热传输过程,模拟非平衡导热,基于Fourier定律[9]计算求得热导率.因为现实中系统常常设有温度梯度,且具有不可逆热流,而通过NEMD可以对这种不可逆非平衡过程进行模拟.基于以上考虑,本文选择通过NEMD进行二氧化钛薄膜热导率的计算模拟.
1.2 系综
分子动力学模拟计算给出模拟体系的微观信息,通过统计物理学将微观状态下的相关参数转化为宏观性质,因此引入系综这一概念.常用的系综除了有微正则系综(NVE)、正则系综(NVT)、等压等焓系综(NPH),还有等温等压系综(NPT).其中,在NVE系综里,粒子沿着相空间中的恒定能量轨道演化,体系中的粒子数N和体积V恒定,与外界不产生任何能量交换,不需要重新控制体系的能量,因此本文在对金红石型二氧化钛薄膜的研究中选用微正则系综.
1.3 COMPASS势函数
分子动力学模拟中,建立正确的势函数模型是必要前提,其用来描述粒子间的相互作用,直接关系到模拟的准确性和正确性,因此选择合适的势函数至关重要.其中Buckingham势函数、Morse势函数、Lennard-Jones势函数等两体势应用较为广泛,常见的多体势有Stillinger-Wab势函数、Tersoff势函数、MEAM势等,此外还有力场.常见的力场有DERIDING力场、UNIVERSAL力场、COMPASS力场.本文采用了COMPASS力场[10]对金红石型二氧化钛薄膜进行模拟计算,作为凝聚态优化分子势,其势函数形式可表达为
E=Eb+Eθ+Eφ+Eχ+Ecross+Eij+Eelec=
(1)
其中,k、H、V、A、B为力常数,b为键长,θ为键角,φ为二面角,ε为能量参数,rij为原子与原子间距,q为电荷量.由键合项和非键合项构成了力场能量.其中键伸缩能、键角弯曲能、键钮转能、键角面外弯曲能及相互耦合能为键合项.范德华力、库伦力以及原子对之间的相互作用力为非键合项.
2 模拟过程与结果
在系统中建立金红石型二氧化钛基本单元,其结构如图1所示,根据周期性边界条件,选取的截断半径不宜过小,其原因是为了防止系统中粒子间相互作用,且模拟系统中粒子过多会对计算机运行速度产生一定的影响.基于以上考虑,本文在建立超晶胞时分别在X、Y方向上选取4个基本单元,在厚度Z方向上选取24个基本单元,如图2所示为金红石二型氧化钛超晶胞计算模型.

图1 金红石型二氧化钛基本单元结构模型

图2 金红石型二氧化钛4×4×24计算模型
2.1 膜厚对二氧化钛薄膜热导率的影响
在进行非平衡分子动力学模拟时,需要判断模拟体系是否达到稳态,本文采用观察系统中Z方向上的温度分布曲线是否光滑来进行判断.以计算模型4×4×48(即厚度7.10 nm)为例进行初步模拟,体系温度为300 K,时间步选取为1.0 fs,如图3所示分别为模拟步数50万步和250万步时的温度分布曲线.经两图比较可知,随着计算步数增多,温度分布曲线逐渐光滑,可以判断系统在250万步计算后达到了平衡状态.

图3 不同计算步数下各层温度分布曲线
表1为室温300 K下不同膜厚的二氧化钛薄膜的热导率,由表1能够观察到薄膜厚度范围在5.92~8.29 nm内变化的二氧化钛薄膜,其热导率在1.899~2.522 Wm-1K-1之间.图4为二氧化钛薄膜不同厚度下的热导率变化曲线图,由此图可看出,其热导率随着薄膜厚度的增大而增大,两者接近于线性变化,图像呈示出显著的尺寸效应.

表1 不同厚度的二氧化钛薄膜热导率的计算结果

图4 热导率与薄膜厚度的变化曲线
根据德拜理论可得出晶格热导率为
(2)
其中,c为单位体积比热容,v为声子平均速度,leff为有效声子平均自由程.由式(2)可以看出,当膜厚d远超过声子平均自由程l时,声子与边界进行碰撞的概率很小,声子的平均自由程在碰撞过程中可保持恒定不变,热导率也因此保持一定值;当d与l相等或d小于l时,声子与边界进行碰撞的概率变大,此时需要考虑到散射作用对热量传输的影响,因此声子的平均自由程在碰撞过程中变小,热导率也随之变小;当膜厚d远小于声子平均自由程l时,热导率随膜厚变小而变小这一特点越来越明显.影响声子平均自由程的因素主要是声子的散射,如声子与声子之间的散射,边界对声子的散射等.这些散射机制对材料的传热性能有显著影响,因此,当膜厚d由5.92 nm增长到8.29 nm并远小于声子平均自由程l时,声子边界散射作用减小,热导率随之增加,且热导率与薄膜厚度接近于线性变化,表现出鲜明的尺寸效应.
将本文模拟结果与该文献[7]进行对照,虽然所用计算模拟方法和膜厚范围不同,导致测得的热导率结果有所差别,但得到的变化趋势一致,由此可以看出本文模拟结果具有合理性.
2.2 浓度对空位缺陷型二氧化钛薄膜热导率的影响
现实中晶体总是存在一定数量的缺陷或瑕疵,而这种缺陷对材料的性质必然会造成一定的影响.通常人们认为二氧化钛中的缺陷对材料的性能具有负面影响,但研究表明,适当的缺陷在一些条件下可以使材料的性能得到改善,甚至会产生某些新功能.Yoon等人观察到含氧缺陷的锐钛矿型二氧化钛薄膜具有居里温度高达800 K的高温磁铁性[11].Sung等人研究了二氧化钛中氧空位梯度对双极型电阻式存储器切换方向的影响[12].Wang等人研究了含氧缺陷的二氧化钛可作为锂硫电池的新型功能主体[13].氧空位的存在使二氧化钛的电导性、铁磁性和光响应等性质发生明显变化,二氧化钛的热导率也可能受到氧空位的影响,其相关研究和文献却并不多,所以本文就氧空位浓度与金红石型二氧化钛薄膜热导率之间的变化关系进行相关模拟计算.
采用非平衡分子动力学模拟方法,将空位浓度定义为产生空位的原子数与模拟体系总原子数的比值.仍采用计算模型4×4×48(即厚度7.10 nm)来进行模拟,此时模拟体系中的总原子数为4 608个.在5组基本模型中分别随机抽取3、4、5、6、7个氧原子,空位浓度分别为0.065%、0.087%、0.109%、0.130%、0.152%,图5为空位缺陷结构示意图.经过模拟计算,在系统温度300 K下,氧空位浓度为0.109%的二氧化钛薄膜各层的温度分布曲线如图6所示.

图5 空位缺陷结构示意图
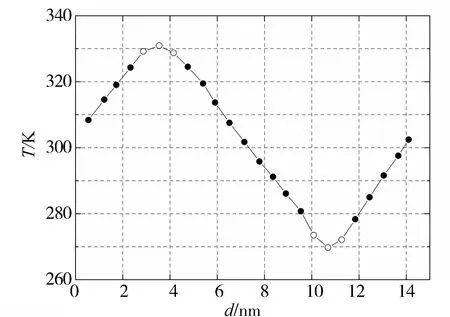
图6 空位浓度为0.109%的二氧化钛薄膜温度分布曲线
表2为二氧化钛薄膜在系统温度300 K下不同氧空位浓度时的导热系数,由表2可知氧空位浓度在0.065%~0.152%范围内变化的二氧化钛薄膜,其热导率在2.148~1.705 Wm-1K-1之间.图7为含氧空位缺陷的二氧化钛薄膜与氧空位浓度之间的变化曲线.可以看出,氧空位的存在使二氧化钛薄膜热导率下降,且热导率会随着氧空位浓度的增加而减小.晶体内热传递主要靠声子的散射来完成,由于晶体内有空位的存在,体系中出现声子与缺陷的散射,使得热导率随着声子平均自由程的减小而减小.文献[14]采用Tersoff势函数模拟了不同空位浓度下硅薄膜热导率的变化,得到空位缺陷使热导率降低与声子的散射有关,与本文研究结果相类似.

表2 不同空位浓度的二氧化钛薄膜热导率的计算结果

图7 热导率与空位浓度的变化曲线
3 结 论
本文在COMPASS力场下,基于NEMD方法,选用NVE系综对系统温度300 K下的金红石型二氧化钛薄膜热导率进行计算模拟.模拟结果表明:二氧化钛薄膜热导率随着薄膜厚度的增大而增大;当二氧化钛薄膜厚度不变时,热导率会随着氧空位浓度的增大而减小.应用德拜理论进行理论分析,同时对模拟计算结果与其他文献实验结果进行分析与比较,证实了本文模拟结果的可靠性和合理性,具有重要参考作用.
——以金红石为例

