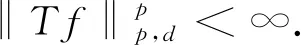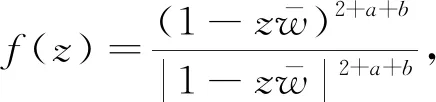一类积分算子的有界性
李 然, 姜宏升
(辽宁师范大学 数学学院,辽宁 大连 116029)
1 预备知识
2000年 Hedenmalm, Korenblum和Zhu[1]率先刻画一类积分算子的有界性.2006年Kures和Zhu[2]对单位球上一类积分算子的有界性进行完全刻画. 2015年Zhao[3]介绍单位球上舒尔检验, 并且应用此舒尔检验去证明单位球加权空间Lp(Bn,dμc)到Lq(Bn,dμd)上的一类积分算子的有界性.本文研究在单位圆盘加权空间Lp(D,dμc)到Lp(D,dμd)上一类积分算子的有界性.更多高维空间上积分算子的性质可以详见参考文献[4].令D表示复平面C中的单位圆盘, dA(z)表示D上的单位面积测度. 先介绍一类积分算子.
定义1.1对于任意实参数a,b,c,d,考虑两个积分算子:
和
考虑Ta,b,c,d,p和Sa,b,c,d,p在单位圆盘加权空间Lp(D,dμc)到Lp(D,dμd)空间上的有界性, 其中,1≤p<∞, dμc(z)=(1-|z|2)cdA(z),dμd(z)=(1-|z|2)ddA(z).
用〈·,·〉d表示Lp(D,dμd)中对偶积分对, 〈·,·〉c表示Lp(D,dμc)中对偶积分对, ‖·‖p,d表示Lp(D,dμd)中范数. 通过Banach共轭算子的定义, 得到
〈(Ta,b,c,d,pf),g〉d=〈f,[(Ta,b,c,d,p)*g]〉c,
进而有
因此得到从Lq(D,dμd)到Lq(D,dμc)的积分算子(Ta,b,c,d,p)*,


由于实参数a,b,c,d任意性,发现Ta,b,c,d,p的共轭算子(Ta,b,c,d,p)*和Ta,b,c,d,p的表达形式有如下关系.
引理1.2设q是p的共轭指数, 那么
(Ta,b,c,d,p)*=Tb-c,a+d,d,c,q.
引理1.3若f(z)为D上解析函数, 对于c>-1, 有
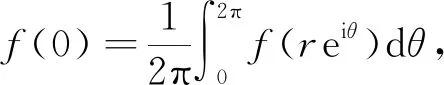
引理即证.
引理1.4[2]对任意-1<α<+∞和任意实数β,令

引理1.5[4]设X是测度空间,μ和ν是X上的正测度. 令T(x,y)是X×X上正可测函数,T是从Lp(X,dμ)到Lp(X,dν)的积分算子,


2 一类积分算子有界性
下面对于定义1.1中的积分算子讨论有界性.
定理2.1对于1≤p<∞, 且d≤c, 下面3个条件等价.
(1)Ta,b,c,d,p在Lp(D,dμc)上有界;
(2)Sa,b,c,d,p在Lp(D,dμc)上有界;
(3)ap+d>-1,c+1 证为了叙述方便, 令Ta,b,c,d,p=T,Sa,b,c,d,p=S. (2)⟹(1): 对于Lp(D,dμc)中任意函数f, 可知 (1)⟹(3): 因此, 选取测试函数f(z)=(1-|z|2)N, 令Np+c>-1, 因此f∈Lp(D,dμc). 根据引理1.3, 得到 因此ap+d>-1. 当p>1时, 由引理1.2、引理1.3和ap+d>-1,得到(b-c)q+c>-1.因此c+1 当p=1时,T*在L∞(D,dμd)上有界, 不等式转化为b>c. 选取测试函数f(z)=1. 根据引理1.2和引理1.3得到 根据引理1.5, 令α=a+d>-1,β=c-d, 因为d≤c, 所以β≥0, 即(T*f)(z)无界, 矛盾. 因此b>c. (3)⟹(2): 当p=1时, 根据Fubini定理, 得到 令α=a+d>-1,β=b-d>b-c>0, 由引理1.4得到 因此‖Sf‖1,d≤‖f‖1,c. 当p>1时, 令 (1) 将式(1)带入引理1.5, 得到 化简得 (2) 化简得 (3) 这里M为正数,q为p的共轭指数.