飞秒激光诱导Li2分子的电子-离子动力学的理论研究
洪许海, 刘浩然, 赵文杰, 郭 强, 谷 鑫
(辽宁师范大学 物理与电子技术学院,辽宁 大连 116029)
早在1917年,Einstein就在《辐射量子理论》一文中提出了激光产生的理论基础,但受制造水平和技术水平的限制,激光的受激辐射理论一直未得到有效的实验验证.直至1960年,由美国科学家Maiman研制的第一台红宝石固体激光器问世,受激辐射理论才得以实验验证.此后,激光技术取得飞速发展和快速突破,半导体激光器、氦氖激光器、二氧化碳激光器、YAG激光器相继问世.1991年,Spence等人利用自锁模技术产生了首束真正意义上的飞秒激光脉冲.此后,飞秒激光的各种参数纪录被不断刷新[1].由于飞秒激光具有脉宽更窄、峰值功率更高、聚焦区域更窄(微米数量级)等特性,被广泛应用于生产、生活、军事国防等领域.高功率的飞秒激光在材料加工、医学、加速器等领域有着广阔的应用前景[2].高功率的飞秒激光能够击穿大气,通过产生放电通道实现人工引雷,避免飞机、火箭、发电厂等重要设施因天然雷击造成损毁.飞秒激光在病变早期诊断、医学成像、生物活体检测、外科治疗等方面都发挥着不可替代的作用.飞秒激光可以有效加速电子,实现加速器规模压缩千倍以上.飞秒激光领域的飞速进展带动了非线性光学、变换光学、信息存储技术和激光生物物理学等新兴学科的快速发展.
飞秒激光具有多参数特征,通过联合优化时间、空间、频率、功率等参数,可以形成超快、超强等物理诱导条件,实现对作用体系电子-离子动力学的精准调控.近年来,科学家关注飞秒激光与原子、分子、团簇等物质相互作用过程中的电子-离子动力学现象,如:分子取向和形变、多光子离化、隧道电离、库仑爆炸、高次谐波产生等[3-5].飞秒激光为电子-离子动力学的调控提供了强有力的工具,使微观运动尺度上的超快过程探测成为现实,同时也对理论模型和方法提出了新的机遇和挑战.
在理论方面,含时密度泛函理论很好地平衡了计算量与计算精度,已被广泛用于处理量子多体系统,成为处理含时动力学问题的强有力工具[6].作为最简单的碱金属分子,Li2分子中的原子由非局域的单s电子和化学性质相对稳定的原子实组成,电子结构最为简单,为理论研究提供了理想的模型体系.本文选取轴对称的Li2分子为研究对象,采用实时间、实空间的含时密度泛函理论研究飞秒激光诱导的Li2分子的电子-离子动力学过程,通过调制激光频率、强度、极化方向等参数形成不同的激光诱导条件,研究激光与Li2分子相互作用过程中的响应偶极矩、离化电子数、总能量、原子实位移等物理量随时间变化的物理机制,本文的研究内容可为理解飞秒时间尺度上的电子-离子动力学提供一定的理论参考.
1 理论模型
含时密度泛函理论通过求解下面一组含时Kohn-Sham方程获得Kohn-Sham轨道波函数,含时密度泛函理论以含时密度作为信息载体,含时密度可表示为Kohn-Sham轨道波函数的模平方之和[7-8].
(1)
上式中的Kohn-Sham有效势VKS(r,t)一般由四项构成:
VKS(r,t)=Vion(r,t)+Vext(r,t)+VHartree(r,t)+Vxc(r,t),
(2)
第一项为原子实对价电子的势能,本文采用模守恒赝势描述[9],对Li2分子来说,Li原子的内壳层电子1s2与原子核构成相对稳定的原子实,两个2s电子为价电子;第二项为外势,即飞秒激光势场;第三项为电子与电子之间的Hartree势;最后一项为电子交换关联势,本文采用局域密度近似方法来描述电子交换关联势[10].
飞秒激光势场采用偶极近似描述:
(3)

(4)
上式中的T表示激光作用时间.
模拟过程采用实时间、实空间的开源软件包Octopus程序计算[11],计算参数设置如下:实空间模拟盒子是一个半径20 a.u.的球体,空间步长为0.35 a.u.,模拟盒子的球心位于坐标原点.Li2分子的基态结构通过几何构型优化获得,初始猜测构型的几何中心位于坐标原点,两原子实设置在x轴之上,通过体系最小总能量判据优化得到的两个锂原子坐标分别为(-2.565,0,0)和(2.565,0,0).除非特别声明,本文均采用原子单位制(a.u.).
2 结果与讨论
在激光势场的作用下,体系的电子-离子动力学行为强烈地依赖于系统响应频率与外场频率的匹配程度,而系统响应频率由系统的电子能级结构决定.本文的研究对象为轴对称的Li2分子,在之前的理论研究工作中[12],计算得到的沿Li2分子轴向的偶极响应频率为1.92 eV,垂直于轴向的偶极响应频率为2.52 eV,本文的激光参数设置如下:激光频率为Li2分子的偶极响应频率,激光场强度为1×1010、1×1011、1×1012和1×1013W/cm2,激光作用时间为10 fs,时间步长为0.4 a.u..鉴于Li2分子具有高度轴对称性,激光电场极化方向设置为平行于分子的轴向方向(x方向)和垂直于分子的轴向方向(y方向).
在不同极化方向、相同频率和场强的激光作用下,Li2分子的响应偶极矩、离化电子数和总能量随时间的变化如图1所示.在左图中,激光的电场极化方向为x方向,Li2分子产生的响应偶极矩明显溢出激光电场的包络线,表现出较强的共振行为,在激光作用结束时(10 fs),产生的离化电子数为0.48,此后系统继续经过20 fs的弛豫过程,在此过程中响应偶极矩仍以较大振幅振荡,在弛豫结束时(30 fs),离化电子数增至0.84.右图中的电场极化方向为y方向,产生的响应偶极矩的外包络与激光的包络线基本符合(只相差一个系数),表现出典型的非共振行为,在激光作用结束后,响应偶极矩振荡幅度较小,弛豫结束时的离化电子数为0.39,明显低于共振情况.在分子的两个典型方向上,电子的偶极响应频率不同,沿轴向方向上的偶极响应频率为1.92 eV,当该频率的激光沿轴向方向作用于Li2分子时,相较于垂直于轴的方向,体系从激光电场吸收更多的能量,能量的一部分使电子发生共振吸收能级跃迁,能量的另一部分转化为系统的内能,以电子的动能为主,电子运动速度的增大导致了响应偶极矩的大幅度振荡,使部分电子挣脱原子实的束缚成为自由电子.

图1 激光作用下Li2分子的响76666应偶极矩、离化电子数和总能量随时间的变化图中的虚线为激光电场振荡曲线,外部轮廓为激光电场的包络线,激光频率为1.92 eV,激光场强度为1×1012 W/cm2,激光电场极化方向分别为x方向(左图)、y方向(右图),竖直虚线表示激光作用结束时间
改变图1中的激光频率为2.52 eV,其他激光参数不变,计算得到Li2分子的响应偶极矩、离化电子数和总能量随时间的变化如图2所示.对比于图1,在不同极化方向的激光作用下分子产生的物理量对比情况发生了改变.此时,激光频率与垂直于分子轴向方向的电子偶极响应频率相匹配,当该频率的激光的极化方向沿垂直于轴向方向作用于分子时,相较于另一极化方向,体系吸收了更多的能量,使电子加速运动,对应的响应偶极矩发生较强的振荡,引起电子发生较强离化,在弛豫结束时,离化电子数达到0.93,接近一半的价电子发生离化,呈现出典型的共振行为.

图2 激光作用下Li2分子的响应偶极矩、离化电子数和吸收能量随时间的变化除激光频率变为2.52 eV以外,其他参数见图1说明
激光作用下Li2分子中的原子实x坐标的位移随时间的变化如图3所示.由于两原子实的位移大小几乎相同,在图中仅给出其中一个原子实的位移.在激光电场的作用下,分子不断吸收能量,体系中的电子自由度迅速响应激光电场,跟随激光电场的相位发生振荡,但由于离子自由度的响应速度滞后于电子自由度,在激光作用期间原子实的位移非常小.在激光作用结束后,体系在无外场的情况下进行弛豫,电子密度分布持续演化,并与原子实发生耦合,引起原子实产生位移.此外,随着激光场强度的增加,原子实的位移逐渐增大,特别是在激光场强度为1×1012W/cm2和1×1013W/cm2激光作用下,电子离化程度较强,体系中的剩余电子逐渐减少,电子密度的空间分布持续发生变化,对原子实的吸引力逐渐减弱,导致原子实的位移增大.当激光场强度增大至强场范围,体系甚至会发生库仑爆炸[13].

图3 激光作用下Li2分子中的原子实x坐标的位移随时间的变化
激光作用下Li2分子的总能量随时间的变化如图4所示.随着激光场强度的增加,体系的总能量在不断增大,特别是在频率2.52 eV、场强1×1013W/cm2的激光作用下,体系中的大部分电子发生离化,原子实的排斥能占体系总能量的主导地位,在弛豫结束时,体系的总能量甚至达到正值.在激光作用期间,体系的总能量随电场的相位变化发生振荡,在共振情况下,体系从激光场吸收的能量转化为电子跃迁能量和电子动能,在非共振情况下,体系从激光场吸收的能量主要转化为电子动能,在这两种情况下,电子都逐渐挣脱原子实的束缚成为自由电子,但在共振情况下的电子离化明显高于非共振情况,电子离化导致原子实之间的库仑排斥能迅速增加,在弛豫阶段,体系的总能量缓慢增加.从图中可以看到,除了在频率为2.52 eV、场强为1×1013W/cm2的激光作用下以外,体系在共振情况下的总能量明显高于非共振情况.
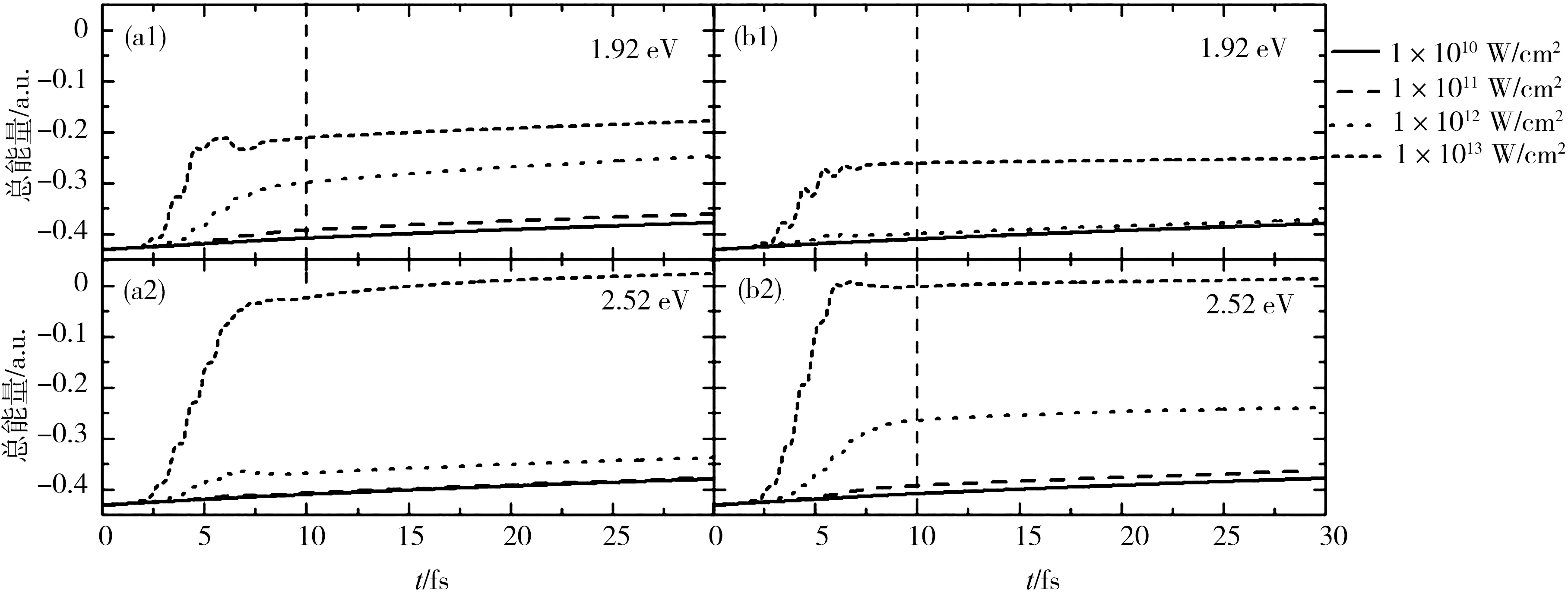
图4 激光作用下Li2分子的总能量随时间的变化
以频率为2.52 eV、场强为1×1012W/cm2的激光沿两个极化方向分别作用于Li2分子,在体系产生的响应偶极矩振荡最强位置附近分别选取5个具有代表性的时刻,画出体系z=0平面的电子密度振荡如图5所示.在上图中,激光极化方向沿分子的轴向,在下图中,激光极化方向垂直于分子的轴向,可以明显地观察到电子密度在原子实背景(两个黑色实心球)下的振荡行为,其中,图5(a3)和(b3)表示电子密度振荡至平衡位置,图5(a1)、(a5)、(b1)、(b5)表示电子密度振荡至最大位置,当电子密度振荡到最大位置时,部分电子云将挣脱原子实的束缚成为自由电子,离化的强弱程度由激光场参数决定.
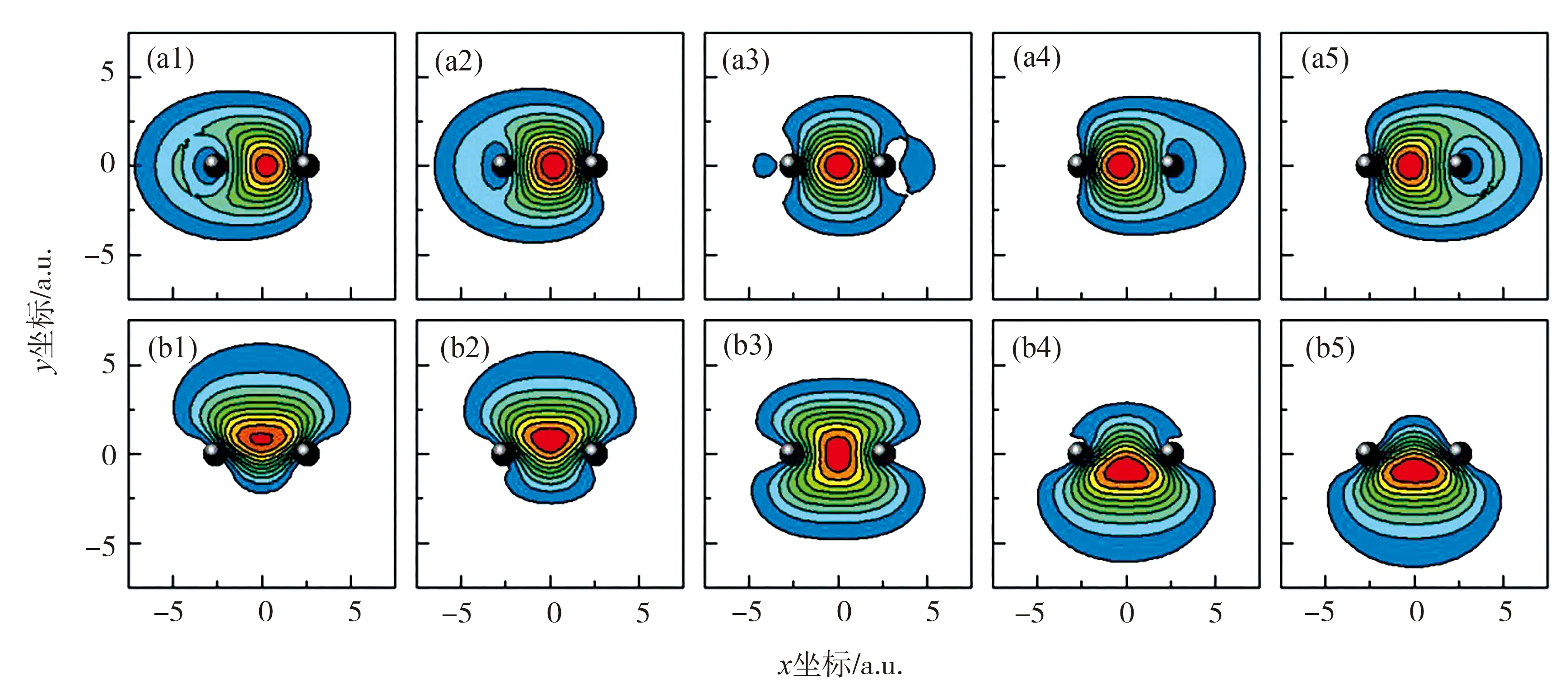
图5 激光作用下Li2分子的电子密度振荡
4 结 论
在激光势场的作用下,体系的电子动力学行为强烈地依赖于系统响应频率与外场频率的匹配程度.本文采用含时密度泛函理论模拟飞秒激光诱导Li2分子的电子-离子动力学过程,当激光参数(频率、极化方向)与Li2分子的偶极响应频率匹配时,体系吸收能量显著增加,体系的响应偶极矩明显溢出激光电场的包络线,在弛豫过程中,响应偶极矩仍以较大振幅振动,部分电子挣脱原子实的束缚成为自由电子,产生较强离化,呈现出典型的共振行为.随着激光场强度的增加,体系吸收能量增强,原子实的位移逐渐增大.在模拟过程中,通过对电子密度分布截图,观测到电子密度在原子实背景下的振荡行为.

