对接赋值非良策 化整为零乃妙方
——对一类数列求和问题的分析与思考
叶诚理 林新建 林品玲
(1.福建省福清第一中学 350300;2.福建省福清进修学校 350300)
以函数、导数为背景的数列求和取值范围问题,是近年来高考压轴题的常客.对非常规的数列求和问题学生往往束手无策,需要从数学思想方法的高度对问题进行化归转化、构造赋值,难度极高.那么,有没有比较自然的解题策略呢?下面举一道典型例题加以剖析.
1 试题呈现


(2)若不等式f(x)≥1在x∈[0,+∞)时恒成立,求实数a的取值范围;
2 命题意图分析
本题考查导数及其应用,旨在运用导数研究函数的单调性、不等式恒成立问题以及构造函数证明数列不等式的方法,综合性较强,考查学生分析问题和解决问题的能力,考查学生的数学抽象、直观想象和逻辑推理等核心素养.
3 解答难点剖析
本题难在第(3)问,对于这类出现在导数压轴题中的数列求和不等式问题,常见的解题套路是对接前面的函数不等式结论,对变量x有效赋值,结合对数运算,从而构造与结论相匹配的数列通项,利用数列求和的裂项相消法证得不等式.
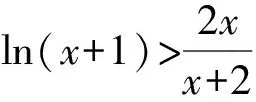
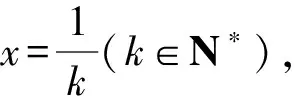

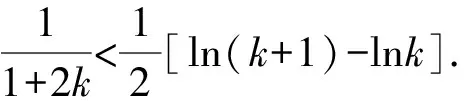

将上述式子相加可得:
原不等式得证.
评析对考生而言,完成以上这样的对接赋值具有极高的难度,需要较强的数学抽象能力和直观想象能力,他们往往束手无策,望题兴叹而已!
4 难点突破策略

由此可运用化整为零策略,令
当n≥2时,则
bn=Sn-Sn-1
由此只需证明


求导或利用第(2)问的结论便可轻松予以证明.
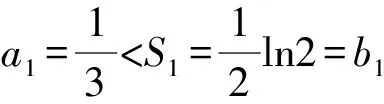
故对任意n∈N*,an 将函数、导数、数列、不等式结合的综合问题是近年来高考的热门题型.解题者遵循“求和看通项”这种化整为零的思路破解这类试题,而命题者则遵循“从通项生成和”这种逆向思维命制试题,命题过程中充分体现了函数与方程、化归与转化、化整为零的数学思想,本种命题手法在全国高考卷中屡见不鲜. 例2 (2017年全国Ⅲ卷理科22)已知函数f(x)=x-1-alnx. (1)若f(x)≥0,求a的值; 进而不等式两边分别构造两个数列,其中右边转化成常规的等比数列求和,问题便水到渠成. 例3 (2014年高考全国Ⅱ卷理科17题)已知{an}满足a1=1,an+1=3an+1. 为什么有许多学生解决不了一些并不复杂甚至是简单的数学问题呢?除了极少数学生不知道相应的数学知识外,绝大部分学生不是不会方法,而是由于没有站在思想的高度来思考和引领方法,或者是因为思想不明确而想不起来用什么方法来处理问题. 上述试题的自然解法源于数学思想的指引,善于观察不等式的结构特征,把不等式两边看成两个数列的求和,从而构造两个数列,把研究和的大小转化成判断通项的大小,体现了化整为零、化归与转化、函数与方程思想在数学解题中的重要作用. 解题是命题的基础,命题是解题的超越.作为一线数学老师,不但要研究试题的解题方法、分析试题的产生背景,还要揣摩命题者的思路、懂得试题的命制原理,这样才能促使自己在教学中能更好地引领学生把握试题的本质,从数学思想方法的高度提高解题的能力和素养.5 命题路径探秘
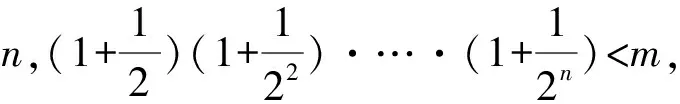

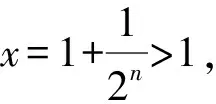
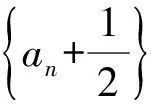
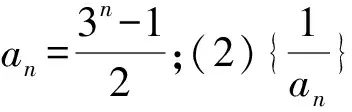
6 教学研究感悟

