高中数学数列试题的解题方法与技巧
姬秀云
(山东省东营市第一中学 257000)
在整个高中数学教材中,数列和函数导数的解题方法最多,也最能体现多样的数学思维.数列章节作为高考高频考点和数学多样思维的体现,在求通项及求前n项方面有着众多的方法,需要教师进行细致地分类和讲解,并列举典型的例题让学生进行更好地吸收.
1 高中数学中数列知识的内容和重要性
1.1 数列章节的基本知识和教学内容
数列在各地的高考中都占据着十分重要的地位,往往分值较高难度较大,是教学工作中的重难点.在这一章节中,书本主要讲述了等差数列、等比数列以及两个数列的综合应用.虽然大纲上轻描淡写,但其中包含的数学思想和数学方法却十分丰富,尤其是在求数列通项和数列求和两方面,方法五花八门且应用灵活.教师需要将各类方法进行细致归类,并选取典型例题对学生进行详细讲述,让学生依据例题进行举一反三,实现数学思维和能力的升格.
1.2数列章节对整个数学学习过程的重要意义
数列这一章节所用到的倒序相加、错位相减、累加法、累乘法等解题方法体现了各类数学思想的魅力.这些方法的思想内核不仅与函数、导数等章节息息相关,对学生日后进入大学学习高等数学中的极限和积分也有着十分重要的基础作用.在进行方法指导时,依据函数导数等知识与数列间的联系,充分打开学生的发散性思维,提高学生的数学学科素养,对有能力的学生也可进行适当的极限和积分方面的拓展延伸,便于学生形成更为全面和完整的思维体系.
2 求数列通项的解题方法与技巧
数列章节的知识主要分为等差数列、等比数列和等差等比数列的综合应用,在整个章节中,对各类方法的要求十分繁杂,尤其在求解通项公式和数列求和两个方面,有着众多的解法.求数列通项的方法主要包括定义法、累加和累乘法、构造当遇到等式右面是分式且较为复杂,同时与左面的倒数有关系时,可采用取倒数的方式进行新数列的构造.除此以外,对一些特殊的数列,可以通过简单的观察归纳法和复杂的对数求解等进行额外方法的处理,最后得出相应的通项公式.
2.1 定义求通项法
利用等差、等比数列的定义求通项、主要适用于给出Sn和an之间关系的试题,可利用an=Sn-Sn-1这个公式进行相关求解.求解时,需要额外考虑a1=S1这一特殊情况.
例如对Sn=2n2-3n进行数列通项求解时,可先考虑第一项,把n=1代入,可得出a1=S1=-1,随后利用上述公式,得出an=Sn-Sn-1,n≥2且n恒为正整数.这时可得出an=2n2-3n-2(n-1)2+3(n-1),化简求解后,若a1也符合这个式子,则直接得出an等于这个式子,否则需要将其与n≥2的情况分开.这类方法利用的条件在于题目中给定Sn与an的关系,或者题目中给出Sn的表达式.
2.2 累加和累乘方法
累加法适用的试题模板是an+1=an-f(n).针对这一式子,需要通过移项,把an移到等式的左面,然后依次给n从1到n赋值,等式两边分别进行上下相加,最后将两边都消解成一个式子.
例如an+1=an+2n,a1=2这个试题,在求解的过程中可以先移项,再依次将n赋值,首先是a2-a1=2,a3-a2=4,a4-a3=6,…,an+1-an=2n,然后将等式左面先相加,得出an+1-a1这个代数式,这时等式右面的和为2+4+6+…+2n,我们会发现这是一个等差数列,直接利用等差数列的求和公式进行求解,再加上给出的a1值便可得出an+1的通项公式,通过变形便可得出an.累乘法与累加法原理相同,只是将累加过程中的加减运算改变成了乘除运算.适用公式是an+1=an·f(n).
2.3 构造法
这类方法是待定系数法,通过构造相关函数等形式对复杂的式子进行变形.最为基础的形式为an=kan-1+t,可以利用待定系数法将式子变形成an+m=k[an-1+m],在保证式子与原式相等的基础上构造出新数列an+m,这个新数列是一个等比数列,前一项与后一项的比值为k.当把t换成f(n-1),则前面一项在构造时则相应变成f(n),即构造an+f(n)=k[an-1+f(n-1)].
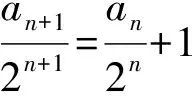
2.4 倒数法
这类方法主要适用于等式两边存在分式,而分子部分相对复杂,且分式左右两边存在着密切联系的情况.首先是等式左边通常是an或者其他的数列单独式子,等式右边的分子和左边类似,也是一个单独的式子.分母部分往往较为复杂.
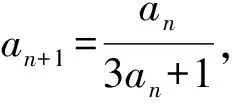
2.5 其他方法
除了以上的几种常用方法以外,求解数列的通项公式还有观察法、归纳法和直接利用公式等.对于一些较为简单的公式,可以通过下标和辅助公式进行初步处理,然后通过求数列通项公式进行直接求解.对一些特殊的数列,如斐波拉契数列等,往往会在试题中给出特殊数列的前几项,需要学生通过观察与分析得出数列的基本规律,然后进行相关的试题解答.有些数列本身十分复杂,需要学生通过取对数等手段进行处理,教师可对这些方法进行简单介绍,便于数学思维能力较强的学生攻克复杂的试题,获得更大的提升.
3 数列求和的方法和技巧
除了求数列的通项之外,数列求和也是高考中十分重要的考查内容,主要包括错位相减法以及裂项相消法,除此以外,还有分组求和法以及倒序相加法等.教师在进行教学时,可依据例题对学生进行介绍与举一反三,让学生灵活应用这些方法解决相关习题.
3.1 错位相减法
错位相减法主要用于解决等差比数列的求和问题,在原数列求和的基础上乘上等比数列的q值,然后上下两个式子进行相减,得到(1-q)Sn.
例如等差比数列cn=an·bn,{an}是等差数列,{bn}是等比数列,这时将两个式子进行相乘,便可采用错位相减法,首先计算Sn=a1×b1+a2×b2+…+an×bn,然后在下一行进行q×Sn的计算,把a1×b1的位置空掉,从第二个位置下面开始写:a1×b2+a2×b3+…+an×bn+1,然后将上下两个式子相减,得到(1-q)Sn=a1×b1+b2(a2-a1)+…-an×bn+1,然后可以在这一式子中得到新的等比数列,利用对应的求和公式进行求解即可.这类数列求和的方法主要应用在等差数列与等比数列相乘的情况下,尤其需要注意的是有的时候两个数列以相除的方式出现,这时可以看做等差数列与等比数列的倒数进行相乘,仍然可以采用错位相减的解题方法.
3.2 裂项相消法
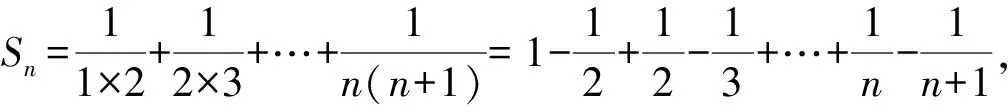
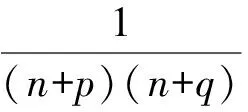
3.3 分组求和法
这类求和方法通常适用于不同数列的相加和相减过程,这时需要将两个式子进行分开求和,最为常见的是一个等差数列和一个等比数列之间进行相互加减运算.例如cn=2n+n,首先可利用等比数列的求和公式对整个式子的前面部分进行求和,再利用等差数列的求和公式对后面的式子进行求和,然后将这两次求出的和相加,便可得到最终的求和结果.在对带有绝对值的数列进行求和时,一定要注意对大于零和小于零的部分进行分组求和.
例如在对an=|2n-5|进行求和时,先要找出这个绝对值内部的式子大于零的拐点,也就是n=3,然后对n<3和n≥3两种情况进行展开讨论,前一种情况直接进行计算,而后一种情况则是利用前三项的和再加上剩余项的和来实现数列的最终求和过程得到结果.
在新课标改革的背景下,高中数学更加重视学生的实践应用能力和数学思维的培养.而数列这一章节对学生思维能力的训练和数学学科素养的塑造有着十分重要的意义.在数列这一章节的解题过程中,所应用到的方法五花八门,主要表现在数列的求通项过程和数列的求和过程,教师可通过典型的例题对各类方法进行分类总结,并通过举一反三的训练让学生充分掌握这些方法,在训练的过程中提高思维能力.数列求通项主要包括定义法、累加累乘、构造法、倒数法以及观察归纳和其他一些高难度的方法,而数列的求和过程主要包括等差比数列的错位相减、分式的裂项相消、多项式的分组求和法三种,教师应做好各类方法的分类整合工作.

