高中数学解题中向量法的运用

陈苏平

(江苏省南京市溧水区第二高级中学 211200)

运用向量法解答高中数学习题的难点在于如何根据已知条件构建合理的向量，因此教学中应注重给予学生运用向量法解题的引导，而后要求学生灵活运用向量的几何及其坐标运算知识顺利地求解相关习题，使学生亲身体会用向量法解题的简便之处.

1 向量法用于解答三角函数习题

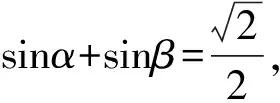
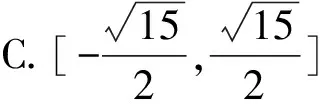
解析由题意可设m=(cosα，sinα)，n=(cosβ，sinβ)，则m+n=(cosα+cosβ，sinα+sinβ).

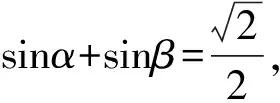
又因为0≤|m+n|≤|m|+|n|，

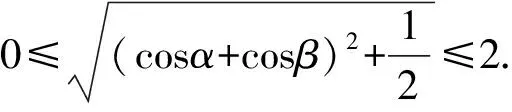
点评应用向量法解答三角函数习题时，既要注重利用三角函数的相关公式以及一些隐含条件，又要根据已知条件运用向量构建不等关系.

2 向量法用于解答不等式习题

点评运用向量法求解不等式习题具有一定的技巧性，可根据解题经验以及已知条件构建相关向量，而后运用向量与其模之间的关系进行求解.

3 向量法用于解答平面几何习题

解析建立如图1所示的平面直角坐标系：

图1

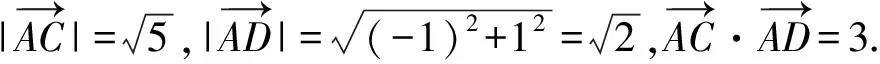
点评运用向量法求解几何问题时，通常构建平面直角坐标系，借助向量的坐标运算简化解题步骤，提高解题效率.

4 向量法用于解答立体几何习题

例4如图2，已知三棱柱ABC-A1B1C1中∠BAC为直角，AB=AC=1，BB1=2，∠ABB1=60°.若B1C=2，求二面角B1-CC1-A的余弦值.

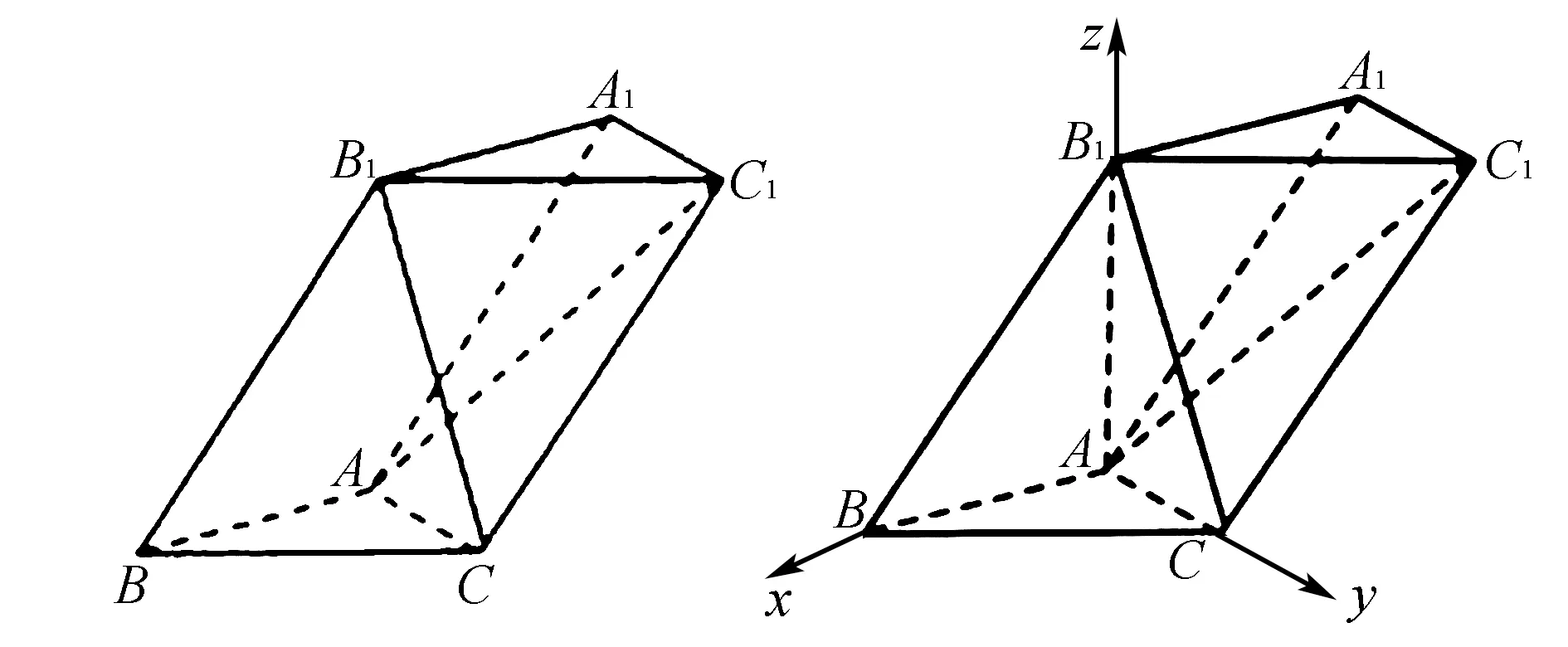
图2 图3

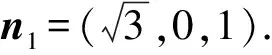
设n2=(x2，y2，z2)为平面B1CC1的法向量,

设二面角B1-CC1-A的平面角为θ，则

点评解题的关键在于构建正确的空间直角坐标系，找到线、面相关的向量以及法向量，而后通过数学运算求解.

5 向量法用于解答直线与圆习题

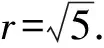
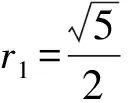
点评向量法与几何知识有着密切的联系，因此，解题时应注重熟练运用向量知识并借助数形结合的思想，更加直观地寻找相关点、线段之间的关系，达到化难为易，迅速解题的目的.

6 向量法用于解答数列习题

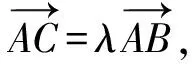
所以an-1+an+1=1-λ，1-an=λ.

所以an-1+an+1+1-an=1.

所以an-1+an+1=an，an+an+2=an+1，an-1+an+1+an+2=an+1.则an-1+an+2=0，an+an+3=0，an+3+an+6=0.所以an=an+6.

数列{an}是以6为周期的数列，因为a1=a2=1，所以a3=a2-a1=0，a4=a3-a2=-1，a5=a4-a3=-1，a6=a5-a4=0.

所以a1+a2+a3+a4+a5+a6=0.

因为2021=6×336+5，

所以S2021=S5=0.

点评向量常作为工具解答高中数学相关习题，尤其当遇到向量与数列相结合的习题时，应注重积极联系所学的向量结论迅速地找到解题切入点.

7 向量法用于解答圆锥曲线习题

解析由双曲线离心率定义可知，

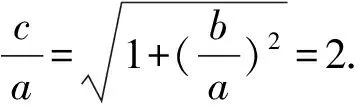
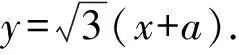
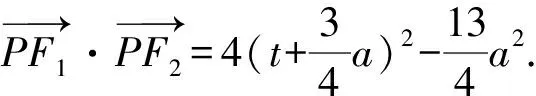
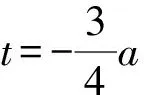
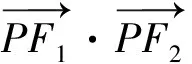
点评运用向量法解答圆锥曲线习题并注重灵活运用向量的相关运算，同时还应注重对要求解的结果进行适当地转化，运用换元法降低计算复杂度，确保问题得以顺利突破.