圆锥曲线中的直角弦问题

卢会玉

(甘肃省嘉峪关市第一中学 735100)

圆锥曲线中的直角弦问题是高考考查的一个重要考点，也是一类特征非常明显的问题.可以通过探索找到涉及直角弦问题的试题特点，找到解决问题的合适方式.

1 直角弦定义

直线与曲线相交于两点A,B，若存在点P，使得PA⊥PB，则弦AB叫做相对于点P的直角弦.

2 椭圆中的直角弦

2.1 椭圆与双曲线中相对于曲线中心的直角弦

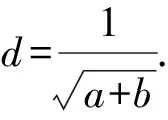
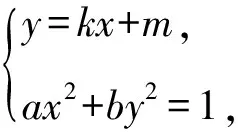
(a+bk2)x2+2kmbx+bm2-1=0.

设A(x1,y1),B(x2,y2)，由韦达定理,得

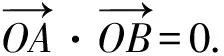
即x1x2+y1y2=0.

所以x1x2+y1y2=x1x2+(kx1+m)(kx2+m)

=(k2+1)x1x2+km(x1+x2)+m2=0.

则(a+b)m2=k2+1.

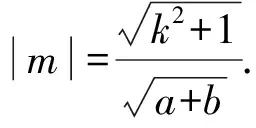
所以原点O到直线l的距离为

所以原点O到直线l的距离d为定值.

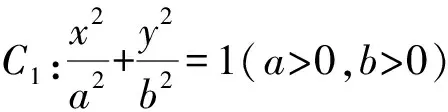
(1)求C1的方程;

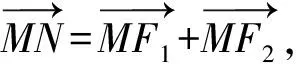
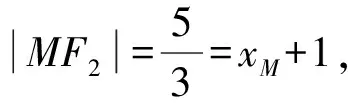
点M到(1,0),(-1,0)距离之和为2a=4.

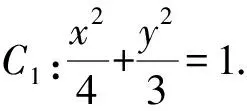
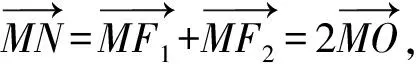
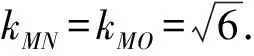
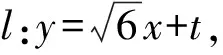
设A(x1,y1),B(x2,y2)，由韦达定理,得

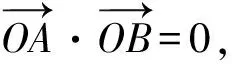
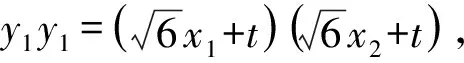
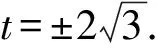
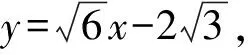
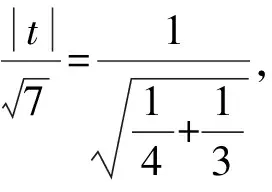
2.2 相对于椭圆上点的直角弦

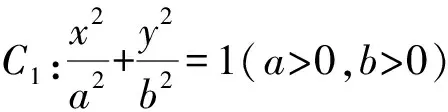
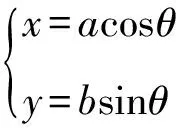
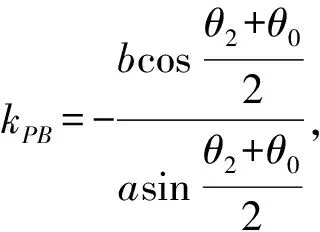
若PA,PB的斜率存在，则kPA·kPB=-1.

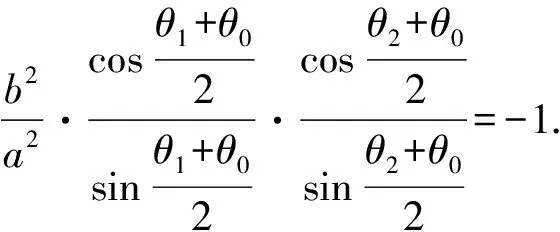
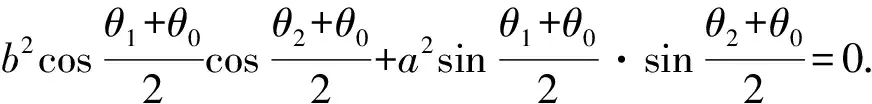
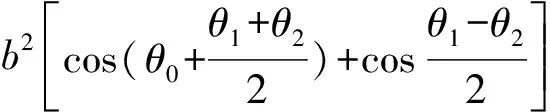
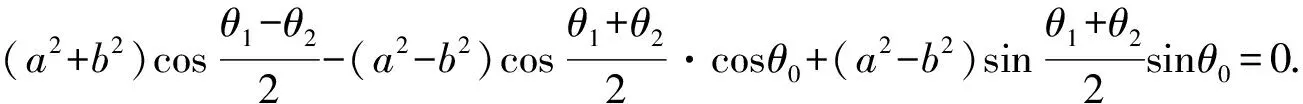
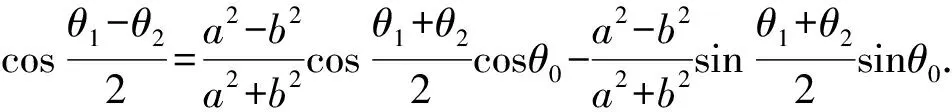
①

即为θ0,θ1,θ2之间满足的关系式.

又直线AB的方程可写为

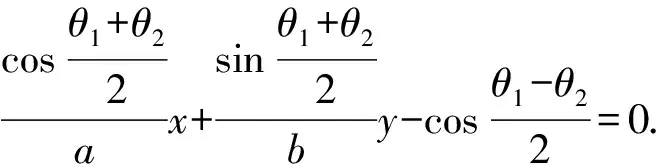
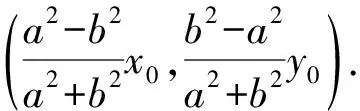
当PA或PB的斜率不存在时，不难证明上述结论也成立.

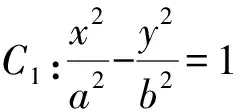
(1)求C1的方程；

(2)椭圆C2过点P且与C1有相同的焦点,直线l过C2的右焦点且与C2交于A,B两点,若以线段AB为直径的圆过点P,求l的方程.

解析(1)设P(x0,y0)，则切线方程为

x0x+y0y=4.

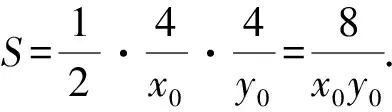
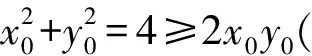
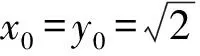
可得a2=1,b2=2.

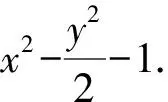
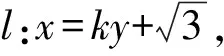
设A(x1,y1),B(x2,y2)，由韦达定理,得

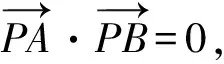
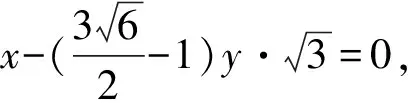
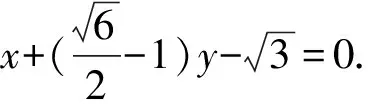
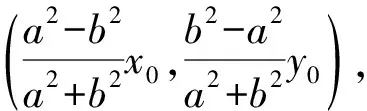
2.3 相对于非椭圆上点、非中心点的直角弦

(1)求椭圆C的标准方程；

(2)过点H(-2,0)的直线交椭圆C于A，B两点，若AF1⊥BF1，求直线AB的方程．

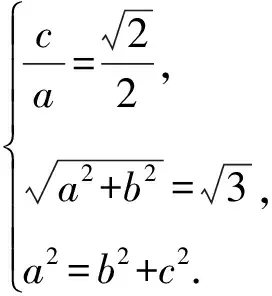
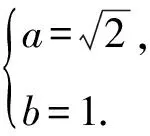
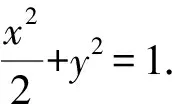
(2)由题知，点F1的坐标为(-1,0)，显然直线AB的斜率存在.

设直线AB的方程为y=k(x+2)(k≠0)，

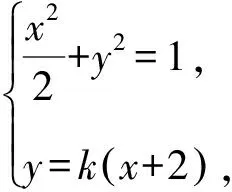
得(1+2k2)x2+8k2x+8k2-2=0.

则Δ=(8k2)2-4(1+2k2)(8k2-2)

=8(1-2k2)>0.

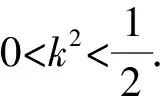
③

设A(x1,y1)，B(x2,y2)，则

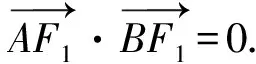
则(-1-x1,-y1)·(-1-x2,-y2)=0.

即1+x1+x2+x1x2+k(x1+2)·k(x2+2)=0.

整理,得

(1+2k2)(x1+x2)+(1+k2)x1x2+1+4k2=0.

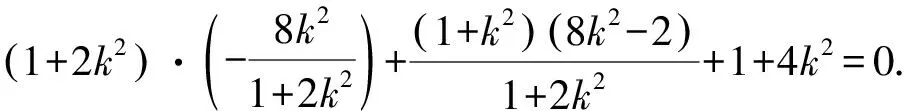
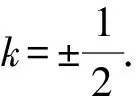
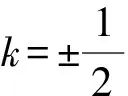
所以直线AB的方程为

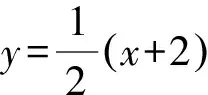
即直线AB的方程为

x-2y+2=0或x+2y+2=0．

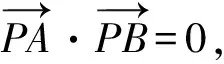
3 抛物线中的直角弦

结论3 抛物线相对于曲线中心的直角弦：直线l交y2=2px(p>0)于A(x1,y1),B(x2,y2)两点,O为原点，若OA⊥OB，则直线l恒过定点(2p,0).

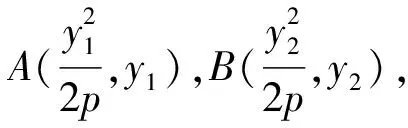
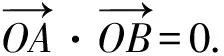
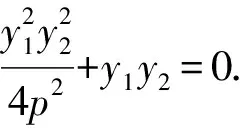
所以y1y2=-4p2.

设AB:x=my+n，代入抛物线y2=2px,

得y2=2p(my+n).

即y2-2pmy+2pn=0.

故y1y2=-2pn.

所以-2pn=-4p2.

即n=2p.

所以AB:x=my+2p.

可知弦AB恒过定点(2p,0).

结论4 直线l交y2=2px(p>0)于A(x1,y1),B(x2,y2)两点,O为原点，若OA⊥OB，且OM⊥AB,则点M的轨迹为x2+y2=2px(x≠0).

证明因为OA⊥OB，

则可知AB恒过定点(2p,0).

故可设AB所在直线的方程为y=k(x-2p).

又因为OM⊥AB,

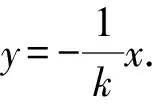
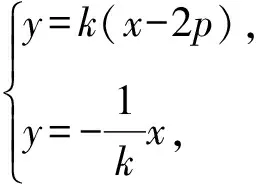
x2+y2=2px(x≠0).

结论5直线l交y2=2px(p>0)于A(x1,y1),B(x2,y2)两点,O为原点，若OA⊥OB，则ΔAOB面积的最小值为4p2.

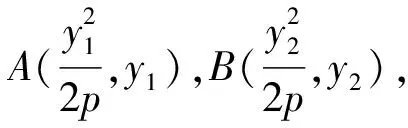
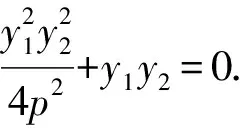
所以y1y2=-4p2.

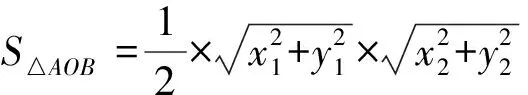
=4p2，

当且仅当y1=y2时等号成立.

结论6 直线l交y2=2px(p>0)于A(x1,y1),B(x2,y2)两点,O为原点，若OA⊥OB，则弦AB的中点N的轨迹方程为y2=p(x-2p).

证明因为OA⊥OB，

则可知AB恒过定点(2p,0).

故可设AB所在直线的方程为y=k(x-2p).

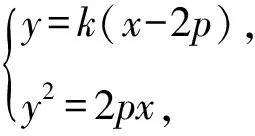
k2x2-(4k2p+2p)x+4k2p2=0.

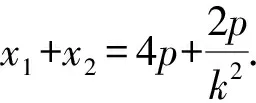
所以y1+y2=k(x1-2p)+k(x2-2p)

=k(x1+x2)-4kp

设弦AB的中点N(x0,y0)，则

消去k得中点N的轨迹方程为y2=p(x-2p).

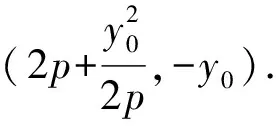
证明显然直线AB不与x轴垂直.

故可设其方程为x=my+n.

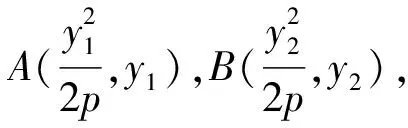
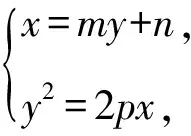
得y2-2pmy-2pn=0.

则y1+y2=2pm,y1y2=-2pn，

因为MA⊥MB，显然MA,MB的斜率存在.

所以kMA·kMB=-1.

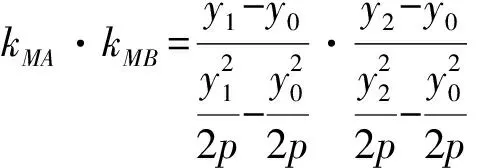
=-1.

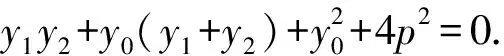
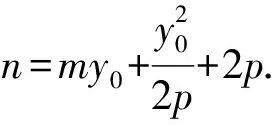
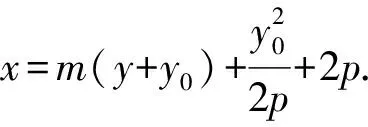
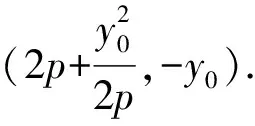
4 双曲线中的直角弦

相对于双曲线上点的直角弦

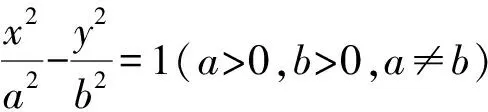
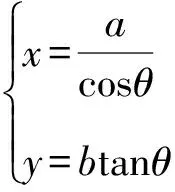
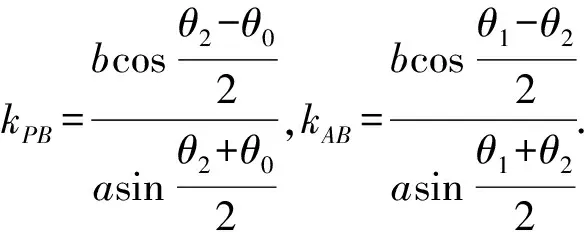
若PA,PB的斜率存在，则

kPA·kPB=-1.

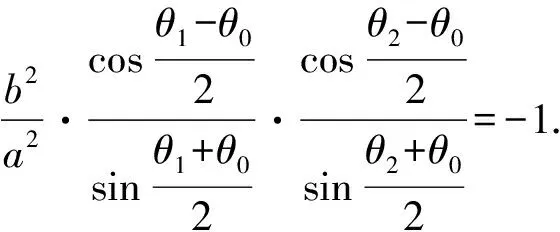
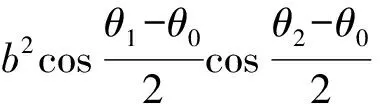
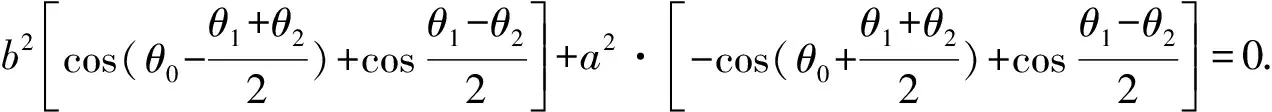
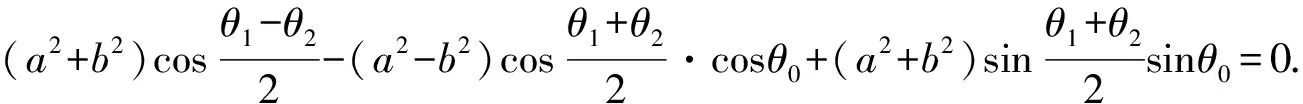
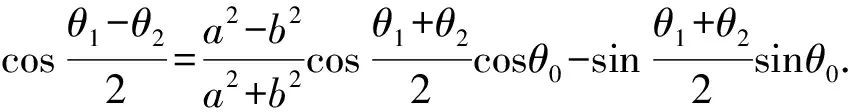
④

即为θ0,θ1,θ2之间满足的关系式.

又直线AB的方程可写为

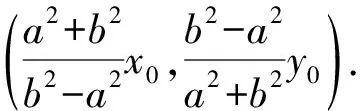
当PA或PB的斜率不存在时，不难证明上述结论也成立.