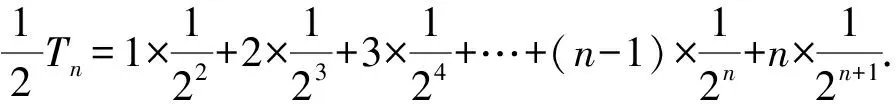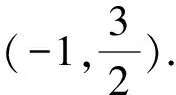高中数学数列试题的解题技巧

刘 鹏

(安徽省利辛县第一中学 236700)

数列是高中数学的重点、难点，习题情境复杂多变，部分习题技巧性较强.为提高解答数列试题的能力，既要总结常见的数列习题类型，又要注重深入研究经典例题，掌握题型特点，总结相关解题技巧.

1 数列试题解题技巧之公式法的应用

例1在数列{an}中，a1=2，an+1=an+2n+1，数列{bn}满足bn=2log2(an+1-n)，则数列{bn}的前n项和Sn为( ).

A.n2B.n2-nC.n2+nD.n2+n+1

解题技巧高中数学数列部分涉及很多公式，解题时直接套用公式可大大提高解题效率.解答该题需要从给出的已知条件出发通过构造新的数列求解出数列{an}，通过计算得出数列{bn}的通项公式，而后直接套用等差数列前n项和计算公式.

因为an+1=an+2n+1，

所以an+1-2n+1=an+2n+1-2n+1=an-2n+1.

所以(an+1-2n+1)-(an-2n)=1.

因为a1=2，所以a1-2=2-2=0.

则数列{an-2n}是以0为首项，1为公差的等差数列.所以an-2n=n-1，即an=n-1+2n.

因为bn=2log2(an+1-n)，

所以bn=2log2(n-1+2n+1-n)=2n.

2 数列试题解题技巧之数列分组法的应用

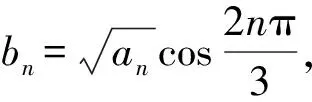
解题技巧解答数列与三角函数相结合的试题不仅要运用数列相关知识，而且需要运用相关的诱导公式.该题中需根据已知条件求出数列{an}的通项公式，得出数列{bn}的通项公式，结合三角函数，找到数列{bn}中不同项数的通项公式.

因为nan+1=(n+1)an+n(n+1)，

b3k=3kcos2kπ=3k；

因为2020=3×674-2，

又因为2020=3×673+1，

3 数列试题解题技巧之裂项相消法的应用

A.{0，1，2} B.{0，1，2，3} C.{2} D.{0，2}

解题技巧部分数列习题，需要运用递推关系研究相关项数之间的联系，对分析以及推理能力要求较高.该题中需根据已知条件寻找相关的递推关系，采用裂项相消法求出Sn.根据已知条件判断数列{an}的单调性，而后通过分类讨论进行解答.

因为an+1-1=an(an-1)，两边取倒数，得

又因为an+1-1=an(an-1)，

所以an+1-an=(an-1)2.

因为an≠1，所以(an-1)2>0，数列{an}为递增数列.

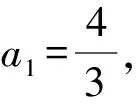
综上可知，Sn的整数部分可能构成的集合是{0，1，2}，故选A.

4 数列试题解题技巧之累加、累乘法的应用

例4对于数列{an}，若存在常数M，使得对任意的n∈N*，都有|an|

解题技巧解答数列新定义类问题的关键在于能够构建新定义与所学知识的联系，对要求解的问题进行灵活转化，化陌生为熟悉，尤其需要灵活运用多种解题方法进行严谨地推理.

对于A,C两项，设数列{an}有界，根据定义可知，an

而1+n→+∞，1+2n→+∞，因此，两项均错误.

因为a2-a1=0，所以a1=a2=1.

所以an<4成立.故选D.

5 数列解题技巧之错位相减法的应用

例5已知{an}是公差不为0的等差数列，已知a1=1，且a1,a2,a4成等比数列，数列{bn}的前n项和为Sn，b1=2，bn=Sn-1+2(n≥2，n∈N*)，设an=bncn.

(1)求数列{cn}的通项公式；

(2)记Tn为数列{cn}的前n项和，若对于任意的n∈N*，不等式bn·Tn>(-2)np-n恒成立，求实数p的取值范围；

解题技巧遇到数列求和时应注重先观察求和数列的通项公式，尤其当通项公式为等差数列与等比数列的复合形式时常采用错位相减法.该题中首先根据已知条件求出数列{an}，{bn}的通项公式，而后借助“an=bncn”求出数列{cn}的通项公式.求{cn}的前n项和Tn时需要运用错位相减法.

问题(1)因为{an}是公差不为0的等差数列，a1=1，且a1，a2，a4成等比数列.所以a22=a1a4.

设公差为d，则(1+d)2=1×(1+3d).

整理,得d(d-1)=0.则d=1，an=n.

因为当n≥2时，bn=Sn-1+2，则bn+1=Sn+2.两式相减,得bn+1-bn=Sn-Sn-1=bn.

所以bn+1=2bn.

当n=2时，b2=S1+2=b1+2=4，故b2=2b1.

所以数列{bn}是以2为首项，以2为公比的等比数列.所以bn=2×2n-1=2n.

①

②

因为不等式bn·Tn>(-2)np-n恒成立，