基于神经网络PID控制器的压铸机压射速度控制系统的设计

杨力，徐林森

应用技术

基于神经网络PID控制器的压铸机压射速度控制系统的设计

杨力1，徐林森2

（1. 常州工业职业技术学院，江苏 常州 213164；2. 中国科学院合肥物质科学研究所，合肥 230031）

通过神经网络PID控制器，提高铸件过程中对压铸机压射速度的准确控制，以改善铸件的品质。首先，从压射系统的结构出发，分析其工作过程，通过输入电压求取电液伺服装置的传递函数，利用比例阀所受压力，计算其端口流量，进而完成压射系统的建模。然后，以STM32F103RE处理器为核心，配以输入电路、反馈电路等外围单元，设计压射速度控制系统的硬件框架。以PID算法为基础，将压射速度的误差引入到神经网络算法中，对PID算法的参数进行整定，以形成能够自适应调整参数的神经网络PID算法，进而作为压射速度控制系统的控制算法，从而完成压射速度控制系统的设计，以实现对压射速度进行控制。通过对比实验表明，该方法在跟踪阶跃目标压射速度以及变化目标压射速度时，都能较为稳定、快速地跟踪压射目标速度的变化。该方法不仅对压射速度的控制准确度较高，而且控制过程较为稳定，对压射速度具有较好的控制性能。

压射速度控制；压铸机；STM32F103RE处理器；PID算法；神经网络PID控制器

随着人们生活品质的提升，对零部件的需求也在不断提高。在零部件的生产过程中，压铸机扮演了重要角色[1-2]。零部件的铸件过程可通过压铸机完成，但要想获得高品质的铸件，压铸机的压射速度控制至关重要，只有准确控制压射速度，才有利于提高铸件质量和效率[3-4]。

近年来，智能化控制技术不断发展，人们也对压射速度的智能化控制展开了研究。张叶茂等[5]采用MKE06Z128VLK4处理器作为核心器件，配以压力采集电路，设计了智能压射速度控制系统，在该系统中采用模糊PID算法作为控制策略，来实现对压射速度的控制。该系统的控制过程较为稳定，但控制准确度不够高。吴星等[6]采用EP9315处理器联合快压射开关检测方法，设计了压射速度控制系统的控制电路，配以模糊PID算法，对压射速度进行控制。该方法能够自适应地调整PID参数，但控制准确度有待提高。张叶茂等[7]在对压射系统进行数学建模后，在模糊PID算法的基础上，引入变论域理论，设计了压射速度的控制算法。该方法控制准确度有所提高，但计算过程较为复杂，使控制过程的稳定性有待改善。

文中在对压射系统的结构进行分析后，对其进行了建模，接着根据压射系统的工作过程，设计了压射速度控制系统的框架。利用STM32F103RE处理器，搭载触摸显示屏等外围电路，构建了压射速度控制系统的硬件模块。利用神经网络方法对PID算法的参数进行自适应整定，建立了神经网络PID算法，配合硬件控制电路，对压射速度进行控制。采用对比实验的方法，对文中方法的压射速度控制性能进行了验证。

1 压射系统的建模

在铸件过程中，压射速度的控制至关重要。压铸机的压射系统主要由增压储能器、电液伺服装置、压射缸等部分组成。压射系统的结构如图1所示[8-9]。

在图1中，T为增压储能器，D为增压缸，J为压射缸，M为负载，A为电液伺服装置，t为负载的速度，t为负载的弹性刚度，t为负载的阻尼系数，i、i、i（=1, 2）分别为增压缸和压射缸缸体的面积、压力和体积。在铸件时，压射系统要进行慢速、快速压射以及增压保压3个步骤，其中慢速和快速压射过程中，对压射系统的速度控制要求较高。在慢速压射时，需要以较慢的速度控制推杆，推动负载前进至浇注口。在快速压射时，需要以最快速度控制推杆前进，以实现快速充型。

图1 压射系统的结构

在压射过程中，压射速度是通过电液伺服装置的输出开度来控制的。电液伺服装置的传递函数()可通过其输入电压来表示，其表达式如下[10-11]：

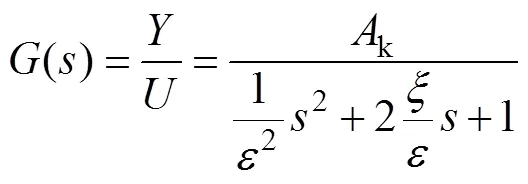
式中：k为流量增益；和分别为电液伺服装置中活塞的固有频率和阻尼比；为拉氏因子。

电液伺服装置中比例阀的端口流量，可通过其所受压力0及其端口开度0来计算，其过程如下：

式中：0为比例阀端口的初始流量。

压射过程中，在压射缸缸体中压力2的推动下，压射缸中推杆带着负载以速度t动作。此时t和2的关系式为：

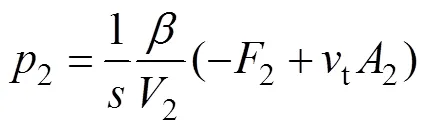
式中：为液压油弹性模量；2为压射缸的中推动推杆运动的流量。

考虑压射缸质量，联合式（1—3），可得出压射系统的开环传递函数G()为：

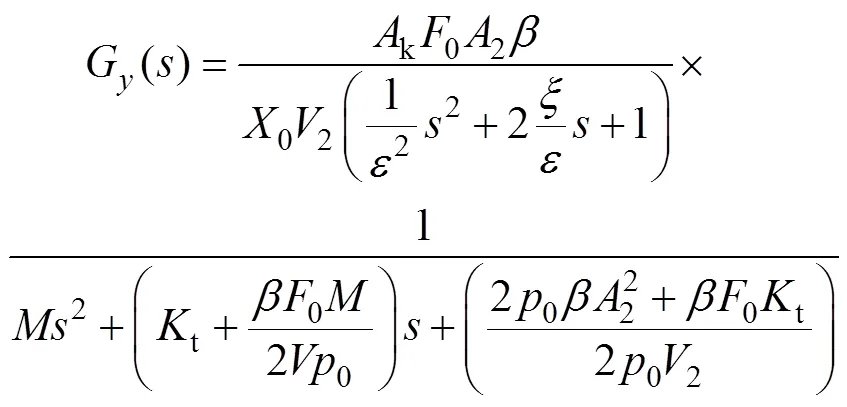
2 压射速度控制系统的框架设计

通过压射系统的建模可知，压射速度是通过电液伺服装置的输出开度来控制的，而电液伺服装置的输出开度又由比例阀来控制。因此，在压射控制系统的硬件电路中，通过对比例阀进行控制，产生压力，对压射缸内推杆的速度进行调节，从而完成对压射速度的控制。由此，文中设计了压射控制系统框架如图2所示。

图2 压射控制系统的框架示意

从图2可见，文中设计的压射控制系统，在采集到用户的控制要求及推杆的反馈压射速度后，将该信息送入中央处理器。中央处理器联合控制算法，得出控制信号，对比例阀的开度进行控制，进而调节压射缸中的压力，对推杆的速度进行调节，以实现压铸机压射速度的控制。

3 压射控制系统的硬件设计

从图2可知，在压射控制系统的硬件设计时，需要针对用户控制要求，考虑输入电路单元，反馈采集压射速度时的反馈电路单元以及中央处理器为中心的中心电路单元等。由此，文中设计了如图3所示的压射控制系统的硬件框图。

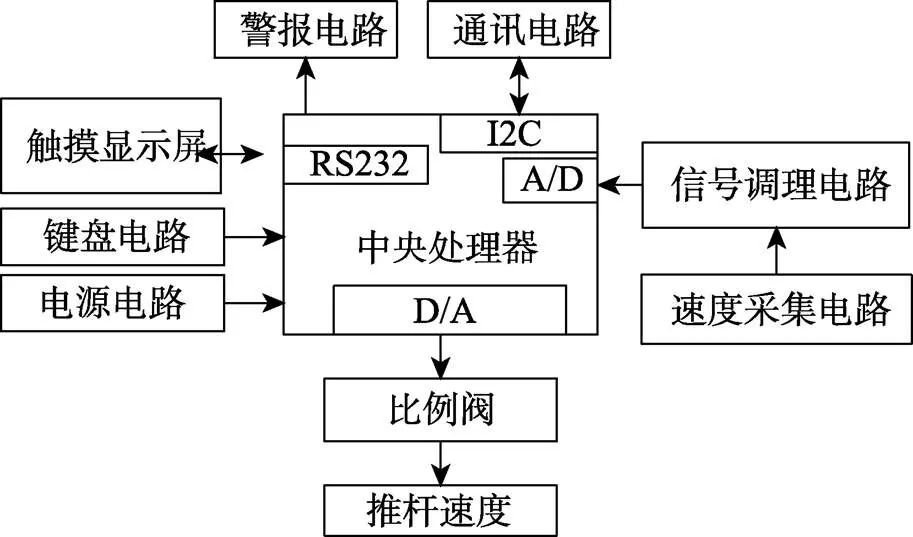
图3 压射控制系统的硬件框图

在图3中，触摸显示屏和键盘电路组成了供用户控制要求输入的输入电路单元，速度采集电路和信号调理电路组成了反馈压射速度采集的反馈电路单元，电源电路和中央处理器构成了中心电路单元。除此之外，图3所示的硬件框架中，还包含了警报电路和通讯电路，其中警报电路用于出现紧急情况时发出警报，通讯电路为硬件上的拓展接口，可用于系统的远程控制。

在图3中，触摸显示屏采用的是eView公司的ET070型7寸屏。该触摸屏支持RS232通信，具有800×480（像素）的分辨率和4线精密电阻网络，能适应于压铸机的工作环境。键盘电路采用的是3×3的九键电路。警报电路由喇叭和发光二极管组成，用于产生声光报警。通讯电路主要由SIMCOM公司的SIM7070G型无线通讯模块组成，该无线通讯模块支持I2C及RS232等多种通讯方式，具有功耗低、安全性能强等特点，可用于对压射控制系统的远程控制。速度采集电路采用Trans-Tek公司的LVT100型位移传感器来采集推杆速度的变化情况，并将该速度信号进行调理后送入中央处理器。中央处理器采用的是STM32F103RE处理器，其内部自带RS232、I2C等多种通信接口，以及A/D和D/A功能，能够便于其与触摸显示屏等外部设备通信，同时也能够便于其对模拟和数字信号转换的处理。同时STM32F103RE处理器的计算速度及稳定性都较强，能够较好地适应于压射速度控制过程的运算及信号处理需求。

在压射过程开始前，用户可借助触摸显示屏将控制需求通过RS232接口送入STM32F103RE中，同时也可通过触摸显示屏查看压射速度的控制情况。同时，LVT100型速度传感器可将采集到推杆速度的变化量经过调理后，送入STM32F103RE中的A/D转换器中，以将速度变化的模拟量转换成数字量。STM32F103RE再根据用户的控制需求和采集到的反馈速度，通过控制算法求取输出信息，该输出信号在送入比例阀之前，需要利用STM32F103RE中的D/A转换器将其转换成模拟信号，以控制比例阀的开度，进而完成对推杆速度的控制，实现压射速度的调节。在压射过程中，若出现紧急情况，用户可借助键盘电路控制系统急停、暂停以及开始等动作。当系统出现急停现象时，可通过警报电路，发出声光报警。另外，用户除了可通过触摸显示屏输入控制需求和查看压射速度的控制情况外，还可通过远程终端，经过SIM7070G无线通讯模块，与STM32F103RE进行数据交互，实现将控制需求送入STM32F103RE中，及时查看压射速度控制情况。

4 压射控制系统的控制算法设计

PID算法常被用于压射速度的控制过程中，虽然该算法较为简单实用，但是其参数欠缺自适应性能，易使控制准确度下降。对此，文中将引入自适应性能较好的神经网络算法，以对PID算法的参数进行整定，以提高系统的控制准确度。

PID算法是以时刻压射速度的误差()为基础来计算控制量()的。当时刻的反馈速度为()，目标速度为()时，()的表达式为[12]：

求取()后，对其进行比例、微分和积分计算，便可得出控制量()的表达式为：

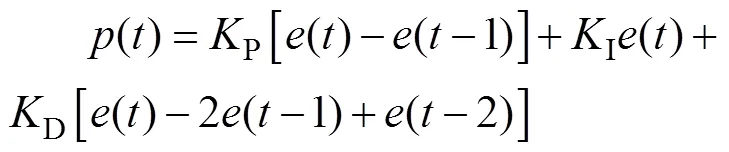
式中：P，I，D分别为比例、积分和微分参数。

由于式（6）中P，I，D不具备自适应性，在对其取值时，需要依靠经验不断对其进行调试，来获取适宜的P，I，D取值，从而导致系统的适应能力较弱，以及易导致系统的控制准确度降低。

神经网络算法可通过学习的方法，根据系统的误差，自适应地对P，I，D取值进行调整。对此，文中将利用神经网络算法对P，I，D进行整定，以形成神经网络PID控制器，对压射速度进行准确控制。

神经网络算法是在图4所示的3层网络结构上实现的[13-14]。

图4 神经网络结构框图

在图4中，k和k以及k（=1, 2, L, k）分别为神经网络的输入量、基矢量和权矢量。输出量的表达式为：

在神经网络的作用下，根据压射速度误差()，可得出P，I，D的整定过程为：

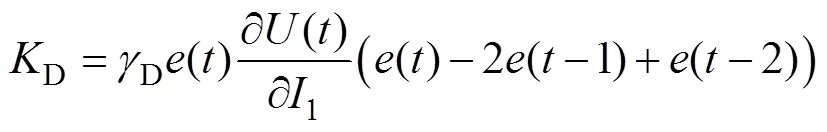
式中：γ(=,,)为学习效率。通过式（8—10）即可实现对PID算法参数的自适应整定。将式（8—10）和式（6）相联合，便构成了神经网络PID控制器。

5 实验结果

借助Matlab/Simulink软件搭建实验环境，对文中所设计的压射速度控制系统的有效性进行验证。同时与基于逆系统方法的压铸机快压射速度控制方法作对比，以便更为直观地观察文中方法的优越性能[15]。

5.1 阶跃速度控制测试

利用PID控制方法和基于逆系统控制方法，对阶跃目标速度进行跟踪测试，以观察2种方法对阶跃目标速度的跟踪准确性。以上2种方法对阶跃目标速度的跟踪结果如图5所示。

图5 PID控制方法和基于逆系统控制方法对阶跃目标速度的跟踪结果

从图5可见，PID控制方法和基于逆系统控制方法对阶跃目标速度跟踪时，在0.2 s附近二者较阶跃目标速度都发生了一定程度的偏差，但通过对比可见，文中方法的偏差更小。在0.21 s附近，PID控制方法和基于逆系统控制方法的跟踪速度都到达了阶跃目标速度处，但PID控制方法和基于逆系统控制方法的跟踪速度曲线，较阶跃目标速度曲线都发生了一次较大的偏差，观察2种方法的偏差量可以发现，文中方法跟踪速度曲线的偏差量为4.5 m/s，而基于逆系统控制方法跟踪速度曲线的偏差量为6.25 m/s。2种方法的跟踪速度曲线在产生此次较大偏差量后都进行了调整，在调整过程中，较阶跃目标速度而言，基于逆系统控制方法的跟踪速度曲线还出现了4次较大幅度的偏差，而文中方法仅出现了2次小幅的偏差。经过调整后，文中方法的跟踪速度曲线在0.26 s附近基本重合于阶跃目标速度曲线，基于逆系统控制方法的跟踪速度曲线在0.32 s附近才基本趋于阶跃目标速度曲线。在0.32～0.6 s期间，文中方法的跟踪速度曲线一直重合于阶跃目标速度曲线，基于逆系统控制方法的跟踪速度曲线还出现了多次偏离阶跃目标速度曲线的情况。由此可见，在对阶跃目标速度跟踪时，神经网络PID控制方法比基于逆系统控制方法的跟踪准确度更高，且偏离次数更少，能更好地适应对阶跃目标速度的跟踪，具有更为灵敏的阶跃响应。

5.2 变化速度控制测试

为了进一步观察文中方法的控制性能，PID控制方法和基于逆系统控制方法对具有多次变化的目标速度进行跟踪，通过观察2种方法跟踪速度曲线的变化情况，来判断2种方法的控制性能。PID控制方法和基于逆系统控制方法对变化目标速度的跟踪结果如图6所示。

图6 PID控制方法和基于逆系统控制方法对变化目标速度的跟踪结果

通过对比图6所示的PID控制方法和基于逆系统控制方法对变化目标速度的跟踪结果，可以发现较变化目标速度曲线而言，文中方法的跟踪速度曲线比基于逆系统控制方法的跟踪速度曲线更为贴合变化目标速度曲线，而且整个控制过程中，文中方法的跟踪速度曲线，较基于逆系统控制方法的跟踪速度曲线更为平稳。具体表现为，在0.1～0.3 s期间，文中方法的跟踪速度曲线产生了4次明显偏离变化目标速度曲线的情况，而文献[15]所提方法的跟踪速度曲线产生了7次明显偏离变化目标速度曲线的情况。且在0.1～0.3 s期间，基于逆系统控制方法的跟踪速度曲线比文中方法的跟踪速度曲线波动更为频繁，说明在此期间，文中方法控制的跟踪速度更为平稳。在0.3～ 0.4 s期间，文中方法的跟踪速度曲线产生了4次明显偏离变化目标速度曲线的情况，而基于逆系统控制方法的跟踪速度曲线产生了5次明显偏离变化目标速度曲线的情况。在0.35 s附近，PID控制方法和基于逆系统控制方法的跟踪速度曲线都出现了整个跟踪过程中较变化目标速度曲线的最大偏差。其中，文中方法跟踪速度曲线的最大偏差为5.21 m/s，基于逆系统控制方法的跟踪速度曲线的最大偏差为9.83 m/s。在0.4～0.6 s期间，文中方法的跟踪速度曲线产生了2次明显偏离变化目标速度曲线的情况，而基于逆系统控制方法的跟踪速度曲线产生了4次明显偏离变化目标速度曲线的情况。且在0.4～0.6 s期间，基于逆系统控制方法的跟踪速度曲线较文中方法的跟踪速度曲线产生波动的次数更多。由此可见，在对变化目标速度跟踪时，神经网络PID控制方法比基于逆系统控制方法具有更高的跟踪准确度，且跟踪过程更为平稳。说明文中方法对压射目标速度的变化更为敏感，能更灵活、快速地跟踪压射目标速度的变化，对压射速度的控制更为准确和稳定，具有较好的压射速度控制性能。

6 结语

对压射系统的结构进行了分析，并在此基础上对压射系统进行了建模，得出了压射系统的开环传递函数。根据压射系统的结构特点，采用STM32F103RE处理器设计了压射速度控制系统的硬件架构，并对硬件架构中各电路部分进行了选型。在PID算法的基础上，联合神经网络算法，利用压射速度的误差，对PID算法中的参数进行自适应整定，形成了神经网络PID算法，用以根据压射速度控制系统中的用户需求及反馈速度，求取输出信号，以实现对压射速度的控制。实验结果显示，文中方法对阶跃和变化目标速度的跟踪效果较好，能用于对压射速度进行准确的控制。

[1] AMOL R J, DEEPAK P H, PRAVIN P H. Design and Optimization of Gating System, Modification of Cooling System Position and Flow Simulation for Cold Chamber High Pressure Die Casting Machine[J]. Elsevier, 2021, 46(17): 7175-7181.

[2] PRIN B. Low-Pressure Die Casting Machine Selection Using a Combined AHP and TOPSIS Method[J]. Naresuan University Engineering Journal, 2020, 15(2): 1-11.

[3] 郑桂云. 12 000 kN挤压机双缸同步压射系统开发[J]. 特种铸造及有色合金, 2019, 39(6): 622-623.

ZHENG Gui-yun. Development of Double Cylinder Synchronous Injection System for 12 000 kN Squeezing Machine[J]. Special Casting & Nonferrous Alloys, 2019, 39(6): 622-623.

[4] ZAMORA R, FAURA F, LÓPEZ J, et al. Experimental Verification of Numerical Predictions for the Optimum Plunger Speed in the Slow Phase of a High-Pressure Die Casting Machine[J]. The International Journal of Advanced Manufacturing Technology, 2007, 33(3/4): 266-276.

[5] 张叶茂, 杨起兴. 基于嵌入式的压铸机控制系统设计[J]. 铸造技术, 2017, 38(3): 715-718.

ZHANG Ye-mao, YANG Qi-xing. Design of Control System of Die-Casting Machine Based on Embedded[J]. Foundry Technology, 2017, 38(3): 715-718.

[6] 吴星, 任文强. 基于模糊PID控制的压铸机自动控制系统设计[J]. 广西民族大学学报: 自然科学版, 2019, 25(4): 70-74.

WU Xing, REN Wen-qiang. Design of Die Casting Machine Control System Base on Fuzzy PID[J]. Journal of Guangxi University for Nationalities: Natural Science Edition, 2019, 25(4): 70-74.

[7] 张叶茂, 苏茜. 基于变论域自适应模糊PID的压铸机压射速度控制研究[J]. 热加工工艺, 2020, 49(1): 68-72.

ZHANG Ye-mao, SU Qian. Research on Die Casting Machine Injection Velocity Control Based on Variable Universe Adaptive Fuzzy PID[J]. Hot Working Technology, 2020, 49(1): 68-72.

[8] XI Z G, KE Y Q. Equal Accelerating Control of the Injection Speed of the Cold Chamber Die-Casting Machine[J]. Foundry Technology, 2006, 27(6): 562-564.

[9] 吴晓鸣, 王旭永. 压铸机速度控制系统的建模与仿真分析[J]. 江苏科技信息, 2019, 36(23): 49-51.

WU Xiao-ming, WANG Xu-yong. Modeling and Simulation Analysis of Speed Control System of Die Casting Machine[J]. Jiangsu Science & Technology Information, 2019, 36(23): 49-51.

[10] FENG Li-jun, YAN Hao. Nonlinear Adaptive Robust Control of the Electro-Hydraulic Servo System[J]. Applied Sciences, 2020, 13(10): 1-16.

[11] 闫孝姮, 陈伟华, 彭继慎. 基于CADE算法的压铸机实时控制压射系统的研究[J]. 特种铸造及有色合金, 2013, 33(7): 642-645.

YAN Xiao-heng, CHEN Wei-hua, PENG Ji-shen. Nonlinear Predictive Control for Rear Time Control Injection System of Die Casting Machine Based on CADE Algorithm[J]. Special Casting & Nonferrous Alloys, 2013, 33(7): 642-645.

[12] BRILLIANTO A C H, MAGHFIROH H, LAKSITA A T. Design Close-Loop Control of BLDC Motor Speed Using PID Method in Solar Power with Matlab/Simul­ink[J]. AIP Conference Proceedings, 2020, 2217(1): 1-7.

[13] 陈德平, 陈营, 罗建设. 基于BP神经网络风力发电机轴承座的铸造工艺参数预测模型[J]. 铸造技术, 2019, 40(10): 1086-1089.

CHEN De-ping, CHEN Ying, LUO Jian-she. Casing Process Parameter Prediction Model of Wind Turbine Bearing Pedestal Based on BP Neural Network[J]. Foundry Technology, 2019, 40(10): 1086-1089.

[14] BAU D, ZHU Jun-yan, STROBELT H, et al. Understanding the Role of Individual Units in a Deep Neural Network[J]. PNAS, 2020, 117(48): 30071-30078.

[15] 赵树忠, 朱红娜. 基于逆系统方法的压铸机快压射速度控制[J]. 机床与液压, 2019, 47(14): 144-146.

ZHAO Shu-zhong, ZHU Hong-na. Speed Control of Rapid Injection in Die-Casting Machine Based on Inverse System Method[J]. Machine Tool & Hydraulics, 2019, 47(14): 144-146.

Design of Injection Speed Control System of Die Casting Machine Based on Neural Network PID Controller

YANG Li1, XU Lin-sen2

(1. Changzhou Vocational and Technical College of Industry, Changzhou 213164, China; 2. Hefei Institute of Physical Science, Chinese Academy of Sciences, Hefei 230031, China)

The work aims to accurately control the injection speed of die casting machine in the casting process through neutral network PID controller, so as to improve the quality of castings. Firstly, from the structure of the injection system, the working process was analyzed, the transfer function of the electro-hydraulic servo device was obtained through the input voltage, the port flow was calculated by the pressure of the proportional valve, and then the modeling of the injection system was completed. Then, with STM32F103RE processor as the core and peripheral units such as input circuit and feedback circuit, the hardware framework of injection speed control system was designed. Based on the PID algorithm, the error of the injection speed was introduced into the neural network algorithm, and the parameters of the PID algorithm were adjusted to form a neural network PID algorithm that could adaptively adjust the parameters as the control algorithm of the injection speed control system, so as to complete the design of the injection speed control system to control the injection speed. According to the comparative experiments, this method could track the change of the injection speed of the step target stably and quickly when tracking the injection speed of the step target and changing the injection speed of the target. This method not only has high control accuracy for the injection speed, but also has stable control process and good control performance for the injection speed.

injection speed control; die casting machine; STM32F103RE processor; PID algorithm; neural network PID controller

10.3969/j.issn.1674-6457.2022.03.019

TP273

A

1674-6457(2022)03-0148-06

2021-12-05

国家重点研发计划（2017YFB1303202）；江苏省高校优秀科技创新团队项目（2019-48）；常州轻院校青年基金计划（QN201813101017）

杨力（1981—），男，硕士，讲师，主要研究方向为机械设计制造、材料加工技术。