整体壁板压展模具型面曲率半径的计算

韩金全，王少华，刘惠

整体壁板压展模具型面曲率半径的计算

韩金全1，王少华2，刘惠2

（1. 北京航空航天大学 机械工程及自动化学院，北京 100191；2. 中国航发北京航空材料研究院，北京 100095）

研究带有初始曲率的整体壁板在压展过程中的变形回弹规律，以确定压展模具的型面曲率半径。针对壁板压展回弹过程，用初始、加载和卸载3个典型状态来描述材料在截面圆周方向上的变形情况，推导应变和应力分布规律以及卸载后的力学平衡条件，从而得到壁板初始曲率半径、加载曲率半径以及卸载回弹后曲率半径之间的关系。再利用有限元仿真和试验，对理论推导的结果进行验证。通过数值计算，对比了理论计算中采用不同材料模型所得到的结果，表明材料模型的准确性对计算结果有较大的影响。得到了给定回弹后曲率半径情况下初始曲率半径与加载曲率半径之间的数值关系，以及给定初始曲率半径情况下加载曲率半径与回弹后曲率半径之间的数值关系，有限元仿真和试验结果验证了后者的准确性。通过对整体壁板压展过程进行理论推导，得到的结果能够较准确地描述曲率半径的变化规律，可作为压展模具型面设计的依据。

整体壁板；压展；回弹；应变分布

整体带筋壁板的制造，一般可以采用厚板整体铣削的加工方式，或者通过腹板焊接筋条的方法获得。整体铣削方式，其优点是结构完整性良好，但加工过程耗时过长，尤其批量生产时，加工效率较低，同时材料浪费严重，而且，壁板尺寸受到加工设备的限制，长度不能过大。焊接方式可以在很大程度上提高加工效率和材料利用率，且结构尺寸不受限制，但其结构强度和精度相对较差。为解决上述2种方式的弊端，可采用整体挤压方式，结合压展、校形等工艺，来加工整体带筋壁板。这种方法具体来说，就是采用型材挤压的加工方法制造带筋圆筒，如图1a所示，再将圆筒在某一特定周向位置，沿轴向剖切开，然后压展和校平，得到最终的整体带筋壁板，如图1b所示。在此过程中，壁板压展是重要的一个步骤。

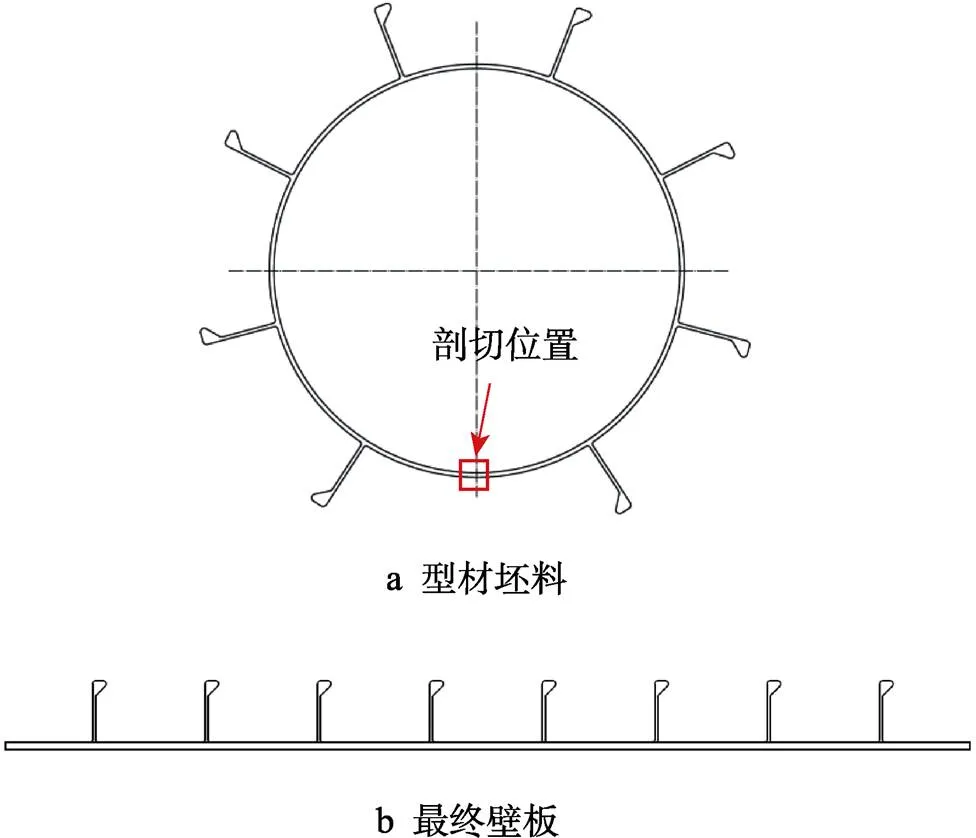
图1 壁板示意

压弯是整体壁板成形的常见方式之一，通常是在平面形状的壁板上压制出一定的曲率[1-2]，同样，也可将带有一定初始曲率的壁板展平。展平模具的型面如图2所示，下模型面带有一定的内凹形状，相应地上模带有一定的外凸形状。这样设计模具型面是由于压展过程中回弹现象是不可避免的，需要在模具型面上考虑一定程度的过弯，以抵消回弹对展平效果的影响。

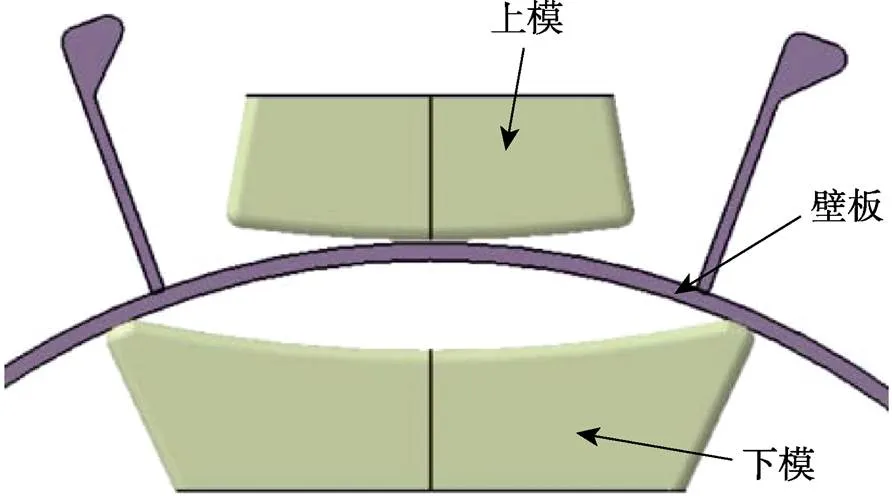
图2 模具型面示意

对壁板进行压弯或压展的过程中，回弹是影响加工精度的一个重要因素，回弹是材料在卸载后发生弹性回复造成的，目前对弯曲回弹过程已经有了较多的研究。有的研究者采用有限元方法结合试验验证，对回弹量进行预测计算。李小强等[3]对双相高强钢的Draw-bending试验进行了有限元仿真和试验研究，通过对比仿真与试验结果，得到了屈服模型和硬化模型对回弹预测的影响规律。王中秋等[4]对隔框类整体结构件的三点压弯校正过程进行了有限元仿真分析，得到了压弯残余变形量与载荷的关系。皇涛等[5]采用有限元仿真方法对高强钛管的弯曲回弹过程进行了研究，得到了弯曲角和相对弯曲半径对回弹角和回弹半径的影响规律。王大勇等[6]分析了U截面型钢压弯回弹过程，根据仿真和试验结果建立了半径回弹量与几个主要影响因素之间的回归预测模型。吴信涛等[7]对双相高强钢V形件的折弯回弹过程进行了分析，研究了各工艺参数对回弹量的影响规律，获得了优化的参数组合。

以上研究都是以有限元仿真手段为主。另外还有研究者，为弯曲回弹过程建立解析模型，从理论上分析回弹规律和影响因素。李明昕[8]针对一般性宽板弯曲回弹问题，分别建立了包含与不包含剪切应变的弯曲回弹解析模型，推导了弯矩和回弹角的求解方法，并与其他文献中宽板弯曲的试验结果进行了对比验证，分析了剪切应变的影响程度。赵长明[9]在宽厚板压弯回弹研究中，在截面应变场的表达式中考虑了剪切变形的影响，建立了厚板压弯回弹的预测模型，通过三点压弯试验，验证了回弹预测模型的准确性。刘静波等[10]建立了弯头半管冲压过程中的回弹预测模型，试验结果表明考虑剪切应变的模型计算准确性更高。李卫东等[11]建立了多种截面高筋壁板的压弯回弹预测模型，并与试验结果、有限元仿真结果进行了对比，结果表明理论模型计算结果的精度略差于有限元仿真结果，但仍具有较好的参考价值。周磊等[12]针对特定截面形状的T型导轨压弯回弹过程，分析了不同压弯方向下压弯回弹的截面力学关系，推导了压弯回弹曲率表达式，与试验结果进行了对比，发现解析计算结果具有较高的准确度。王安恒等[13]分析了Z型截面型材的中心层偏移情况，推导了回弹后弯曲半径的解析表达式，并与试验结果进行了对比，分析了中性层偏移对预测精度的影响。Ma等[14]研究了一般圆截面管的弯曲回弹问题，考虑了中性层内移、拉应力和压应力不对称分布和材料非线性等诸多影响因素，建立了回弹解析预测模型，并通过钛合金管的弯曲试验，验证了模型的有效性和准确性。Zhai等[15]研究了型材拉弯过程中的成形回弹问题，分析了拉、弯载荷共同作用下适用于任意截面形状的应力、应变规律，推导了回弹量计算的解析模型，并用有限元仿真以及试验方法验证了解析模型的有效性。Zou等[16]研究了带有预应变的弧形薄板的弯曲回弹过程，推导了预应变薄板进行同向和反向加载时的应力、应变分布，得到了回弹角和回弹后的曲率。Panthi等[17]分别基于应变法和能量法建立了厚板弯曲回弹过程的解析模型，同时建立了有限元仿真模型，与文献中的试验数据进行了对比分析，结果表明应变法模型的预测结果比能量法模型更接近试验结果，但两者精度都比有限元计算结果略差。

从上述的研究情况来看，对弯曲回弹过程的研究手段，主要包括建立理论模型进行解析计算，采用有限元方法进行过程仿真，以及试验研究。其中理论计算和有限元计算，都可以达到一定的精度，在不进行试验的情况下，给出一个较为准确的预测。因此，可采用建立理论解析模型和有限元仿真模型的方法，对该整体壁板压展过程进行分析，计算出可实现工艺目的的模具型面尺寸，作为模具设计制造的参考。

1 理论模型的建立和求解

1.1 基本假设

为简化分析过程，做如下假设：①垂直于中性层的截面，在弯曲回弹过程中，始终保持平面且垂直于中性层；②中性层位置不发生偏移，且周向长度保持不变；③只考虑沿圆周方向的正应变和正应力，忽略其他应变和应力；④忽略摩擦力；⑤材料拉伸变形与压缩变形中的应力-应变关系相似，且忽略包辛格效应，即：

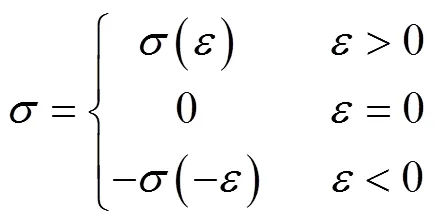
式中：为真实应变；为真实应力。和同时大于0或同时小于0，大于0时表示拉伸应变和拉伸应力，小于0时表示压缩应变和压缩应力。

1.2 变形过程分析

此处不考虑对筋条部位的压展方式，只研究腹板区域，所以问题就简化为带有初始弧度的宽厚板压展回弹过程。压展回弹过程包括3个典型状态：初始状态，加载状态和卸载状态，如图3所示。初始状态为壁板未发生变形时的状态，内部应力、应变为0。设此时的中性层曲率半径为0，长度为0，腹板厚度为，厚度方向为向，以中性层作为向点，则−/2≤≤/2。距离中性层为的层面（以下简称为层面），设其曲率半径为ρ0，长度为l0。加载状态是壁板在模具作用下达到最大变形，且尚未发生卸载的状态，设此时中性层曲率半径为A，长度为A，层面曲率半径为ρA，长度为lA。卸载状态是壁板在模具完全卸载后，发生回弹变形，达到最终形状时的状态，设此时的中性层曲率半径为B，长度为B，层面曲率半径为ρB，长度为lB。

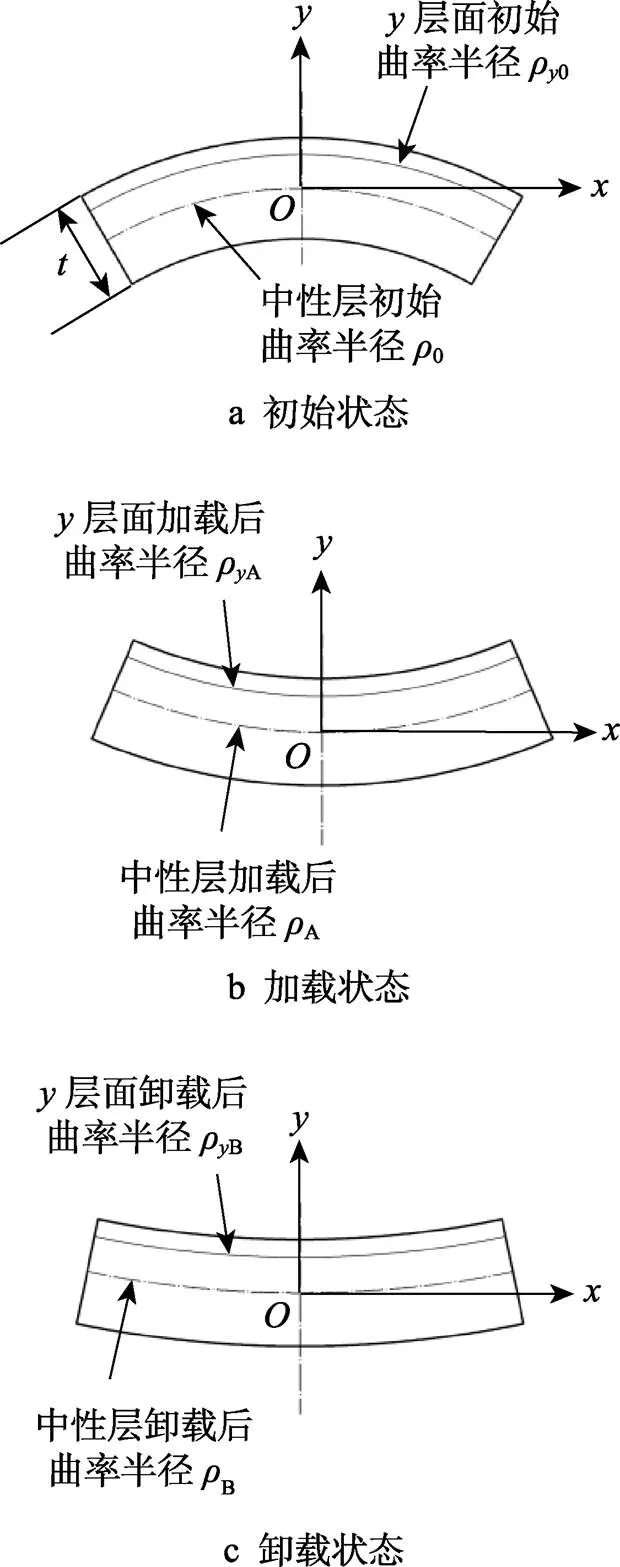
图3 截面状态示意

由层面与中性层之间的位置关系，可得到各曲率半径和层面长度之间的关系。

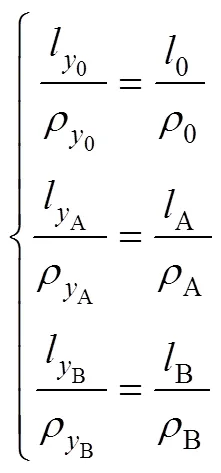
由图3可知各个状态下层面曲率半径与中性层曲率半径的几何关系为：

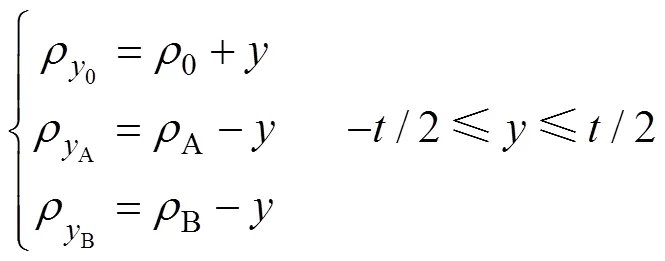
将式（3）带入式（2），同时考虑到中性层长度不变，即0=A=B，可得：

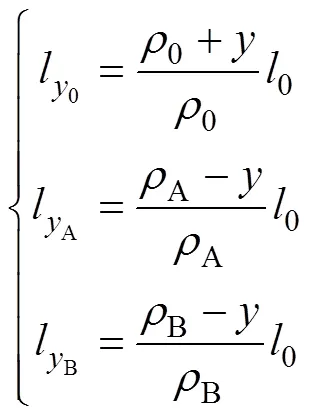
从初始状态到加载状态，层面的真实应变可表示为：

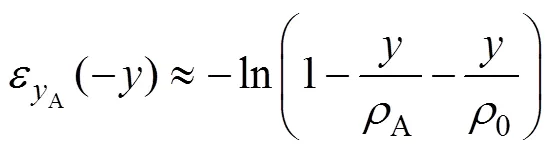
由式（7）和式（8）可近似认为：

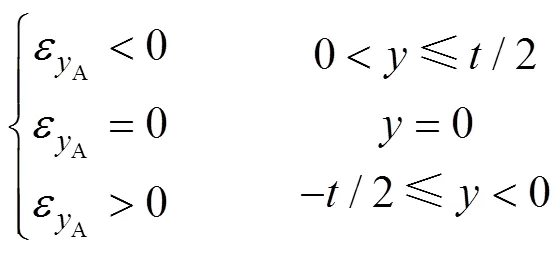
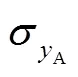
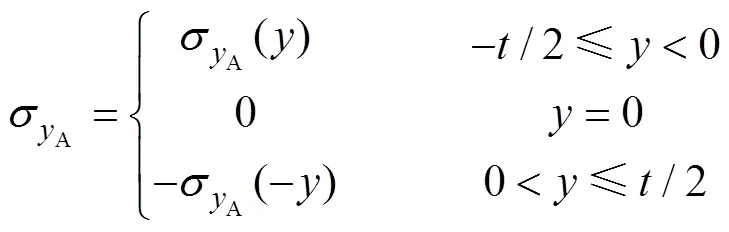
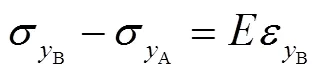
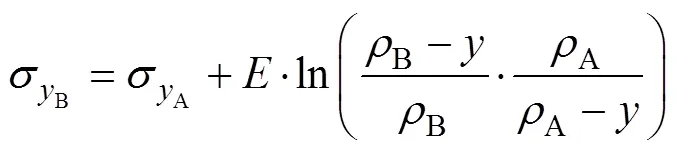
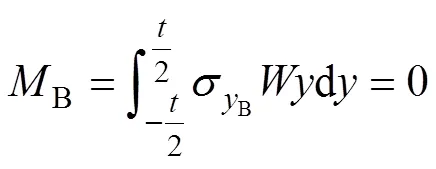
式中：B为残余应力引起的弯矩。考虑到式（10）、式（12—13），式（14）可改写为：

即：

1.3 材料的本构关系

壁板材料为1561铝合金，对该材料进行单拉试验，对试验数据进行处理和拟合。材料的真实应力-应变试验曲线及拟合曲线如图4所示。在一些文献中，为简化分析和计算过程，采用了线性材料模型[8-12,15-16]，但对于常见铝合金材料，线性材料模型有一定误差。为了对比材料模型对弯曲回弹过程计算结果的影响，此处同时采用线性模型，以及更加符合试验曲线的三次多项式模型，来描述材料的应力-应变关系。

图4 材料真实应力-应变试验曲线及拟合曲线

对材料的线性拟合结果为：

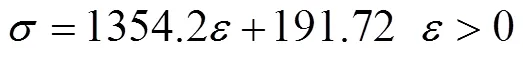
又因为式（1）中和的关系可得：

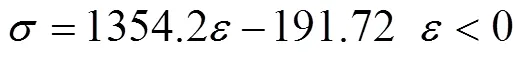
对材料的三次多项式拟合结果为：

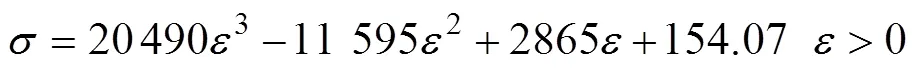
同样由式（1）可得：

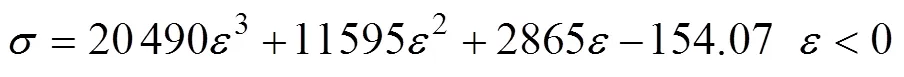
1.4 理论模型的求解

由式（5）、式（15）和式（17），可得到线性材料模型下的截面弯矩平衡方程：

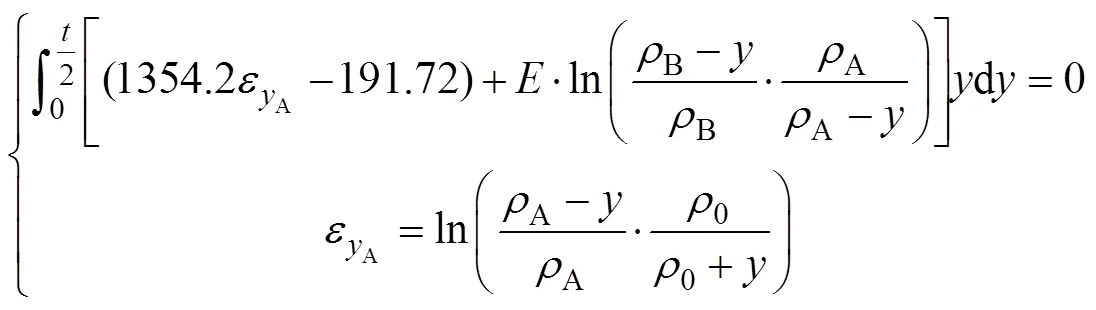
由式（5）、式（15）和式（19），可得到三次多项式拟合材料模型下的截面弯矩平衡方程：

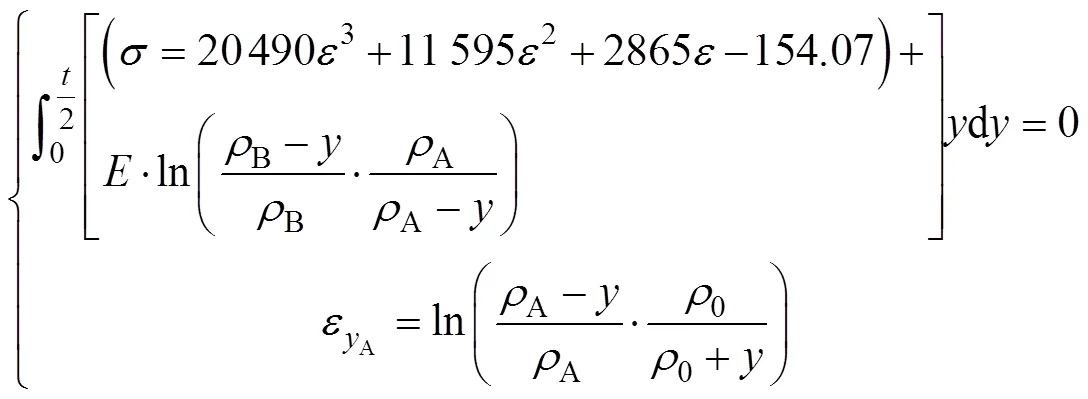
弹性模量，由单拉试验获得其值为68 GPa；0和为型材坯料的尺寸参数，随型材的规格不同而可能有所不同，但均可认为是已知量。A和B为未知量，式（20—21）反映了它们之间的关系。若给定其中一个量的值，则可通过数值方法求解出另一个量的值。其中A与模具型面曲率半径相差/2，是设计模具尺寸的关键量，B根据壁板的压展需求，其最佳值为趋于+∞。

对式（20—21）进行数值求解，其中取6 mm，0取250 mm。A和B的关系如图5所示。根据计算结果，若使腹板回弹后为平面，用2种不同材料模型计算的A分别是660 mm和745 mm。设两筋条之间可压展距离是150 mm，即模具型面的宽度不大于150 mm，考虑到圆角区域不能有效压展坯料，取有效压展区域宽度为140 mm。可计算得到有效压展区域型面的弧线拱高分别为3.72 mm和3.30 mm，前者相对于后者的相对误差为12.9%，该误差值可用来描述由这2种材料模型的不同所导致的模具型面设计误差。

图5 ρA和ρB关系的计算结果

若取值6 mm，B取值为+∞，材料模型选用三次多项式模型，改变0取值，可以得到0与A的关系，如图6所示。可以看到，A随0的增大而逐渐增大，两者为近似线性关系。当型材坯料的直径规格发生变化时，可根据该曲线直接获得A值，进而确定了模具型面尺寸。

图6 ρ0和ρA关系的计算结果

2 有限元仿真验证

2.1 有限元模型的建立

在有限元软件中建立压展回弹过程的有限元模型，对上述理论分析的结果进行验证。建模过程中，做如下3项简化：①选取型材截面的一部分，即从截面的完整圆中截取一部分，由于每次压制只在相邻筋条之间进行，变形区域相对较小，且此时型材已被剖开，截面为开口，因此无需计算完整截面，选取筋条间距约3倍弧长，典型截面的筋条间距约180 mm，这里取弧长为540 mm，圆弧半径取250 mm；②忽略筋条，由于筋条在压展区域以外，对压展过程中变形区域的影响很小，建模时将其忽略；③采用二维模型，型材长度远大于腹板厚度，因此可认为变形过程中材料处于平面应变状态。

取腹板厚度为6 mm，下模为凹模，型面曲率半径为748 mm，上模为凸模，型面曲率半径为742 mm。凹模宽度较宽，将边缘型面设计为坯料型材原始型面尺寸，用于托举定位。凸模宽度较窄，考虑到筋条间距，取凸模总宽度为150 mm，型面边缘圆角半径为5 mm，因此有效压展区域宽度约140 mm。基于前述几条简化，建立有限元模型，如图7所示。材料的塑性数据由三次多项式拟合的材料模型计算得到。

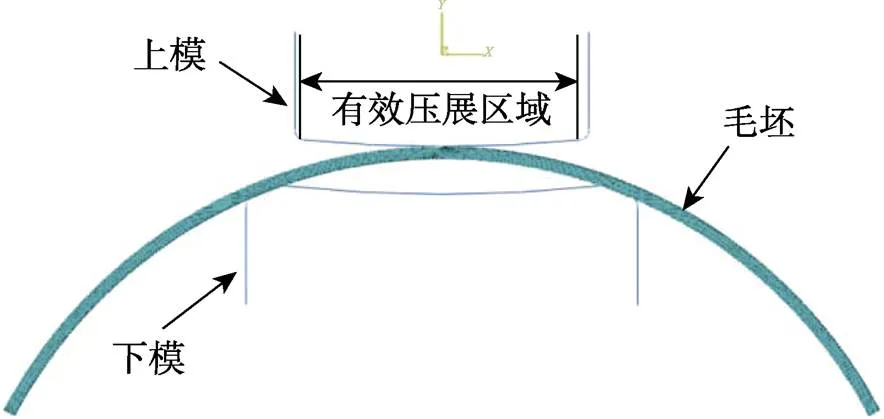
图7 有限元模型

2.2 有限元仿真结果

利用以上有限元模型对压展回弹过程进行仿真，加载过程中控制凸、凹模间隙为6 mm，仿真结果如图8所示。

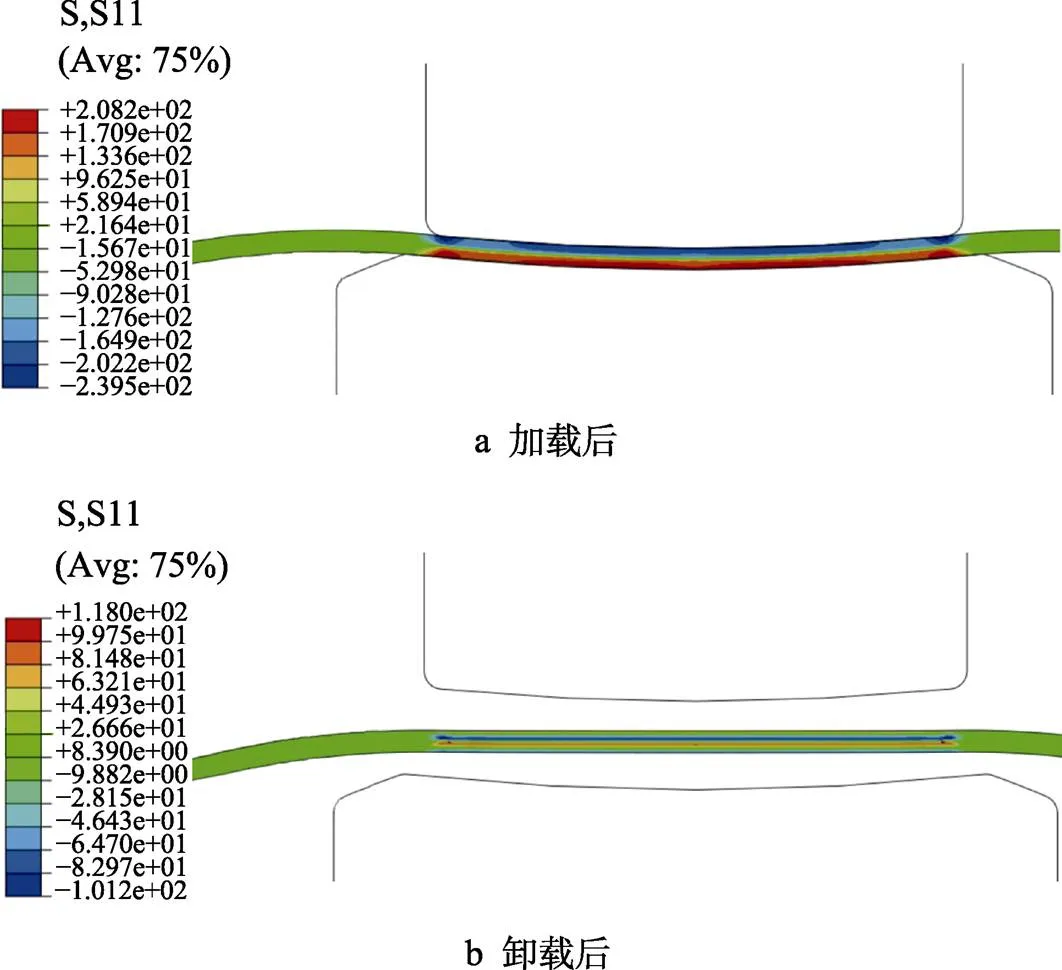
图8 有限元仿真结果（mm）

从图8b可以看到，壁板在压展回弹后，展平效果良好。提取有限元结果中壁板表面节点在卸载回弹后的坐标，计算各节点偏离平面的距离来衡量展平效果。这里提取上表面节点。以中心节点为基准点，由于模型对称，取右侧数据，如图9所示，其中数值0.1502 mm即为有效压展区域内对于基准平面的最大偏离值，该值即为腹板的平面度误差。

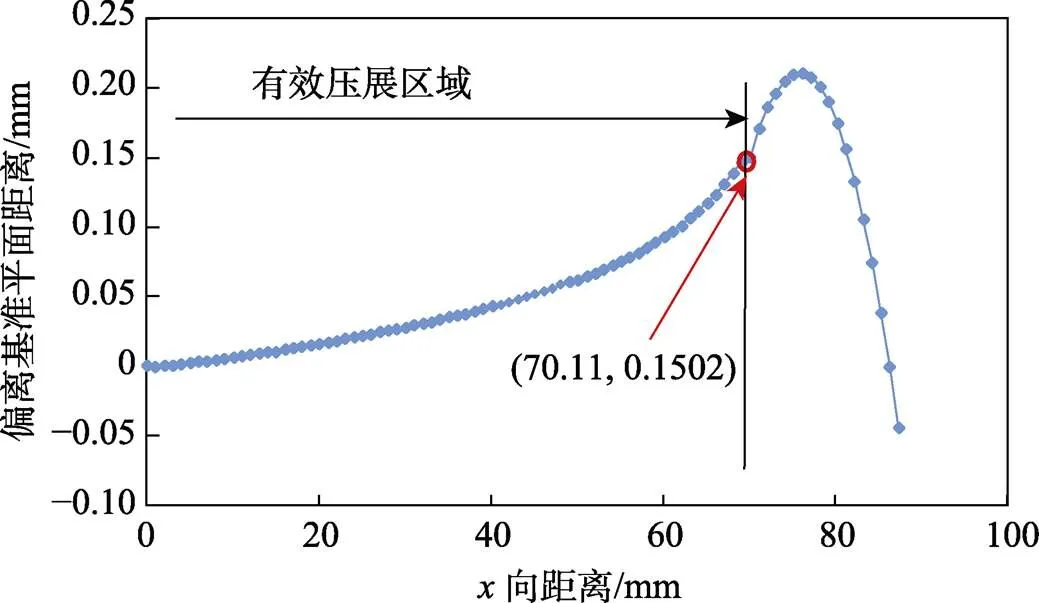
图9 压展回弹后壁板表面偏离平面的距离

改变模具型面半径，进一步对图5中的A和B关系进行仿真验证。有限元仿真结果与采用三次多项式材料模型的理论计算结果对比情况如图10a所示。为了更直观地反映模具型面的差异，将B的对比转换成140 mm弦长情况下弧线拱高的对比，如图10b所示。

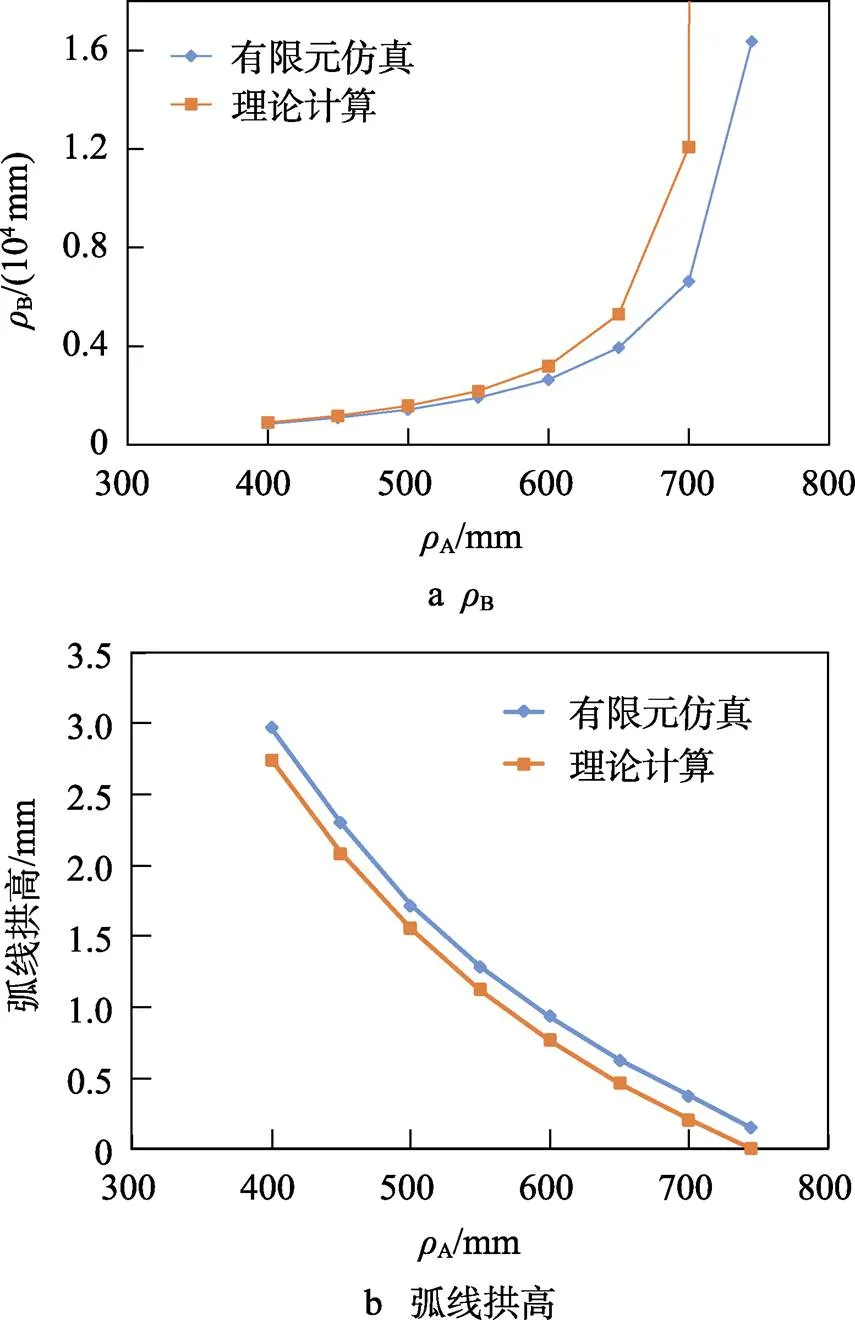
图10 有限元仿真与理论计算结果对比

2.3 结果对比分析

从有限元仿真与理论计算结果来看，两者符合得比较好，这表明在求解圆弧壁板压展回弹问题时，理论计算方法是可行的，与有限元仿真方法具有相似的准确性。具体到对展平效果的计算，即在回弹后壁板为平面的情况，在140 mm的宽度上误差只有约0.15 mm，足以满足该工序的需要。

从对不同模具型面的计算结果来看，理论计算与有限元仿真结果的误差有明显规律性。图10a显示，B的误差随着A的增大而增大，但在弧线弦长一定的情况下，A较大时，即使A数值变化较大，弧线的变化也并不明显。从图10b的弧线拱高对比上可以看出，拱高的误差是比较稳定的，如图11所示，在0.15～0.23 mm之间，且随着A的增大，大致呈缓慢下降的趋势。这表明两者的计算误差应该是系统误差，由于材料模型一致，造成系统误差的原因应该是应力、应变状态与分布等力学方面的多个简化假设。

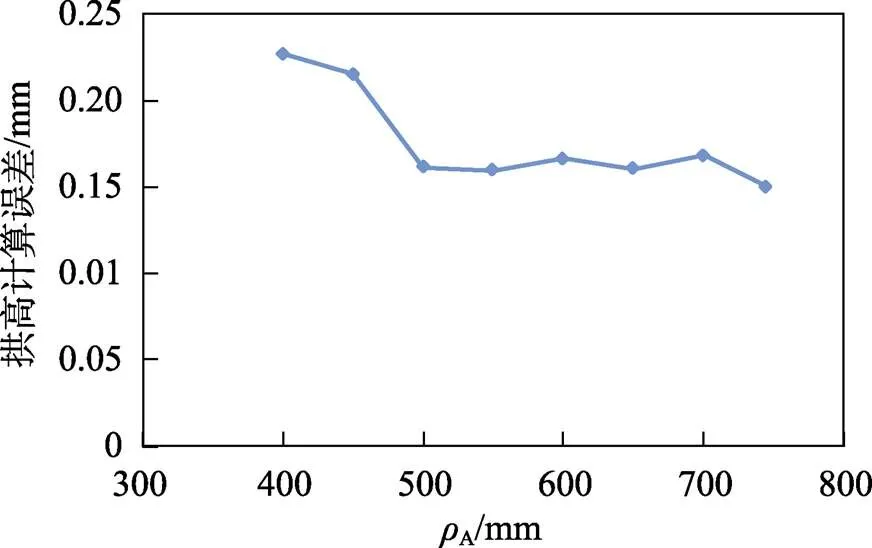
图11 理论计算与有限元仿真的弧线拱高误差

3 试验验证

对前述理论分析的结论进行试验验证。试验材料选用成品的挤压管材，特征尺寸为外径为400 mm，厚度为10 mm，即0为195 mm，为10 mm。管材材料为铝合金6061T6。首先在管材上取样，进行单向拉伸试验，以获得材料的应力、应变关系，单向拉伸试验结果如图12所示。采用三次多项式对材料塑性变形阶段的应力-应变曲线进行拟合，拟合结果见式（22）。

由式（1）中和的关系可得：

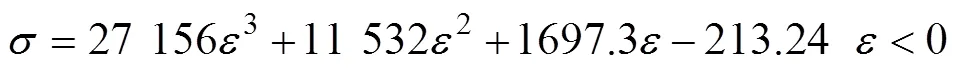
试验中采用的模具型面为半径为400 mm的圆柱面，即A为395 mm。用于压弯的试件取样方式为，沿圆周方向取弦长为200 mm的弧段，即对应弧长0为210 mm；沿轴向取100 mm，即为100 mm。试验情况如图13所示。

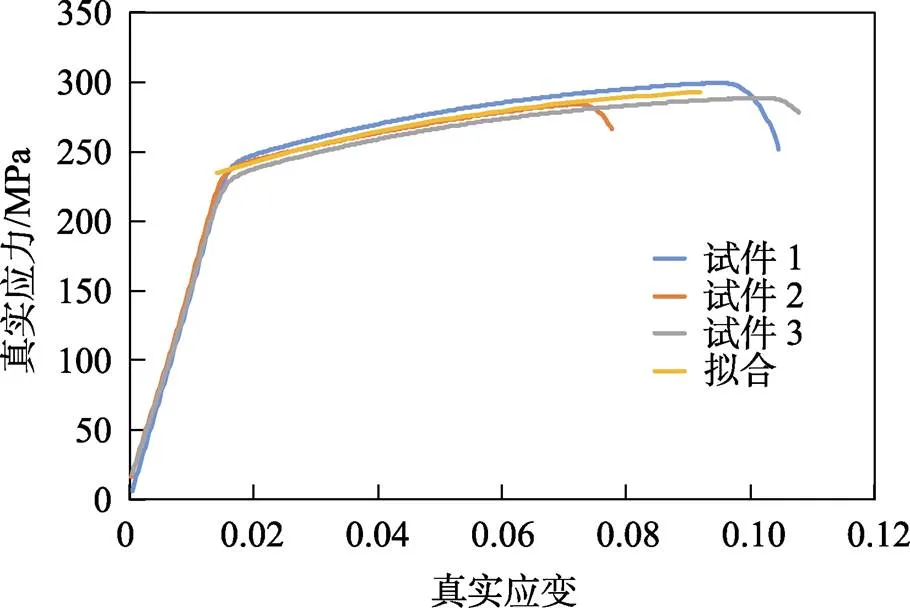
图12 单拉试验结果

图13 压弯试验

将验证试验中试件的各几何参数及材料参数代入式（15），采用数值解法得到卸载后试件的半径B为692.5 mm。对试验后试件的曲率进行测量。曲率测量位置如图13d所示，以弧长中心位置为起始点，向两侧每间隔20 mm设置一个测量点，一列共9个测量点，垂直于弧长方向，每26 mm设置一列测量点，共设置4列。试验后采用数显半径规仪对试件曲率进行测量，测量跨度选用30 mm规格。测量时读取跨度内的拱高作为直接测量结果，然后换算为曲率半径。将4列测量点中相同位置的测量值进行平均，作为该位置的测量结果，如图14所示。

从测量结果与理论计算值的对比来看，除中间位置外，其他测量点的试验值与计算值符合得相对较好，这表明通过理论计算得到的结果可以达到一定的精度。中间测量点的测量值偏离理论计算结果较多，可能与变形过程有关。该位置在加载过程中首先与凸模接触而率先发生变形，而卸载过程中又是最后与凸模脱离接触，其变形过程中内部的应力、应变变化较两侧更为复杂。文中理论计算方法只研究了3种变形状态，而忽略了不同变形状态之间发展演化的过程对材料内部应力、应变的影响，这也就造成了材料中间位置的计算结果误差更大。

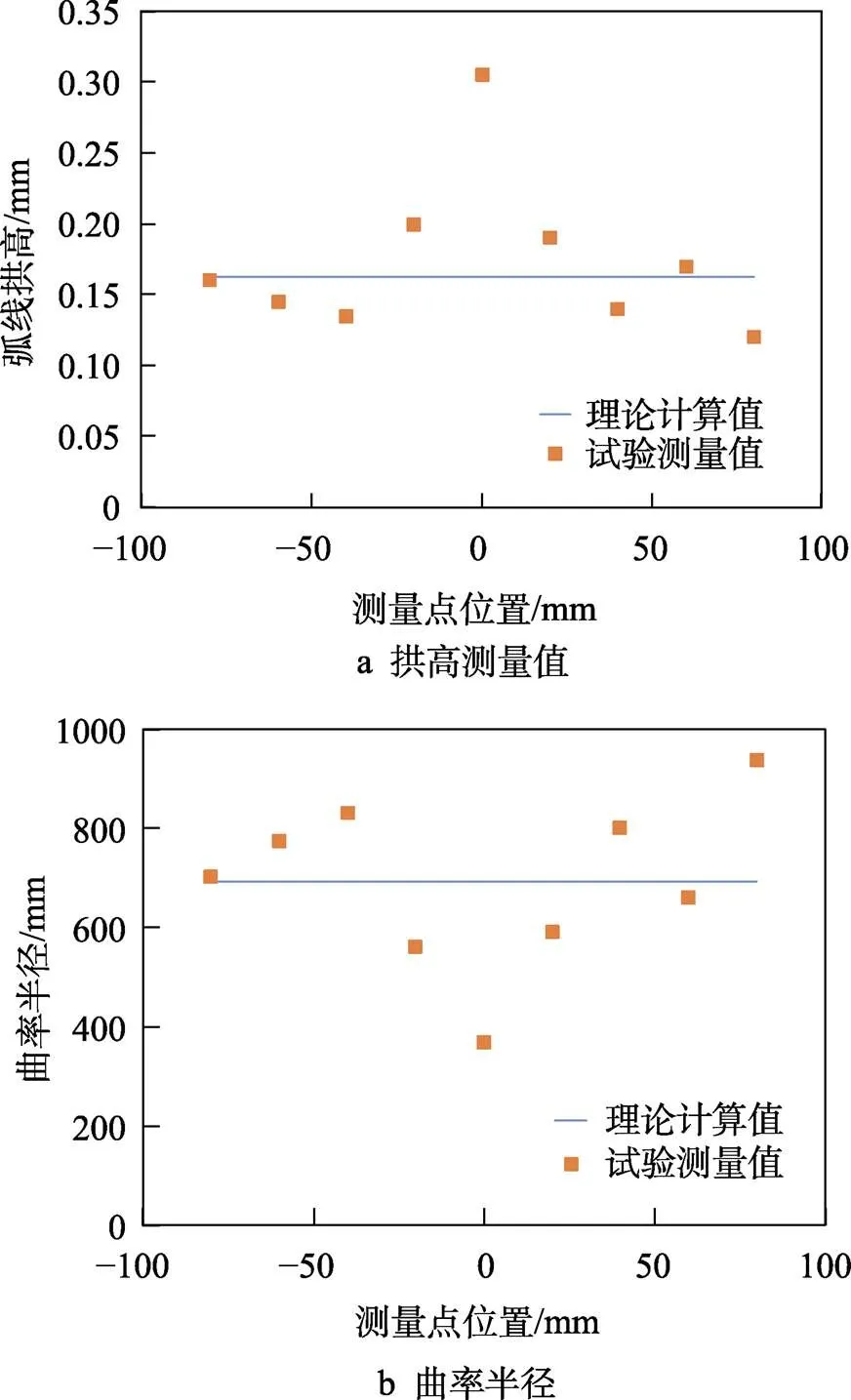
图14 测量结果

4 结论

1）以平行于中性层的层面在压展回弹过程中的长度变化规律作为依据，推导了中性层在加载情况下与卸载回弹后曲率半径之间的关系，并通过数值解法得到了初始曲率、加载曲率和卸载后曲率之间的数值对应关系，可作为模具型面尺寸设计的依据。

2）材料模型对理论计算结果有一定的影响，为提高计算精度，应选取更为准确描述材料应力-应变关系的模型。

3）利用有限元仿真方法和试验对理论推导的结果进行了验证，一致性较好，表明理论计算的准确性与有限元仿真相当，而理论计算值与试验结果在大部分区域准确性较好，但在中心位置误差较大。同时，理论计算与有限元仿真之间也存在着系统性误差，误差值较稳定。针对误差存在的原因可开展进一步的研究。

[1] 王端志, 胡勇, 孙海霞, 等. 高强韧铝合金结构壁板研究进展[J]. 强度与环境, 2020, 47(5): 28-36.

WANG Duan-zhi, HU Yong, SUN Hai-xia, et al. Research of High-Strength and Toughness Aluminum Structural Panels for Aerospace and Warship[J]. Structure & Environment Engineering, 2020, 47(5): 28-36.

[2] 李靖. 7B04铝合金整体壁板多点压弯成形的失稳研究[D]. 长春: 吉林大学, 2017: 2-4.

LI Jing. Research on Buckling of 7B04 Aluminum Alloy Integral Panel Using Multi-Point Dies[D]. Changchun: Jilin University, 2017: 2-4.

[3] 李小强, 董红瑞, 于长旺, 等. 不同屈服准则与硬化模型对DP780双相高强钢拉延弯曲回弹预测影响规律研究[J]. 机械工程学报, 2020, 56(12): 42-55.

LI Xiao-qiang, DONG Hong-rui, YU Chang-wang, et al. Influence of Yield Criteria and Hardening Model on Draw-Bending Springback Prediction of DP780[J]. Journal of Mechanical Engineering, 2020, 56(12): 42-55.

[4] 王中秋, 李剑峰, 孙杰, 等. 基于回弹曲线的航空整体结构件三点压弯校正分析[J]. 山东大学学报: 工学版, 2009, 39(2): 78-81.

WANG Zhong-qiu, LI Jian-feng, SUN Jie, et al. Three-Point Press Straightening Analysis of Aircraft Monolithic Component Based on Its Rebound Curve[J]. Journal of Shandong University: Engineering Science, 2009, 39(2): 78-81.

[5] 皇涛, 王锟, 詹梅, 等. 考虑材料参数变化的高强钛管数控弯曲回弹行为研究[J]. 精密成形工程, 2019, 11(4): 97-103.

HUANG Tao, WANG Kun, ZHAN Mei, et al. Springback Behavior of High Strength Titanium Tube in Numerical Control Bending Considering Variation of Material Parameters[J]. Journal of Netshape Forming Engineering, 2019, 11(4): 97-103.

[6] 王大勇, 傅利斌, 李伟, 等. U截面型钢压弯回弹的试验研究及预测分析[J]. 锻压技术, 2011, 36(1): 140-143.

WANG Da-yong, FU Li-bin, LI Wei, et al. Test and Prediction Study of U-Section Channel in Press Bending Springback Process[J]. Forging & Stamping Technology, 2011, 36(1): 140-143.

[7] 吴信涛, 丁方强, 刘国凯, 等. DP800双相高强钢折弯及回弹研究[J]. 精密成形工程, 2016, 7(4): 38-42.

WU Xin-tao, DING Fang-qiang, LIU Guo-kai, et al. Bending and Springback of High-Strength Dual Phase Steel DP800[J]. Journal of Netshape Forming Engineering, 2016, 7(4): 38-42.

[8] 李明昕. 宽厚板弯曲回弹解析模型研究[D]. 大连: 大连理工大学, 2019: 10-25.

LI Ming-xin. Research on Analytical Model for Bending Springback of Wide Heavy Plates[D]. Dalian: Dalian University of Technology, 2019: 10-25.

[9] 赵长明. 宽厚板压弯回弹预测模型研究[D]. 秦皇岛: 燕山大学, 2016: 8-49.

ZHAO Chang-ming. Study on Prediction Model of Plate Bending Springback[D]. Qinhuangdao: Yanshan University, 2016: 8-49.

[10] 刘静波, 段明德, 张壮雅, 等. 90°弯头half厚板压弯回弹预测[J]. 锻压技术, 2019, 44(10): 71-78.

LIU Jing-bo, DUAN Ming-de, ZHANG Zhuang-ya, et al. Bending Springback Prediction on 90° Elbow Half Plate[J]. Forging & Stamping Technology, 2019, 44(10): 71-78.

[11] 李卫东, 万敏, 阎昱. 整体壁板压弯成形中性层及回弹解析[J]. 塑性工程学报, 2014, 21(5): 156-161.

LI Wei-dong, WAN Min, YAN Yu. Neutral Layer and Springback Analysis in Press Bend Forming of Aircraft Integral Panels[J]. Journal of Plasticity Engineering, 2014, 21(5): 156-161.

[12] 周磊, 余忠华, 胡志辉, 等. T型导轨二维压弯回弹解析与试验[J]. 浙江大学学报: 工学版, 2011, 45(8): 1360-1365.

ZHOU Lei, YU Zhong-hua, HU Zhi-hui, et al. Two-Dimensional Bending Springback Analysis and Test of T-Rail[J]. Journal of Zhejiang University: Engineering Science, 2011, 45(8): 1360-1365.

[13] 王安恒, 薛红前, 杨艳丽, 等. 基于中性层偏移的Z型材滚弯成形回弹预测[J]. 航空学报, 2019, 40(12): 259-268.

WANG An-heng, XUE Hong-qian, YANG Yan-li, et al. Springback Prediction for Z-Shaped Profiles in Roll Bending Process Based on Neutral Layer Shift[J]. Acta Aeronautica et Astronautica Sinica, 2019, 40(12): 259-268.

[14] MA Jun, LI Heng, FU Ming-wang. Modelling of Springback in Tube Bending: A Generalized Analytical Approach[J]. International Journal of Mechanical Sciences, 2021, 204: 106516-1-106516-15.

[15] ZHAI Rui-xue, DING Xue-hui, YU Shu-man, et al. Stretch Bending and Springback of Profile in the Loading Method of Prebending and Tension[J]. International Journal of Mechanical Sciences, 2018, 144: 746-764.

[16] ZOU Tian-xia, XIN Ji-yuan, LI Da-yong, et al. Analytical Approach of Springback of Arced Thin Plates Bending[C]// 11th International Conference on Technology of Plasticity, Nagoya, 2014, 81: 993-998.

[17] PANTHI S K, RAMAKRISHNAN N. Semi Analytical Modeling of Springback in Arc Bending and Effect of Forming Load[J]. Transactions of Nonferrous Metals Society of China, 2011, 21: 2276-2284.

Obtaining of Tool Surface Curvature Radius for Bending and Flattening Integral Panel

HAN Jin-quan1, WANG Shao-hua2, LIU Hui2

(1. School of Mechanical Engineering and Automation, Beihang University, Beijing 100191, China; 2. AECC Beijing Institute of Aeronautical Materials, Beijing 100095, China)

The work aims to study the deformation and springback rule of integral panel with initial curvature during bending and flattening process to determine the curvature radius of tool surface. The deformation of material in the circumferential direction of section was described in three states of initial, loading and unloading. The distributions of strain and stress and the equilibrium conditions after unloading were deduced to obtain the relationship among the initial curvature radius, loading curvature radius and the springback curvature radius after unloading. Then, finite element simulation and experiment were conducted to verify the deduced result. In addition, the comparison of analytical results with different material models by numerical calculation showed that the accuracy of the material model had a certain impact on the calculation results. The numerical relationship between the initial curvature radius and the loading curvature radius for a given springback curvature radius, and the numerical relationship between the loading curvature radius and the springback curvature radius for a given initial curvature radius were obtained. The accuracy of the latter was verified by finite element simulation and results. The results obtained through theoretical derivation of bending and flattening process of integral panel are accurate enough to describe the variation law of the curvature radius, which can be used as the basis when design the tool surface.

integral panel; bending and flattening; springback; strain distribution

10.3969/j.issn.1674-6457.2022.03.002

TG386

A

1674-6457(2022)03-0008-09

2021-08-05

GF基础科研项目

韩金全（1980—），男，博士，讲师，主要研究方向为航空薄壁结构件精密成形技术。