基于观测器的车辆电子稳定控制系统执行器故障重构

王宏伟, 王倩玉, 韩 杰, 张昊天

(东北大学秦皇岛分校 控制工程学院, 河北 秦皇岛 066004)

随着经济发展和生活水平的提高,我国机动车保有量逐年上升.汽车带来生活便利的同时也造成很多交通事故,给人们的生命和财产造成巨大损失.车辆电子稳定控制(electronic stability control, ESC)系统是主动安全技术的重要组成部分,能够在事故发生前发现隐患并消除,有效改善汽车行驶的稳定性和安全性[1].执行器是ESC系统的重要组成部分,由于频繁使用,出现故障较为常见,一旦发生故障,会影响车轮轮胎力的变化,导致ESC不能发挥应有的作用,影响车辆的安全性.因此,对ESC系统执行器故障诊断研究具有重要意义.

近年来,国内外学者广泛关注控制系统执行器故障,并取得丰富的研究成果[2-4].目前,对汽车ESC系统执行器故障的研究成果相对较少.文献[5]针对汽车ESC系统,基于执行器故障増广系统模型设计观测器,但模型中未考虑实际系统存在不确定因素的影响.文献[6]考虑了车辆运行中侧风的影响,针对ESC系统设计故障诊断算法,根据残差进行故障诊断[6].但文献[5-6]研究对象为前轮转向系统,考虑到前轮转向系统自身结构设计所存在的问题逐渐不能满足人们对车辆稳定性的要求,部分学者对四轮转向系统进行深入研究.文献[7-8]针对四轮转向系统模型中存在不确定性因素,设计优化的控制策略改善车辆的操控性.文献[9]提出一种基于路面附着系数的四轮转向系统与电子稳定程序协调控制方法,提高极端条件下车辆的稳定性.文献[7-9]均未考虑执行器发生故障的情况.考虑到执行器故障的发生,文献[10]将后轮转向和ESC系统相结合,设计状态估计器,但未考虑系统存在不确定因素.

针对上述问题,考虑ESC四轮转向系统中存在不确定因素以及执行器故障,设计基于观测器的故障诊断算法,并给出理论证明.将MATLAB/ Simulink与Carsim在复杂行驶工况下进行联合仿真,验证所设计观测器的有效性.

1 二自由度汽车模型

为了分析车辆在行驶过程中的操纵稳定特性,将汽车模型简化为二自由度模型,如图1所示[8].

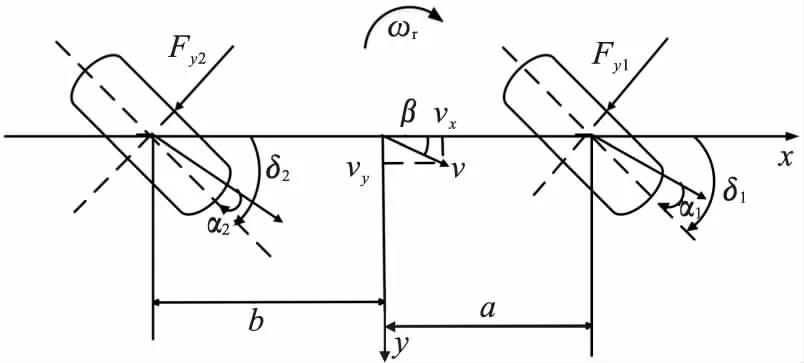
图1 二自由度四轮转向汽车模型

图中:Fy1和Fy2分别为前后轮所受地面侧向反作用力;δ1和δ2分别为前后轮输入的转角;α1和α2分别为前后轮的侧偏角;ωr为汽车的横摆角速度;β为整车的质心侧偏角;vx和vy分别为汽车纵向车速和横向车速;a和b分别为质心到前后轮的距离.

对模型进行受力和运动分析,二自由度汽车受外力沿y轴方向的合力以及绕质心的力矩为

(1)

依据牛顿第二定律,式(1)可以化简为

(2)

式中:m为汽车的质量;Iz为绕z轴的转动惯量.

根据轮胎的侧偏特性,有

(3)

式中:k1为前轮的侧偏刚度;k2为后轮的侧偏刚度.

根据几何关系及运动分析,得

(4)

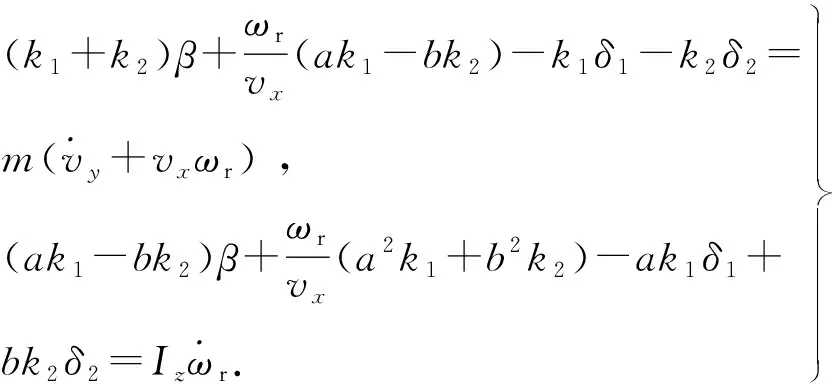
(5)

整理式(5),得

(6)

四轮转向汽车二自由度标准状态空间方程为

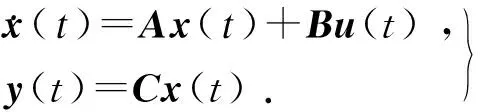
(7)

式中:x(t)=[ωrβ]T为系统的状态向量;系统的控制输入为u(t)=[δ1δ2]T;y(t)为系统的输出;A,B,C为适当维数的系数矩阵,

2 基于不确定车辆ESC系统执行器故障设计观测器

考虑到实际智能汽车行驶环境复杂,系统中存在诸多不确定因素,系统的状态矩阵和参数也存在变化,因此针对不确定车辆ESC系统,将执行器故障引入车辆模型中,通过设计观测器来实现执行器故障重构.

2.1 不确定车辆稳定系统执行器故障数学模型

考虑如下不确定系统模型:

(8)

式中:ΔA和ΔB为系统的不确定项,分别满足ΔA=D1F1E1,ΔB=D2F2E2,D1,D2,E1和E2是已知适当维数的常数矩阵,Fi为未知矩阵,满足‖Fi‖≤I,i=1,2.

引理1[11]若存在相同维数的实数向量x,y,则对于任意正数α,有下面的不等式成立:

±2xTy≤αxTx+α-1yTy.

(9)

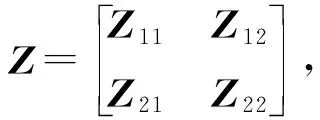
(10)

当执行器发生故障时,状态方程(8)可写成如下形式:

(11)

式中:fa为执行器故障;Ea为故障矩阵.

将故障作为一个状态变量,建立如下形式的数学模型:

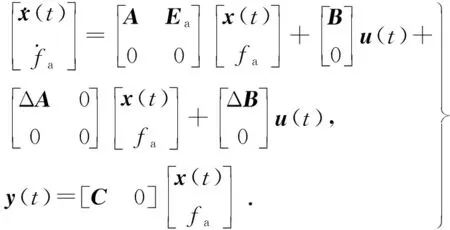
(12)

重构后的状态空间方程为

(13)

2.2 设计观测器

针对不确定系统(13),设计如下形式观测器:

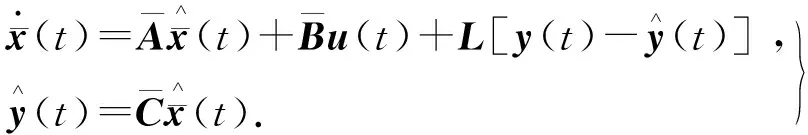
(14)

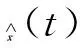
定义系统状态误差为

(15)

对式(15)求导,将式(13)和(14)代入式(15),得

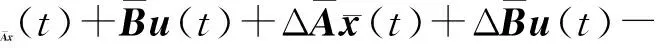
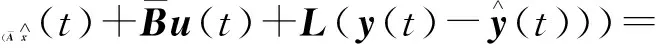
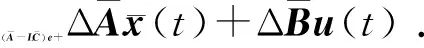
(16)

本文选择基于观测器的状态反馈控制器为

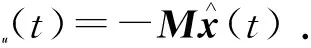
(17)

式中,M为控制器的增益矩阵.则有

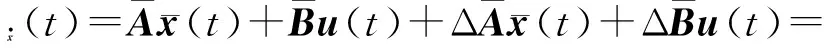
(18)

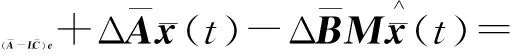
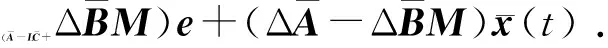
(19)

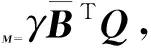
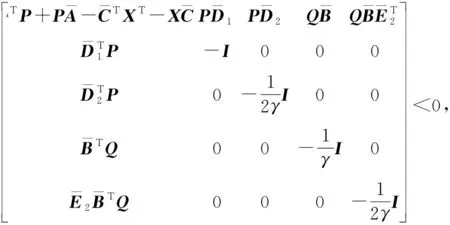
(20)

(21)

则式(14)所设计的观测器是稳定的,并且观测器增益满足L=P-1X.

证明 选取Lyapunov函数

(22)

式中P和Q均为对称正定矩阵.

对式(22)进行求导,得

(23)

将式(19)代入式(23)中,得

(24)

根据引理1,并且令α=1,则

(25)

(26)

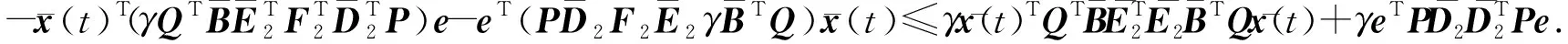
(27)

将式(25)～(27)代入式(24),得

(28)

将式(18),式(19)代入式(23)中,得

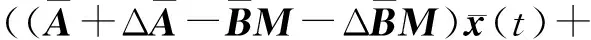
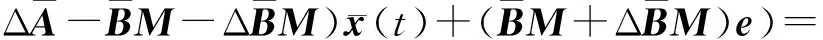
(29)

根据引理1,并且令α=1,则

(30)

(31)

将式(30)～(31)代入式(29),化简为

(32)

根据式(28)和式(32)可以得到

(33)

式中:

(34)

(35)

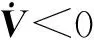
3 仿真研究

本文利用MATLAB/Simulink与Carsim联合对车辆ESC系统进行仿真分析,模拟多种极限工况,选择Carsim软件中C-Class Hatchback车型.具体参数如下:m=1 274 kg,Iz=1 523 kg·m2,k1=-84 800 N/rad,k2=-144 000 N/rad,a=1.016 m,b=1.562 m,g=9.8 m/s2.不确定参数选择如下:D1=D2=[2 1]T,E1=[0 5],E2=5,F1=F2=0.1,γ=1.仿真选取的初始车速为vx=120 km/h,vy=0,在双移线工况下进行仿真.利用车辆参数,编写程序求得观测器增益矩阵L,

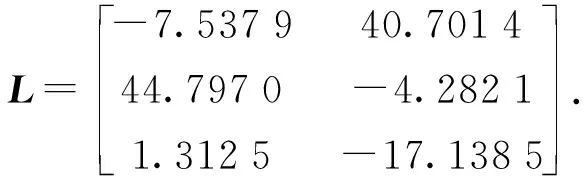
通过在相同车速不同附着系数的双移线工况下仿真,假设执行器在第2～3 s及5～6 s发生故障,故障形式如下:

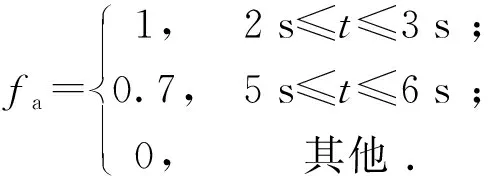
工况1vx=120 km/h,附着系数μ=0.5的湿滑路面.

车辆在双移线工况下行驶时,前后轮的转角曲线如图2所示.横摆角速度和质心侧偏角变化曲线分别为图3和图4.由图中可以看出:车辆在湿滑路面双移线工况下,横摆角速度和质心侧偏角的估计值能很好地追踪上真实值.当执行器在第2～3 s和5～6 s发生故障时,存在一定的误差,但很快估计值能够追踪上真实值,实现故障诊断的目的,同时保证车辆稳定行驶.

与前轮转向系统相比,四轮转向系统中前后轮共同参与运动,能减少前后轮之间存在的误差,增加车辆的稳定性.在高速行驶时,采用四轮转向系统能够减少车辆侧翻等危险事故的发生,从而增加行驶安全.

图2 前后轮转角输入曲线(μ=0.5)

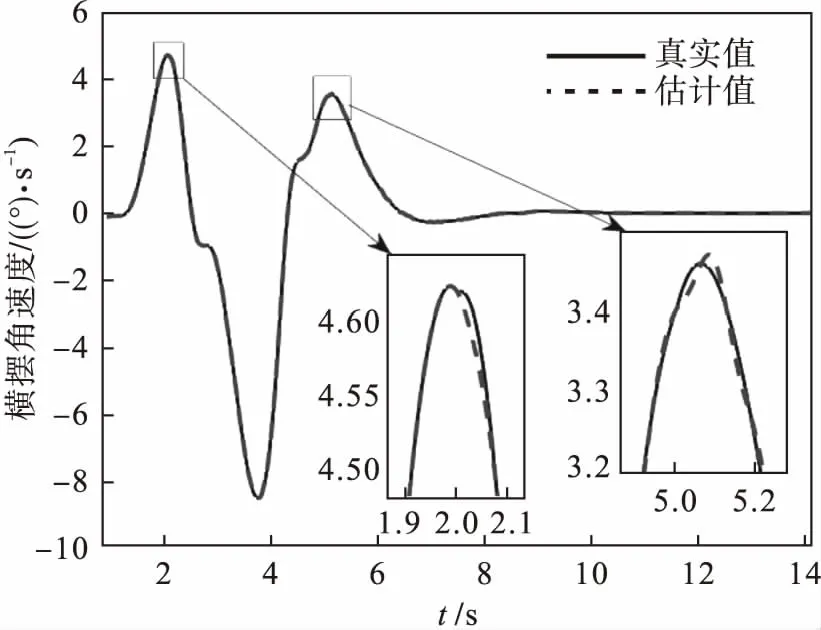
图3 横摆角速度变化曲线(μ=0.5)

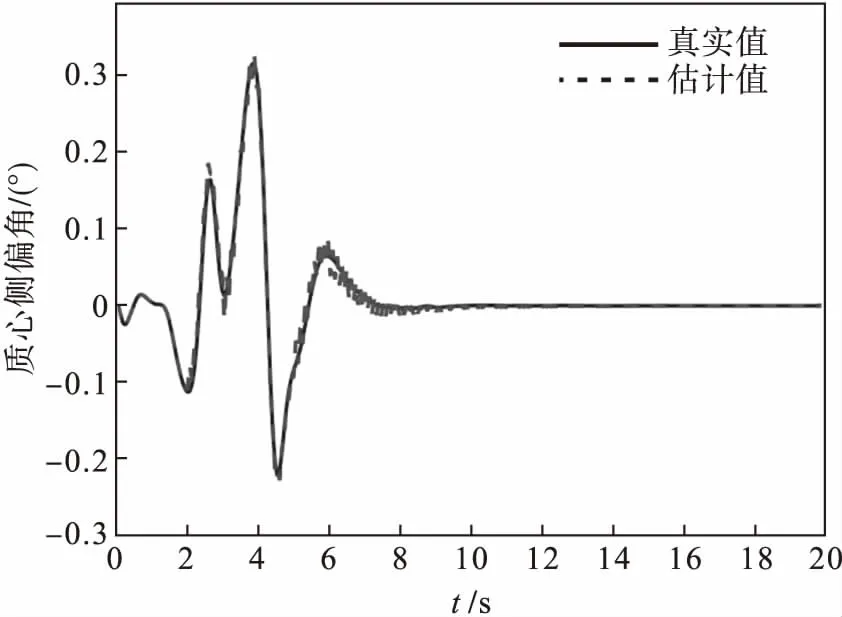
图4 质心侧偏角变化曲线(μ=0.5)

图5和图6为在相同行驶条件下,四轮转向与前轮转向的横摆角速度和质心侧偏角对比曲线.图5中2条曲线到达稳定的时间基本相同,采用前轮转向控制的横摆角速度幅值在-9.4～5.6(°)/s,而四轮转向系统的横摆角速度幅值在-8.7～4.7(°)/s,由于四轮转向系统的前后轮同时参与转向,使得横摆角速度的幅值减小、车辆的灵敏性增强、超调量更小,转向运动更加平稳.同时,在高速运行时需要驾驶员多打方向盘,既降低了驾驶员误打方向盘的危险性,又增加了汽车的主动安全性.从图6中可以看出,采用四轮转向系统的质心侧偏角幅值明显减小,前轮控制的质心侧偏角转动范围在-0.34°～0.57°,经过10 s左右的波动,最后在零值附近达到稳定状态；采用四轮转向的质心侧偏角转动范围在-0.23°～0.32°,经过8 s后质心侧偏角稳定为0,即没有侧向运动,说明四轮转向系统能够显著改善质心侧偏角,且更快到达稳定,增强高速运行时车辆的稳定性.

图5 横摆角速度响应曲线(μ=0.5)

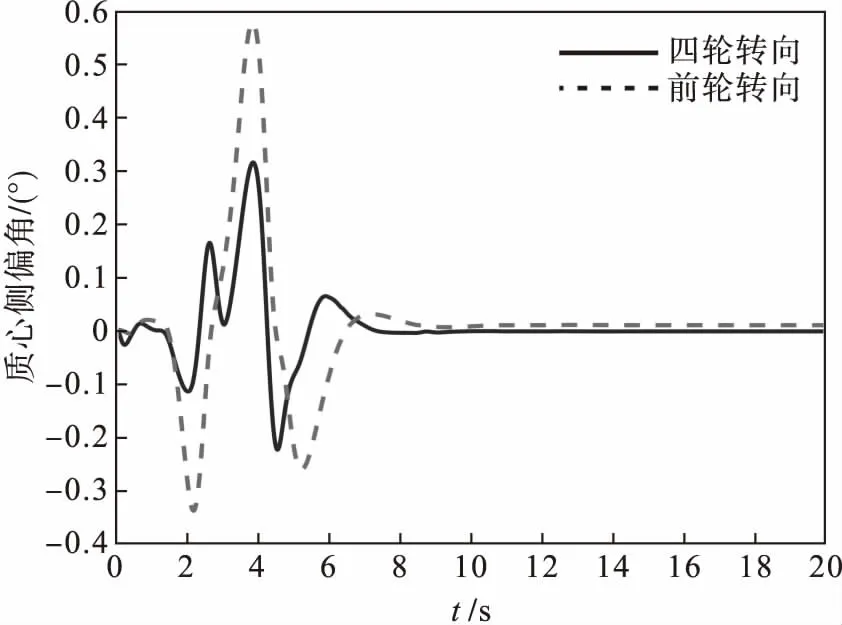
图6 质心侧偏角响应(μ=0.5)

工况2vx=120 km/h,μ=0.2的冰雪路面.

为了模拟多种复杂工况下的观测效果,更准确对车辆在极限状况下运行稳定性进行分析,采用附着系数为0.2的冰雪路面工况,其他仿真条件不变.车辆前后轮转角输入曲线如图7所示.

针对冰雪路面的恶劣环境,横摆角速度和质心侧偏角仿真结果如图8和图9所示.横摆角速度及质心侧偏角真实值与估计值的误差如图10和图11所示.

图7 前后轮转角输入曲线(μ=0.2)

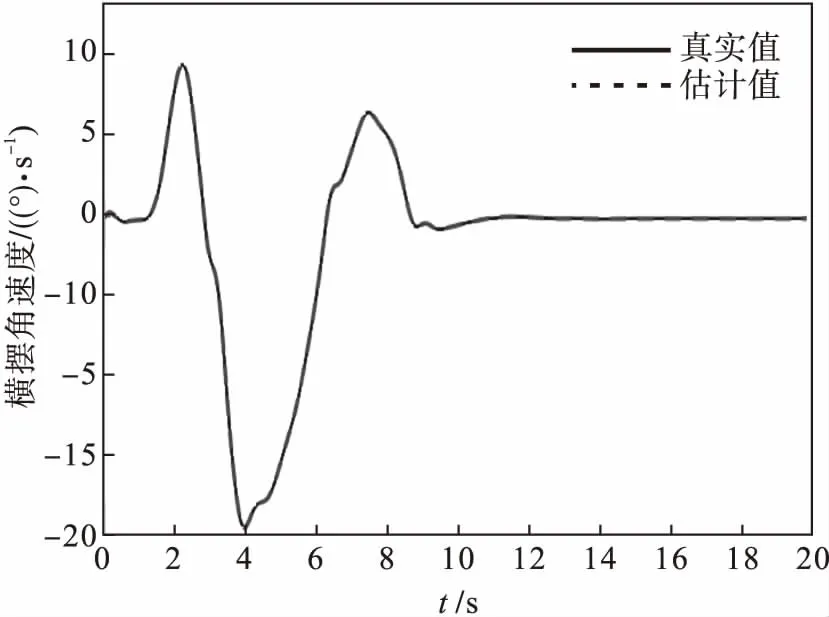
图8 横摆角速度变化曲线(μ=0.2)

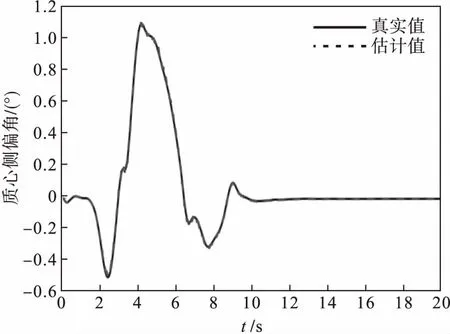
图9 质心侧偏角变化曲线(μ=0.2)

通过图10和图11可以看出,观测器在低附着路面能精确地估计横摆角速度和质心侧偏角,并且能够检测出执行器故障.其中横摆角速度的观测误差在0.025(°)/s以内,质心侧偏角的观测误差在0.04°以内,说明所设计的观测器具有较强的鲁棒性.由图8和图9可知,在冰雪路面运行的横摆角速度的幅值在-20～9.6(°)/s,质心侧偏角幅值在-0.5°～1.2°.由图3和图4可知,在湿滑路面行驶时,横摆角速度幅值为-8.7～4.7(°)/s,质心侧偏角幅值为-0.23°～0.32°,最终都稳定在0.低附着系数的路面横摆角速度和质心侧偏角都比高附着系数的曲线变化更明显,符合高附着系数路面有更高稳定性的特性.

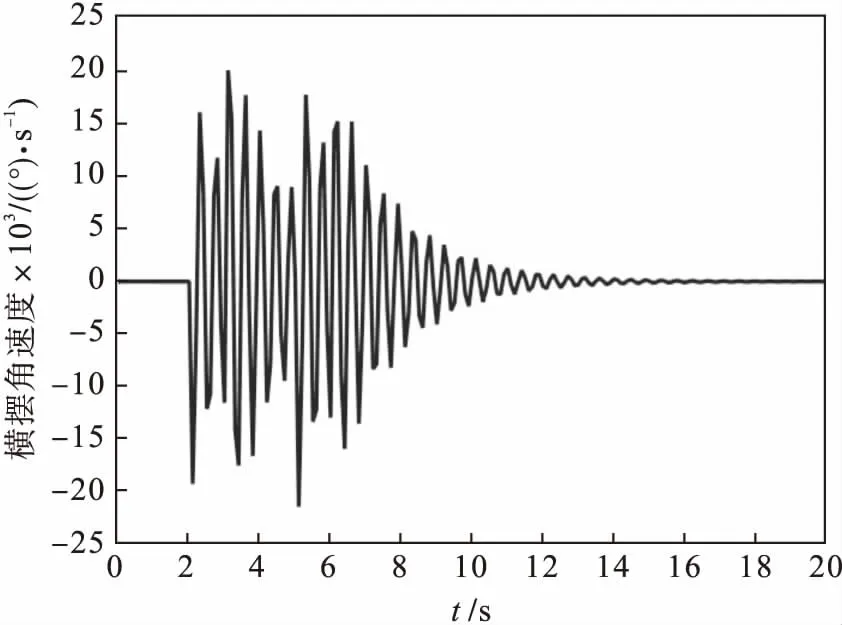
图10 横摆角速度误差曲线(μ=0.2)

图11 质心侧偏角误差曲线(μ=0.2)

图12和图13为在相同行驶条件下,附着系数0.2工况下四轮转向与前轮转向的横摆角速度

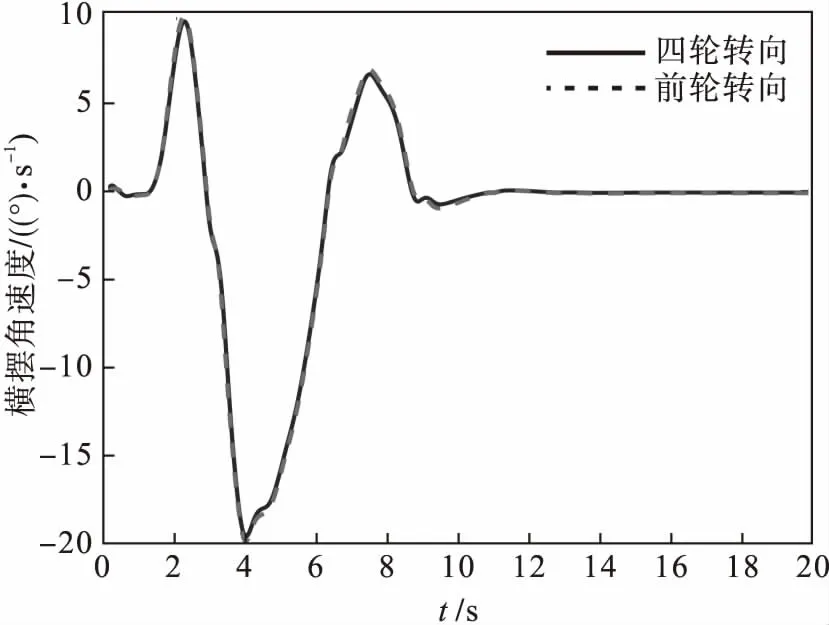
图12 横摆角速度响应曲线(μ=0.2)

和质心侧偏角对比曲线.对比图12和图13中2条曲线发现,高速运行时,采用四轮转向系统的横摆角速度和质心侧偏角幅值都减小,最后在零值附近达到稳定状态.图13中采用四轮转向系统到达稳定时间更短,说明四轮转向系统能够显著改善质心侧偏角,增强高速运行时车辆的稳定性.与前轮转向系统相比,采用四轮转向系统能提高车辆运行时的可靠性和乘坐的舒适度,更满足人们的需要.

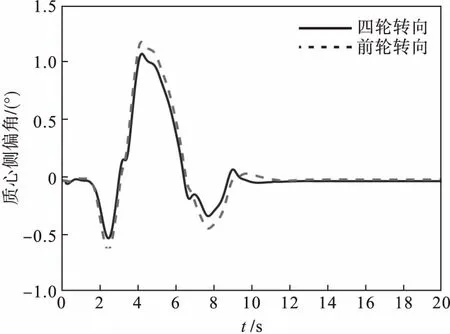
图13 质心侧偏角响应曲线(μ=0.2)

4 结 语

针对车辆ESC系统,建立双输入双输出四轮转向控制数学模型,设计观测器实现不确定ESC系统执行器故障检测,选取双移线工况进行仿真验证.结果表明:在不同工况下,观测器的观测效果良好,当执行器发生间歇故障时存在误差,但很快观测器的估计值能够跟踪上真实值.并且采用四轮转向控制比前轮转向控制横摆角速度和质心侧偏角波动更小,更接近于零,对车辆稳定性作用更明显,能有效避免车辆在高速低附着系数路面车辆发生侧滑及甩尾等.所设计的观测器能够进行故障诊断,且有较好的鲁棒性和实用性.