重载铁路路基粗粒土填料回弹特性试验研究
聂如松,孙宝莉,程龙虎,李亚峰,卢小永,李光耀
(1.中南大学 土木工程学院,湖南 长沙 410075;2.中南大学 重载铁路工程结构教育部重点实验室,湖南 长沙 410075;3.中铁第四勘察设计院集团有限公司,湖北 武汉 430063;4.大秦铁路股份有限公司,山西 太原 030013)
重载铁路货物输送能力大,经济和社会效益显著。发展铁路重载运输,已成为世界各国铁路运输发展的重要方向[1]。重载列车轴重大、编组长,行车速度相对较慢,重载列车产生的动荷载和作用时长较一般路基大,路基在重载列车荷载长期作用下的动力稳定性是业界关注的热点问题[2-4]。粗粒土填料因具有压实性能好、透水性强、抗剪强度高、地震荷载作用下不易发生液化等优良工程特性而广泛应用于铁路路基基床层。在重载列车荷载作用下,路基产生的变形既有不可恢复的累积塑性变形又有弹性变形,过大的弹性变形会对列车的安全运行构成威胁。回弹模量是表征轨下结构弹性变形特性的重要力学参数,是反映整个轮轨系统垂向动力特性的重要参数。轨道性能在很大程度上取决于道砟、底砟和路基层的弹性特性。道床和路基材料的回弹模量对于轮载作用下轨道和下部结构的分析和设计至关重要[5]。因此,研究列车动荷载作用下粗粒土填料的回弹特性对于重载铁路路基的设计和维护具有重要意义。
国内外学者对路基土回弹模量的影响因素如土体类型[6]、压实度[7-8]、基质吸力[9]、含水率[6-10]、应力状态[11]等进行研究并建立了回弹模量预估模型[11-19],然而这些研究大多是针对细粒土[6-12]开展的。重载铁路路基基床层多采用级配碎石或A组填料,多为粗粒土。已有部分学者开展了粗粒土的回弹特性研究。石章入等[20]利用动三轴仪,对公路土石混合路基填料开展了循环动荷载三轴试验,分析了应力水平、含水率、粗骨料岩性等因素对土石混合料回弹模量的影响。朱俊高等[21]以高土石坝为研究背景对不同级配的粗粒土填料开展了常规三轴固结排水剪切试验和卸载-再加载剪切试验,分析了粗粒土回弹模量取值规律。Duong等[22]通过大型循环三轴试验研究道砟与路基夹层土的回弹特性,分析了细粒含量、含水率不同情况下的粗粒土回弹模量的变化规律。Kumar等[23]通过三轴试验分别研究了公路路基粗粒土和细粒土填料回弹模量随应力状况、含水率等因素的变化规律。胡焕校等[24]以高速公路路基填料为研究对象,开展了动三轴试验,研究了粗粒土填料动力特性同时结合工业CT技术分析了其细观力学性能,并分析了荷载频率、含水率对填料回弹模量的影响。上述对粗粒土回弹模量的研究虽取得一定的成果,但多以土石坝堆料或公路路基粗粒土填料为研究对象,而土石坝区别于铁路路基,它未承受像列车动荷载作用,故多采用静荷载对其进行研究。铁路路基所受的动荷载大于公路路基,动荷载波形和持续时间也不同,故填料回弹特性存在差异。综上,对于广泛用于铁路路基填筑的粗粒土填料在持续列车循环荷载作用下的回弹特性研究并不多,且对于粗粒土回弹模量的影响因素研究较为局限。因此,开展列车荷载作用下粗粒土填料回弹特性及其影响因素研究,具有重要的理论和实用价值。
本文以粗粒土填料为研究对象,开展持续振动条件下的大型动三轴试验。研究不同动应力幅值、循环振次、围压、含水率对粗粒土回弹特性的影响,为回弹模量取值及重载铁路路基基床层状态评估和养维提供参考。
1 动三轴试验
1.1 试验土样及其制备
试验所用土样由圆砾、河砂、低液限粉土组成。细圆砾石与河砂均取自湘江长沙段,低液限粉土取自朔黄铁路路基。通过室内试验得到低液限粉土颗粒相对密度Gs=2.71,液限wL=26.0%,塑限wp=18.2%,最优含水率wopt=11.80%,最大干密度ρdmax=1.96 g/cm3(重型Z1击实仪击实试验)。按照圆砾、河砂与低液限粉土质量比例为50∶50∶14.63的关系进行配比。配比后的粗粒土最大干密度ρdmax=2.21 g/cm3,最优含水率wop=6.0%,饱和含水率wsat=9.3%,颗粒相对密度Gs=2.68。其颗粒级配曲线见图1。根据TB 10001—2016《铁路路基设计规范》[25],试验土样为良好级配含土细圆砾,为A2组填料,满足TB 10625—2017《重载铁路设计规范》[26]对重载铁路路基基床表层和底层的填料要求。

图1 颗粒级配曲线
试验土样按压实度K=0.97控制制样,制样过程严格依据TB 10102—2010《铁路工程土工试验规程》[27]的规定进行。试样直径30 cm,高60 cm。为保证试样土颗粒上下均匀分布,分为6层压实,层高均为10 cm。当击实到指定高度时,停止击实,刮毛后放入下一层土料,然后再击实。如此循环至土样完成。到试样帽上,再在其外同样套上三层橡皮筋,箍紧。上述工作做完后,卸走两瓣式对开模,试样制做完成。最后,用空心软管连接试样帽和压力室底座接头,以便于试样能进行饱和、固结和施加反压。对于饱和试样,采用抽气使其达到真空状态(约2 h),再用水头饱和法进行饱和。
1.2 试验仪器
目前国内大型动三轴仪很难满足长时间重复加载的试验要求,本课题组通过对已有的大型静三轴仪(SZ304)进行改进,使其满足高振次、低围压的工作要求。压力室利用静三轴的压力室,动力荷载作用采用MTS加载系统施加。MTS加载系统稳定性好、控制精度高,可以施加高循环振次的动载。围压采用静水压施加,由于路基填料所受围压小,采用静水头控制其水压的大小。试样的轴向位移由MTS加载系统自动记录。
1.3 试验方法
试验采用正弦波来模拟列车动荷载,已有研究表明[27],对路基影响最大的频率为车辆的通过频率[5],即路基所受列车荷载的主频f=V/L(V为列车运行速度,L为车辆长度)。朔黄铁路重载列车运行速度为50~80 km/h,主要车型C70和C80的长度为13.976 m,故重载列车对路基的动力作用的主频为0.99~1.59 Hz,考虑频率的变化范围较小,为取值方便,试验的加载频率取1 Hz。朔黄重载铁路基床层厚度为2.5 m,基床表层厚度为0.6 m,基床底层厚度为1.9 m。朔黄铁路目前开行轴重25 t的列车和2万t列车。文献[28]进行的路基应力实测表明,路基基床的围压范围为25~60 kPa,所以试验围压取15、30、45、60 kPa。李子春[29]通过实测数据,发现轴重为19.6~22.5 t的列车对路基面产生的最大动应力位于35~185 kPa之间。梅慧浩等[30]依据朔黄重载铁路建立三维有限元模型,分析列车轴重为25、27、30、35 t时路基面动应力峰值分布特征,并预测了轴重25~30 t时路基面最大动应力峰值为91~123 kPa。考虑到重载铁路列车荷载比普通铁路大很多,同时为了分析粗粒土的动强度和临界动应力,试验中有意扩大了加载动应力幅值,动应力幅值见表1。

表1 粗粒土大型动三轴试验方案
试验中考虑了填料3种含水率状态,最优含水率(wop=6.0%)、饱和含水率(wsat=9.3%)和处于最优含水率和饱和含水之间的自然状态(w=7.5%)。加载方式见图2。图2中,σ3为固结阶段的围压值,σs为上部结构(道砟、轨枕和轨道等)对路基的静载作用,取值为15 kPa[31],σd为动应力幅值。试验过程采用固结不排水方式,固结比为1.0。

图2 试验加载方式
试验中,对于破坏试样,采用轴向应变达到15%作为其破坏标准。若试样轴向应变的增量在2 h内始终小于1 mm,则认为试样达到动力稳定状态,不发生破坏,加载振次达到50 000次停止试验。
2 试验结果分析
2.1 应力-应变关系曲线分析
试样的动应力-动应变关系曲线,见图3。试样在一个周期的动荷载作用下的动应力与动应变呈一个滞回圈。在循环动荷载作用下,试样的动应力与动应变的关系曲线由许多滞回圈组成。滞回圈随着循环次数的增加逐渐水平右移,表明试样在动荷载作用下同时产生了塑性和弹性应变。根据累积塑性应变随着循环振次的发展趋势,通常可以将试样在动荷载作用下的状态分为三类:稳定型、破坏型和临界型。
由图3(a)可知,随着循环振次的增加,滞回圈一直右移,反映了累积塑性应变逐渐增加,当累积塑性应变达到0.6%时,滞回圈逐渐趋于重合,累积塑性应变增长缓慢甚至停止增长,表明试样处于稳定状态。
由图3(b)可知,滞回圈随着振次的增加一直水平右移,表明试样累积塑性应变一直处于不断增长状态,直到试样轴向累积塑性应变达到15%,试样破坏。
由图3(c)可知,滞回圈随振次的变化规律介于图3(a)和图3(b)之间。在加载初期,累积塑性应变随循环振次的增加而快速增长,滞回圈相应地向右移动,随着累积应变增长速率逐渐减小,滞回圈向右移动的速率也相应地降低,但未出现图3(a)中滞回圈重合的现象,反映了塑性应变仍处于不断增长状态。

图3 动应力-动应变关系曲线
当土体在动荷载作用下不考虑塑性应变的影响,可把土体视为黏弹性体。黏弹性体滞回圈示意图和试样实测滞回圈见图4。在一个动荷载作用周期内,滞回曲线以坐标原点为中心、封闭而且上下基本对称,滞回圈的形状和大小不受振次的影响,该滞回曲线反映了动应变对动应力的滞后性,见图图4(a)。实际上,土为黏弹塑性体,在动荷载作用下土中塑性变形的出现将使滞回曲线不再封闭、对称,滞回曲线整体将随着振次的增加向累积应变增大的方向移动,反映应变逐渐累积的特性,见图4(b)。

图4 黏弹性体滞回曲线示意图和试样实测滞回圈
2.2 累积塑性应变随振次的关系
以饱和粗粒土样在围压σ3=15、30、60 kPa、ω=9.3%时的累积应变ε与振动次数N关系曲线为例来说明累积塑性应变随振次的发展关系,见图5。

图5 ε-N关系曲线
由图5可知,动应力幅值大小对土体的累积应变发展规律有显著影响。当σd≤100 kPa时,不同围压下的试样均处于稳定状态。其中σd=50 kPa时,围压σ3=15、30、60 kPa累积应变分别为0.34×10-2、0.17×10-2、0.02×10-2;σd=100 kPa时,围压σ3=15、30、60 kPa时累积应变分别为3.3×10-2、0.69×10-2、0.24×10-2。当动应力幅值σd=125 kPa时,试样累积应变随围压表现出不同的发展规律,围压σ3=15、30 kPa时土体因累积变形超过破坏标准发生破坏,围压σ3=60 kPa时土体在开始阶段累积变形增加较快,振动次数约30 000次时达到动力稳定,没有发生破坏。当动应力σd≥150 kPa时,粗粒土样累积应变随着振动次数的增加而增加,最终都达到破坏。从试样的累积塑性应变与振动次数N的关系曲线也可以将试样在动荷载作用下的类型分为稳定型、破坏型和临界型。
2.3 回弹模量的确定
回弹模量是表征填料回弹特性的重要参数。回弹模量为
(1)
式中:MR为回弹模量;σdmax、σdmin分别为每个循环振次的最大动应力与最小动应力;εrmax、εrmin分别为每个循环振次的最大动应变与最小动应变。
回弹模量的几何意义为应力-应变关系图中滞回圈两端点连线的斜率。根据动应力-应变关系曲线确定回弹模量的示意,见图6。由图6可知,加载初期,滞回圈非闭合,很难从单独一个滞回圈中确定土体的回弹模量。因此,在加载初期,本文采用相邻两个滞回圈确定土体回弹模量的方法[32],两个循环振次的滞回圈存在两个交点并由此构成了一个新的闭合滞回圈,可根据该闭合滞回圈来进行回弹模量的确定(图中蓝色直线的斜率即为回弹模量)。随着循环振次的增大,滞回圈呈闭合状态,回弹模量通过最低点和最高点之间连线的斜率求得。
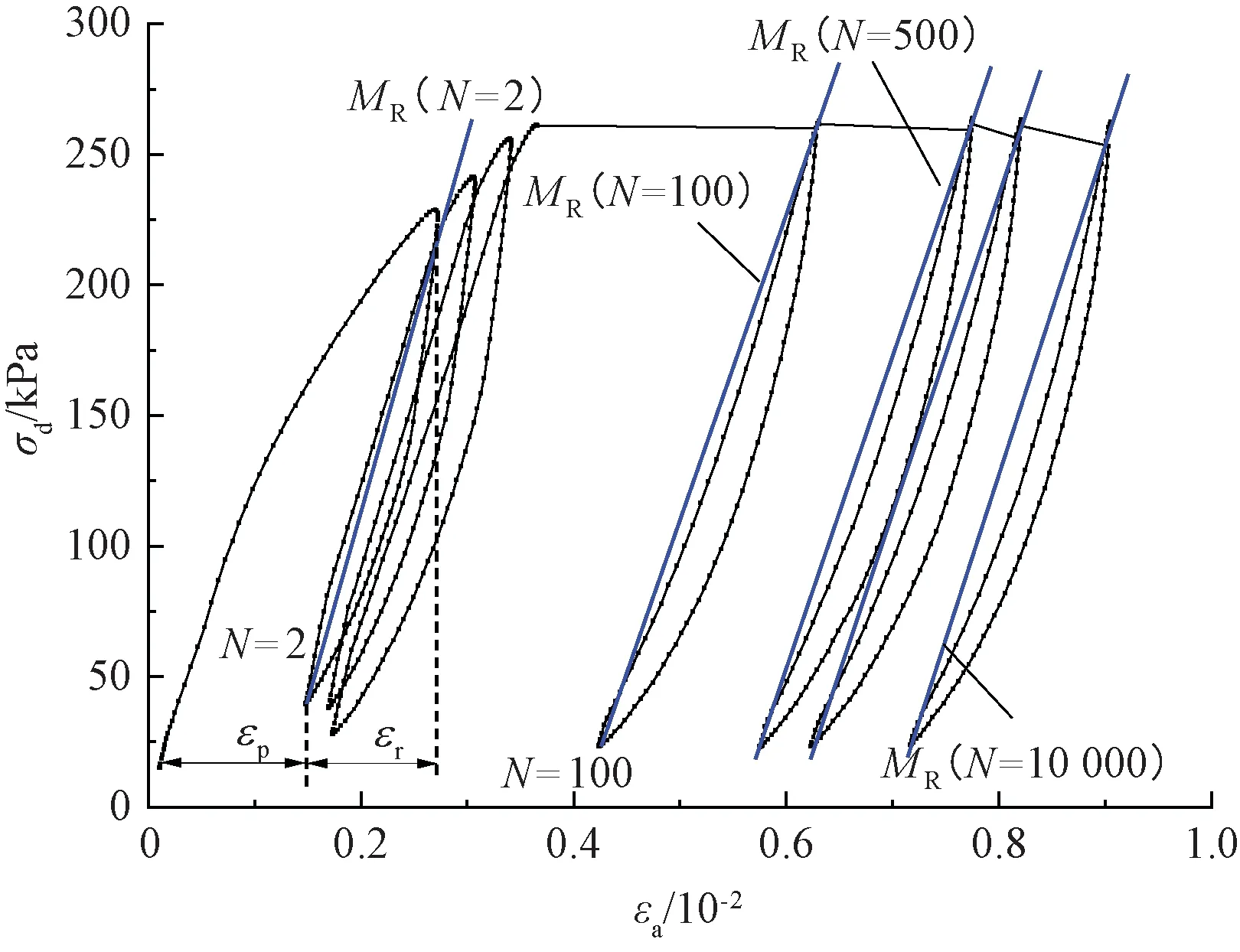
图6 回弹模量的计算
2.4 回弹模量随振次的变化规律
饱和与非饱和状态粗粒土的回弹模量MR与循环振次N的关系曲线,见图7、图8。由图7和图8可知,在不同的物理状态和应力条件下,粗粒土的回弹模量在加载初期均具有较大的波动性,加载初期几圈内粗粒土回弹模量迅速下降,随着循环振次的增加,这种迅速下降的趋势很快结束。这是由于重塑试样在初始剪切阶段经压实形成的结构发生一定的扰动,土体刚度发生一定的衰减,因此初始时试样的回弹模量迅速下降;随着循环振次的增加,试样中颗粒重新排列形成新的结构,在循环荷载作用下土体逐渐密实,回弹模量缓慢增加。Lunne等[33]的研究也发现类似的规律。

图7 不同动应力条件下饱和粗粒土MR-N关系曲线
随着循环振次的逐渐增加(N>10),饱和与非饱和试样的回弹模量随循环振次发展规律具有明显的不同。由图7可知,对于饱和稳定试样(w=9.3%),回弹模量表现为缓慢增加并逐渐趋于稳定的变化规律,不同应力状态下饱和试样的回弹模量基本在1 000振次后达到稳定微增长状态。个别试样在较高动荷载下作用一定振次后遭到破坏,回弹模量随振次逐渐下降直至试样破坏,如图7(c)中动荷载σd=150 kPa时试样在循环约1 000次后回弹模量迅速降低直至试样破坏。其产生的主要原因可能有以下2个方面:①动应力幅值较大;②试样尺寸大,试样制作过程中,试样的均匀性和一致性控制难度大,试样的局部不均匀对试验结果会产生影响。由图8可知,对于非饱和稳定试样(w=6.0%、7.5%),回弹模量随循环振次的增加始终呈现出持续上升的发展趋势,即试样的刚度随循环振次的增加逐渐硬化。

图8 不同动应力条件下非饱和粗粒土MR-N关系曲线
2.5 回弹模量随动应力幅值的变化规律
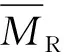
图9 不同工况下关系曲线
从图7和图8中还可以看出,重载铁路路基基床层的动应力处于91~123 kPa之间时[30],粗粒土回弹模量处于80~90 MPa之间。
2.6 回弹模量随含水率的变化规律
不同应力水平、含水率状态下回弹模量随循环振次变化的关系曲线,见图10。由图10知,随着含水率的增大,回弹模量呈下降趋势,这是由于路基粗粒土填料自身黏性较低,含水率的增大使得颗粒间摩擦力减小,骨架结构变得不稳定,从而引起土体回弹模量的降低。当应力水平较低时(σd=100 kPa,σ3=15 kPa),两种含水率情况下的回弹模量随循环振次的变化关系曲线在振动前期存在相交的现象,回弹模量值在80~83 MPa之间,相差不大;当应力水平较高时(σd=250 kPa,σ3=60 kPa),随着含水率的增大,回弹模量呈明显下降趋势。

图10 不同应力和含水率条件下粗粒土MR-N关系曲线

表2 不同应力水平和含水率条件下粗粒土回弹模量值
由表2可知,当围压为15 kPa、动应力为100 kPa时,含水率由6.0%升至9.3%,回弹模量值约下降3.99%。当围压为60 kPa、动应力为250 kPa时,含水率由6.0%升至9.3%,回弹模量值约下降17.42%。由此可知,随着粗粒土填料所受应力水平的提高,含水率的变化对路基回弹模量的影响越来越显著。压实粗粒土随着细粒土含量的变化可以分为悬浮密实结构、骨架密实结构和骨架孔隙结构三种土体结构类型[35]。压实粗粒土结构类型不同,表现出来的工程特性也有很大差异,悬浮密实结构以细粒土土为主导,其工程特性主要由细颗粒主导。本文所研究的粗粒土细颗粒含量约为14%,粗颗粒为卵石土,在含水率增加情况下,其含水率主要由细颗粒所持有,导致水和细粒土在卵石颗粒之间起到润滑作用,同时含水率增加使土颗粒结合水膜增厚,黏聚力降低,其抗剪强度也随之降低,特别地,围压为150 kPa时该粗粒土的抗剪强度比围压为100 kPa时降幅大[36]。在实际工程中,受降雨的影响,路基土含水率往往大于填筑时的最优含水率,因此在设计过程中,应适当考虑因含水率的增大引起的回弹模量的折减,以提高路基设计水平。
2.7 回弹模量随围压的变化规律

图11 不同工况下粗粒土关系曲线
3 结论
通过开展循环荷载作用下大型动三轴试验,研究重载铁路路基粗粒土填料在不同循环振次、应力水平、含水率条件下的回弹特性,得到如下结论:
(1)粗粒土的回弹模量在加载初期均具有较大的波动性,加载初期回弹模量迅速下降,随着循环振次的增加,回弹模量逐渐增加。饱和粗粒土的回弹模量在循环振次大于1 000后趋于稳定微增长状态;非饱和粗粒土回弹模量随循环振次的增加呈现出持续增长状态。
(2)动应力幅值与围压均对粗粒土回弹模量有较大的影响,但动应力幅值的影响更为显著。回弹模量随着动应力幅值与围压的增大而增大。重载铁路路基基床层动应力在91~123 kPa范围时,粗粒土基床层回弹模量为80~90 MPa。
(3)粗粒土填料回弹模量随着含水率的增大而降低。当围压和动应力幅值较大时,含水率从最优升至饱和状态,回弹模量值下降较明显,即粗粒土回弹模量“水敏感性”受应力水平的影响显著。

