基于证据推理的改进加权CREAM模型

孙延浩，张 涛，刘宁馨，李 伟

(1.中国铁道科学研究院集团有限公司通信信号研究所，北京 100081；2.国家铁路智能运输系统工程技术研究中心，北京 100081；3.中国铁道科学研究院集团有限公司运输及经济研究所，北京 100081；4.北京市华铁信息技术有限公司，北京 100081)

人因可靠性是用来描述人的绩效的术语，它是指在规定的时间和条件下，参与人无差错地完成规定任务的能力[1]。为了更好地对人因可靠性展开科学性、系统性的研究，人因可靠性分析(Human Reliability Analysis,HRA)技术应运而生，自20世纪90年代以来，随着认知科学的发展，HRA技术得到了极大的发展，涌现了一批新的HRA方法，其中最为典型的就是Hollnagel博士于1998年提出的认知可靠性与失误分析方法(Cognitive Reliability and Error Analysis Method，CREAM)[2]。该方法由于具有可操作性和通用性强等特点，已被广泛应用于核电业、远洋运输业、航空运输业和近海石油钻探等人因安全性和可靠性要求较高的领域。

CREAM强调人在生产活动中的绩效输出不是孤立的随机性行为，而是通过人完成任务时所处的情景环境即共同绩效条件(Common Performance Condition，CPC)来影响人的认知控制模式，并最终决定人的响应行为。CREAM分为基本法和扩展法。基本法较为简单，但无法获得相对精确的人因失误概率(Human Error Probability,HEP)，因此不少学者致力于在基本法的基础上获取HEP的点值计算。如Ung[3]在获取CREAM的控制模式后通过IF-THEN规则计算HEP；Marseguerra等[4]和Yang等[5]通过运用模糊推理方法建立了基于CREAM的模糊推理模型，实现了HEP的定量计算。为了降低CPC绩效评价的主观性，已有研究[6-7]将多属性决策方法引入到CREAM中。此外，贝叶斯网络(Bayesian Network，BN)也被运用到CREAM中，如一些学者[8-10]利用BN来获取控制模式的概率分布，并在此基础上得出HEP的点值。还有一些学者在扩展法的基础上对CREAM进行了改进。如Chen等[11]采用网络分析法(Analytic Network Process，ANP)对CPC间的相关性进行了分析，并确定了CPC的权重；裴立冠等[12]利用模糊理论对扩展法进行了改进;高扬等[13]通过不确定分布来修正CREAM扩展法中人的常模基本失误概率，并以此来分析飞行员应急操作的可靠性。但2012年CREAM的创始人Hollnagel博士在其个人博客中发表了一则针对CREAM扩展法的免责声明，指出CREAM扩展法存在着一些不可避免的缺陷。故本文只对CREAM基本法进行改进，文中CREAM也特指其基本法。

虽然改进的CREAM在应用方面取得了一些成果，但现有的改进CREAM在指标权重的计算和数据的聚合计算方面依然存在着不足，这使得HEP的计算精确度不高。为了解决此问题，本文提出一种基于证据推理(Evidential Reasoning,ER)的改进CREAM模型。该模型首先通过决策实验室分析(Decision Making Trial and Evaluation Laboratory,DEMATEL)法和模糊层次分析法分别来计算CPC的相关性权重和重要性权重；然后利用组合赋权法将相关性权重和重要性权重进行线性组合，获得CPC的综合权重，在此基础上利用ER算法对CPC的绩效效应进行加权数据融合，并利用融合后的数据获取情景影响指数(Context Influence Index,CII)，通过CII实现了HEP的点值输出；最后将该改进的CREAM模型运用到高速铁路列车调度员的人因可靠性定量评估案例中，验证模型的可行性和有效性。

1 基本方法

1.1 认知可靠性与失误分析方法(CREAM)

CREAM将操作人员克服或者适应情景环境所必需的能力或者付出的努力称为控制模式，并根据情景环境的不同，将控制模式分为4种，分别为混乱模式、机会模式、战术模式和战略模式。同时，CREAM也给出了这4种不同控制模式下的HEP区间，见表1。

表1 不同控制模式下的HEP区间Table 1 HEP interval of different control modes

CREAM将情景环境归纳为9种CPC，分别是组织的完善性C1、工作条件C2、人机界面与运行支持的完善性C3、规程/计划的可用性C4、同时出现的目标数量C5、可用时间C6、值班时间C7、培训与经验的充分性C8和班组成员的合作C9。每个CPC又分为不同的层次，根据其对人因可靠性的绩效效应分为正效应的“改进”、中性效应的“不显著”和负效应的“降低”3种情况。通过统计正、负绩效效应的数量，根据图1运用坐标方式(∑降低，∑改进)来确定控制模式，再通过表1来确定HEP区间。

图1 CREAM控制模式定义图Fig.1 Definition Diagram of CREAM Control Mode

CREAM虽然计算简单，但却存在着明显的不足，首先是HEP区间有重叠、且宽泛，这将导致其预测精度不高；其次是认为CPC对人的绩效影响相同，但在实际中不同的CPC对人的绩效影响并不相同，即不同的CPC的权重是有差异的；最后CREAM通过将情景环境离散化来确定控制模式，这种确定方式稍显粗糙，控制模式应表示为连续定量函数[17]。为此，不少学者致力于CREAM的改进，本文在既有学者研究的基础上，将对CREAM再次进行了相应的改进。

1.2 证据推理(ER)算法

证据推理算法又称ER算法，是一种基于Dempster-Shafe证据理论和决策理论的多源信息融合算法[14-15]。相较于其他算法，ER算法对于一些模糊不确定、概率不确定以及非线性特征的数据具有很强的建模能力，从而使得数据融合的结果更加可信。其基本理论如下：

S(yi)={(hj,βj,i),j=1,2,…,n}

(1)

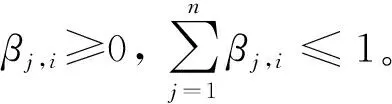
令mj,i表示二级指标yi支持一级指标X被评为hj的程度，mH,i表示一级指标X被评为“不确定”的程度(不在任何评语集中),则：

(2)

(3)

将l个二级指标yi聚合后支持一级指标X被评为hj的程度表示为mj,I(i)，mH,I(i)表示l个二级指标yi聚合后支持一级指标X被评为“不确定”的程度。

mj,I(i+1)=KI(i+1)[mj,I(i)mj,i+1+mH,I(i)mj,i+1+mj,I(i)mH,i+1]

(4)

(5)

(6)

(7)

(i=1,2,…,l-1)

(8)

式中：I(i+1)表示聚合成i+1个二级指标；KI(i+1)为冲突因子，表示不同指标支持某一评价等级的程度。

计算一级指标X的聚合信任度，其公式如下：

(9)

(10)

式中：βj表示一级指标X的评价等级为hj的信任度;βH表示一级指标X的评价等级为“不确定”的信任度。

根据公式(9)和(10)，可以得到一级指标X的评价分布为

S(X)={(h1,β1),(h2,β2),…,(hn,βn),(hH,βH)}

(11)

由于CPC的绩效效应分为“改进”、“不显著”和“降低”，因此CPC的绩效效应对应的等级隶属度分布可表示为

S(CPC)={(h1,β1),(h2,β2),(h3,β3)}

(12)

式中：h1、h2和h3分别对应于“改进”、“不显著”和“降低”3种绩效效应的等级;β1、β2和β3分别为3种绩效效应等级对应的隶属度。

2 基于ER的改进CREAM模型

2.1 CPC权重的确定

2.1.1 CPC的相关性权重计算

CPC是影响CREAM控制模式的重要因子，Hollnagel[2]研究认为CPC间存在着一定的关联性，并在研究了大量人因事故之后给出了CPC的调整规则，见表2。

表2 CPC的调整规则[2]Table 2 Rules for adjusting the CPC[2]

本文以C2为例，对CPC的调整规则进行说明。若C2的绩效效应为“不显著”，那么在C1、C3、C6、C7和C8这5个CPC中有4个及4个以上CPC的绩效效应为“改进”，那么C2的绩效效应由“不显著”调整为“改进”；当上述5个CPC中有4个及4个以上CPC的绩效效应为“降低”时，那么C2的绩效效应由“不显著”调整为“降低”。另外3个CPC的调整规则与之类似，在此不作赘述。

对于CPC的权重计算，大部分CREAM的改进模型采用的是层次分析(AHP)法，但AHP法无法考量CPC之间还存在着一定的相关性。从信息论的角度可知，若某个CPC与其他CPC的相关性越小，那么它所提供的信息的区分度越高，信息量也越大，则该CPC越重要，其赋予的权重也应越大。可见，根据CPC之间的关联性进行权重的分配是合理的。

决策实验分析方法是一种分析要素间相关关系的重要方法[16]。考虑到CPC之间的相关性，因此本文采取DEMATEL法来计算CPC之间的相关性权重，具体计算步骤如下：

(1) 将CPC之间的关系用0～5标度来表示，0表示无影响，1表示影响弱，2表示影响比较弱，3表示影响一般，4表示影响较强，5表示影响很强。构建CPC之间的直接影响矩阵Zk：

(i=1,2,…,m;j=1,2,…,n)

(13)

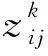
(2) 规范化直接影响矩阵Zk，得到规范矩阵Ak:

(14)

(3) 计算CPC之间的综合影响矩阵Tk：

(15)

式中:I为单位矩阵。

(16)

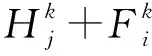
(17)

式中：λk为第k个专家的权重。

2.1.2 CPC的重要性权重计算

在实际中由于不同的CPC对人的绩效效应的影响不同，因此其本身的重要性也要考虑，即需要对其本身的重要性权重进行分配。AHP法是一种常用的赋权方法，但在使用的过程中，若待测评指标较多时，其判断矩阵的一致性与人类的思维一致性存在着一定的差异，同时该方法的主观性较强。为了使重要性权重的计算更加准确，本文采用基于模糊一致性矩阵的模糊层次分析法来计算重要性权重，其计算步骤如下：

(1) 利用0.1～0.9标度(见表3)，构建重要性判断矩阵Bk:

表3 0.1～0.9标度及其含义Table 3 0.1 ～ 0.9 scale and its meaning

(18)

(2) 将重要性判断矩阵转化为模糊一致性矩阵Rk，再将其进行加权集结，得到综合模糊一致性矩阵R：

(19)

(20)

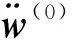
2.1.3 CPC的综合权重计算

为了得到更加准确的CPC权重，将上述两种方法求得的CPC权重通过组合赋权法进行线性组合，并引入调节参数ρ，得到综合权重W的计算公式如下：

(21)

式中:W=(w1,w2,…,wn)；ρ为参数,为不失一般性，取值为0.5。

2.2 HEP的计算

针对CREAM存在的离散问题，有3条已被证实的合理性前提假定[17-18]：

(1) 控制模式和HEP均为连续的；

(2) HEP随着CPC的变化呈指数变化；

(3) 如果(∑改进，∑降低)=(7，0)，表示任务处于的情景环境处在最佳状态，HEP此时取得最小值；相反，若(∑改进，∑降低)=(0，9)，表示任务处于的情景环境处在最差状态，HEP此时取得最大值;如果(∑改进，∑降低)=(0，0)，表示情景环境对人没有影响，即无情景环境的影响，此时的认知失效概率称为基本失效概率。

HEP=HEP0exp(α×CII)

(22)

式中：HEP0为基本失效概率;α为待定常量。

由上述假定(3)可知：

(23)

其中，HEPmax=1.0，HEPmin=0.000 05(见表1)，将两者代入到公式(23)中，可计算得：

(24)

因此，人因失误概率HEP计算公式为

HEP=7.07×10-3exp(-4.951 7×CII)

(25)

借鉴Sun等[18]的CII计算公式，本文将CII定义为β1-β3，h1和h3分别为“改进”和“降低”的隶属度。CII中并没有考虑中性效应“不显著”，因为不管是在传统的CREAM中还是在改进的CREAM中，“不显著”的绩效效应值都为零，虽然有研究认为中性效应应该等同地分配给正负绩效效应[3]，即使采用这种观点，CII的结果依然不会改变[19]。

综上所述，本文构建了基于ER算法的改进CREAM模型总体流程，见图2。

图2 基于ER算法的改进CREAM模型流程图Fig.2 Flow chart of the improved CREAM model based on ER algorithm

3 案例应用与分析

3.1 案例描述

高速铁路列车调度指挥系统作为铁路运输系统的神经中枢，在保证高速列车的安全、正点和高效运输方面起着至关重要的作用[20]。高速铁路列车调度指挥系统是一个由人、设备、环境、信息4要素构成的复杂系统，其中高铁列车调度人员作为一个有着独立思维的系统要素，在协调和控制调度指挥系统方面起着主导作用。因此，有必要对其展开人因可靠性研究。

2021年5月27日，某高速铁路干线由于受到大风天气的影响，某路局调度台的列车调度员需要设置临时限速，为了评估列车调度员的可靠性，以调度员设置临时限速任务为例，某路局邀请4名专家D1、D2、D3和D4对列车调度员的操作进行观测评判，专家的具体信息见表4。

表4 专家的具体信息Table 4 Specific information of experts

3.2 CPC权重的确定

以专家D1对列车调度员的评判为例，其给出的直接影响矩阵Z1和重要性判断矩阵B1如下：

根据DEMATEL法和模糊层次分析法分别计算得到CPC的相关性权重和重要性权重，再通过组合赋权法得到CPC的综合权重，见表5。

表5 CPC的综合权重Table 5 Comprehensive weight of CPC

3.3 HEP的计算

4名专家根据当时观测到列车调度员操作情况，参考运输调度规则[21]和工作指南[22]，给出了列车调度员的CPC绩效效应评价信息，见表6。

表6 列车调度员的CPC绩效效应评价信息Table 5 Train dispatchers’information of CPC performanceeffect evaluation

首先，根据ER算法将4名专家给出的CPC绩效效应评价信息进行数据融合，得到CPC的绩效效应评价隶属度，见表7。

表7 CPC的绩效效应评价隶属度Table 7 Confidence of CPC Performance effect evaluation

然后，利用ER算法对9种CPC进行数据融合，得到CPC的综合绩效效应评价隶属度，见表8。

表8 CPC的综合绩效效应评价隶属度Table 8 Membership degree of CPC comprehensive performance effect evaluation

由表8可知，(∑降低，∑改进)=(0.147 1,0.287 8)，对应的认知行为控制模式为战术型。通过计算CII，可以得到CII=0.287 8-0.147 1=0.140 7。

最后，根据公式(25)，可计算得到HEP为

HEP=7.07×10-3exp(-4.951 7×0.140 7)

=3.522×10-3

3.4 模型的验证

由传统的CREAM模型可知，当(∑降低，∑改进)=(0.147 1,0.287 8)时，其控制模式为战术型，HEP值落在区间(0.001，0.1)内，而由改进的CREAM模型计算得出的HEP值为3.522×10-3，也在该区间内，从侧面验证了本文改进CREAM模型的有效性；但传统的CREAM模型只能得到HEP粗略的区间值，而改进的CREAM模型计算得出的HEP是相对精确的点值。将表5中9种CPC的绩效效应代入到相关文献[3]的方法中，计算得出的HEP值为3.467×10-3，都在战术型的HEP值区间(0.001，0.1)内。虽然两者计算结果有所差异，且本文改进CREAM模型的计算结果相对来说有点保守，但对于高速铁路列车调度指挥系统这种安全性要求高的系统来说是完全可以接受的，验证了将改进的CREAM模型运用到列车调度员的人因可靠性定量计算是可行的。

4 结论与建议

(1) CREAM是一种常用的HRA方法，但在CREAM的使用过程中，却存在着一些不足，为了弥补该方法在使用过程中的不足,本文提出了一种基于ER算法改进的CREAM模型，该模型可以实现HEP点值的连续输出。

(2) 考虑到CPC之间的相关性，利用DEMATEL方法获取CPC的相关性权重，并将其与CPC的重要性权重进行组合赋权，得到CPC的综合权重，从而使CPC权重的计算更加科学。

(3) 通过ER算法对CPC的绩效效应评价隶属度进行数据融合，得到CPC综合绩效效应评价隶属度，并依此进行CII的计算。

(4) 将改进的CREAM模型运用到高速铁路列车调度员的人因可靠性定量评估中，并通过与其他方法的对比分析，验证了该模型的有效性和可行性。

(5) 对于本文提出的改进CREAM模型来说，CPC的绩效效应评价主要依赖于专家或者专业人员现场的观测和经验，未来还需要优化CPC绩效效应的评价方法，而针对特定任务动态情境下的人因可靠性仿真将是下一步研究的重点。