控制翼前缘缝隙对层流分离的影响

陈 政，杨 瑜，何小龙，倪招勇，王军旗

(1 中国运载火箭技术研究院，北京 100076；2 中国航天空气动力技术研究院，北京 100074)

0 引言

作为世界各国争相研究的热点，高超声速飞行器一般为高升阻比、面对称气动布局，多利用控制翼(Flap舵、体襟翼)进行姿态控制。控制翼作为活动部件，为便于偏转，与机体间存在一定缝隙余量。工程中常在缝隙间填充弹性密封圈密封，但要实现完全密封技术难度很大。当飞行器再入通过大气层时，剧烈的气动加热和高温烧蚀，也可能因密封圈失效变形以及飞行器物面脱落等而出现缝隙。

图1 X-38飞行器控制翼前缘缝隙

此类飞行器在临近空间中高层高马赫数长时间持续飞行，由于单位雷诺数低，表面绕流一般处于层流状态，此时控制翼偏转等凸起部件诱导产生层流分离等复杂流动。一般情况下，控制翼前缘与飞行器后体具有较大压差，缝隙的存在，直接导致控制翼前缘和飞行器后体连通，在控制翼前缘形成抽吸作用，进而对控制翼诱导层流分离流动特性产生影响。

高超声速层流分离抗扰动能力弱，干扰范围广，由此形成的复杂流场将直接改变飞行器表面力/热分布，甚至影响飞行安全。针对高超声速飞行器控制翼诱导层流分离问题，结合工程实际,考虑前缘缝隙深入开展影响研究，对提升层流分离规律认识，指导飞行器结构设计具有重要的工程意义。以往研究多采用飞行器简化外形(带Flap舵的钝三角、平板/压缩拐角等)，且大多采用试验方法关注缝隙热流、抽吸流量等；而采用高精度数值方法获取流场精细结构，开展高超声速层流分离形态及范围影响研究相对较少。

基于此，为了获取前缘缝隙对控制翼诱导层流分离的影响，文中在控制翼前缘根部设计缝隙结构，通过数值模拟研究了不同缝隙宽度下控制翼诱导的层流分离形态，并在给定缝隙宽度下分析了不同舵偏角和攻角对控制翼诱导层流分离的影响规律。

1 数值方法与研究模型

1.1 数值方法

在曲线坐标系下，采用完全气体三维可压缩NS方程，其表达式为：

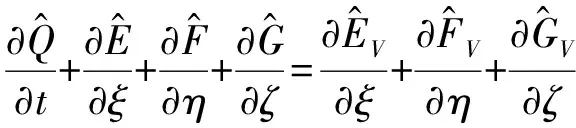
(1)

对控制方程无量纲化，采用有限体积法进行数值求解。根据以往研究经验，对流项采用Roe格式，单元界面左右变量重构选用Muscl格式和minmod限制器，粘性项采用中心差分格式，时间离散选择LU-SGS隐式方法推进。

针对类HTV-2高超声速飞行器控制翼无缝状态诱导的局部层流分离，在中国航天空气动力技术研究院高速风洞(FD-07)开展了相关实验研究工作。为了便于与无缝状态进行比较，文中数值模拟采用来流条件与风洞实验一致，即=8,=5 MPa,=750 K,无滑移等温壁=300 K。

1.2 模型及网格

基于HTV-2高速飞行器的外形，采用类HTV-2计算模型见图2，为了研究缝隙对控制翼诱导层流分离的影响规律，参考文献[8]在控制翼与机身之间设计如图3所示缝隙结构。

图2 类HTV-2高超声速飞行器外形

图3 控制翼前缘缝隙结构示意图

所设计的缝隙纵向剖面呈圆弧形，与控制翼面板半圆形前缘共轴，记前缘半径为，缝隙弧形半径为，缝隙宽度=-，其中=3.375 mm。前缘舵缝网格布置及全模网格拓扑结构如图4所示，半模网格量达1 500万。

图4 前缘舵缝网格布置及全模网格拓扑结构

高超声速层流分离数值模拟对网格质量要求高，特别是边界层、分离点等区域必须具有较高分辨率。鉴于文献[4]针对无缝状态数值模拟所得控制翼附近极限流线图谱和实验结果吻合较好(见图5)，认为其采用的网格满足此类流动的数值模拟需求，因此文中针对有缝状态网格与文献[4]保持一致。

图5 控制翼附近物面流动图谱(M∞=8.0，α=0°，δ=20° )[4]

2 计算结果及分析

2.1 缝隙宽度的影响分析

给定舵偏角=20°，以前缘半径为参考长度，依次模拟了为1.5，2.0,4.0,6.0和8.0五种不同缝隙宽度。

图6给出了不同缝隙宽度下控制翼附近局部极限流线图谱以及压力等值云图。对比极限流线，可以看出：分离范围随着缝隙距离的增大呈减小趋势，整个分离区逐渐向前缘中心缩进，分离范围越来越小，分离形态从瘦长的半椭圆形演变为近似半圆形。

随着缝隙宽度增大，抽吸增强，分离区积聚的流体从缝隙流向后体，分离区压力下降，分离前推受到抑制，分离距离减小；受飞行器前体影响，两侧流动向中间聚拢，在相同缝隙下，前缘中间位置抽吸流量不足以及时消除分离，分离依然存在，而两侧随着缝隙变大，分离受到抑制直至消失。

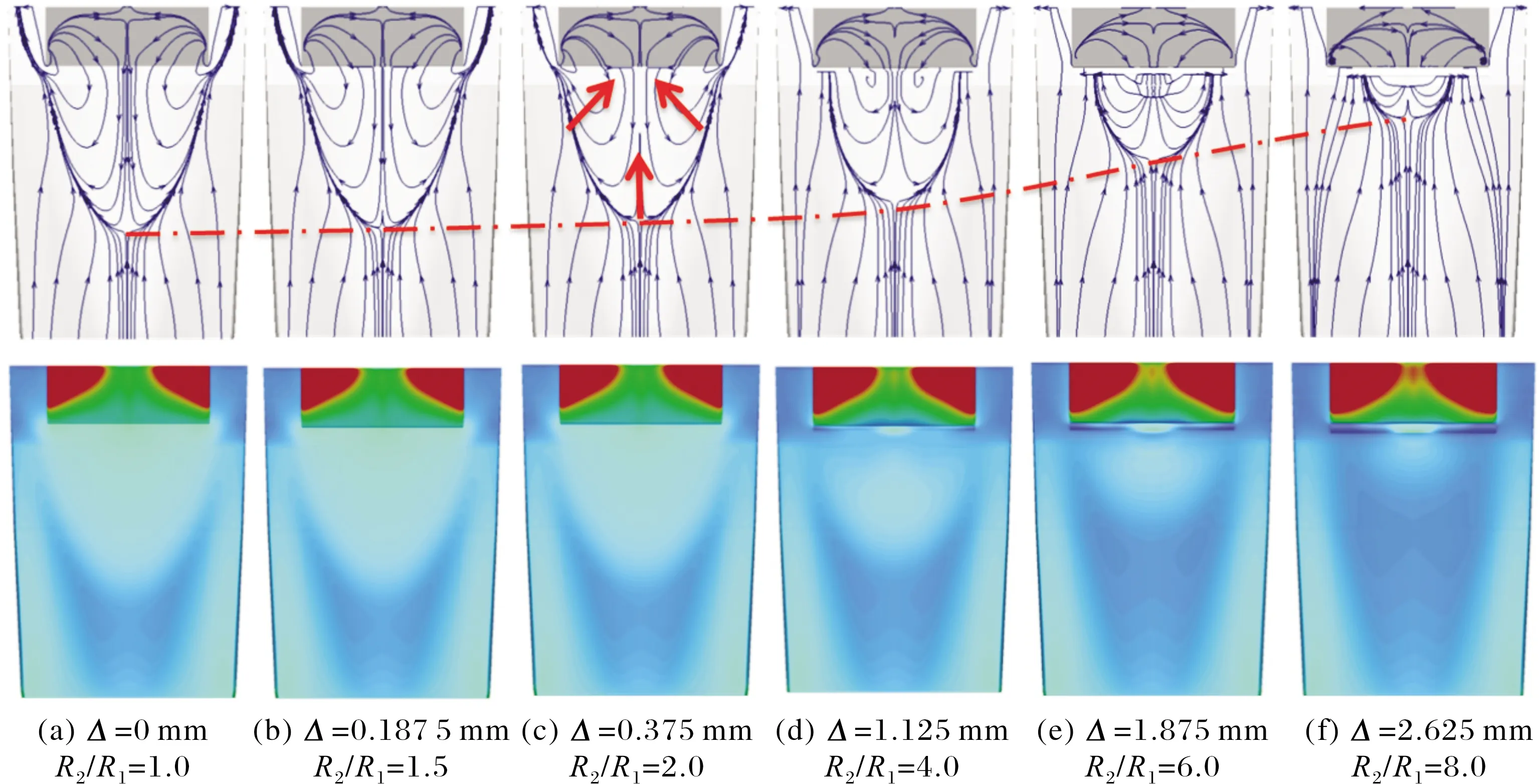
图6 不同缝隙宽度迎风面极限流谱及压力分布云图

通过积分获得各缝隙状态下控制翼诱导分离区面积，以无缝状态分离区面积作为参照值，得到分离区面积比，其随缝隙间距的变化规律如图7所示。由图可见，在较小缝隙下，由于抽吸流量较小，诱导的层流分离受影响较小；当缝隙达到一定宽度后，分离区开始受到显著影响，分离区面积随着缝隙间距呈线性减小的趋势。

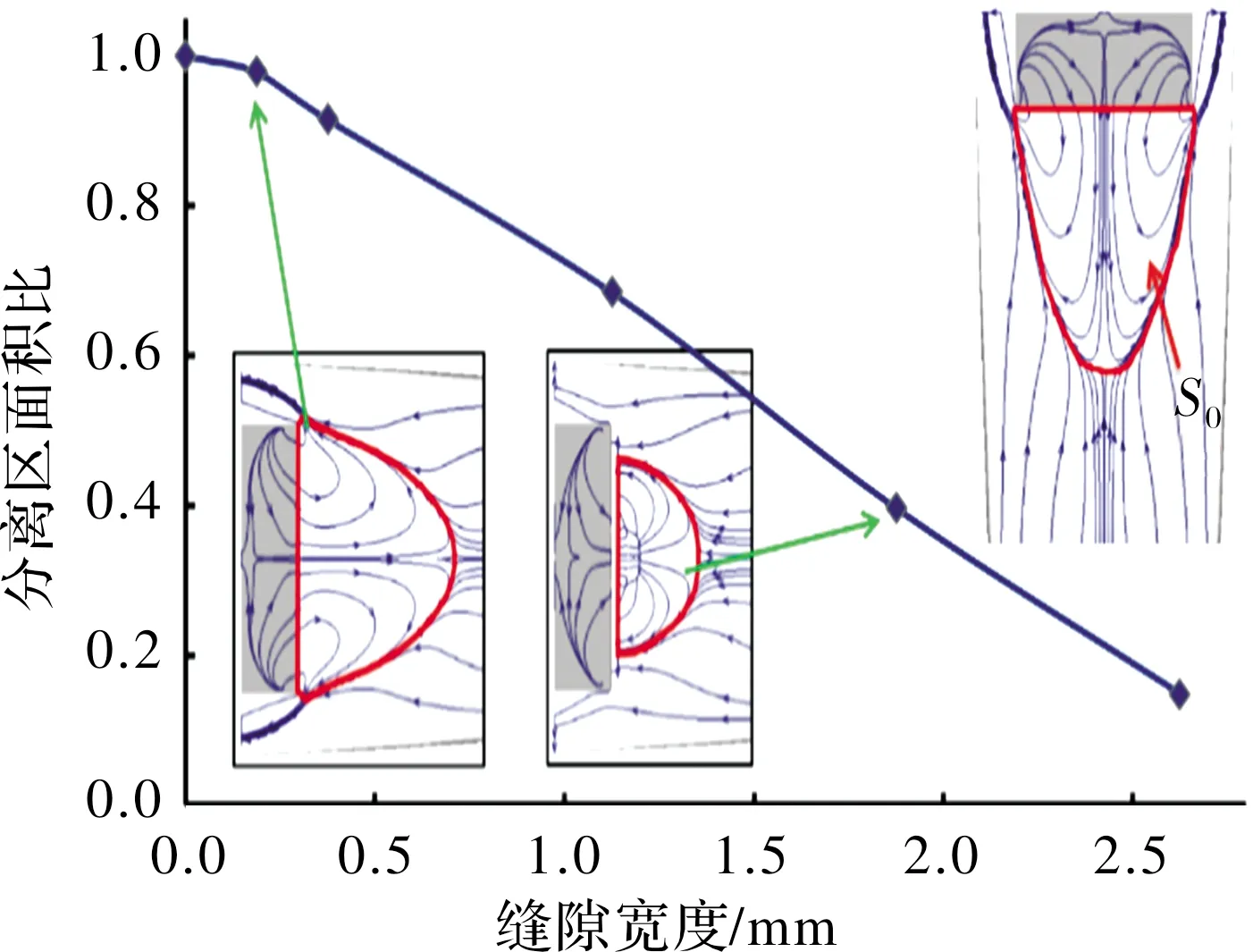
图7 不同缝隙宽度控制翼诱导分离区面积比(S/S0)

图8给出了不同缝隙宽度下飞行器迎风面对称中线的压力分布曲线。由图可以看出，随着缝隙宽度增大，控制翼诱导分离距离缩短，分离区压力平台范围减小且压力上升值下降；而由于分离范围减小，控制翼表面受到高速来流作用增强，表面压力随缝隙增大呈上升趋势。

图8 不同缝隙宽度下迎风面中心对称线压力分布

2.2 舵偏角的影响分析

在控制翼20°舵偏角的基础上，生成15°和25°舵偏角计算模型。给定前缘缝隙宽度=1.875 mm(=6.0)，在原网格结构和分布的基础上，局部调整生成计算网格。来流条件与前文一致。

图9给出了3种舵偏角下控制翼附近极限流线以及压力等值云图，其中上半部分为前缘存在缝隙，下半部分为前缘无缝状态。

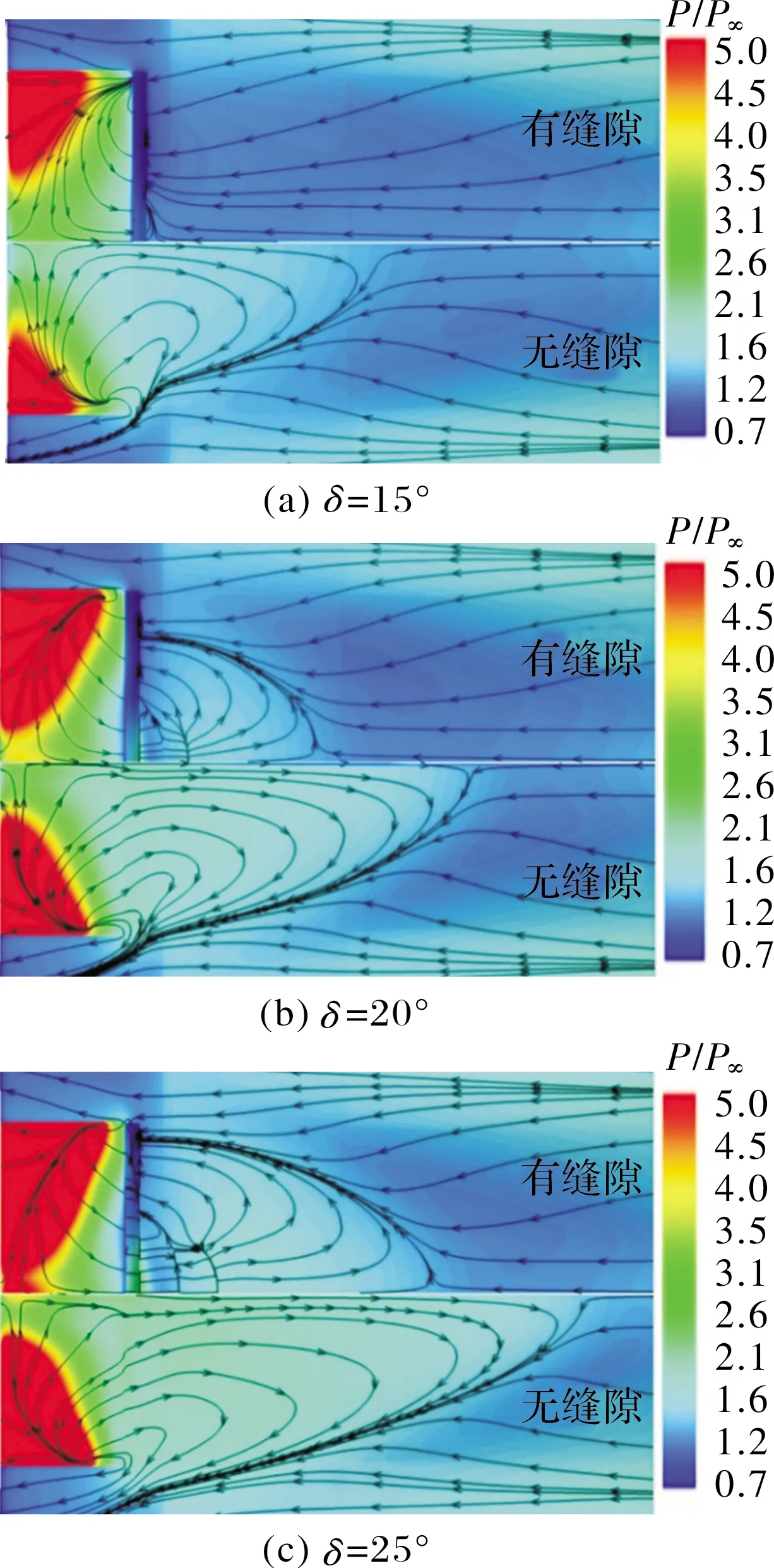
图9 不同舵偏角下控制翼附近流动

由图可见，在给定缝隙=1.875 mm、控制翼舵偏角=15°时，其分离区范围极小，仅存在于前缘中心位置(图9(a))；若控制翼舵偏角进一步减小，控制翼诱导的层流分离将完全消失，给定缝隙下控制翼诱导层流分离，初始舵偏角相对无缝状态增大。此外，相同缝隙下，随着舵偏角从一定值开始减小，分离区相对无缝状态减小幅度越来越大。

2.3 攻角的影响分析

给定控制翼舵偏角=20°，缝隙宽度=1.125 mm(=4.0)和1.875 mm(=6.0)，研究存在前缘缝隙时，控制翼诱导的层流分离流动随攻角的变化规律。来流条件与前文一致。

图10给出了前缘缝隙宽度=1.125 mm时，不同攻角下飞行器表面压力等值云图及迎风面极限流线图谱。考虑到随着攻角变化，波后压力不同，为了更好进行对比分析，选择各攻角下底面对称中线=150 mm处压力值作为参考量进行无量纲处理。

从图10(a)～图10(c)可以看出,当攻角从0°向5°增加，分离区形态相似，分离范围略有增大趋势；继续增大攻角至7.5°，分离范围开始减小，见图10(d)；而当攻角从7.5°变化至10°，分离范围发生骤减，见图10(e)；攻角增大为12°，控制翼诱导分离基本完全消失，见图10(f)。在控制翼面上，随着攻角进一步增大，流线图谱基本类似，而高压区从两角点慢慢向中间延伸，翼面压力上升，由此形成的控制力/力矩增强。

图11给出了=1.875 mm时，不同攻角下飞行器表面压力等值云图及极限流线图谱。通过对比发现，所呈现的变化规律与=1.125 mm基本一致，由于缝隙宽度增大，抽吸增强，在攻角=10°时，控制翼前体分离区基本消失。

可见，在相同缝隙下，随着攻角增大，控制翼诱导分离范围先略有增大而后减小，当攻角增大至一定值，分离范围减小趋势加快，分离范围急剧向前缘中心位置缩进直至完全消失；缝隙宽度越大，控制翼诱导分离流动完全被抑制，初始攻角减小。

图10 不同攻角下压力等值云图及极限流线图谱(Δ=1.125 mm，R2/R1=4.0)

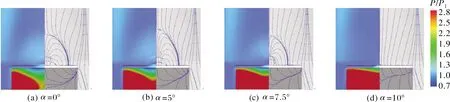
图11 不同攻角下压力等值云图及极限流线图谱(Δ=1.875 mm，R2/R1=6.0)

3 结论

针对控制翼前缘根部缝隙，数值研究了不同前缘缝隙宽度控制翼诱导层流分离流动特性，并给定缝隙宽度分析了不同舵偏角和攻角对控制翼诱导层流分离的影响规律。主要结论如下：

1)前缘缝隙宽度较小，对控制翼诱导分离影响较小，缝隙增至一定宽度，分离区内积聚流体经缝隙抽吸流向后体流量增大，分离区向前缘中心缩进，分离范围呈线性减小趋势，直至消失。

2)一定缝隙宽度，各舵偏角下控制翼诱导分离范围较无缝状态小，其初始分离角较无缝状态增大；相同缝隙下，随着控制翼舵偏角从一定值开始减小，分离区相对无缝状态减小幅度越来越大。

3)相同缝隙宽度，随着攻角增大，分离范围先增后减，当攻角进一步增大，分离范围减小趋势加快，分离区向前缘中心位置缩进直至消失；缝隙宽度越大，分离流动完全被抑制的初始攻角越小。