涉及导函数与分担函数的全纯函数正规定则
许会会,叶亚盛
(上海理工大学理学院,上海 200093)
1 引言与结论
设D为复平面 C上的一个区域,f(z),g(z)为区域D上的两个亚纯函数,若f(z)−a(z)与g(z)−b(z)在D内有相同的零点,则记为f(z)=a(z)⇔g(z)=b(z).文中所采用的Nevanlinna理论和正规族的基本概念与记号等同文献[1-3].
文献[4]证明了一些重要的Picard型定理,并在此基础上提出了相应的正规族猜想[5].自此围绕着这些猜想,正规族的研究取得了很大的发展.
特别地,文献[6]在分担值的条件下,证明了如下定理:
定理 1.1设F为区域D上的亚纯函数族,k∈N+,b∈C,b0,h为有穷正数.如果对于任意f∈F,f的零点重级≥k,且满足:
(2)对任意f的零点,0<|f(k+1)(z)| 那么F在区域D上正规.这里f(a)={z∈D:f(z)=a}. 作者在文献[6]中给出了反例说明当k=2时,定理中的条件(2)是不能省略的.本文在k2条件下,将定理1.1推广为分担亚纯函数的情形,提出一类全纯函数的正规定则,略去了定理1.1中条件(2)的上界条件. 定理1.2设F是区域D内的全纯函数族,k(2)为正整数,a(z)为D内极点均为重级的亚纯函数.若∀f∈F,f的零点重级均≥k,其判别零点个数至多为t,且满足 (1)f(z)=0⇔f(k)(z)=a(z)⇒|f(k+1)(z)−a′(z)|>0; (2)f(z)与a(z)不同时为零, 那么F在区域D上正规. 例1.1设,则 但F在z=0处不正规.例1.1说明了极点重数大于1的条件是必须的. 本文主要参考文献[7-13]的证明方法对定理 1.2进行证明.不失一般性下文中设D=Δ,z0=0. 证明这里只证明F在a(z)的零点处或重数>k的极点处的正规性(重数≤k的极点处的正规性的证明采用了文献[7]的证明方法,过程与引理2.2类似,故这里不再赘述).不妨设z=0为a(z)的零点或重数>k的极点. 情形1:若a(0)=0,不妨设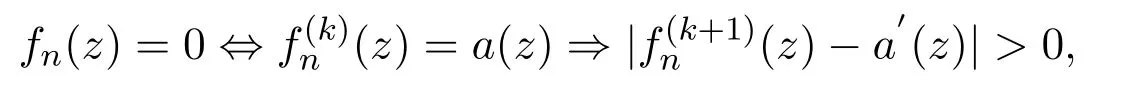
2 几个引理





3 定理证明





