基于强化学习的写字楼动态电力价格策略

樊园杰， 张磊， 吴利刚， 周倩， 张梁

(1. 山西大同大学商学院， 大同 037004； 2. 山西大同大学煤炭工程学院， 大同 037004;3. 山西大同大学机电工程学院， 大同 037004； 4.安徽省智能机器人信息融合与控制工程实验室， 芜湖 241002)

2021年，国家电网发布“碳达峰、碳中和”行动方案。面对新能源快速发展的机遇与挑战，国家电网将以“碳达峰”为基础前提，“碳中和”为最终目标，通过供给侧结构调整和需求侧响应的“双侧”发力，解决“双高”“双峰”问题，推动能源清洁低碳高效利用[1-2]。大力发展可再生能源已成为国家在资源方面的整体战略趋势，尤其是太阳能和风能的利用。然而可再生能源发电的间歇性、波动性和电力消费即时性之间存在的矛盾以及储能的技术经济壁垒，使得可再生能源发电的大规模利用仍然存在障碍。智能电网[3-5]集信息、通信、智能控制技术于一体，融合了分布式发电和负载需求响应，实现了可靠、高效、清洁、自愈、安全等特点的全新电网运行模式。在电力分级市场中，单依靠增加电力系统的传输设备数量来减少电网波动行是行不通的。通过需求侧动态价格响应来灵活的处理不同时间段电力资源供需不匹配问题，从而提高电网的可靠性、安全性并且降低电力资源能耗成本，成为当前研究的热点[6-8]。

基于需求侧动态价格响应是一种及时调整电价的商业策略，目的是通过时变的电价可以改变消费者的用电习惯，从而实现电力的分流、削峰和填谷。文献[9]考虑分时电价的家用电器能耗调度问题，可有效地降低用户成本，提高能源有效利用率。文献[10]研究了大规模使用强制的分时电价对商业和工业领域的影响。而如何制定电价是电价体制改革的关键[11]，为此，朱天博等[12]采用区块链技术保障市场规则的正常运行以及用户的个人利益，进而保障交易的可靠性、安全性。文献[6]则是将能源系统中微电网的动态需求响应策略转化为以零售商利益最大化为目标的混合整数规划问题。为了使得电力零售商利润最大化[13-15]，零售商和用户之间可通过Stackelberg博弈模型进行建模，用户根据公布的价格管理家用电器的能源使用，使其支付最少的费用[16-18]。

现研究分级电力市场中，由物业和写字楼所组成的微电网配电系统。物业作为写字楼消费者与电网公司之间的桥梁，在保证供需平衡的前提下，如何提高电网的可靠性和降低消费者成本成为核心问题, 而如何充分调动需求侧资源，推动电力系统由“源随荷动”向“源荷互动”转变是电力系统安全稳定运行面临的新挑战，受到研究人员的广泛关注。

1 系统模型

如图1所示，将国家电网-物业电力管理部门-写字楼视为一个电力传输的分级电力市场，其中，国家电网是电力供应的起始端，负责电力的产生与传输；物业电力管理部门(property power management, PPM)介于国家电网与写字楼消费者之间，作为保障电力供应与信息传输(电力价格、电力能耗、不舒适度)的枢纽，在电力供需中既要保持供需关系的平衡，维持电力系统稳定；又要实时监测电力需求，根据电力需求通过电力零售价格来约束电力资源的使用。在上述的电力传输与信息交互的过程中，物业的工作状态分为电力高峰期、低谷期和过渡期。

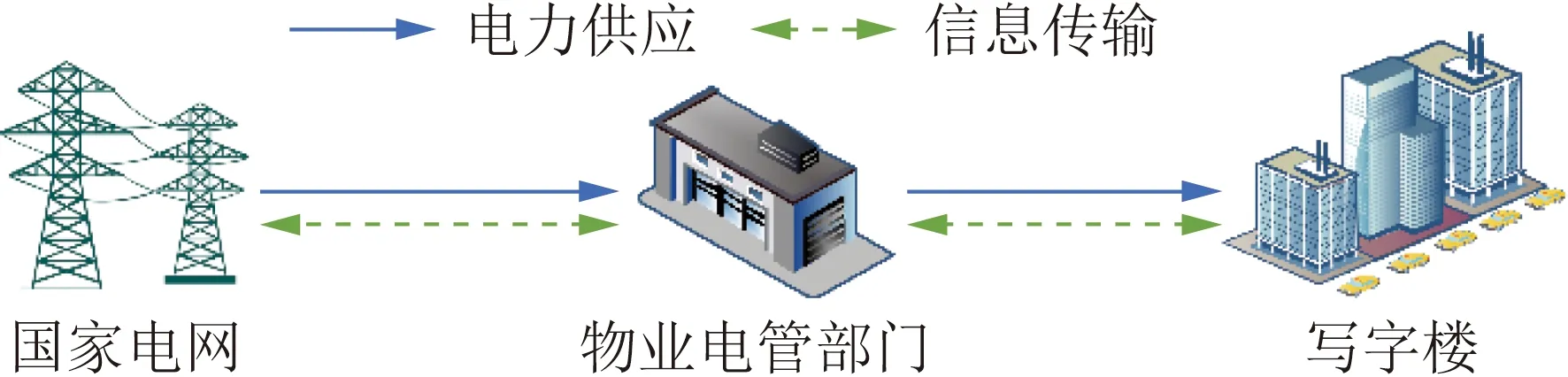
图1 分级电力市场Fig.1 Hierarchical electricity market

物业以电力批发价从国家电网购买电力，同时接收电力供应“紧张度”和写字楼的电力需求信息；物业通过实时计算，根据写字楼的需求信息、电力批发价格以及电力“紧张度”给出实时的电力零售价，完成电力供应的同时将该信息传输给写字楼； 研究重点是物业如何通过所接收到的信息制定合理的动态电价策略，从而改变写字楼消费者的用电习惯，在保障供需平衡的前提下，提高电网的可靠性和降低消费者的购电成本。

1.1 写字楼模型

写字楼内各电气设备在不同的时间段内对电力的需求是不同的，将写字楼中所有的电气设备耗电情况视作一个整体，只考虑写字楼整体的电力能耗情况，暂不考虑各电气设备的具体能耗。

根据用电设备对电量消耗的需求特性，可将写字楼用电设备分为不可调度负载与可调度负载。不可调度负载指的是办公楼部分电气设备由于其工作性质的特殊性，电力供应不可中断也不可缩减的负载，如办公、照明、电梯等；可调度负载指的是可以临时缩减电力能耗的柔性负载，如空调、加湿器、电动汽车集群充电等。因此，不可调度负载模型可表述为

(1)

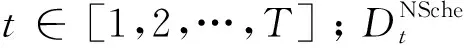
在t时刻，可调度负载的模型可表述为

(2)

(3)

(4)

ζt≤0，ζt∈[0,1]

(5)

(6)

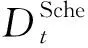
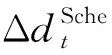
(7)

αt>0；βt>0；αt,βt∈[0,1]

(8)

式中：αt为消费者个人偏好程度参数，αt的值越大，说明写字楼消费者对于电力资源的需求也越大，物业应该尽最大的可能满足消费者的电力需求，反之亦然；βt为预定义的不舒适度参数。

最后，写字楼在t时刻总的能量消耗模型可表述为

(9)

(10)

式中：dt为写字楼用电负载在t时刻总的能耗量；d为在T时间段内写字楼用户负载总的能耗量。

综合考虑电力零售价格、电力实际能耗量、用户不舒适度等诸多因素，定义写字楼用户的目标函数为

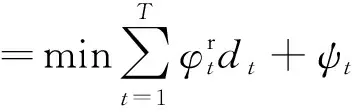
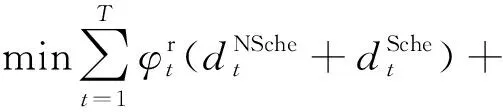
(11)

1.2 物业模型

物业作为写字楼消费者与电网公司之间的桥梁，是一个营利性的中介组织，以最大化自身的收益为最终的目的。定义物业获得利润的目标函数为

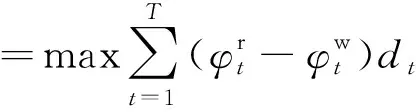
(12)

(13)

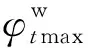
1.3 目标函数

综合考虑物业与写字楼用户端双方利益，定义总目标函数为

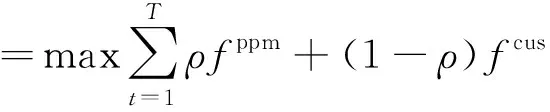
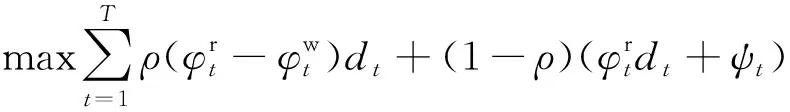
(14)

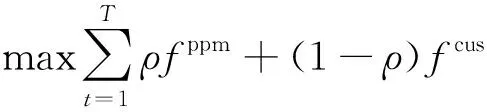
2 基于强化学习的动态价格响应算法

如图2所示，强化学习是智能体在与未知随机环境的信息交互中，通过采取相应的动作以获取最大即时奖励或者累计奖励的过程，适用于求解模型未知的决策问题。

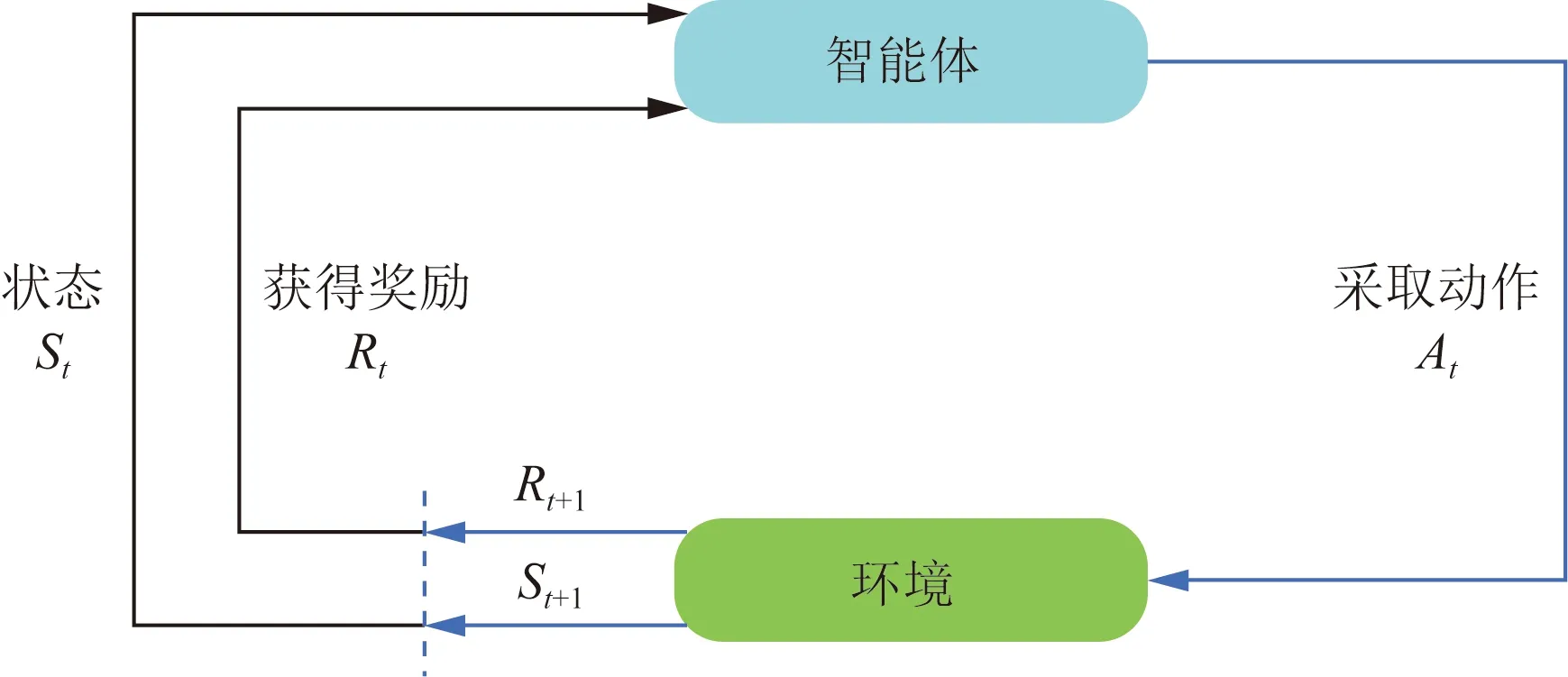
St为智能体在t时刻从环境接收到的实时状态信息；At为当环境处于St状态时智能体采取的动作；Rt为智能体采取At动作时所获得的奖励图2 智能体与环境的交互Fig.2 Interaction between agent and environment

2.1 分级电力市场的MDP模型

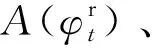
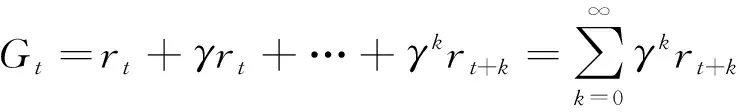
(15)

式(15)中：rt为t时刻所获得的奖励值；γ为未来奖励相对于目前奖励的折扣率；γk∈[0,1]为权衡因子，用于衡量当前奖励与未来奖励的相对重要性。

定义状态-动作价值函数为

Qπ(s,a)=Eπ(Gt|st=s,at=a)

(16)

式(16)中：Qπ(s,a)为在状态s下采取动作a后获得累计回报的期望值；st、at分别为t时刻的状态与该状态下采取的动作；Eπ(·)为在策略π下采取本次动作的期望值；策略π为状态到动作的映射，动作与状态是一一对应的，表征该状态下采取该动作的概率大小。

状态-动作价值函数通过贝尔曼方程(Bellman equation)分解为当前奖励与未来奖励两部分。，即

Qπ(st,at)=Eπ[rt+γQπ(st+1,at+1)|st,at]

(17)

式(17)中：st+1和at+1分别为下一时刻的状态与动作。

式(17)表明当前状态-动作的价值只与当前的奖惩值以及下一步的状态-动作价值有关，而与其他因素无关；因此，通过贝尔曼方程的迭代可求解最佳动作，获得最优策略π*，即

Q*(s,a)=maxQπ(s,a)

(18)

(19)

式中：Q*(s,a)为在状态s下采取动作a所对应Q值的最优解。

2.2 采用Q-Learning求解动态零售电力价格

Q-Learning算法是一种广泛应用的强化学习方法，采用s-a表格的形式记录整个学习过程的Q(s,a)，在整个学习的过程中利用贝尔曼方程迭代更新Q(s,a)值，并通过比较获得最佳的动作a，具体迭代更新可表示为

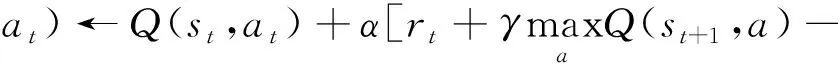
Q(st,at)]

(20)

式(20)中：α为学习率。

表1为Q-Learning算法。为了保证智能体在与新环境的交互中，既能选择最优的行为策略，而且具有对未知环境随机的探索能力，一般选择贪婪策略(ε-greedy)，其中ε∈[0,1]为区间内的常数，当θ<ε时，智能体通过随机选择动作来探索未知环境，其中θ为随机生成的数值；相反，当θ≥ε时，智能体通过利用现有的已知来选取当前状态下具有最大价值的动作[12]，因此智能体的学习满足：

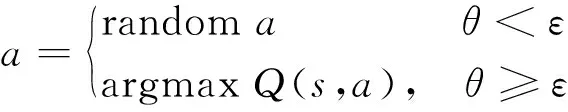
(21)

3 数值模拟

3.1 数值模拟参数与环境设置

数值模拟以一典型的写字楼日常能耗为例，将该写字楼每24 h定为一个时间周期，共计仿真3个时间周期；在每个周期中，每隔1 h进行一次数据结算与信息更新。

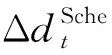
表2 弹性系数参数Table 2 Elastic coefficient parameter

表3 电力价格Table 3 Electricity price

函数中折扣衡量当前奖励与未来奖励的相对重要性权衡因子γ=0.9；贪婪算法中ε=0.5。

数值模拟在Windows10专业版64位以及Core i9-10900k@3.7 GHz，NVidia GeForce RTX 3080硬件下完成，通过Python 3.8.5进行测试。写字楼用户数值模拟以24 h为一个时间周期，在3次数值模拟中算法运行时间分别为：17 619.26、17 721.58、12 575.40 s。

3.2 模型能耗分析

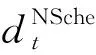
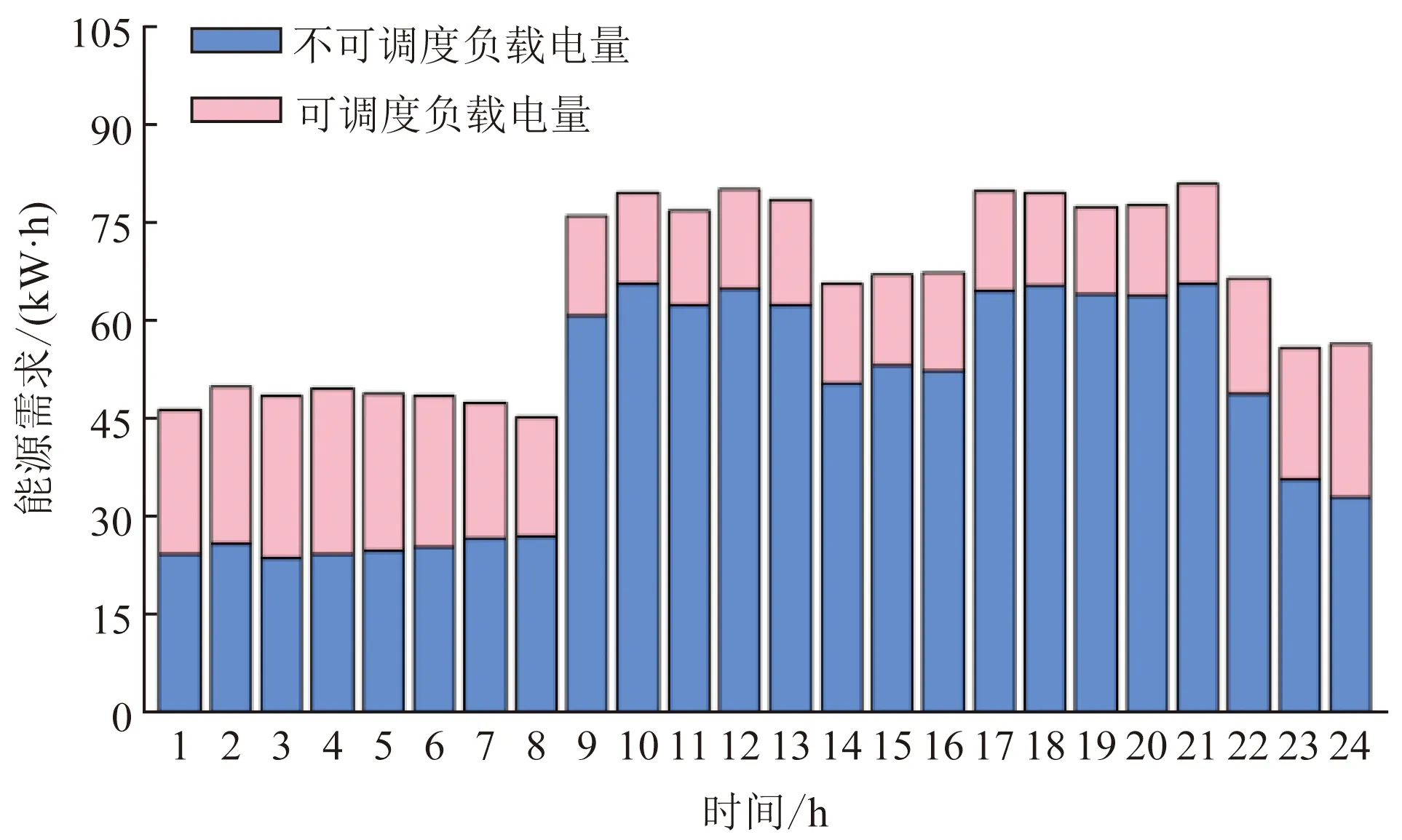
图3 写字楼电力能耗需求Fig.3 Power consumption demand of office buildings

实验中，不可调度电力资源不受电力零售价格的影响，因此在图5中只显示实时电力零售价格信息与可调度电力资源的电力能耗信息；以24 h为一个时间周期，仿真实验中每小时为一个时间节点，共模拟3个周期。可见电力零售价格的波动性整体保持稳定，在电力高峰期与过渡期的电力价格差整体高于电力低谷期，其目的是在电力能耗的高峰期约束写字楼消费者的电力消耗，通过提高价格来缓解电力供应紧张的形势，旨在减小电力“紧张度”。模拟实验表明：电力低谷期(0:00—8:00、22:00—24:00)电力零售价格偏低，可调度电量的使用量普遍偏高，但是综合考虑写字楼的工作时间，得出：可调度电量并不需要被全部供应；相反，在电力高峰期(9:00—13:00、17:00—21:00)写字楼内电气设备高负荷运转，可调度电量有被完全供应的需要，但是受制于电力“紧张度”的原因，在电力高峰期可调度电量不能被完全满足。

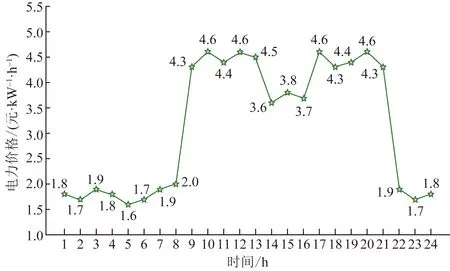
图4 电力价格曲线Fig.4 Electricity price curve

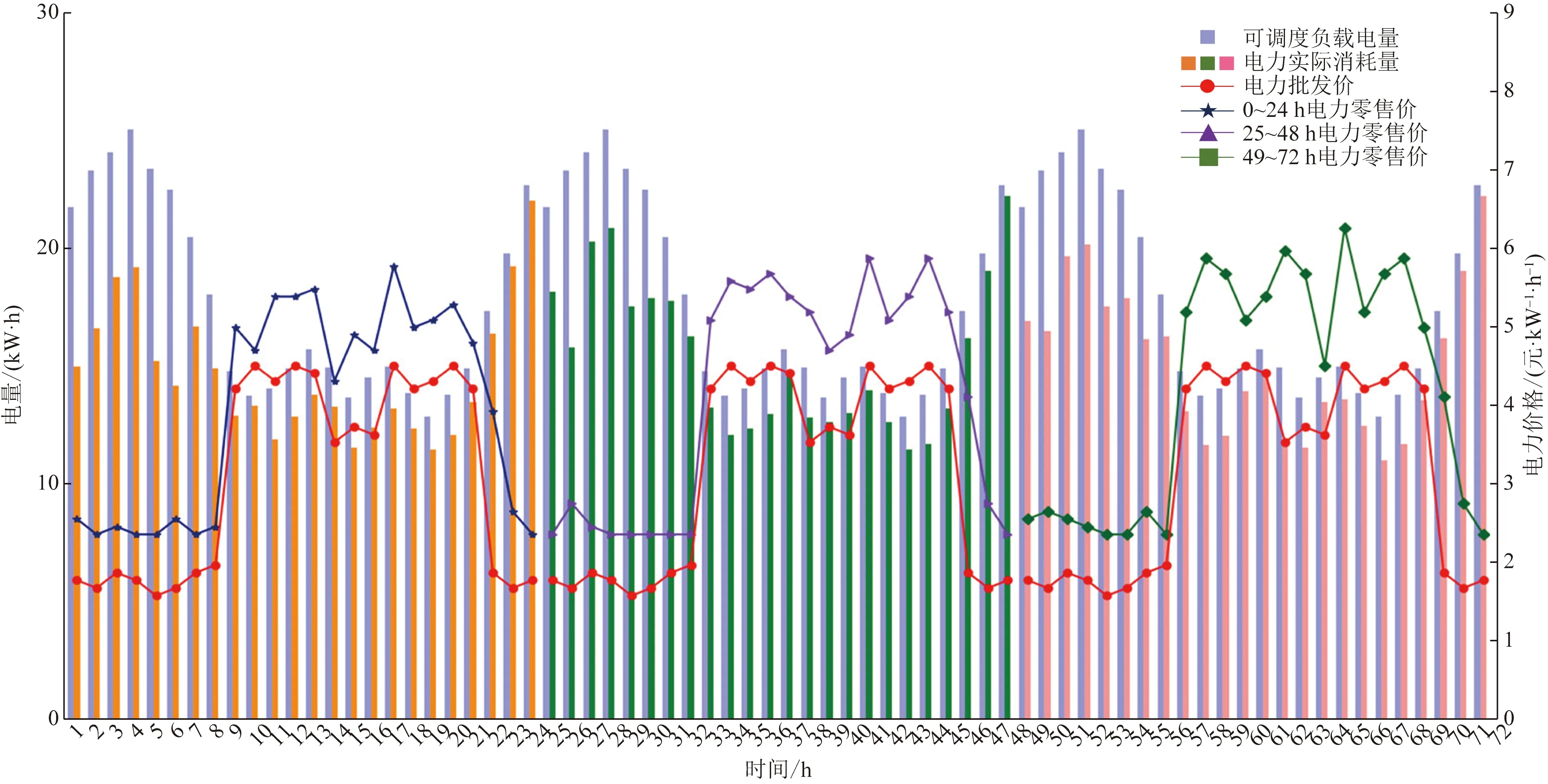
图5 需求侧可调度能源与电力零售价格响应Fig.5 Demand side adjustable energy and retail price response of power

由图5可知，在0～24 h，在电力低谷期6：00的时候节省的电力资源最多，而物业则是在电力高峰期13：00获利最多；在25～48 h时间段内，4：00—8：00的电力零售价格维持恒定均为2.4元/(kW·h)，间接证明该算法在处理电力能耗与电力批发价格之间不失一般性的能够给出相同的电力零售价格；同样地，物业在电力高峰期17：00获利最多；在25～48 h与49～72 h，在电力低谷期2：00的时候，电力资源缩减量最多；每24 h中，电力资源节省量最高时刻分别为6：00、2：00、2：00。分析图6可知：在3个时间周期中，电力资源缩减量分别为74.60、58.32、64.11 kW·h。

通过数值模拟发现，由于写字楼的办公属性，电力资源缩减量在电力低谷期普遍偏高，而物业则是在电力高峰期获取相对较高的收益，说明电力资源缩减量与物业的收益没有特定的线性关系；电力零售价格的波动受到弹性系数ζt与电力资源能耗需求的影响；在弹性系数跳跃性变化时，价格波动明显，电力资源缩减量的变化也更为突出。每24 h电力资源缩减量的能耗对比如图6所示。

图6中，每日可调度电力资源实际能耗保持在约370 kW·h，电力资源缩减量也相对稳定，证明该算法在实际应用中能够有效地处理现实问题，并且在处理相同的问题时，虽然目标函数会秉承消费者成本支出最小和物业利益最大的原则，但是在3个周期内，相同时间点却给出不同的电力零售价格，说明该算法在应对相同问题时，目的虽然相同，但是能够给出不同的解决方案。

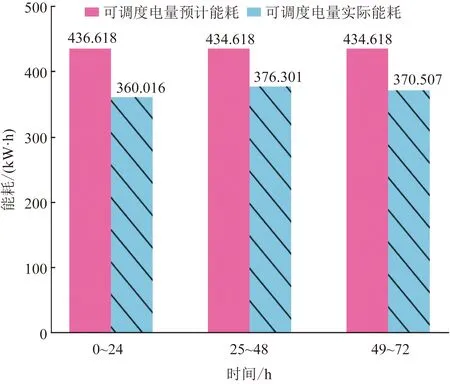
图6 72 h能耗对比Fig.6 Comparison of 72 h energy consumption

3.3 经济效益分析

图7中呈现了写字楼消费者在每24 h中的电力能耗缩减与能耗支出成本的节省。图8中对比了写字楼消费者的成本节省与物业电管部门的盈利收益，通过对比发现，物业盈利与消费者成本节省二者是反比例关系，符合电力市场的现实关系。综合分析可知，在0～24 h，电力节省量最多，但是物业获取的利润却相对最少，仅为242.31元；而在25～48 h与49～72 h中物业获取的利润分别为306.16、334.69元，说明物业获取的利润与电力资源节省量并非线性关系，间接说明该算法并不是简单地将电力资源缩减量与物业获取利润耦合关联。

结合3.2节模型能耗分析可以得出，基于强化学习的需求侧电力价格响应在3个能耗需求相同，电力批发价格相同的周期中，最终在相同时刻给出了不同的电力零售价格，但是却始终保持了可调度电力资源实际能耗与物业获取利益的相对稳定，说明该算法具有良好的自适应能力与合理解决问题的能力。

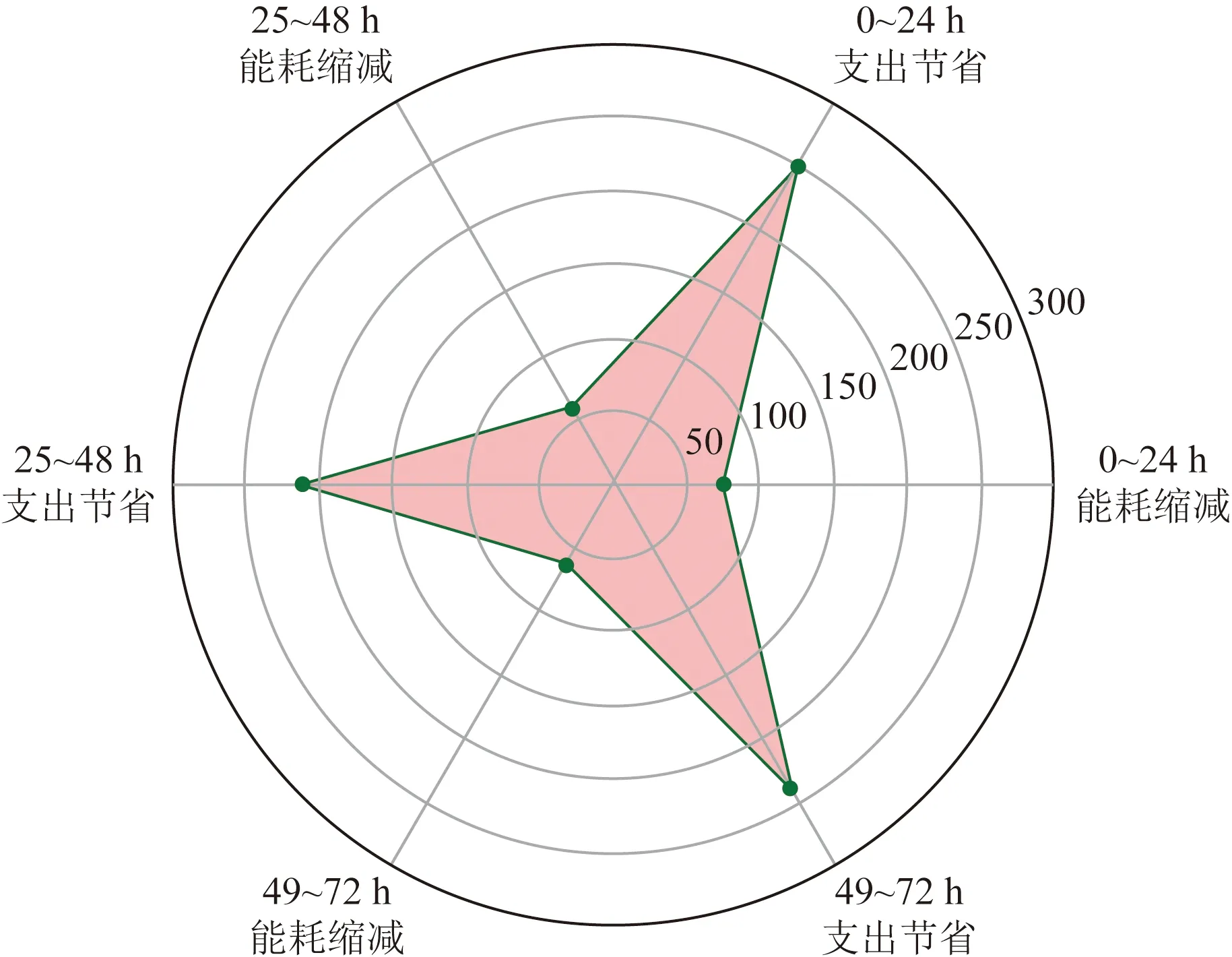
图7 CUS能耗缩减-成本节省Fig.7 CUS energy reduction-cost savings

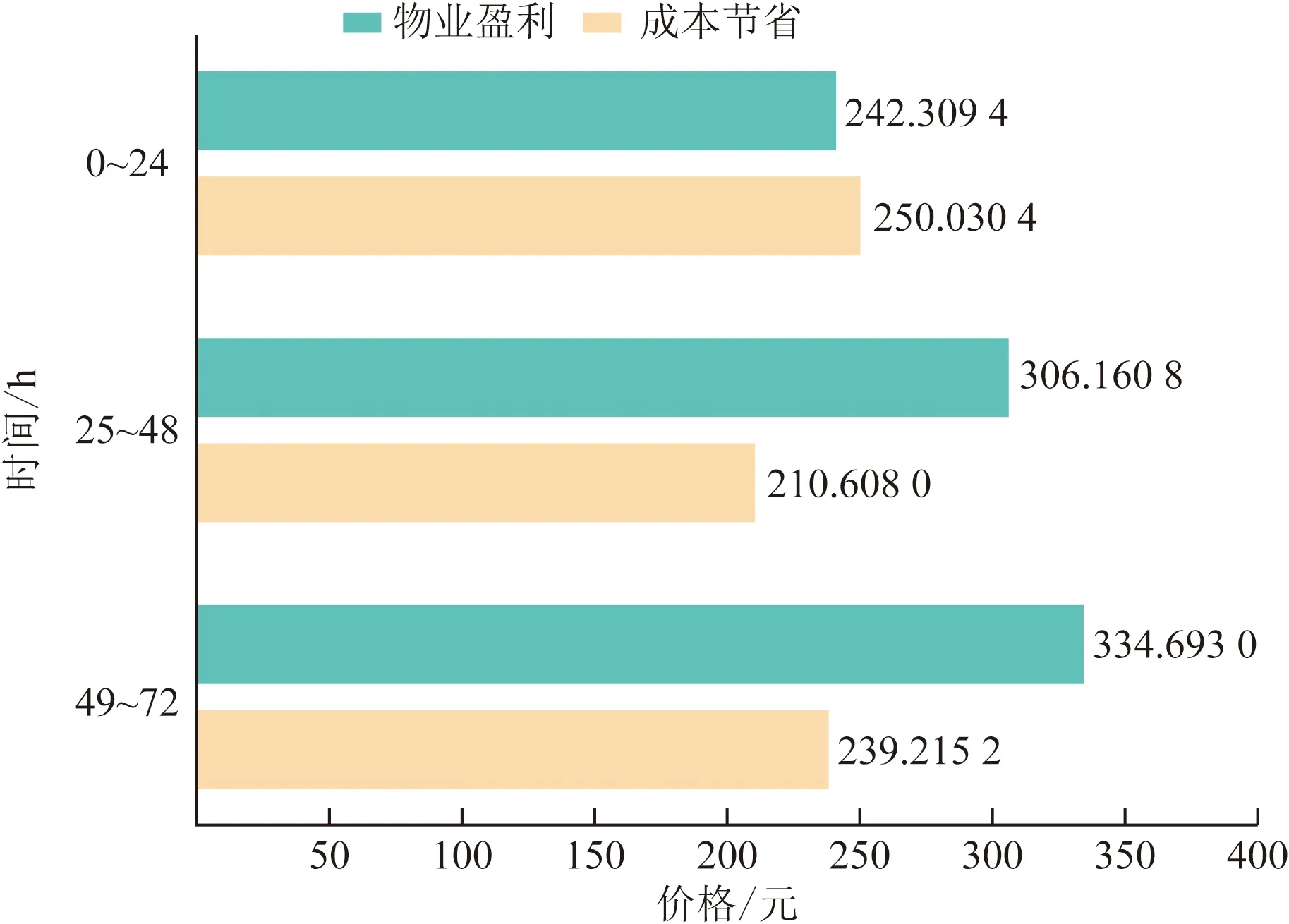
图8 双方利益分析Fig.8 Interests of both parties analysis

4 结论

在微电网能源管理系统中，首先建立以国家电网公司-物业管理部门-写字楼消费者为整体的分级电力市场模型,并将分级电力市场建模为MDP模型，然后通过基于强化学习的需求侧动态价格响应算法获得物业最优的能源调度策略，通过Q-Learning求解最优的动态零售价格序列，在保障写字楼用户正常办公的前提下，不仅节省电力成本，而且最大程度地提高物业的盈利，有效减少电力波动，提高电网的可靠性。以写字楼用户72 h能耗需求与实际能耗为例，通过数值模拟验证，分析电力资源节省量与消费者态度之间的非线性关系，验证了所提算法的有效性和实用性。

仅在以写字楼为例建立离散-有限的MDP 模型中证明了该算法的实用性，后期将继续增加其他电力能耗类型在电力资源调度与能源管理中做整体性分析或局域性调度；特别是在智能电网电力传输与分配方面做深入研究。