采用下垂控制的多端柔性直流输电系统功率可调节范围量化分析

申锦鹏, 李勇汇*, 张玉琼, 赵强, 段勉, 刘佩娴, 杨军

(1.武汉大学电气与自动化学院, 武汉 430072; 2.中国电力科学研究院有限公司, 北京 100192)

中国一次能源与负荷呈逆向分布特征，为满足清洁能源送出、负荷中心电力供应、节能减排等方面的迫切需求，远距离、大容量的特高压直流输电技术得到广泛应用[1-4]。基于模块化多电平换流器的多端柔性直流输电相较于常规直流输电方式，具有功率灵活可控、无换相失败问题、无需功率补偿、谐波含量低、占地面积小等诸多优势，具有广阔的应用前景[5-6]。如同频率稳定对于交流系统的重要性，有效的直流电压控制是保证直流电网稳定运行的重要前提。随着柔性直流输电工程的大量投入，得到了广泛的关注与研究[7]。

针对直流电压控制，目前多端柔性直流输电(multi-terminal direct current transmission，MTDC)采用的系统级控制策略大致分为[8]：主从控制策略、电压裕度控制策略、直流电压下垂控制策略。主从控制具有概念清晰、结构简单、电压质量高等优点，但依赖于控制器间的高速通信，不利于系统可靠性的提高。电压裕度控制可在系统发生大扰动时转换主控站，相较于主从控制可靠性更强，但其控制器设计复杂，同时对电压控制站的容量要求较高。以上两种控制方式通常用于端数较少且换流站容量差别悬殊的小型直流系统中。直流电压下垂控制策略为多点控制，通过测量母线电压依靠本地换流站控制器实现功率的协调分配,不依赖于换流站间的高速通信[9]，提高了系统的可拓展性和可靠性，更适用于换流站数目较多且功率频繁波动的多端柔性直流输电，目前已在实际工程的控制系统中应用[7]。

然而，下垂控制策略功率调节能力有限，直流电压对传输功率的变化较敏感，当出现较大不平衡功率超出其可调节范围时，会导致直流电压越限：其值过高会对电力电子器件、电容器等造成不可逆的损坏，影响系统安全稳定运行；过低会导致直流电流增大，系统损耗增加[10]。针对这一关键问题，诸多研究给出了两类解决方案：控制器下垂系数选择[11-13]和改进下垂控制策略[10,14]。文献[11]通过频域分析确定了MTDC系统下垂系数的选取范围，但换流站节点被建模为简单的电流注入端点，模型精细度较差；文献[12]建立直流电压控制模型，采用劳斯判据确定下垂系数选取范围，分别在时域和频域中分析了控制特性及稳定性；文献[13]以下垂控制参数为决策变量，与调度系统相结合，建立了以系统电压偏差和损耗最小为目标的优化模型；文献[10]通过测量本地电气量引入功率影响因子，使直流电压偏差与直流电流的二次方成正比，在不同运行工况下对下垂系数自适应修正，优化了系统的运行特性；文献[14]提出了一种分层调压策略，下垂控制作为一次调压在扰动结束后0.5 s内起作用，二次调压随即刷新功率指令，维持直流电压基准值。上述研究表明，通过选取恰当的下垂系数或改进下垂控制策略可以显著地减少功率频繁波动造成的直流电压偏差。但一方面，功率传输过程中输电线路上电压降落导致的各换流站间的电压差会影响不平衡功率的调节能力[15]，上述控制器设计方法仅关注于可调功率节点而忽略了其他端口的电压质量；另一方面，MTDC系统具有多输入多输出(multiple input multiple output, MIMO)特性，简单的控制器设计无法处理多变量间的耦合效应，且忽略了系统动态特性带来的影响。总的来说，如何综合考虑多端系统换流站间的电压偏差、多变量间的关系以及动态特性，分析直流电压质量和不平衡功率间的制约关系，量化功率调节范围以保障系统安全稳定运行还处于空白阶段。

针对上述问题，提出了一种下垂控制功率可调节范围的量化分析方法。首先，建立多端柔直系统小信号模型并推导不平衡功率对直流电压影响的传递函数表达式。随后，针对这一多输入多输出系统，基于奇异值分解和频域分析确定功率调节能力极限，保证任意换流站的功率波动均不会使各端点直流电压超过安全运行限制。最后，基于Simulink对所提方法进行了算例分析和仿真验证。

1 直流电压下垂控制MTDC系统小信号建模

1.1 MMC-MTDC系统与下垂控制策略

MTDC系统采用常规环形拓扑(general ring topology， GRT)结构，以风电场接入为例，该系统由风电场侧换流站(wind farm converters, WFCs) 1和2、网侧换流站(grid side converters，GSCs) 3和4以及直流网络组成，如图1所示。该结构能够在故障发生时快速切除相应线路且不损失系统输送功率，继续保持系统稳定运行，控制灵活性较高。

模块化多电平换流器采用子模块级联的方式，具有可拓展性强、输出波形良好、冗余容错控制能力强和效率高等特点，广泛应用于柔性直流输电领域。三相模块化多电平换流器拓扑结构如图2所示。

同相的上下桥臂构成一个相单元Leg，换流器的各桥臂由半桥子模块(submodule, SM)、桥臂电抗器Larm和等效损耗电阻Rarm串联构成。

文献[16]针对模块化多电平换流器(modular multilevel converter，MMC)提出5种简化模型，其中平均值模型(average-value model, AVM)将MMC交流侧用受控电压源等效，直流侧用受控电流源等效，如图3所示，其计算精度及计算性能均能满足暂态仿真要求。注重于对MMC外特性的研究，因而采用AVM简化模型分析。

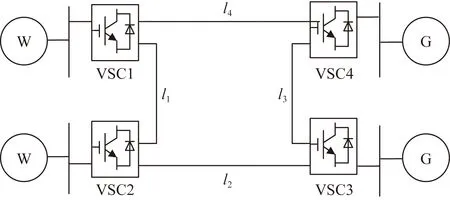
W、G分别为风电场和交流同步电网；VSC1、VSC2、VSC3、VSC4分别为风电场侧和网侧电压源换流站；l1、l2、l3、l4为换流站间直流传输距离图1 MTDC系统常规环形拓扑结构Fig.1 General ring topology of MTDC System

采用下垂控制策略的MTDC系统将直接连接风力发电或光伏发电的不可调功率节点设置为有功功率控制，运行于联网或孤岛模式；将接入大电网的可调功率节点设置为电压下垂控制方式，换流器根据直流电压水平，参照下垂特性曲线移动工作点调整功率参考值，保证直流电压稳定与有功功率合理分配，如图4所示。

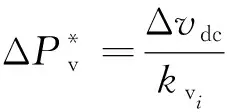
(1)

由式(1)可以看出，直流电压质量与不平衡功率密切相关，为将直流电压控制在允许的运行区间，需要分析功率可调范围对出力波动做出限制。

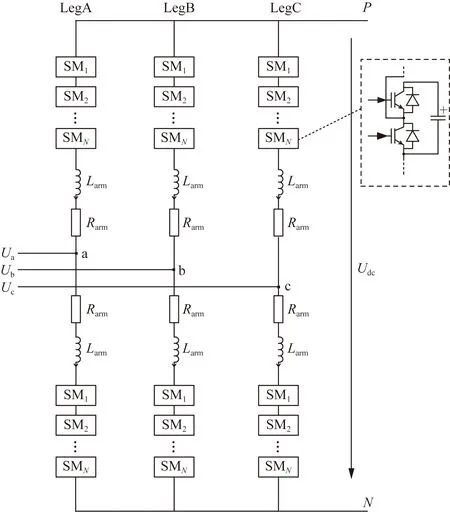
Uk为交流输出电压(k=a,b,c)；Udc为直流电压；P、N为直流母线连接点图2 三相MMC直流输电拓扑结构Fig.2 The circuit topology of three-phase MMC-MTDC

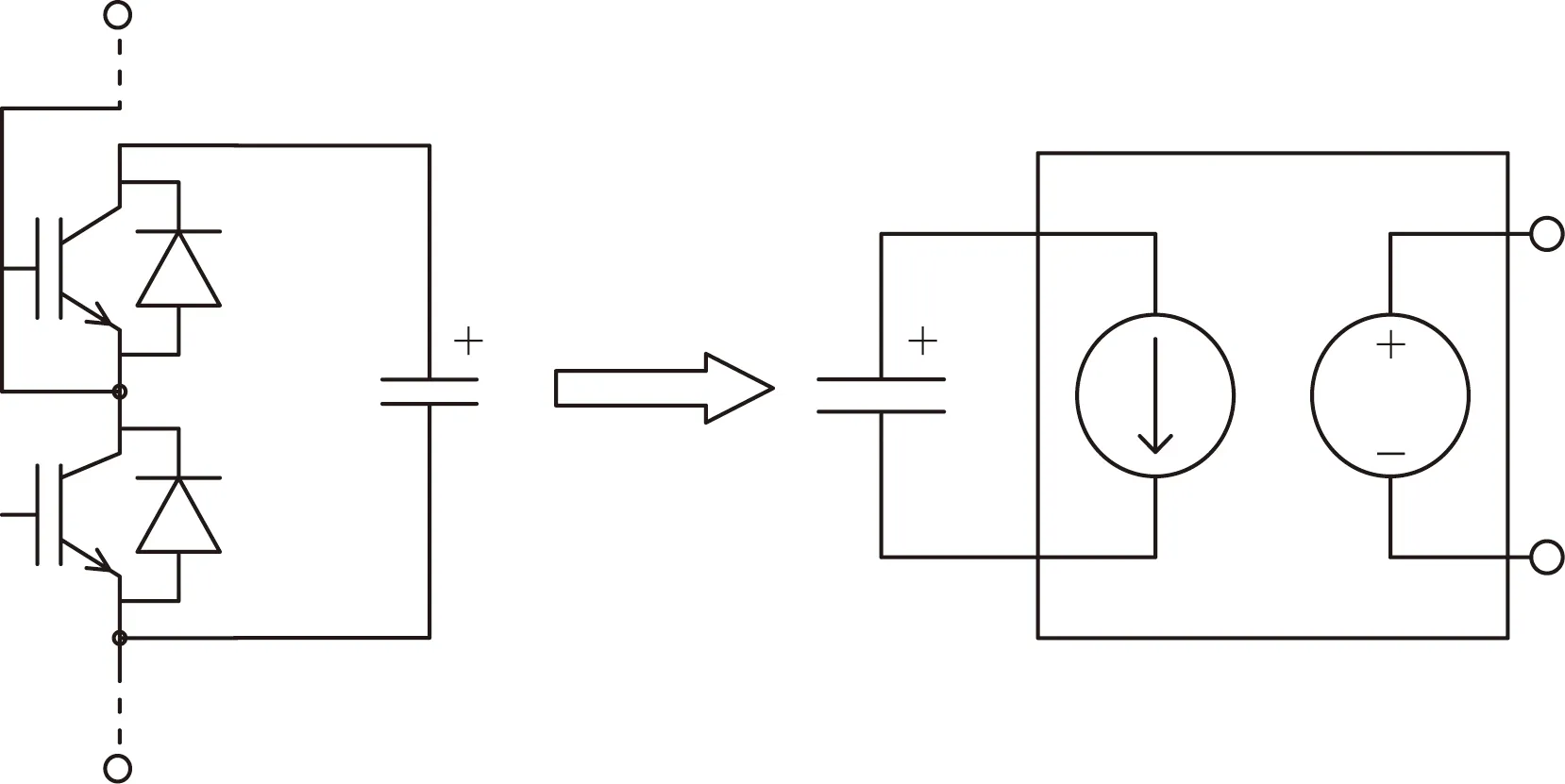
图3 AVM简化模型结构Fig.3 Simplified model structure of AVM

1.2 MTDC系统小信号建模

小信号频域分析法基于传递函数，研究系统在一定输入激励下的输出情况，无需考虑内部复杂结构，同时可以分别从静态和动态角度分析，适用于高维非线性的MTDC系统。对采取下垂控制策略的MTDC系统进行频域分析，首先要构建完整系统的小信号模型，基本步骤如图5所示。

相较于双端系统，多端柔性直流输电系统的模型复杂度更高、建模难度更大，近年来关于柔性直流电网小信号建模的研究已较深入[17-19]。为简化建模步骤、提高在不同结构MTDC系统中建模的普适性，采用将完整系统分解为子系统分别线性化建模，利用互联约束联立方程的方法完成建模过程。该方法在文献[19]中进行了详细分析，以MMC换流站的交流物理子系统为例简述其基本原理。该子系统d-q坐标系下的模型可描述为[20]

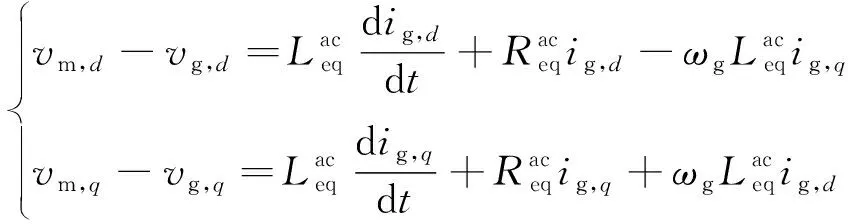
(2)

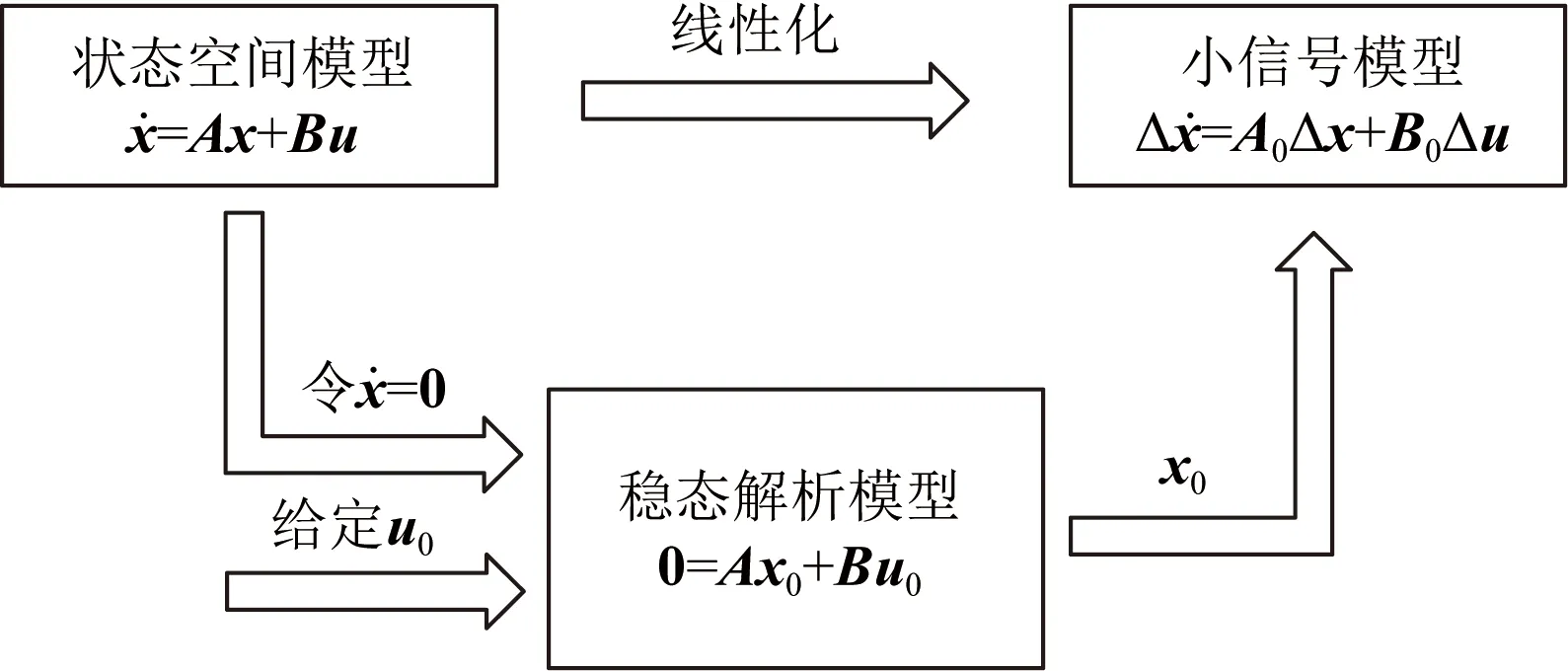
A、B、A0、B0分别为状态空间模型和小信号模型的状态矩阵和输入矩阵；x、u、x0、u0、Δx、Δu分别为状态空间模型、稳态解析模型和小信号模型的输入向量和状态向量；分别为状态空间模型和小信号模型状态向量的导数图5 小信号建模原理图Fig.5 Schematic diagram of small signal modeling

首先根据控制策略和拓扑结构，生成换流器的稳定运行工作点。其次，将该系统在工作点附近小信号近似线性化：x=x0+Δx。在小信号假设下：ig,d=Ig,d0+Δig,d、ig,q=Ig,q0+Δig,q、vm,d=Vm,d0+Δvm,d、vm,q=Vm,q0+Δvm,q及ωg=ωg0+Δωg。其中，Ig,d0、Ig,q0、Vm,d0、Vm,q0分别为d轴和q轴稳定运行点的交流电流和差模电压，Δig,d、Δig,q、Δvm,d、Δvm,q分别为d轴和q轴稳定运行点周围的交流电流和差模电压偏差；忽略二次项，式(2)可表示为

(3)

令输入变量为Δvm、Δvg、Δωg，输出变量和状态变量为Δig，即可得到该子系统的小信号模型。将各换流站的交直流物理系统、内外环控制器、锁相环以及直流线路等n个子系统均按上述原理在稳定运行点附近近似线性化并用式(4)所示的小信号状态空间方程形式可表示为

(4)

式(4)中：An、Bn、Cn、Dn分别为小信号模型的状态矩阵、输入矩阵、输出矩阵、前馈矩阵；Δxn、Δun、Δyn分别为小信号模型输入向量、状态向量和输出向量。

换流站的交直流物理系统与控制系统、变量计算、锁相环等子系统通过输入输出变量相互连接，如图6所示。根据各模块间输入输出关系构成的互联约束，联立n组小信号状态空间方程，删除内部中间变量简化模型，即可得到全局状态空间方程，由此完成MTDC系统的小信号建模。在完整模型中指定研究对象的输入输出变量，接下来就可以对相应传递函数的激励响应展开分析。

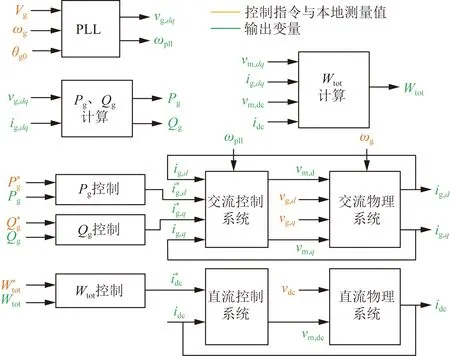
θg0为交流侧电压相位；ωpll为锁相环测得的角频率；分别为交流侧有功和无功功率的测量值和参考值；vm,dc为等效电容电压；Wtot、W*tot分别为电容储能的测量值和参考值；i*g,d、i*g,q分别为d轴、q轴的交流侧电流参考值；idc、i*dc分别为直流电流的测量值和参考值图6 子系统互联约束Fig.6 Interconnection constraints of the subsystems

2 MTDC系统功率可调节范围量化分析方法

2.1 基于奇异值分解的P-V特性分析

奇异值分解方法是多变量系统波特图频域分析的拓展，广泛应用于多输入-多输出系统的分析与设计中，以量化其系统增益[22]，可用于分析有功功率-直流电压之间的关系，该方法原理如下。

对于某固定频率ω，MIMO系统传递函数G(jω)为m×n维矩阵，将其简写为G，进行奇异值分解，可表示为

G=UΣVT

(5)

式(5)中：U和VT分别为m阶和n阶酉矩阵，对应的列向量Ui和Vi称为左奇异向量和右奇异向量；Σ为m×n维矩阵，通过式(6)计算得到的非负奇异值σi[G(jω)]沿主对角线降序排列，其他项均为零。

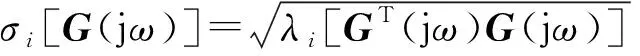
(6)

式(6)中：λi为矩阵GTG的第i个特征值。

奇异向量第一列U1和V1分别为使系统增益最大的输出和输入方向。作为频域分析在MIMO系统的推广，该方法通过计算不同频率ω处的奇异值和矩阵的左、右奇异向量，找到使系统增益最大的输入-输出信号，进而定量地分析多输-多输出系统。

对于采取下垂控制策略的MTDC系统，任一送端换流站产生的有功功率波动均会对各换流站节点的直流电压产生影响，对于图1所示的研究对象，其传递函数模型如图7所示。

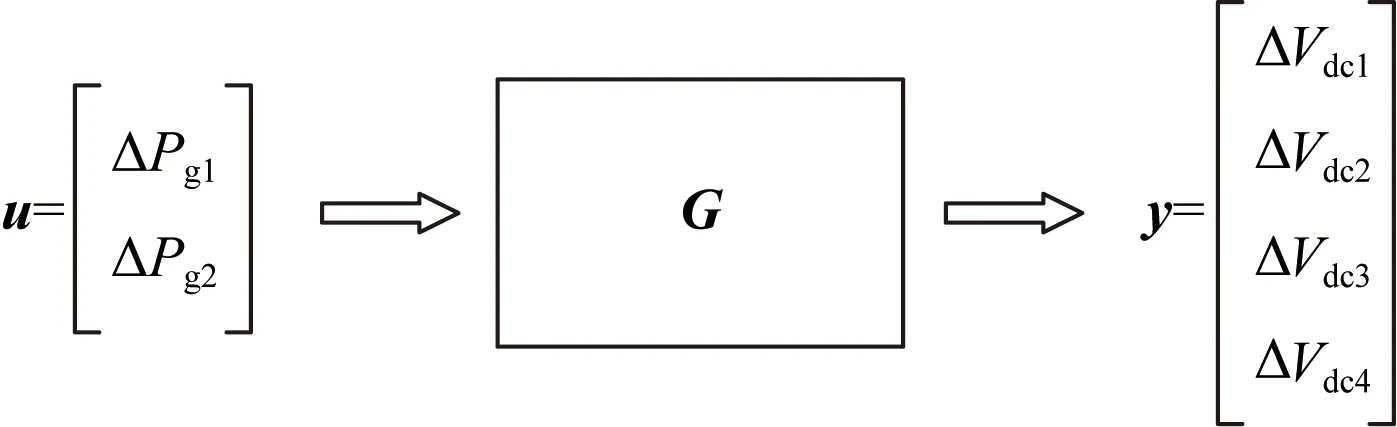
图7 MTDC系统传递函数模型Fig.7 Transfer function model of MTDC system

该模型研究受到送端换流站输出功率波动激励时，4个换流站节点产生的直流电压偏差。因此，传递函数为y(s)=G(s)u(s)，其中y(s)为4×1维输出向量[ΔVdc1ΔVdc2ΔVdc3ΔVdc4]T，u(s)为2×1维输入向量[ΔPg1ΔPg2]T，G(s)为4×2维传递函数矩阵，MIMO系统的增益以范数形式表示为[23]

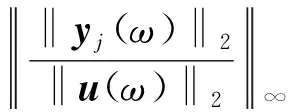
(7)

式(7)中：yj(ω)为传递函数的第j个输出；Δvdcj为第j个换流站的直流电压偏差；gjk为系统从输入k(k=1,2)到输出j方向上的增益。

传递函数矩阵的奇异值σi[G(jω)]表征了系统对输入向量的改变，而输入向量经历的最大增益由最大奇异值σ1i[G(jω)]给出，可表示为

(8)

对于MTDC系统，为保证任何增益方向上的直流电压偏差严格不越限，应对其中的最大增益即最大奇异值进行频域分析。用σ1i[G(jω)]表示不平衡功率-直流电压偏差间的特性关系，继而进行功率调节范围的量化分析。

2.2 功率可调节范围量化分析方法

从静态角度，送端有功控制换流站的出力波动会使受端下垂控制换流站产生可量化的直流电压偏差，通过式(1)就能算得理论上系统可调节的最大不平衡功率。但输电线路上的电压降落会导致各换流站间的电压偏差，因此需要基于奇异值分解，考虑多输入变量的不同组合与多输出变量间的关系，保证所有换流站端口的电压质量。从动态角度，输电线路被建模为π型双回分段传输线，直流电网与换流站间的相互作用可能激发动态行为影响暂态直流电压[24-25]，当功率突变或频繁波动时产生的激励可能与系统固有频率重合发生谐振从而对直流电压造成较大冲击，因此也需要考虑系统的暂态电压。

由2.1节的分析可知，MTDC系统最大直流电压偏差和有功功率波动量之间的关系可以表示为一个增益边界L。式(7)中，换流站允许的最大直流电压偏差已由运行要求确定，那么通过分析最大奇异值σ1i[G(jω)]的幅频特性曲线就可以确定稳态和动态下的增益边界，继而由式(9)计算出满足电压质量要求的功率可调节范围。

(9)

式(9)中：Δvdcmax为最大直流电压偏差；L为增益边界。

基于奇异值分解的功率调节范围量化分析方法原理框图如图8所示。

首先，根据第1节所述步骤线性化子系统、确定输入输出信号并联立方程、构建MTDC系统小信号模型。之后，利用最大奇异值描述P-V特性，通过频域分析研究系统的稳态特性和动态特性，根据直流侧电压约束条件确定系统可调节的最大不平衡功率。最后可以通过暂态仿真验证稳态与动态特性下的量化分析结果。

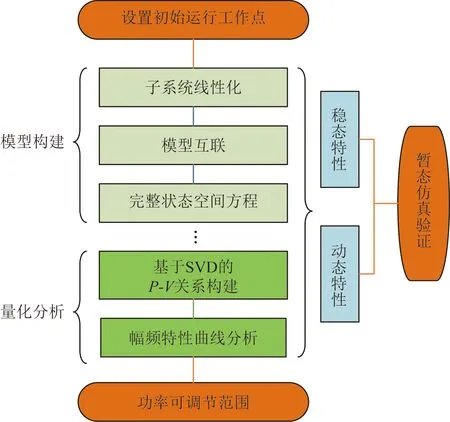
图8 功率可调节范围量化分析框图Fig.8 Block diagram of quantitative analysis of power regulating range

3 算例与仿真分析

3.1 MTDC系统及小信号建模

本算例构建了图1所示的四端MMC-MTDC系统，其中VSC1和VSC2换流站接入风电场，采用有功功率控制方式；VSC3和VSC4换流站与交流同步电网连接，采用直流电压下垂控制方式；各换流站内环控制参数相同，换流器采用图3所示的AVM简化模型。直流线路采用π型双回分段传输线，传输距离为l1=450 km、l2=300 km、l3=600 km、l4=300 km，每150 km分为一段，线路参数如表1所示。

表1 传输线参数Table 1 Parameters of lines

一般工程中的下垂曲线斜率取4%～5%[24]，为简化分析，本算例中VSC3和VSC4换流站的下垂系数设置为相同大小kv3=kv4=-5%。额定直流电压为±500 kV，直流电压应在经济限制±10%[26]或更严格的限制±5%[27-28]的范围内适当调节，本算例选为±5%(950～1 050 kV)。

按照1.2节所述方法对本算例MTDC系统建模，选定图7所示的输入输出变量，最终得到144×144维的状态矩阵A、144×2维的输入矩阵B、4×144维的输出矩阵C、4×2维的前馈矩阵D。与整个系统的小信号建模相比，文献[19]所提方法仅需指定系统模型和运行工作点，建模步骤大大简化，适用于不同控制方式和拓扑结构下的MTDC系统。

3.2 功率可调节范围量化分析

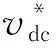
对于容许的最大直流电压偏差Δvdcmax=±5%，其增益边界可表示为

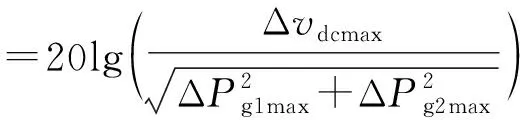
(10)

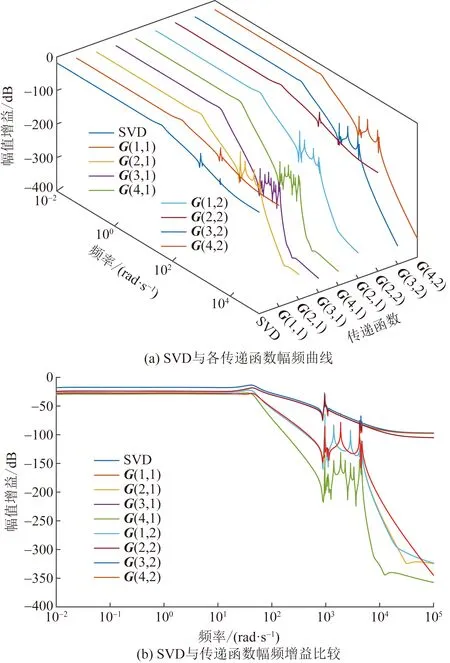
图9 SVD与传递函数幅频特性Fig.9 Frequency characteristic of SVD and transfer function

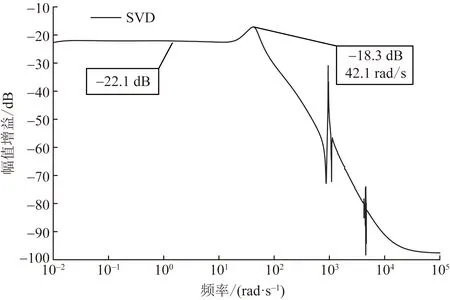
图10 SVD频率响应曲线Fig.10 Frequency domain response curve of SVD

(11)

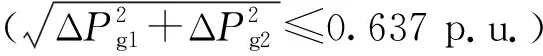
图10中，在较低频率下可以观察到增益峰值的出现，与该频率相对应的特征值表明此峰值由送端换流站d轴控制电流与直流电网间的相互作用产生[24]。当送端换流站以此频率发生功率波动激励系统时，将产生更高的电压增益导致动态直流电压越限，该情况多出现于风电场经柔直并网发生次同步振荡时[29-30]，近年来引起广泛关注。因此从动态角度出发，式(11)并未确定功率可调节范围的唯一条件。42.1 rad/s频段出现了第一共振峰值L=-18.3 dB，此时最大增益方向为ΔPg1∶ΔPg2= 0.865∶0.503，该峰值对应的功率可调节范围为

(12)

3.3 仿真验证

利用MATLAB/Simulink仿真软件搭建图1所示的四端MMC-MTDC系统仿真模型，对所提的分析方法和3.2节的算例分析结果验证。

初始时刻，VSC1和VSC2换流站向MTDC系统传输2 000 MW和1 000 MW的有功功率；在0.3 s时刻，VSC1输出功率增加0.637 p.u.，VSC2输出功率保持不变，持续0.7 s；在1.8 s时刻，VSC1输出功率增加0.519 p.u.，VSC2输出功率增加0.368 p.u.。观察有功功率波动对直流母线电压的影响，各换流站有功功率和直流电压仿真结果如图11所示。

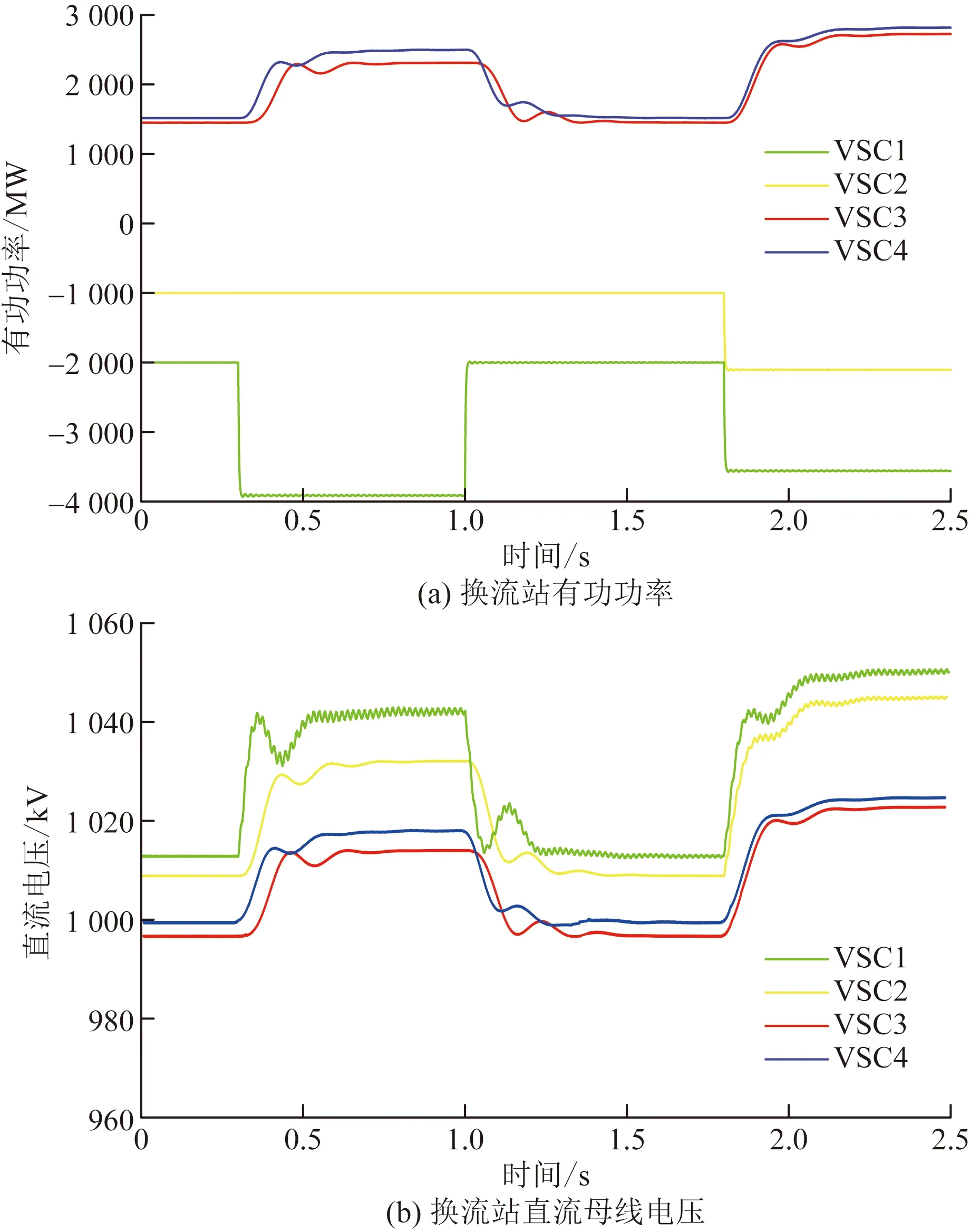
图11 稳态分析结果仿真图Fig.11 Simulation diagram of steady-state analysis results

可以看出，由于传输线上的电压降落，当前稳定运行点下的VSC1及VSC2换流站直流电压分别为1.013 p.u.和1.009 p.u.，与受端换流站相比存在电压偏差。0.3 s时刻系统不平衡功率产生后，下垂控制换流站根据下垂曲线分配有功功率，其电压差和不平衡功率基本满足式(1)所述关系。最大直流电压偏差出现在VSC1换流站，约为4.1%；1.8 s时刻，按照右奇异向量V1产生功率波动，换流站VSC3和VSC4直流电压仍在安全运行范围内，但VSC1换流站已到达5%的偏差边界。统计边界条件下不同输入功率波动比ΔPg2∶ΔPg1对应的最大直流电压偏差如图12所示。

仿真结果说明：换流站间的电压差降低了不平衡功率的调节能力，在下垂控制器未到达其理论调节极限时送端换流站直流电压已经越限；在不同传输方向上不平衡功率造成的系统增益并不相同。因此为保证直流电压始终不越限，应该按照式(11)的计算结果严格确定系统的功率可调节范围。

对动态分析结果进行验证。初始时刻，VSC1和VSC2换流站向MTDC系统传输2 000 MW和1 000 MW的有功功率；0.1 s时，VSC1换流站模拟次同步振荡，产生频率为42.1 rad/s、幅值为0.411 p.u.的正弦波动，VSC2输出功率保持不变，持续2个周波；1 s时刻，两换流站分别产生频率为42.1 rad/s、幅值为0.355 p.u.、0.207 p.u.的正弦波动，持续2个周波。观察有功功率波动对直流母线电压的影响。各换流站有功功率和直流电压仿真结果如图13所示。

在图13(b)中，0.1 s时刻发生的功率波动造成的最大直流电压偏差为4.6%；1 s时刻发生的功率波动造成的最大直流电压偏差为5%。与图11(b)对比可知，由于输入波动信号和系统发生了共振，与稳态仿真结果相比，较小的有功功率波动量就使换流站直流电压达到了偏差限制值。

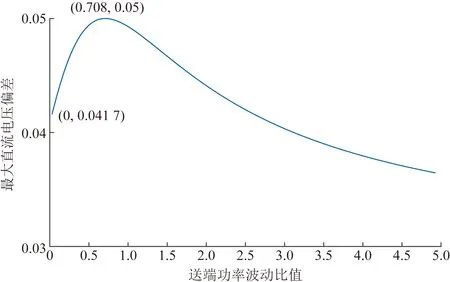
图12 最大直流电压偏差统计Fig.12 Statistic of maximum DC voltage deviation

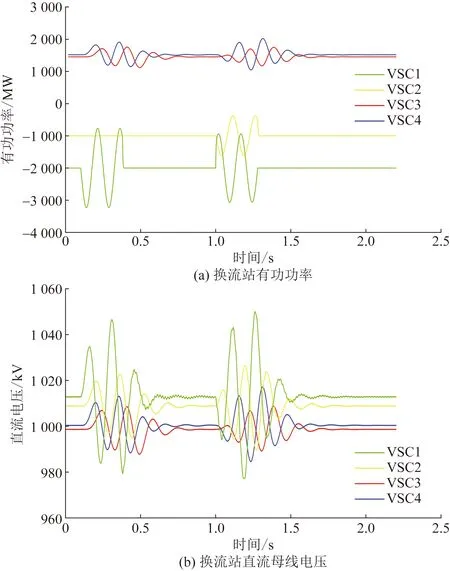
图13 动态分析结果仿真图Fig.13 Simulation diagram of dynamic analysis results

因此，为保证直流电压质量，在规划设计阶段，应根据系统的功率可调节范围和工程技术要求设计系统参数和控制参数；在稳定运行过程中，要结合新能源出力特性，严格按照可调节范围下达功率控制指令；在故障发生时，应充分考虑动态特性对功率波动做出约束，抑制次同步振荡产生或降低其风险，从而为采取储能、弃风弃光、耗能装置投切等相应的输电保障措施提供可能。

4 结论

通过建立多端柔直系统小信号模型，以直流电压偏差为约束，基于奇异值分解和频域分析分别从稳态和动态角度分析了MTDC系统的下垂控制规律，提出了功率可调节范围的量化分析方法，基于Simulink对所提方法进行了算例分析和仿真验证。得出如下结论。

(1)本文方法能够有效量化评估不平衡功率对直流电压质量的影响；送端换流站相较于受端，其直流电压更易受功率波动影响，在控制器设计和系统运行时更应引起注意；对于多输入-多输出的MTDC系统，不同激励方向对应的系统增益不同，应根据奇异值矩阵定量分析系统的不平衡功率调节极限；在某些出力波动的激励下，换流器端口直流电压更容易越过限制值，影响系统安全运行，应采取相应措施抑制其产生或降低其风险。

(2)在后续研究中，可结合小信号模型对MTDC系统进行模态分析，研究各共振峰与特征值的关系，继而优化控制器参数，提升系统性能。