综合能源环境下配电系统的无差异性模式规划问题分析

赵志强， 辛超山， 于志勇， 荆世博， 陈伟伟， 王简

(1. 国网新疆电力有限公司经济技术研究院， 乌鲁木齐 830002； 2.上海交通大学电子信息与电气工程学院， 上海 200240)

随着全球能源紧缺、环境污染等问题日益严峻，各领域均将研究重点放在了如何提升能源的利用率、减少环境污染、保证能源可持续发展上。综合能源系统的提出为解决这一问题提供了一种可行的方案，但与此同时也带来了一定的问题，从配电网规划的角度而言，其复杂性不断增强，主要包括：①多种能源耦合的复杂性：不同类型能源的时间尺度、空间分布及行为模式间均存在异同，如何考虑综合能源环境下系统的成本函数、约束条件等问题均有待进一步的研究[1- 4]；②配电网侧新技术带来的复杂性：主动配电网、微电网等技术在提升供电质量、延缓变电站扩容的同时，不可避免地增加了负荷预测、设备选址定容等方面的复杂性[5- 6]；③优化目标的复杂性：除传统的经济性、安全性目标外，综合能源环境下的配电网规划还关注了低碳性等方面[7]，这些新目标的合理化表征及与传统目标融合等方面均存在复杂性；④模型求解的复杂性：多能耦合下的配网规划通常是一类多目标、多约束、高维度、非线性的随机不确定混合整型组合优化问题，属于难以在多项式时间内验证得出一个正确解的问题 (non-deterministic polynomial-hard problem, NP-hard problem)，求解复杂[8]。

为适应不断增强的复杂性，目前综合能源环境下的规划方法主要有以下特点：①以协同规划思路代替单独规划思路：综合能源环境下的规划强调多种能源之间的耦合协同作用，文献[9]即考虑了多种类型的能源系统在不同环节、不同时空尺度的耦合进行建模，以促进低碳化发展；②以分布式方法代替集中式方法：集中式建模存在计算规模大、时间长等问题，通常适用于传统的单一能源网络，分布式建模可以很好地解决这一问题；③以不确定性方法代替确定性方法。综合能源环境下的不确定性因素日益增多，传统的确定性规划方法已不再适用，随机规划、机会约束规划、鲁棒规划等针对不确定性的规划有利于简化不确定性因素的影响。文献[10]利用马尔科夫链方法对线路气象进行随机模拟，反映线路气象随机性对电网潮流和线路温度的影响。可见，处理综合能源环境下的规划问题，既需要考虑所用方法的适应性，也需要考虑所用方法的可行性、简便性。特别是在如长期规划这一类对准确性要求不高的问题中，规划方法的简便性就更加重要。然而目前所采用的各类简化手法均仅以简化处理能源间的耦合关系及不确定性因素的影响为目的，并不是以简化规划思路为目的。

传统配电网的规划思路，目前也并不是以简化为研究方向，而是以提升规划精细化水平为研究重点，以此提出了差异化规划，主要关注分区可靠性要求及负荷密度的差异性。文献[11]在传统配电网规划模型的基础上，从电网运行可靠性和需求响应两方面，考虑用户的差异化需求，提出了一种配电网资源综合优化配置的方法；文献[12]针对配电网中储能配置的差异化和园区综合能源系统化问题，建立了考虑区域用能平衡、系统投资成本及园区运行经济型三方面问题的三级协同规划方法。这是由于传统配电网规划技术已经十分成熟，有能力进一步向精细化发展，而综合能源环境下的配电网规划则不同，如上文所述，其所处的环境复杂、规划技术不成熟，并且由于综合能源环境下的系统调度模式更丰富，调度能力更强，对规划方面的精确性要求进一步降低。因此，需要简化规划思路，然而目前在该方面的研究几乎为空白。

以差异化规划的思路，进行反向思考，若两区域的负荷密度及供电可靠性要求相同，则规划区内的变压器、线路等设备的性能要求也必然是一致的、可以借鉴的，并以此为基础提出无差异规划方法，即负荷需求(中指密度及供电可靠性)近似相等的分区间设备容量的近似一致性规划。随着综合能源环境下的系统日驱复杂，无差异规划显示出其优越性，为综合能源环境下的规划问题提供了一种简单易行的方法,使各分区的规划具有一定的可复制性。区别于不考虑差异性的配电网规划，配电网无差异规划是一种在考虑差异性基础上忽略次要因素，寻找配网规划一般性的方法。

为此，首先提出了点负荷及面负荷的概念，并基于面负荷的概念，提出了无差异规划的一般性方法，进而结合综合能源环境下变电站、分布式电源及热力系统各主体的行为模式，分析了综合能源环境下的无差异规划，通过算例对无差异性规划的可行性及其在综合能源环境下的应用进行了分析。

1 配电网无差异性模式规划的一般方法

1.1 点负荷与面负荷

提出的配电网无差异规划基于面负荷假设。在一般的电网规划过程中，负荷可以以点负荷(空间负荷)或者面负荷(负荷密度)的方式来表示，面负荷一般以规划区域内的平均负荷密度来表示，是对点负荷的一种简化考虑，相当于假设负荷在规划区内以负荷密度的值平均分布。一般来说，在输电网规划中采取点负荷的方式，而在配电网规划中除特别重要的大用户外，可以只简单地考虑负荷密度，即面负荷问题。基于点负荷的差异性规划与基于面负荷的无差异性规划模型的比较如图1所示。当采取点负荷假设时，需要考虑各负荷的差异特性及网络拓扑结构，因此必须采用差异性规划，规划决策的数学模型较复杂，通常采取启发式的算法。当采取面负荷假设时，可以忽略网络的拓扑结构，在规划区域内采取统一容量、类型或者接线模式的变压器、线路，通过计算变压器和线路的最佳供电半径或者面积确定其分布，极大地简化了规划的复杂程度。

目前中国以分区为单位进行配网规划实际上就是基于面负荷的思想，但这种分区基于地理、行政等环境因素，而且对于负荷的特性也缺少深度的挖掘，更没有明确地提出面负荷的定义。基于面负荷的概念，提出了配电网的无差异规划，是出于一种问题简化的考虑，以损失一定的精确性为代价，换

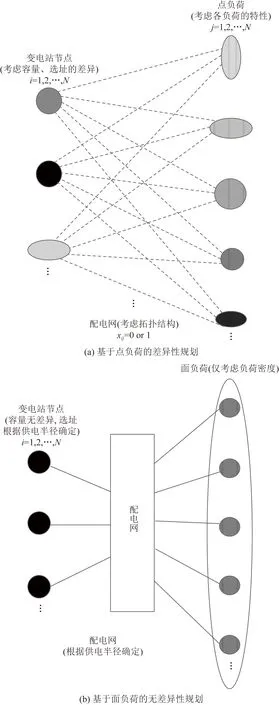
图1 差异性规划与无差异性规划的比较Fig.1 Comparison between discriminate planning and indiscriminate planning

取配电网规划的简化。这一思想在目前配电网日益复杂的环境下具有一定的优势。

1.2 无差异规划模型

在规划问题中，数学计算只是一种辅助决策手段，在模型和计算方法等方面必须考虑一定的简化，例如考虑到基于面负荷假设的条件下，任一供电分区中的变压器总是尽可能保证与负荷在空间及大小上均匀分布，因此可以假设同一供电分区的N台变压器或者线路的容量相同进行规划，再根据实际情况进行微调，即

P1=P2=…=PN=P0

(1)

式(1)中：P1、P2、PN、P0为变压器容量。

不考虑变电站的选址及线路走廊的规划问题。变压器规划通常以规划年内总成本最小为目标函数，总成本包括投资的成本、运行成本、设备折旧成本及电能损耗成本等，以二次函数的形式表示。假设有N0台变压器实际投入使用，则可得混合整数规划模型为

(2)

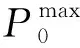
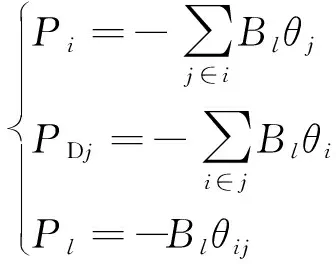
(3)

式(3)中：Pi为发电机节点i的注入功率；PDj为负荷节点j的输出功率；Pl为线路l上的功率；Bl为线路l的电纳；θi、θj、θij为相角。

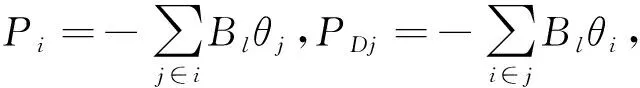
(4)

(5)

式(5)中：N为发电机节点的集合；M为负荷节点的集合。

面负荷假设消除了负荷点的概念，设规划区域面积为A，平均面负荷大小为σ，此处的面负荷是考虑了以供电可靠性要求后的值，对此不做重点考虑，即可以得到G(S0)=0的最终化简形式为

N0P0=Aσ

(6)

1.3 模型的计算

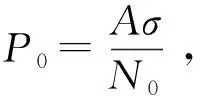
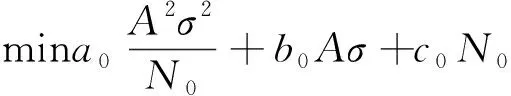
(7)

在误差可以接受的情况下，最优变压器个数及容量为

(8)

即，当

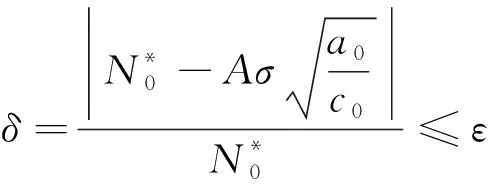
(9)

进一步分析，当误差可忽略时有

(10)

由于配网规划对于精确性的要求不高，在面负荷大小和各变压器及线路的成本函数不变的情况下，可以认为变压器的个数与分区面积的大小成正比。配电网中变压器无差异规划的流程如图2所示。

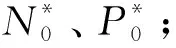
变压器输出的电能均由线路传送至负荷，由于不考虑网络结构，在每台变压器供电半径的限制以

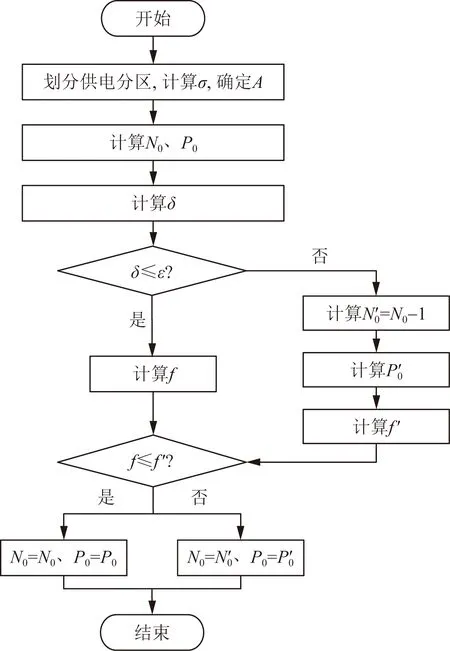
f′为总成本；P′0、N′0分别为减少一台变压器后的变压器个数及变压器最优容量图2 无差异规划流程图Fig.2 Indiscriminate planning flow chart

及变压器和负荷在空间上均匀分布的条件下，可以忽略线路长度不同对投资的影响，而只考虑传输容量与价格的关系，因此传输线路与变压器的规划方法相同,在此不再做详细介绍。仅需要说明由于输电线路的数量通常较大，计算时误差较小，因此比变压器更适合做无差异性规划。

2 综合能源环境下的配电网无差异性模式规划

2.1 综合能源环境下的无差异规划模型

从配电网的角度，考虑分布式电源、热力系统与传统变电站各主体间的耦合关系，对无差异规划进行延拓，建立了综合能源环境下配电网的无差异规划模型，并讨论了各主体行为模式对无差异规划的影响。站在配电系统运营商的角度，以配电系统总成本最低作为优化目标，目标函数可描述为

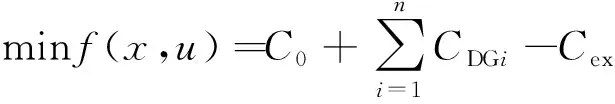
(11)

式(11)中：C0为该情况下变压器的投资；i为分布式电源的类型；CDGi为各类分布式电源的投资；Cex为热力系统应支付给配电系统的补贴，各部分成本可表示为

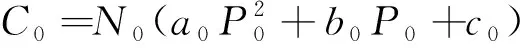
(12)

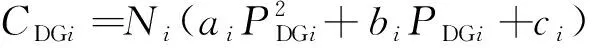
(13)

Cex=k0(β0N0P0)2+k00Pex+

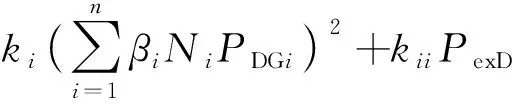
(14)

Pex=γd0N0P0，γ∈[0,1]；d0∈[0,1]

(15)

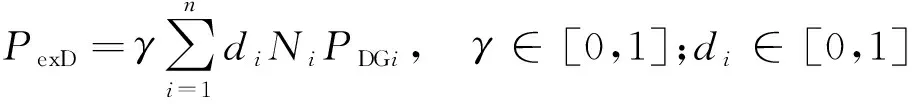
(16)

式中：ai、bi、ci为分布式电源成本函数的系数；i为分布式电源的种类；Ni为每类分布式电源的个数；PDGi为各类分布式电源的出力；β0为传统变电站以电供热的比例；Pex、PexD分别为接受传统变电站、分布式电源余热的热负荷(如供暖系统负荷)能量值；γ为变电站产生的余热与电量的相关程度；d0为变电站余热供热的比例系数；βi为分布式电源以电供热的比例；di为分布式电源余热供热的比例系数；k0为热力系统支付给变电站以电供热的补贴系数；k00为热力系统支付给变电站余热的补贴系数；ki为热力系统支付给分布式电源以电供热的补贴系数；kii为热力系统支付给分布式电源余热的补贴系数。

各主体间的能量流及资金流的交互情况如图3所示，在综合能源环境下，变电站和分布式电源产生的能量可分为两部分，一部分为发电量，另一部分为余热；发电量可以供给电负荷，或供给热负荷，但后一种情况较少；余热可以供给热负荷，或供给本应由电能供给的热负荷，后一种情况也较少；热负荷从属于热力系统，因此当热负荷受到电能的支持时，热力系统应支付给电力系统一定的费用。

变电站、分布式电源产生的总余热的能量值分别用ΔP、ΔPDG表示；ΔL为曾经需要以电供给而现在可由余热供给的负荷(如空调负荷)的电量，则变压器与分布式电源的容量约束可表示为

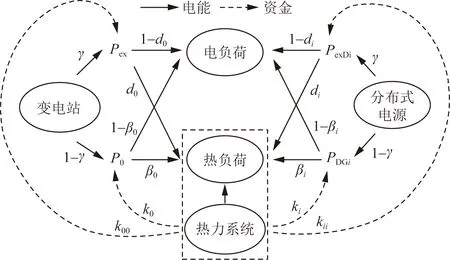
实线表示电能的流动方向；虚线表示资金的流动方向，即一方向另一方支付的费用；线条上方的字母对应能源分配及转换时的比例系数与分配系数图3 综合能源环境下配电网层面的能流交互Fig.3 Energy flow interaction at the distribution network level in an integrated energy environment

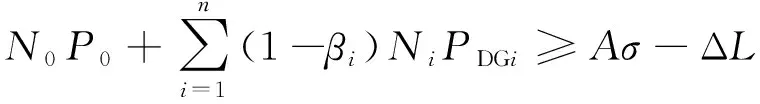
(17)

ΔL=ΔP+ΔPDG-Pex-PexD

(18)

变压器与分布式电源的安全约束为

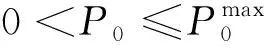
(19)

(20)

变压器及分布式电源数量的整数性约束为

N0=0,1,…,n

(21)

Ni=0,1,…,n

(22)

在各主体的行为模式系数均为确定值时，配电系统的无差异规划显然成立。因此，主要考虑各主体的行为模式对无差异规划的影响。

2.2 各主体的行为模式

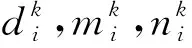
2.2.1 偏好型分布

偏好型分布可以分为供电供热比例相同型偏好、供电型偏好及供热型偏好，可表示为

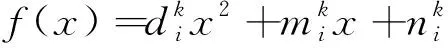
(23)

(1)概率密度的基本性质为

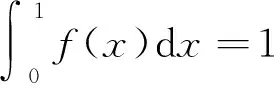
(24)

(2)概率密度的非负性可表示为

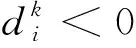
(25)

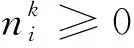
(26)

(27)

(3)概率密度的偏好性质为

(28)

式中：k=1为供电供热比例相同型偏好；k=2为供电型偏好；k=3为供热型偏好。

2.2.2 无偏好型分布

f(x)=1

(29)

传统变电站的行为模式系数为β0、d0。以电供热以高品位能源替代低品位能源，在能源的利用率及环保等方面都具有很大的优势，然而也会给变电站带来增容改造的巨大压力，并且在非供暖季，配电基础设施的运行效率长期偏低，导致投资回收周期过长，甚至无法回收，因此β0应遵循供电偏好型分布。其余热利用的行为模式主要根据可获得收益的多少确定，各种偏好均存在可能。分布式电源的行为模式系数为βi、di，分布与变电站需要遵循的偏好模式基本相同。有所区别的是，βi虽然也遵循用电偏好型分布，但是由于分布式电源的建设规模小、成本低，因此相较于传统变电站而言，其用电偏好模式较为温和。热力系统的行为通过补贴支付系数k0、k00、k1、k11的大小体现，合理的补贴系数能有效激励配电系统以热供电，并提高余热的利用效率。

以仅存在单一类型分布式电源的情况进行分析，获得的结论可以推广至存在多种分布式电源的情况。由于受政策的大力支持，分布式电源规模应设下限，分区的消纳能力限制又使其规模也应设置上限，并以此上下限确定迭代计算的次数及步长。通过无差异规划的思路，可得综合能源环境下的无差异规划计算方法如图4所示。

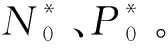
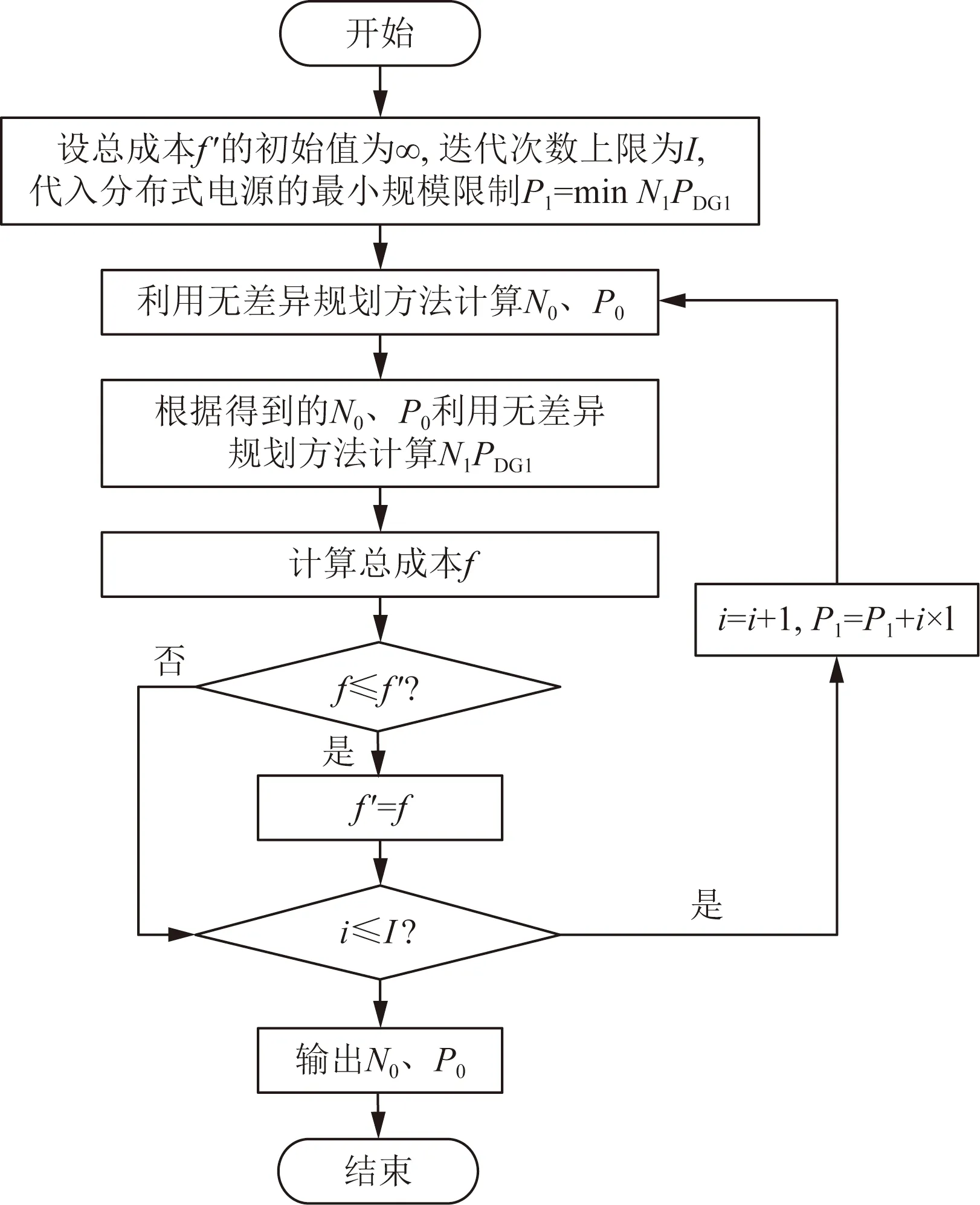
i为迭代次数；l为迭代步长图4 综合能源环境下的无差异规划计算方法Fig.4 Calculation method of indiscriminate planning in integrated energy environment

3 案例分析

对一面负荷为20，面积为30的理想供电分区进行无差异规划，不考虑特殊自然环境、经济情况及社会因素等造成的特殊影响。与变电站、分布式电源、热力系统的成本及行为模式相关的系数如表1所示。分布式电源的初始规模取30，迭代次数为45次、迭代步长为2。分别验证无差异规划的可行性以及从配电系统角度分析传统变电站及分布式电源行为模式对无差异规划的影响。

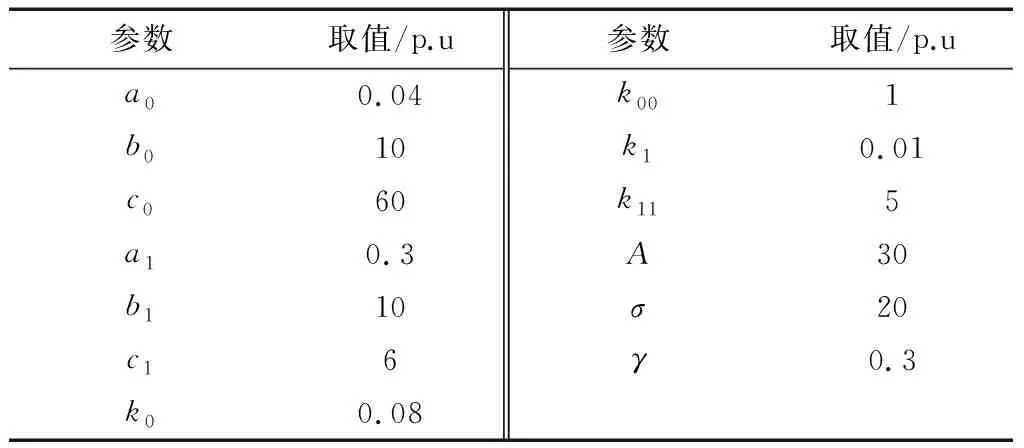
表1 案例所涉及的各系数取值Table 1 Values of coefficients involved in the case

3.1 无差异规划的可行性

针对只存在变电站单个主体的传统配电网进行分析，即与热力系统及分布式电源相关的系数均取0。无差异规划方法强调在负荷密度相同的理想地区中，变电站容量的规划具有可复制性，这一特性可以通过容量相同的变压器，数量与规划区域面积成正比进行表征。因此本例以分区面积大小作为变量，利用无差异规划模型及算法验证其可行性，结果如图5所示。

在各分区面负荷大小相同的情况下，变压器的数量与分区面积大小近似成正比，且分区面积越大、变压器数量越多，所得到的结果准确性越高，变压器容量的大小也越趋于一致。这说明无差异规划适用于分区面积较大，变压器数量较多的分区。或者说，无差异规划更适用于诸如线路一类数量较多的设备的规划中，此时由简化算法带来的相对误差较小。

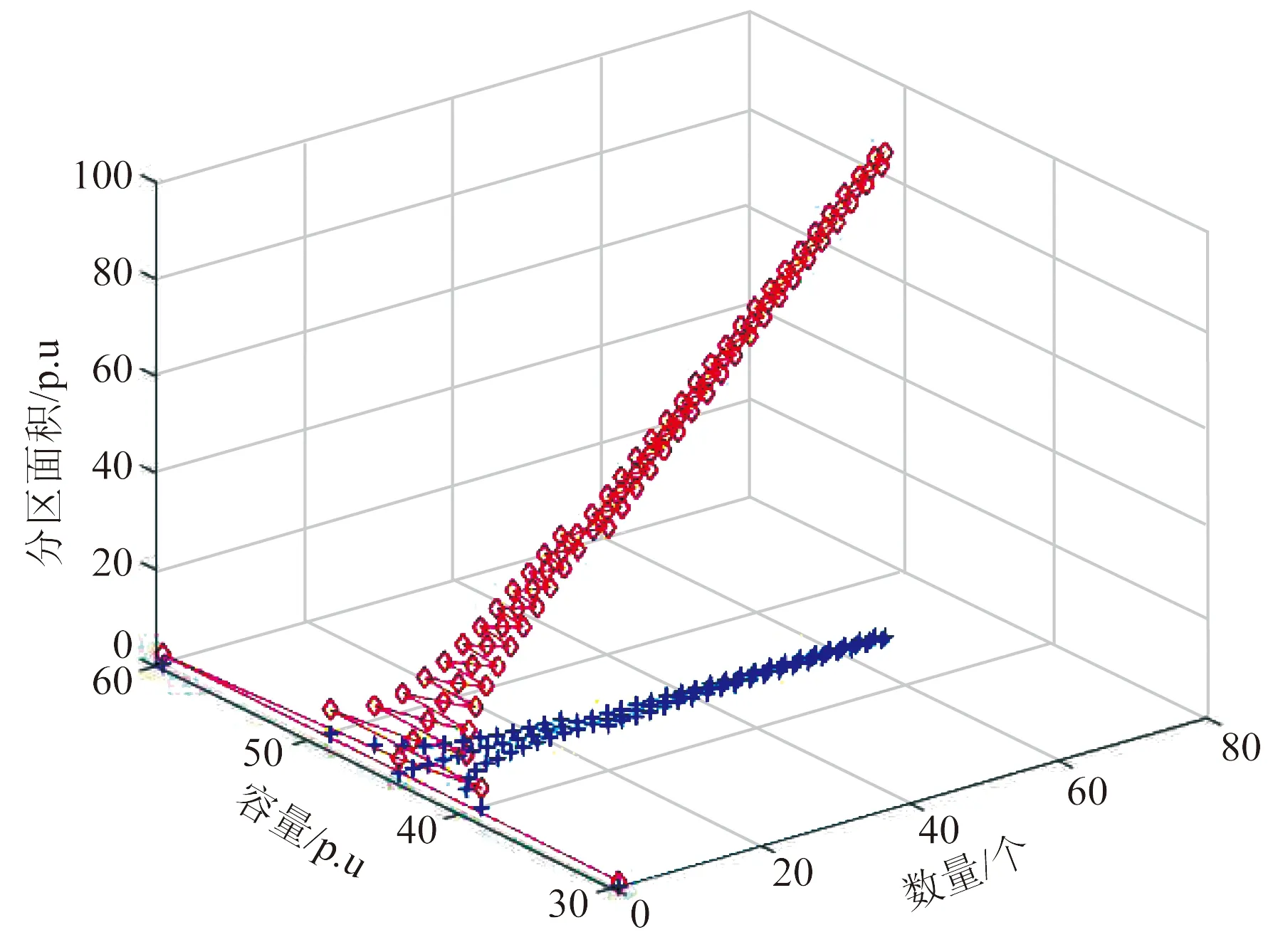
图5 无差异规划的可行性Fig.5 Feasibility of indiscriminate planning planning

3.2 考虑各主体行为模式对无差异规划的影响

规划区域配电网内的传统变电站及分布式电源，均考虑余热利用和以电供热两种行为模式。传统变电站以β0、d0为行为模式变量，β0∈[0,0.3]、d0∈[0,1]，迭代步长分别取0.015、0.05；分布式电源以β1、d1为行为模式变量，β1∈[0,0.3]、d1∈[0,1]，迭代步长分别取0.015、0.05。考虑变电站及分布式电源行为模式下的无差异规划结果如图6所示。

无差异规划能够保证在各主体不同的行为模式下，仍能够将变压器控制在最经济的运行范围内，从而确定相应的变压器数量。通过图6(a)、图6(b)与图6(c)、图6(d)的对比分析可知：传统变电站行为模式的变化对其无差异规划的影响具有很强的规律性，而分布式电源行为模式的变化对配电系统无差异规划的影响却较为复杂。因此在规划前，需要先分析历史数据，并利用预分布式电源的用电偏好。分析可知，由于余热利用的规模较小，且其行为模式不会对配电系统本身的供、用电行为产生影响，仅仅是相当于通过利用余热提高了系统发电的效率，因此其对无差异规划的影响规律性较强。而以电供热的规模较大，且其行为模式影响了各主体的发电规模，所涉及的因素较多，因此其对无差异规划的影响也较为复杂，规律性较弱，需要事先确定其行为模式。

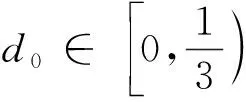
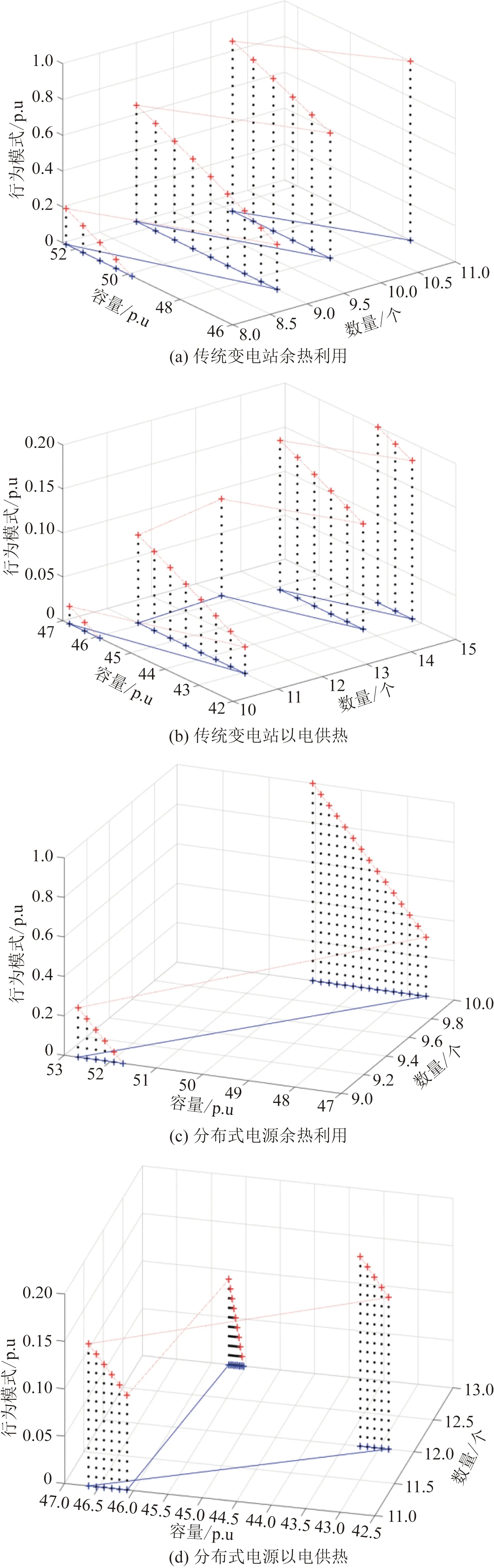
图6 各主体行为模式对无差异规划的影响Fig.6 Influence of the behavior patterns of each subject on the indiscriminate planning

4 结论

所提出的配电网无差异规划是建立在差异性规划思想及面负荷假设基础上的，认为如果几个分区的面负荷大小及可靠性要求相同，则分区中的变压器及线路等设备的容量应该是相同的、可以相互借鉴的，具有一定的可复制性。无差异规划通过对混合整数规划进行简化计算，得到变压器的个数及线路的条数等与供电分区的面积近似成正比关系。在综合能源环境下，各主体均可以选择各自的行为模式，这会对配网的无差异规划产生影响，因此进一步通过算例对传统配电网无差异规划的可行性，及综合能源环境下各主体行为模式对无差异规划的影响进行分析，得出以下结论。

(1)无差异规划更加适用于设备数量较多的情况，如线路容量的规划等，具体数量需根据当地的负荷密度大小确定，后续可以进行进一步的分析。

(2)无差异规划为综合能源环境下的配电网规划提供了一种简化的思想，经验证具有一定的可行性。某地区可以借鉴负荷密度相近地区的变压器容量情况，并根据自身的分区面积大小确定变压器台数。

(3)在综合能源环境下，点负荷密度近似相同的供电分区间，若传统变电站的行为模式或分布式电源余热利用的行为模式不同，无差异规划方法由于其强规律性仍然使用，可以根据实际情况将行为模式系数等分为若干区间，根据自身的行为模式系数所处区间修正无差异规划结果。而分布式电源以电供热的行为模式对无差异规划的影响较为复杂、规律性较弱，因此也不适宜采用无差异规划。