少量已知历史数据下的电能质量复合扰动识别方法

赵晨， 李开成， 张浩毅， 林炜鑫， 曾子莹

(1.福建农林大学机电工程学院， 福州 350002； 2.华中科技大学电气与电子工程学院， 武汉 430074)

电能质量问题近几年引起了科研人员以及工程师的关注，由于电能质量问题增加了电网维护、操作和监测的成本，愈发凸显重要。电能质量问题主要分为：①简单的扰动问题如电压暂降骤升、谐波；②复合扰动：暂降叠加其他扰动或者骤升叠加其他扰动。这些电能质量扰动大大增加了电气设备故障出现的频率。电能质量扰动的检测和识别是一项复杂的工作，扰动波形中包含了有用信息，但不能直接反映扰动类型。正确检测识别这些扰动类型有助于后续采取相应措施，保证无污染的电力供应以及保障设备和人力的安全[1]。

已有的电能质量扰动检测识别实现分成两步，首先对扰动信号进行特征选取，其次对提取的特征进行分类模型的监督学习。这其中特征的选取常用S变换[2]、小波变换[3]和希尔伯特黄变换[4]、经验模态分解[5]等现代信号处理方法。文献[6]提出了一种改进的分段S变换和随机森林结合的识别方法。文献[7]将变分模态分解(variational mode decomposition, VMD)初始化并经过S变换提取的特征通过多重聚类，实现扰动的识别。文献[8]通过扰动在过完备字典上的稀疏表示对扰动进行识别。决策树[9]、支持向量机[10]、极限学习机(extreme learning machine，ELM)[11]等方法则是较常用的扰动分类的机器学习模型。随着深度学习在语音信号处理和图像识别领域取得广泛应用[12]，一些深度网络模型也开始被用于电能质量扰动的自动提取和分类识别。文献[13]提出了一种基于深度卷积神经网络的电能质量扰动检测和分类的全新闭环方法。文献[14]通过训练一个三层深度前馈网络提高扰动识别模型的泛化性和抗噪性。

已有研究工作中扰动分类方法大多采用监督学习的分类模型，即利用已知扰动类型的训练数据训练一个分类器，进而诊断未知的新扰动类型。而在实际应用中，监督学习模型无法将电力系统监测设备保存的无类型标签的扰动波形数据加入模型训练过程中，从而导致过拟合现象。因此，如何有效利用这些未标注样本提升分类器性能成为电能质量扰动识别的热点。针对少量已标注历史数据背景下的扰动识别问题，从机器学习领域的半监督学习出发，提出一种基于混合流形正则化半监督极限学习机的扰动识别方法。首先利用变分模态分解算法提取复合扰动经过分解后的标准能量差作为特征，并将混合了图拉普拉斯和海森正则化的流形学习框架引入极限学习机模型中，最终构建半监督极限学习机模型将已标注扰动和未标注扰动样本一起训练。该方法通过流形正则化约束实现了在复合扰动分类的同时在模型输出空间也保留了数据内部的局部结构，更加有利于最终分类效果的提升。

1 电能质量复合扰动特征提取

1.1 变分模态分解

变分模态分解(variational mode decomposition，VMD)是由Dragomeretskiy等[15]提出的一种新的信号分解方法。它将一个实值信号r(t)分解成k个窄带子信号sk(t)，同时获得每个子信号的中心频率ωk(k=1,2,…,K)。算法通过求解一个受约束的优化问题来获取这些窄带信号及其中心频率ωk，利用调制性质对频谱进行搬移。信号的带宽通过解调信号H高斯平滑度进行估算。算法的约束优化问题可表示为

(1)

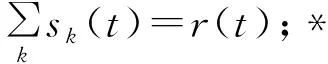
通过拉格朗日乘子λ可以将约束问题转化成无约束问题。扩展的拉格朗日表达式L可表示为

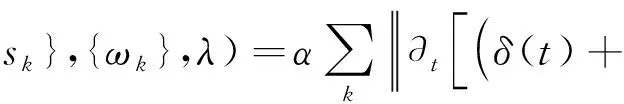
(2)

式(2)中：α为一个惩罚因子;f(t)为原信号。

第n+1次迭代估算的窄带子信号及其中心频率的计算公式为

(3)

(4)

λ的更新可以通过式(5)实现。

(5)

1.2 基于变分模态分解的标准能量差

复合扰动由于多个单一扰动的存在使得特征存在部分重叠， 提出以复合扰动VMD分解的子信号与标准正弦信号VMD分解的子信号之间的能量差作为特征向量。信号分解过程中两个重要的参数：数据保真约束参数α和模式数K对最终分解效果影响较大。考虑到复合扰动的频带范围以及最高谐波次数，将α设置为1 000，K设置为10。

(6)

(7)

式中：Fik为第i个信号的第k个特征值；EMPi(k)为第i个信号的第k层分量的能量；EPure(k)为纯正弦信号进行VMD分解后第k层分量的能量;E(·)(j)为第j个信号能量；Ns为采样点数；ν为计数单元；s(t)为窄带子信号。

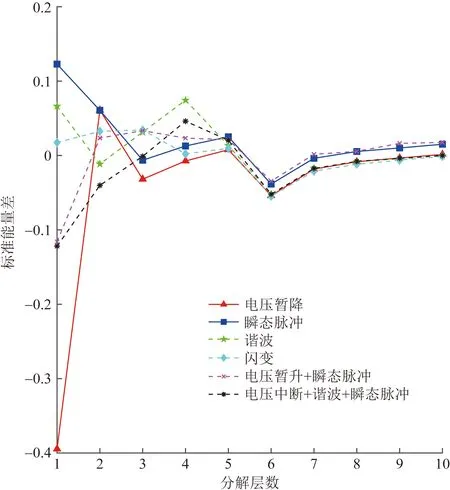
图1 特征提取曲线Fig.1 The curve of the characteristic extraction

图1给出6种类型的扰动信号(电压暂降、瞬态脉冲、谐波、闪变、电压暂升叠加瞬态脉冲、电压中断叠加谐波和瞬态脉冲)经过VMD分解后计算的标准能量差的对比曲线图。由图1可知，标准能量差在6层之前都能较好地体现出不同扰动信号之间的差异性。

2 混合流形正则化极限学习机

2.1 半监督极限学习机

极限学习机作为一种新型的单隐层前馈神经网络因其简单高效而在许多需要使用机器学习的问题上得到了广泛的应用[16]。Huang等[17]提出了一种图拉普拉斯正则化的半监督极限学习机网络模型(semi-supervised extreme learning machine，SS-ELM)。给定一个包含n个训练样本的数据集{X,Y}，其中已标注的样本集为{Xl,Y}l={xi,yi},i=1,2,…,l，其中l为已标注样本个数；未标注的样本集表示为Xu={xu},未标注样本个数u=l+1,l+2,…,n-l，SS-ELM通过在ELM模型目标函数中加入图拉普拉斯正则化挖掘无标签样本中的局部流形信息，从而将监督学习的ELM扩展到半监督学习应用上。其目标函数可表示为

(8)

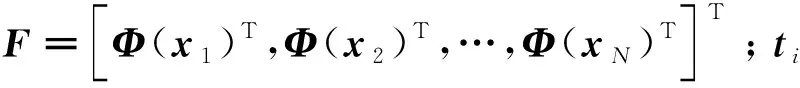
2.2 海森正则化

虽然图拉普拉斯已经在半监督学习中证明有效性，然而它在少量已标注样本较少存在的情况下外推能力较差容易过拟合。由于图拉普拉斯的零空间测地线函数为常数不能很好地保持数据局部流形结构，Kim等[18]提出了在海森流形正则化，使用函数的二阶导数来近似计算每个邻域中的Eells能量。 海森正则化通过在两个方向上近似函数的变化来解决图拉普拉斯外推法的不足。这有助于轻松地识别未被图拉普拉斯正则化惩罚的测地线偏离函数。因此，基于海森正则化的模型比基于图拉普拉斯正则化的模型在训练和测试数据集上具有更好的标签预测能力。

海森正则化中的海森算子H的计算流程如下。

步骤1对于每个样本xi，通过聚类算法K最邻近(K-nearest neighbor，KNN)定义其邻域Nk(xi)，将邻域内每一个样xj均与xi相减，形成最终的矩阵Xi。

步骤2对矩阵Xi做奇异值分解，记Xi=UDVT取左奇异矩阵U前d个特征值所对应的特征向量构成正切空间。

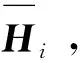
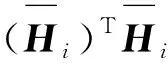
2.3 混合流形正则化极限学习机

图拉普拉斯正则化存在外推能力差的问题，海森正则化也存在流形快速变化情况下海森能量估计不稳定的问题。为了克服两种流形正则化的缺点，提出了结合了图拉普拉斯和海森两种正则化的半监督极限学习机模型图拉普拉斯-海森半监督极限学习机(Laplacian Hessian semi-supervised-extreme learning machine, LHSS-ELM)。LHSS-ELM算法的目标函数参照SS-ELM的框架，通过修改SS-ELM的式(8)获得最终目标函数表达式为

(9)

式(9)中：λ1和λ2为正则化系数。

将约束条件代入目标函数式中重写目标函数为

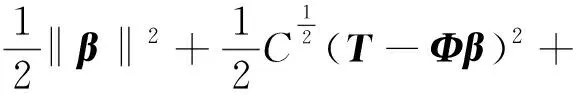
(10)

式(10)中：T=[t1,t2,…,tl]T为训练集真实输出；C为训练误差项对应的惩罚因子。

对β求偏导置0，可得

β*=(Inh+ΦTCΦ+λ1ΦTLΦ+

λ2ΦTHΦ)-1ΦTCT

(11)

式(11)中：Inh为大小为nh的单位矩阵。

当输入样本数少于模型隐层节点数时，有

β*=ΦT(Il+u+CΦΦT+λ1LΦΦT+

λ2HΦΦT)-1CT

(12)

LHSS-ELM算法的具体流程如下。

输入已标注的样本集 {Xl,Yl}={xi,yi}，i=1,2，…,l，未标注样本集Xu={xj}，j=l+1,l+2,…,n-l；惩罚系数C、正则化系数λ1和λ2、隐层节点数。

输出LHSS-ELM的映射函数f:Rd→Rq。

步骤1通过{Xl,Xu}计算图拉普拉斯矩阵L和海森算子H。

步骤2建立一个包含了隐层节点数为nh的ELM网络模型，随机给定输入层权重和偏置。

步骤3计算隐层输出矩阵Φ∈R(l+u)×nh。

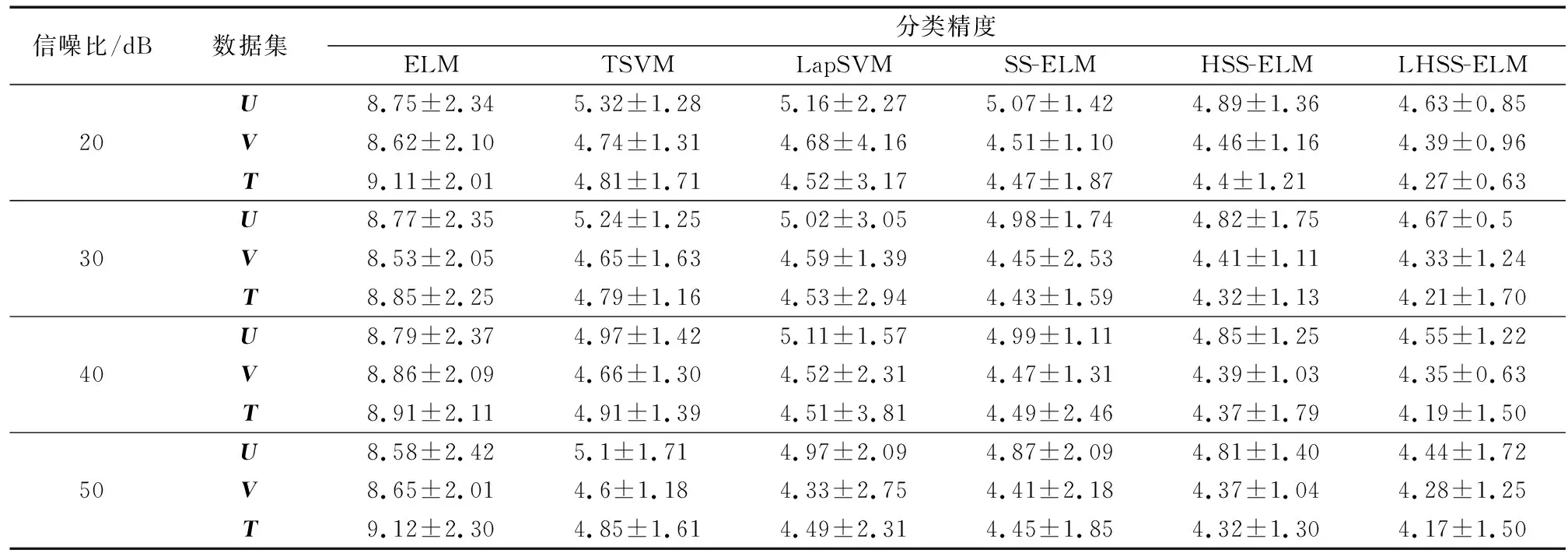
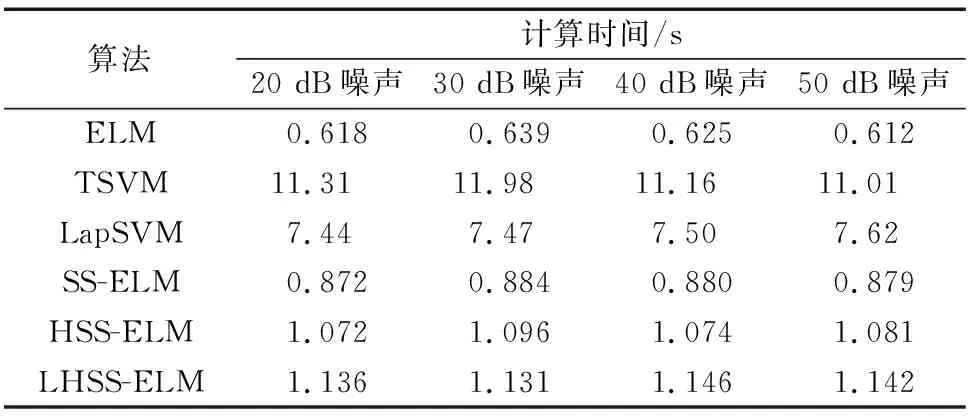
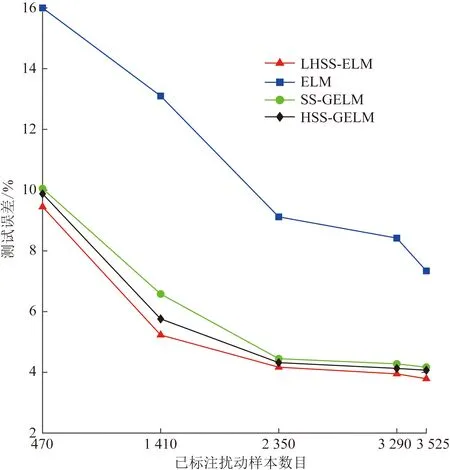
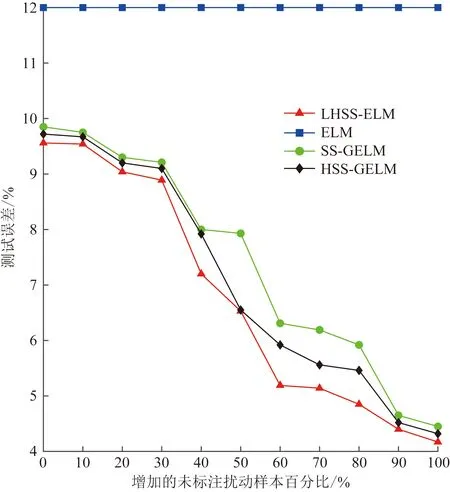
步骤4如果nh

步骤5求得模型映射函数为f(x)=Φ(x)β。

3 实验及结果

3.1 数据集及实验设置

电能质量复合扰动波形数据来源于MATLAB软件数值模型仿真以及福禄克6105A三相功率源的实测数据。其中仿真数据依据参考文献[19]通过MATLAB以6.4 kHz采样频率生成十个周期的波形数据，一共生成47种扰动信号，其中复合扰动信号最多包含4种单一扰动。由于自身限制，标准功率源只能生成15种复合扰动，硬件采样平台如图2所示。最终仿真数据加功率源采样数据一共包含9 400个样本，其中每个类型复合扰动200个样本。实验过程采用四折交叉校验，即四等分数据集，一份用于测试，其余三份用于训练。训练集进一步划分为：已标注集U、验证集V和未标注集T。在20～50 dB的不同噪声环境下，采用4种半监督学习算法：

图2 硬件采样平台Fig.2 Hardware sampling platform

半监督拉普拉斯支持向量机(Laplacian support vector machine，LapSVM)[20]、直推式支持向量机(transductive SVM，TSVM)[21]、半监督极限学习机(semi supervised extreme learning machine，SS-ELM)[18]、海森极限学习机(Hessian semi supervised extreme learning machine，HSS-ELM)[22]和监督学习算法：极限学习机(extreme learning machine，ELM)进行性能对比。以上算法均在Intel I7-6800K 3.5 GHz CPU、32 G内存、Win7系统下MATLAB2020a的环境中运行。

3.2 算法对比结果与分析

表1给出不同噪声条件下，6种算法在复合扰动数据集上性能表现结果。由表1可知，提出的混合流形的半监督极限学习机LHSS-ELM在各项指标上均优于其他方法。与监督学习算法ELM对比，3种流形正则化半监督模型都有较明显的精度提升。结果表明，流形正则化在挖掘未标注数据的信息从而提升分类性能上的有效性。而这其中混合流形方式的半监督极限学习机效果最佳。由表2给出的运行时间结果可见，由于计算了两个流形正则化算子，LHSS-ELM时间消耗最多。

图3给出初始条件为不同数量已标注样本情况下，ELM、SS-ELM、HSS-ELM以及提出的LHSS-ELM在复合扰动数据集上的测试误差趋势。初始状态假定已标注扰动数量为470个，每次递增数量为样本总数的10%，增加过程保持校验集与已标注集样本数量相同。由图3可见，随着已标注样本数量增多4种方法的测试误差均趋于减少，其中LHSS-ELM测试误差最低。而比例增长到一定值后，4种方法误差降低趋势均有所放缓。图4给出固定已标注样本数目情况下，以未标注样本总数10%的数量往训练集添加未标注样本时，4种算法的测试误差趋势变化曲线。分析可知，随着未标注样本数量的增加，LHSS-ELM测试误差呈明显下降趋势，且在4种

表1 不同信噪比下算法分类精度对比Table 1 Comparison of classification accuracy for algorithms under different SNR values

表2 不同信噪比下算法计算时间对比Table 2 Comparison of computational cost for algorithms under different SNR values

图3 已标注样本数目不同时测试误差对比Fig.3 Comparison of testing error with different number of labeled data

方法中最低。即使在初始阶段训练集未添加任何未标注样本的情况下，LHSS-ELM测试误差也在4个方法中最低。这其中主要原因是由于流形正则化在纯监督学习的情况下也具有有效性。

图4 未标注样本数目不同时测试误差对比Fig.4 Comparison of testing error with different number of unlabeled data

4 结论

针对电网实测复合扰动样本多数未标注类别而无法加入监督学习模型训练的情况，提出了一种新型的基于混合流形正则化的LHSS-ELM半监督扰动识别模型。本文算法通过图拉普拉斯和海森流形正则化的结合，利用未标注样本蕴含的局部结构信息来降低全部标注未知样本的代价。结果表明，混合流形正则化的引入有效提升了复合扰动半监督学习精度，与单一的图拉普拉斯和海森正则化对比具有更好的局部几何结构保持和外推能力。实验结果证明所提方法是一种有效的从半监督学习角度识别复合扰动的新方法，具有广阔的应用前景。