基于蝙蝠与粒子群混合优化算法的光伏MPPT研究

黄荣赓，陈路遥

(厦门理工学院光电与通信工程学院，福建厦门 361024)

现今光伏发电已成为全球最主要的可再生能源发电方式之一。由于光伏组件的输出特性曲线是受光照强度、温度与负载等影响的非线性曲线，为了提高电能转化效率，就需要采用最大功率点追踪(maximum power point tracking,MPPT)技术，使组件工作在最大功率点。但在实际的应用中，当出现局部遮荫的情况，由多块光伏组件串联而成的光伏阵列P-U曲线就会出现多个峰值点。传统的扰动观察法[1]、增量电导法[2]等MPPT 算法就容易失效。针对此问题，研究人员提出了一些新颖算法，例如人工神经网络算法[3]、遗传算法[4]、蚁群优化算法[5-6]、蝠鲼优化算法[7]、粒子群优化算法[8-9](particle swarm optimization,PSO)等。人工神经网络算法运算速度较快，效率高，但需要大量数据和时间训练，否则易陷入局部峰值点。遗传算法能够使光伏系统稳定运行在最大功率点，但容易早熟并且收敛速度慢。蚁群优化算法能够在遮荫条件下搜索到最大功率点但收敛速度偏慢。蝠鲼优化算法具有良好的鲁棒性并能有效地追踪全局最大功率点，但算法较复杂。粒子群算法具有全局搜索能力，搜索精度高，易于计算，并且容易在商用控制器上实现，但算法的搜索速度较慢。蝙蝠算法(bat algorithm，BA)是一种新型的群智能算法，具有全局搜索能力，前期收敛效果好，但后期搜索速度慢，容易产生搜索偏差。

针对蝙蝠算法和粒子群算法的不足之处，本文提出了一种基于蝙蝠与粒子群混合优化(bat and particle swarm hybrid optimization,BPSHO)的MPPT 算法。在混合算法的前期，采用BA，提升算法收敛速度，在算法中后期，采用PSO，提升搜索精度。在前期的BA 中引入PSO 的惯性权重和社会学习因子，避免BA 收敛精度低和早熟收敛的缺陷，在中期运行PSO的过程中引入BA 的局部搜索机制，并采用指数方程调节混合算法的参数，在保证搜索精度基础上，进一步提升搜索速度。

1 在局部遮荫条件下光伏阵列的特性

在实际应用中，为了满足负载对光伏系统电压和电流的需求，光伏组件通过串并联的方式连接形成光伏阵列，当光伏阵列中的部分光伏组件被云层、建筑和树等物体遮荫，这些组件的光照强度就会弱于未被遮荫的组件。为了避免热斑效应出现，旁路二极管将被遮荫的组件旁路，将导致光伏阵列的P-U曲线出现多峰值的情况。以3×1 光伏阵列为例，3×1 光伏阵列由三个光伏组件串联而成。在如表1 所示的三种光照条件下，光伏阵列的I-U曲线和P-U曲线如图1 和图2所示。

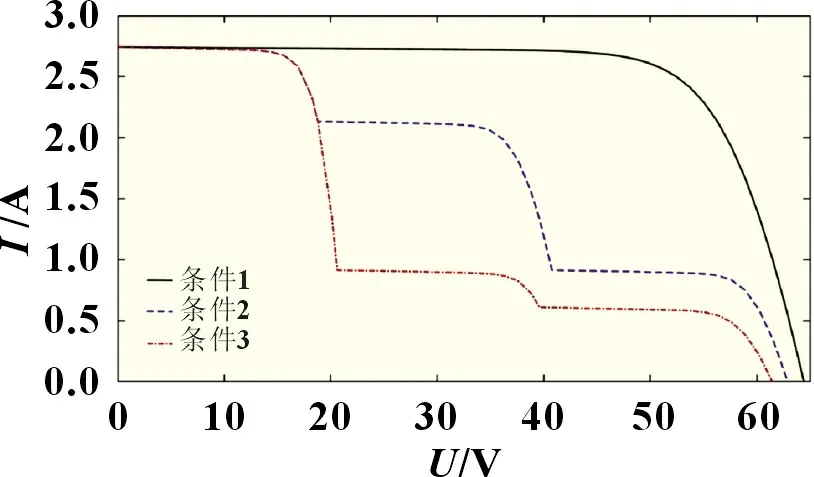
图1 光伏阵列的I-U曲线

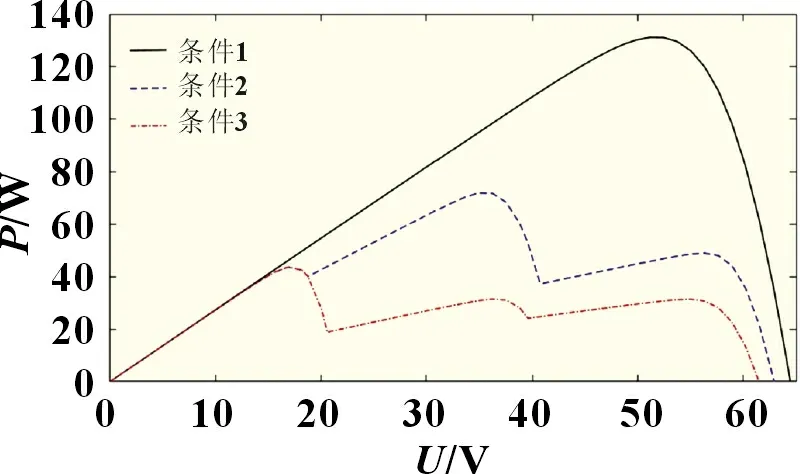
图2 光伏阵列的P-U 曲线

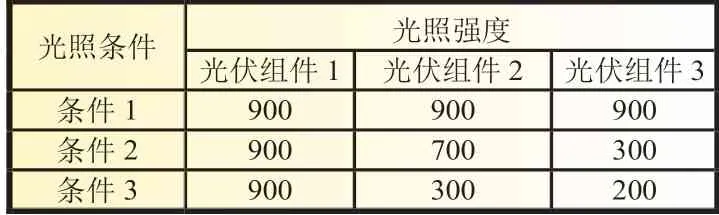
表1 光伏阵列的光照条件 W/m2

从图2 所示可知，在均匀光照条件下(条件1)，P-U曲线只有一个峰值，在局部遮荫条件下，即光伏组件接受不同光照强度时(条件2、3)，P-U曲线出现多个峰值。不同的遮荫形式会导致不同的峰值个数和全局峰值功率点(GMPP)出现在不同的电压区域。这种现象将大幅度降低传统MPPT 算法追踪最大功率点的有效性。

2 粒子群算法和蝙蝠算法原理

2.1 粒子群算法

1995 年，Kennedy 和Eberhart 提出了PSO 算法[10]。算法中粒子的位置是问题的可行解，每一次的演化，粒子依据自身的飞行惯性，并通过追踪粒子本身找到的历史最优解和整个群体目前所找到最优解更新自身速度和位置，最终靠近或找到全局最优解。速度和位置更新采用式(1)和(2)：

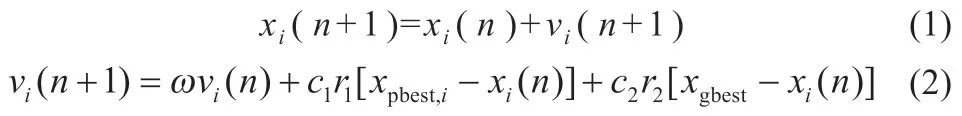
式中：xi为粒子i的位置；vi为粒子i的速度；n为迭代次数；ω 为惯性权重；r1和r2为在[0,1]之间的随机数；c1为认知学习因子；c2为社会学习因子；xpbest,i为第i个粒子历史最佳位置；xgbest为所有粒子的最佳位置。

2.2 蝙蝠算法

蝙蝠算法(BA)是由Yang[11]于2010 年提出的一种模拟自然界蝙蝠捕猎和避障行为的随机搜索算法。在BA 中，蝙蝠的位置即为问题的可行解，k只蝙蝠在可行解的空间中飞行，蝙蝠的频率、飞行速度和位置更新公式如式(3)～(5)：

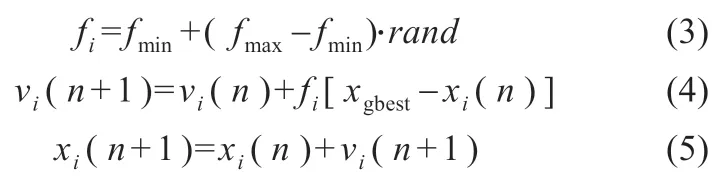
式中：fi为蝙蝠发出超声波的频率；xi为蝙蝠i的位置；vi为蝙蝠i的速度；n为迭代次数；fmin和fmax为超声波的最小和最大频率；rand为在[0,1]之间均匀分布的随机数；xgbest为所有蝙蝠的最佳位置。

对于局部搜索，生成一个随机变量rand1，如果rand1 大于此时超声波脉冲频率ri(n)，蝙蝠就会在最佳位置附近游走，按照式(6)更新蝙蝠位置：

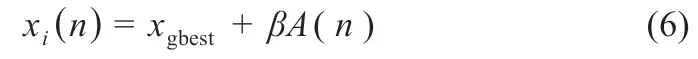
式中：A(n)为蝙蝠群体在第n次迭代的平均响度；β 为[－1,1]之间的随机数。超声波最初响度较高，最初脉冲频度较低，如果它在飞行的过程中发现猎物，则会逐渐降低响度，同时逐渐增加频度。脉冲频度和响度更新规则如下：

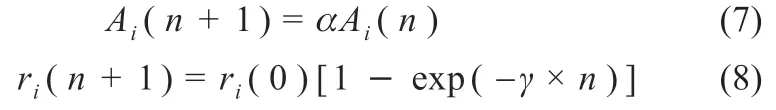
式中：Ai(n)和ri(n)为蝙蝠i在第n次迭代的响度和脉冲频度；ri(0)为蝙蝠i的最初脉冲频度；α 和γ为常数。

3 粒子群与蝙蝠混合优化算法(BPSHO)

3.1 BPSHO 算法的基本思路

PSO 能够实现在全局搜索最大功率点，搜索偏差小，但收敛时间较长，而BA 也具有全局搜索功能，前期搜索速度快，但后期搜索时间长，搜索精度低。鉴于这两种算法的特点，结合两种算法在搜索不同时期的优势，BA 应用于混合算法前期，提升前期的搜索效果，PSO 应用于算法中后期，提升算法的搜索精度，并分别对两种算法进行改进。

3.2 前期蝙蝠算法的改进

蝙蝠的速度更新式(4)的第一部分和粒子群的速度更新式(2)的第一部分均为上代个体速度项，粒子群可以通过惯性权重ω 调节个体惯性对速度的影响，为了平衡混合算法前期的全局搜索能力和后期的局部搜索能力，在前期蝙蝠算法中引入中后期PSO 的ω。蝙蝠的速度更新式(4)的第二部分和粒子群的速度更新式(2)的第三部分都为群体认知项，蝙蝠是通过频率而粒子是通过社会学习因子c2调节群体经验对速度的影响，两者可以共用参数c2。为了进一步提升收敛速度，ω和c2会随着迭代次数而改变，因此改进后蝙蝠算法的速度更新式为：

在BPSHO 算法早期，为了保证蝙蝠的多样性和较强的全局搜索能力，提高搜索精度，应选择较大的ω 和较小的c2，在后期为了加快粒子收敛速度，减小ω，增大c2。按照指数规律调节ω 和c2，如式(10)和(11)所示：

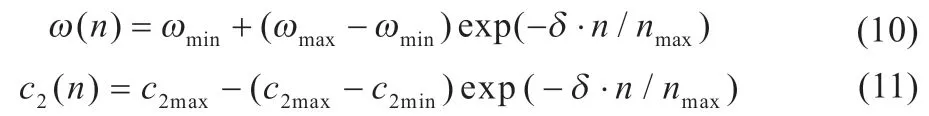
式中：ωmax和ωmin为惯性权重的上下限；c2max和c2min为社会学习因子的上下限；ωmax和c2min也是惯性权重和社会学习因子的初始值；nmax为最大迭代次数；δ 为参数调节系数，通过调节δ改变ω 和c2的变化速度。

3.3 中后期PSO 算法的改进

中后期的PSO 与前期BA 共用ω 和c2，并且认知学习因子c1也设置为迭代次数的变量，PSO 算法的速度更新式改为：

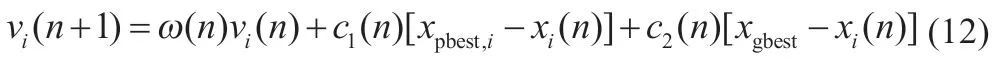
粒子通过c1调节个体历史经验对速度的影响，为了保证中期的粒子多样性并减少搜索时间，c1按照指数规律减小，参数变化规律如式(13)所示：

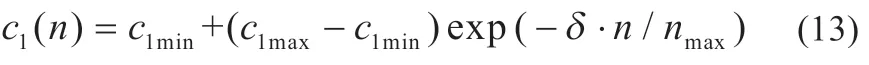
式中：c1max和c1min为认知学习因子的上限和下限。

为了进一步提升搜索速度，在PSO 中期继续保留前期蝙蝠算法的局部搜索机制，满足触发条件，粒子会从其它位置直接跳跃到现有的最佳位置附近，但此时粒子可能保留较高的速度，粒子就容易在下一次迭代中越过最佳工作点所在的区域，降低搜索性能。因此在局部搜索后的下一次速度更新中，引入惯性衰减系数ε，减小惯性对速度的影响，ε 的取值范围为(0,1)，速度更新公式调整为：

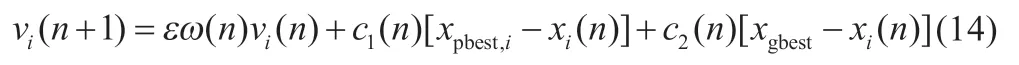
3.4 用于光伏系统MPPT 的BPSHO 算法描述

实现BPSHO 算法的PV 系统由3×1 光电阵列、boost 变换器、BPSHO 算法控制器等组成。系统通过BPSHO 算法控制器输出占空比D，控制升压变换器调节光伏阵列的输出电压和电流，实现最大功率追踪。

混合算法的流程如图3 所示。

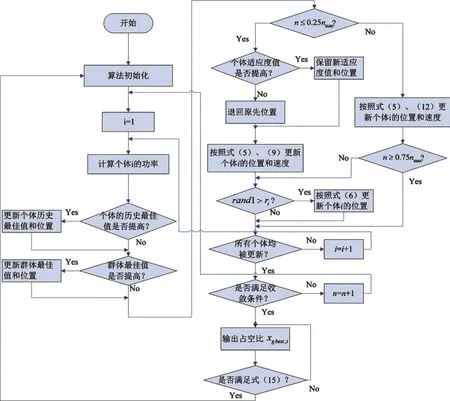
图3 BPSHO算法流程图

具体步骤如下：

步骤1：选择参数，以Boost 电路开关管的占空比D为个体位置，光伏阵列的输出功率为个体适应值。个体数目k与串联的光伏组件数目相同。设置响度衰减系数α、脉冲频率增强系数γ，脉冲最初频度ri(0)，脉冲最初响度Ai(0)，惯性权重的上限ωmax和下限ωmin，认知学习因子的上限c1max和下限c1min，社会学习因子的上限c2max和下限c2min，最大迭代次数nmax，个体移动的最大速度vmax。

步骤2：初始化种群，在搜索空间[Dmin,Dmax]中均匀放置k只个体。个体从初始位置Di以初始速度vi出发。

步骤3：控制器输出占空比，等到Boost 变换器稳定后，得到功率作为适应度值，如果个体i的适应度值优于它的历史最佳值，更新个体最佳值和相应位置。如果个体i的适应度值优于所有个体的最佳值，更新群体最佳值和相应位置。

步骤4：如果迭代次数n＜0.25nmax，即处于算法前期，按照BA 的式(5)和式(9)更新个体的速度和位置，ω 和c2按照指数式(10)和(11)调整。并且启用局部搜索机制产生一个随机数rand1，如果rand1＞ri，则根据式(6)在最优位置附近产生新位置。

步骤5：如果迭代次数n＞0.25nmax，按照PSO 的式(5)和式(12)更新个体的速度和位置，ω、c1和c2按照指数式(10)、(11)和(13)调整。在算法的中期，即0.25nmax＜n＜0.75nmax，继续采用局部搜索机制，如果局部搜索产生新位置，下一次速度按照式(14)更新，在算法后期，即n≥0.75nmax，取消局部搜索机制，利用PSO 自身的特点保证局部的搜索深度和收敛速度。

步骤6：确定收敛条件，如果迭代次数达到最大收敛次数或所有个体的速度小于某个限值，算法结束，控制器输出的占空比即为群体的最佳位置xgbest。

步骤7：当外部环境或负载发生变化时，全局最大功率和它相对应的电压会发生改变，因此系统重新初始化种群搜索全局最大功率点。判断条件如式(15)所示：

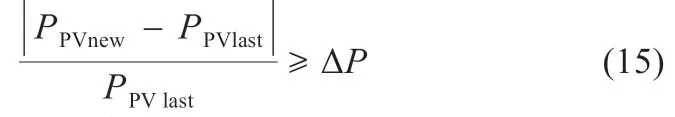
4 仿真与实验结果分析

为了分析BPSHO 的精度和追踪速度，搭建光伏系统仿真模型和实验电路。光伏系统包括3×1 光伏阵列、Boost 电路、BPSHO 控制器和负载电阻。单个光伏组件的参数：最大功率Pmax=50 W，最大功率点电流Ir=2.78 A，最大功率点电压Ur=18 V，短路电流Isc=3.05 A，开路电压Uoc=21.6 V，Boost 电路参数为：C1=100 μF，C2=150 μF，L=1 mH，PWM 载波频率f=20 kHz，系统采样周期为0.05 s，算法个体数目k=3。

4.1 仿真与结果分析

在MATLAB/Simulink 平台中建立光伏系统仿真模型，模型如图4 所示。在局部遮荫条件下，分别用PSO 和BPSHO 进行光伏阵列最大输出功率追踪。PSO 采用线性方式调节ω，c1和c2[9]。两种算法基本参数一致。

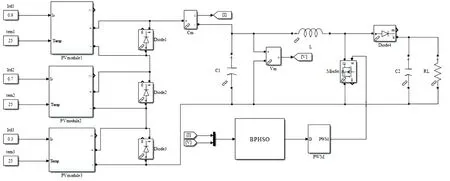
图4 光伏系统仿真模型

表1 所示的光照条件2 和3 分别对应不同的遮荫环境，两种条件下最大功率点出现在P-U曲线的不同区域。在条件2和条件3 下，最大功率点的功率分别为72.925 和44.268 W。PSO 与BPSHO 的光伏阵列输出功率曲线如图5 和图6 所示。在条件2 与条件3 下，PSO 算法追踪过程的迭代次数分别为14 和17 次，追踪时间分别为2.10 和2.55 s，迭代结束后，功率收敛值为72.915 与44.262 W。在条件2 与条件3 下，BPSHO的迭代次数分别为7 和10 次，追踪时间分别为1.05 和1.50 s，功率收敛值为72.922 和44.263 W。

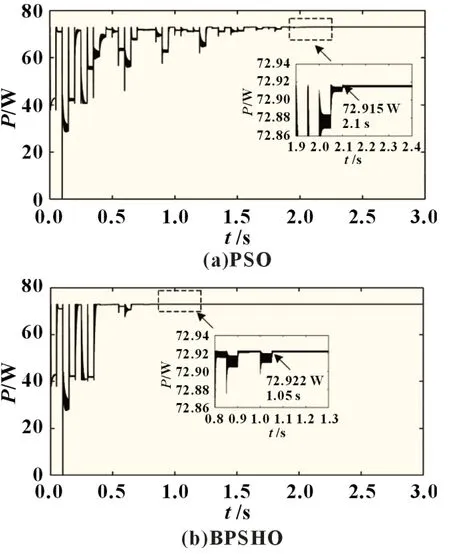
图5 光照条件2下的光伏阵列功率追踪波形图

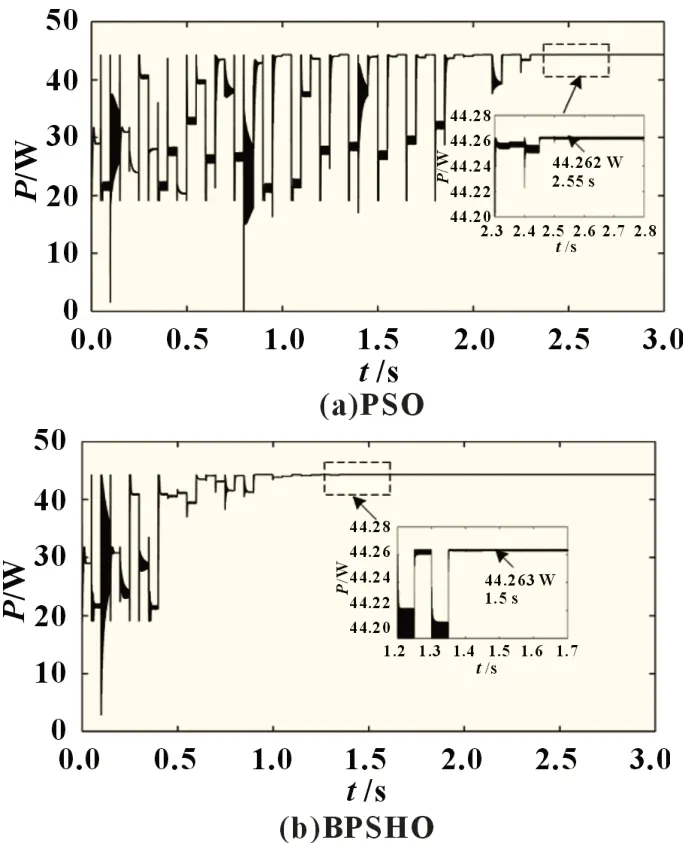
图6 光照条件3下的光伏阵列功率追踪波形图

从功率收敛值可看出，局部遮荫条件下PSO 与BPSHO都能有效追踪最大功率点。PSO 与BPSHO 平均追踪时间分别为2.325 与1.275 s。BPSHO 的用时仅为PSO 的54.8%。BPSHO 有效缩短了最大功率的追踪时间。

4.2 实验与结果分析

实验电路中的BPSHO 控制器以STM32103C8T6 为主控芯片，以滑线变阻器作为负载电阻，光伏组件和Boost 电路参数已经在前文中提及。

实验时用半透明纸对光伏组件进行遮荫，一块光伏组件上放置2 张半透明纸，另一块光伏组件上放置6 张纸，最后一块不被遮荫。分别用PSO 和BPSHO 进行MPPT，光伏阵列的输出电压U和输出功率P的波形如图7 所示。从图7 可看出，PSO 追踪GMPP 所需的时间为2.55 s，而BPSHO 所需的时间仅为1.2 s，是PSO 的47.06%。

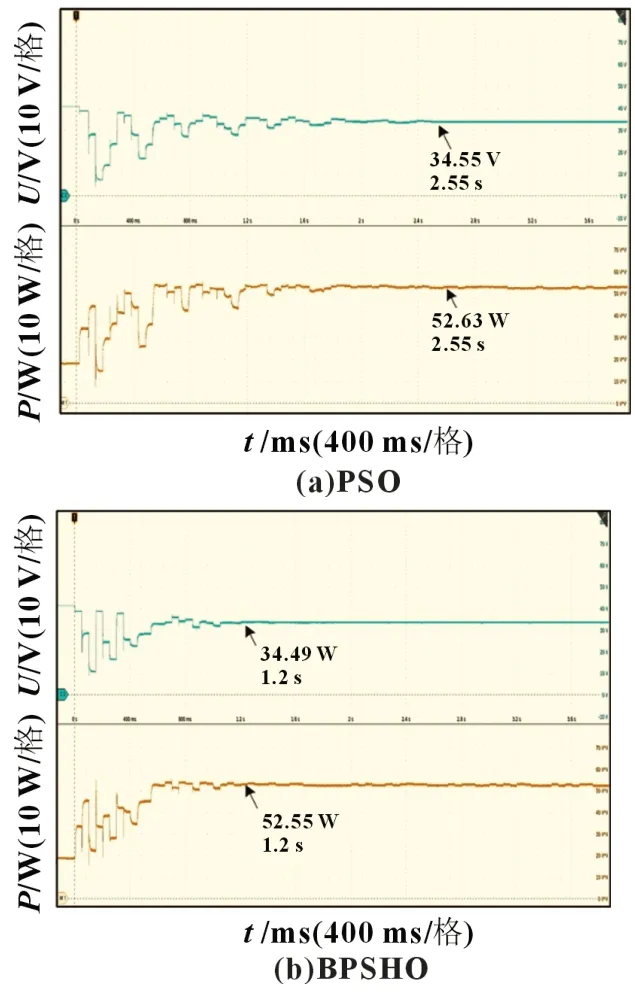
图7 光伏阵列的实测电压和功率波形图

5 结论

针对在局部遮荫条件下群智能算法追踪最大功率点速度较慢的问题，引入BA，提出了基于BPSHO 的MPPT 算法。该算法前期采用BA，中后期采用PSO，运用指数方程调节混合算法的参数，并在中期运行PSO 的过程中加入局部搜索机制。仿真与实验结果表明：BPSHO 算法相较于PSO，能够在保证实现GMPP 准确追踪的前提下，追踪时间只有PSO 的一半左右。