基于特征迁移的光伏功率短期预测

杜仲耀，陈晓英，邓 宇，孙丽颖

(辽宁工业大学电气工程学院，辽宁锦州 121001)

随着大规模具有不确定性的光伏发电机组接入电网，电力系统调度运行的难度也在不断增加[1]。2020 年12 月我国发布IEC 首个可再生能源功率预测国际标准——《可再生能源发电功率预测》(IEC TR 63043:2020)，标志着可靠的光伏发电功率预测(PVPF)将成为智能电网建设至关重要的组成部分。

由于受太阳运动、环境条件、季节变化和地理位置等因素影响，光伏发电功率会有很大波动，融合深度学习建模和时间相关原理的日前光伏功率预测可以解决传统人工智能方法对复杂非线性系统存在过拟合、泛化能力差的弊端[2]。由于深度学习对大量历史数据的依赖性，在新建光伏电站数据不足的情况下，预测模型无法满足调度机构对预测精度的要求。

针对上述问题，本文研究日辐照度特征分析，引入t-SNE流形学习对气象数据进行特征提取，构建基于日辐照度特征、光伏电池温度、气象数据特征的预测模型特征矩阵；建立迁移学习的GRU 神经网络，使用长期运行电站的历史数据作为源域数据集进行预测模型预训练，以新建光伏电站少量运行数据作为任务域数据集，对光伏电站出力预测模型微调，实现预测模型本地化。

1 光伏功率预测特征构建

光伏发电系统输出功率受太阳辐照度、环境温度、湿度等气象因素的影响，面向太阳能资源的气象数据集可为光伏功率预测提供多种可靠的数据支撑。由于太阳辐照度是影响光伏电站发电功率最重要的因素，精确地识别辐照度的数据特征对于时间序列的预测至关重要[3]。另一方面，气象数据维数过高会增加预测特征的识别难度[4]。为降低历史数据复杂度，本文构建包括日辐照度特征、光伏电池温度和气象数据特征的预测特征矩阵F。

1.1 日辐照度特征

根据太阳辐照度随天气和季节变化波动的特点[5]，在预测模型预训练和迁移学习过程中，使用天气特征系数ME、季节特征系数SE和C.V日离散系数提取总辐照度GHI 数据特征，实现对源域和任务域数据的日辐照度特征辅助识别功能。

1.1.1 天气特征系数

天气特征系数描述的是预测日实际辐照度与理想辐照度的相关性，该系数越小辐照度受当前工况气象因素影响越明显，实际辐照度波动性越强。天气特征系数ME如式(1)所示：

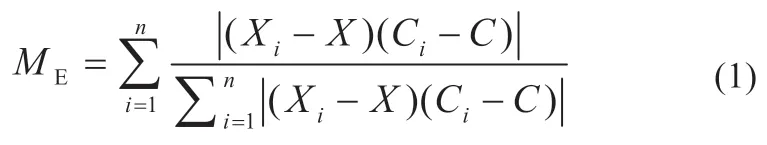
式中：Xi为当日第i时刻实际辐照度；X为当日平均实际辐照度；Ci为当日第i时刻实际辐照度；C为当日平均理想辐照度，理想辐照度根据“晴空模型”计算[6]。

1.1.2 季节特征系数

季节特征系数对季节变化进行量化，该系数越大越接近下一季节。季节特性系数SE如式(2)所示：

式中：Ni为不同季节平均辐照度等级，将不同季节平均辐照度从小到大分别取1 到4 级；Cimax为当前季节理想最大辐照度。

1.1.3 日离散系数

为对不同日辐照度时间序列离散程度进行区别，采用离散系数进行度量而不是常见的标准差。离散系数C.V即标准差与平均值的比值，如式(3)所示：

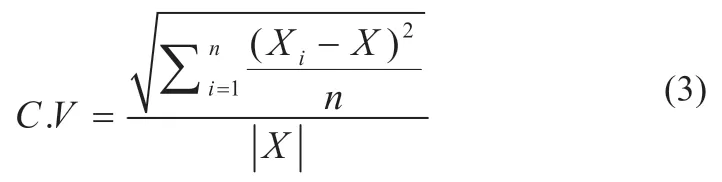
1.2 光伏电池温度

光伏电池温度的物理模型将神经网络的特征识别简化[7]，最大程度地发挥弱相关变量作用的同时降低了输入变量复杂性。光伏电池组件温度τ 如式(4)所示：)

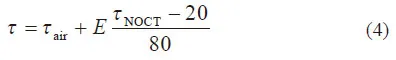
式中：τ 为光伏电池组件温度，℃；τair为环境温度，℃；τNOCT为标称工作电池温度，℃，在20 ℃，800 W/m2下确定；E为环境温度下的辐照度，W/m2，此处视为总辐射GHI。

1.3 气象数据特征提取

对于处理非线性强、弱相关变量多的问题[8]，对光伏电站历史运行数据使用t 分布随机近邻嵌入(t-SNE)算法[9]进行特征提取，通过降低数据特征复杂性，提高预测模型对数据特征的识别能力。t-SNE 算法提取气象数据特征的具体步骤如下：

(1)设n个高维系统运行数据集合S={x1,x2,…,xn}，高维空间的数据点两两之间服从高斯分布，描述高斯中心相似的条件概率为Gj|i，如式(5)所示：

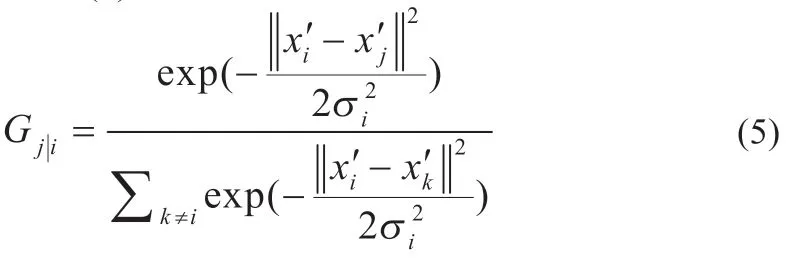
式中：σi为数据点xi的高斯分布方差。

(2)根据式(5)计算空间中任意两个数据点的联合概率分布Gij，如式(6)所示：

(3)设T={α1,α2,…,αm}为集合S在低维空间中服从自由度为l的t 分布的映射，则系统运行数据任意两个特征矩阵联合概率分布Qij，如式(7)所示：

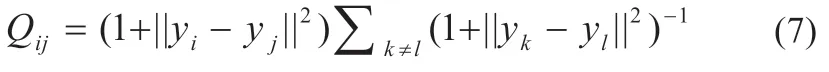
(4)t-SNE 将映射正确性用Kullback-Leibler 离散度DKL表示，如式(8)所示：

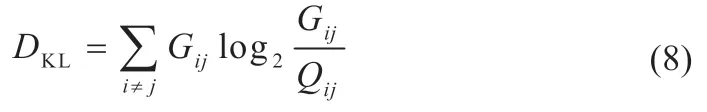
(5)利用梯度下降法迭代求最小离散度，使气象特征矩阵T正确率最高。设最大迭代次数为S，则基于t-SNE 算法对高维数据区分数据特征的流程，如图1 所示。

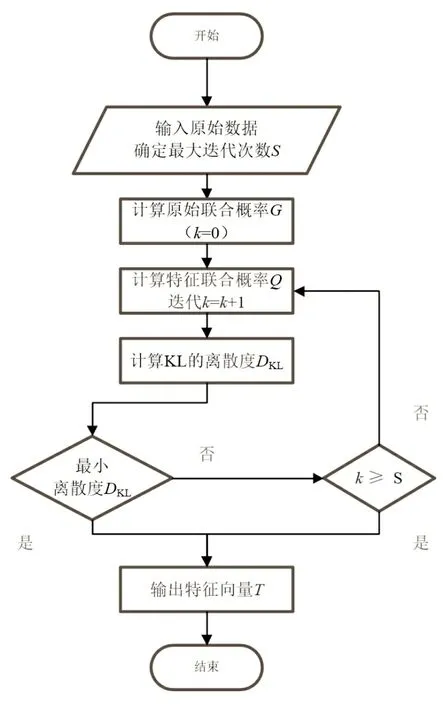
图1 利用t-SNE算法进行高维数据降维流程

2 预测模型建立

2.1 门控循环单元模型

长短期记忆神经网络(LSTM)作为时间序列预测领域最受关注的方案，由于其模块参数多、结构复杂、计算速度慢且处理大数据问题容易过拟合。门控循环单元(GRU)[9]只有更新门和重置门，保持LSTM 基本性能的同时具有更简单结构，这在大数据预测领域具有重要意义。GRU 单元结构如图2所示。

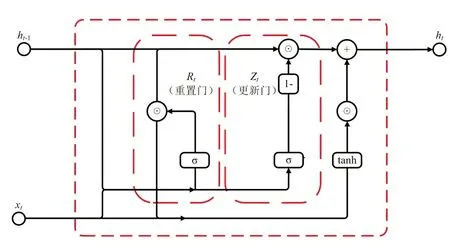
图2 门控循环单元结构

GRU 单元传递方程如下：

令Zt为t时刻GRU 的更新门，Rt为t时刻GRU 的重置门，如式(9)和(10)所示：

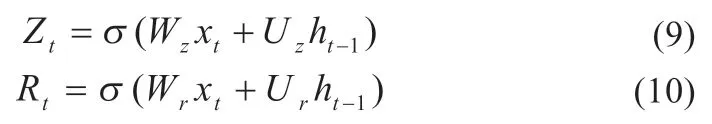
式中：σ 为激励函数Sigmoid；Xt和ht-1分别为当前时刻输入和上一时刻隐藏状态；Wr为输入权重矩阵；Ur为回路连接的权重矩阵。

令ht为t时刻GRU 的当前隐藏状态，如式(11)所示：

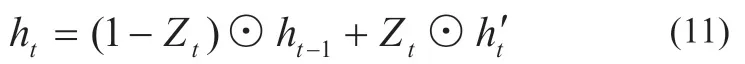
式中：⊙表示Hadamard 积。

上一时刻隐藏状态ht′如式(12)所示：

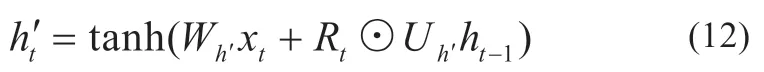
式中：tanh 为双曲正切函数。

综上所述，当更新门Zt=0 时完全遗忘上一时刻状态，当Zt=1 时不再学习新数据，即更新门的激活控制神经网络的长时期记忆能力。当Rt=0 时只与当前输入有关，当Rt=1 时失去遗忘能力，即重置门的频繁激活来控制短期记忆能力。

2.2 迁移学习的GRU 神经网络

为解决新建光伏电站本地数据(目标任务域)DT匮乏的问题，使用迁移学习将长期运行的光伏电站历史数据(源域)DS对新建电站预测模型预训练，本地数据完成预测模型的微调，克服了传统机器学习需满足相同数据分布的问题。迁移学习的GRU 神经网络(TL-GRU)结构如图3 所示。

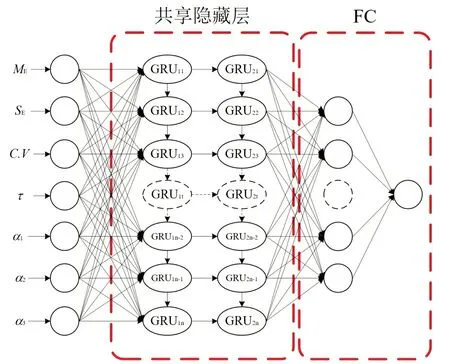
图3 迁移学习的神经网络结构

GRU 神经网络的迁移学习主要分为2 个阶段：

(1)模型预训练。基于TL-GRU 的预测模型，由1 个输入层、2 个隐藏层和2 个全连接层(FC)组成；随机初始化输入权重和阈值；使用源域进行预训练，产生初始网络中隐藏状态ht并在源域和目标域之间共享。

(2)迁移学习。在预训练的神经网络基础上，根据目标域对FC 层进行微调(Fine-tune)以限制迁移学习过拟合[10]，完成模型本地化。基于TL-GRU 的预测输出Pt如式(13)所示：

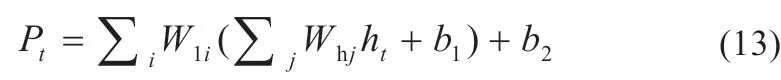
式中：Pt为目标任务域中预测发电功率；Whj为隐藏层与第一层FC 的权重矩阵；W1i为第一层FC 与输出层的权重矩阵；b1为第一层FC 的偏置量；b2为输出层的偏置量。

3 光伏功率短期预测实现

3.1 预测算法流程

本文研究的特征提取和迁移学习的GRU 神经网络预测模型(FTL-GRU)具体实现步骤总结，基于特征迁移的光伏发电功率短期预测流程如图4 所示。

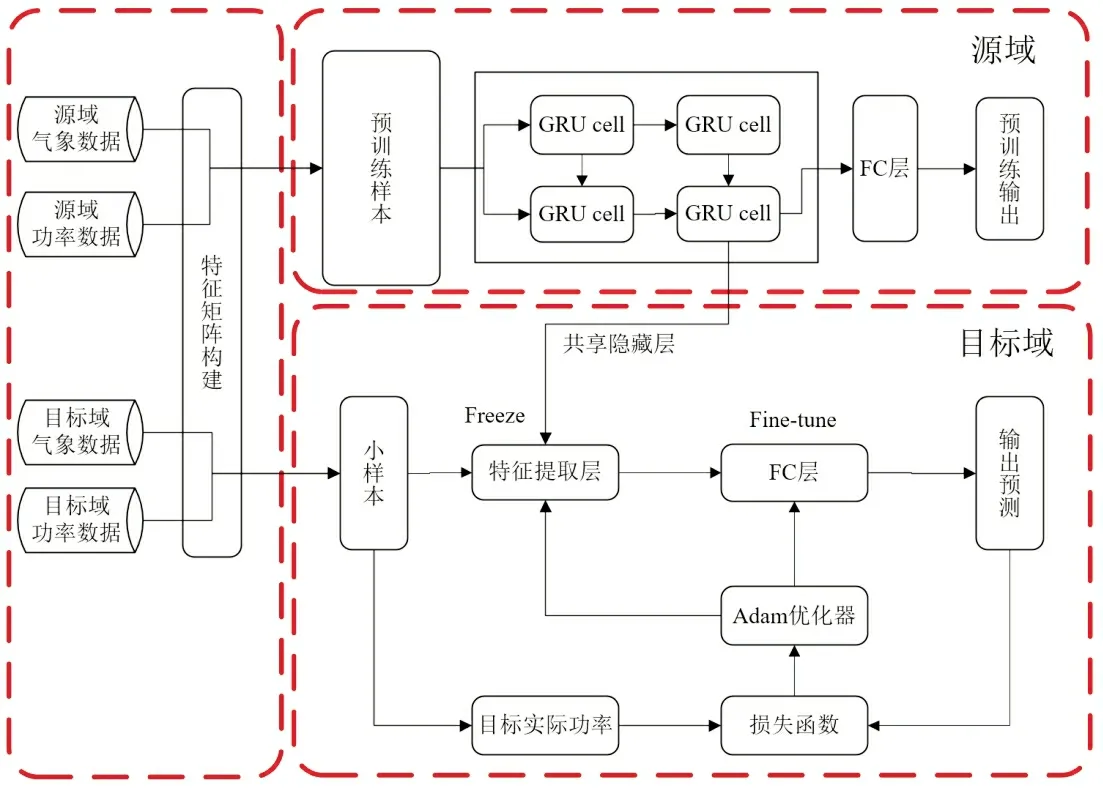
图4 光伏电站出力预测模型

基于特征迁移的光伏功率短期预测具体步骤如下：

(1)模型特征构建：根据式(1)～(4)计算太阳辐照度的日天气特征ME、季节特征SE、日离散系数C.V和光伏电池组件温度τ；将气象数据使用t-SNE 算法进行特征提取，得到气象特征矩阵T以提取源域和任务域公共特征。综上确定基于特征迁移的GRU 神经网络预测模型的输入特征矩阵F,如式(14)所示：

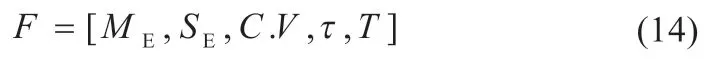
(2)训练样本选取：源任务特征集FS作为预训练数据集。

(3)预训练模型：根据FS对预测模型进行预训练，学习率设置为0.9；建立基于迁移学习的GRU 神经网络。

(4)迁移学习样本选取：根据目标特征集FT对预训练预测模型进行迁移学习。

(5)参数微调：根据式(13)对GRU 神经网络参数进行微调，学习率设置为0.01。

(6)功率预测：使用自适应矩估计(Adam)作为求解优化器，根据标准化输出与实际功率计算损失函数MSE，利用完成迁移学习的预测模型，根据未来24 h 数值天气预报数据，预测未来24 h 光伏发电功率。

3.2 预测可靠性评估

光伏电站出力预测误差对于评估模型的预测精度至关重要，本文选用NRMSE和NMAPE作为光伏功率预测评价指标，如式(15)(16)所示：

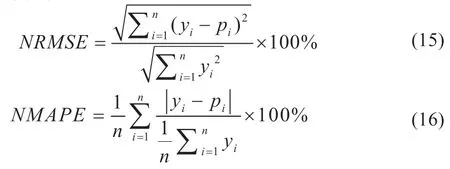
式中：yi和pi为光伏功率的实际测量值和相应的预测值。

4 预测仿真与分析

为验证基于FTL-GRU 的光伏功率短期预测模型性能，首先选用DKA 太阳能研究中心数据作为DS[11]共35 136 个数据点366 d，使用我国中部某光伏电站历史数据为DT共2 880 个数据点30 d。时间分辨率为15 min，预测时间为日前24 h，预测数据集DP⊂DT共96 个数据点，代码编辑器采用PyCharm。

4.1 数据预处理

为消除变量间数量级差异对神经网络学习增益的影响，将数据归一化，以保持发电功率与各变量之间的相关性。除发电功率外其他变量均使用一般归一化公式，标准发电功率PNormal如式(17)所示：

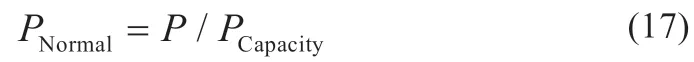
式中：P为功率值；PCapacity为当前在线光伏装机容量。辐照度过低而功率倒灌时P为0。

4.2 实验结果分析

为量化t-SNE 算法特征提取的性能，引入Spearman 相关性系数对气象特征矩阵T与原始数据S=DS∪DT各向量相关性进行比较。原始数据S包括：光伏电站实际发电功率(Power)、风速(WS)、环境温度(WT)、环境湿度(WRH)、地面水平辐照度(GHI)、散射辐照度(DHI)、风向(WD)、和日降水量(WDR)共8 个向量。

将传统主成分分析(PCA)和t-SNE 算法特征提取能力进行比较，如表1 所示。

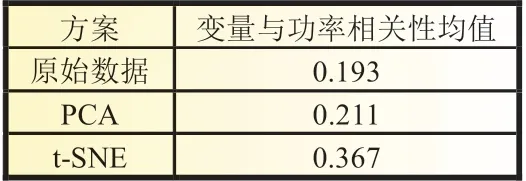
表1 特征提取能力对比

由表1 可知，与原始数据相比，特征提取后各变量与功率的相关性明显加强，且t-SNE 算法性能明显优于PCA。t-SNE算法所构建特征矩阵T和原始数据各变量相关性系数如表2。

表2 相关性系数

在原始数据S 中，GHI 与发电功率相关性系数为0.991，对功率具有决定性作用，其他因素相关性不明显且变量较多，不利于神经网络预测模型的特征识别。气象特征矩阵T各向量与功率输出相关性分别为－0.498、0.582 和0.641，均呈现强相关且复杂性更低。

为精确对比预测性能，本文将特征迁移的GRU 神经网络预测模型(FTL-GRU)与其他预测模型进行比较，如图5 所示。

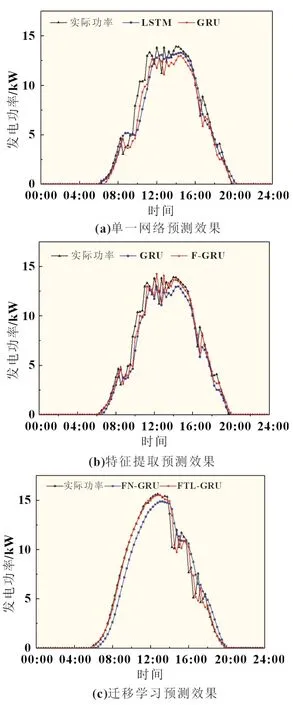
图5 各预测模型对照

其中，LSTM 和GRU 模型表示使用DS对神经网络进行训练及预测；F-GRU 模型表示使用FS对GRU 网络训练及预测；FN-GRU 模型表示使用FS完成训练并对DP进行预测。

由图5(a)和表3 可知，相比于LSTM，由于GRU 神经网络结构较为简单，在处理光伏功率预测这类复杂问题时，能够对数据波动特征更精准地捕捉。

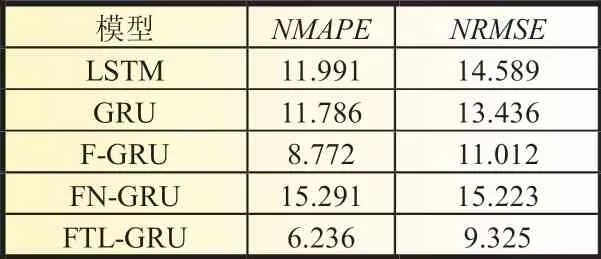
表3 不同模型性能指标对比 %

GRU 与F-GRU 模型进行比较如图5(b)，F-GRU 预测精度NMAPE为8.772%，NRMSE为11.012%，均优于单独的GRU 网络模型。据此可知，建立特征矩阵能有效提高预测模型的特征识别精度，提高预测性能。

FN-GRU 模型的NMAPE为15.291%，NRMSE为15.223%，预测精度和稳定性都低于其他模型。这表明，直接使用其他光伏电站预测模型用于DP的预测任务，其泛化能力不足以满足预测要求。

如图5(c)及表3 所示，本文所研究的FTL-GRU 预测模型，NMAPE为6.236%，NRMSE为9.325%。迁移学习的预测模型能够在缺乏历史数据的新任务上微调预训练的网络，预测模型具有较好的适应能力。不同预测模型可靠性误差如表3 所示。

5 结论

本文使用日辐照度特征、光伏电池温度和t-SNE 算法对气象数据进行特征提取，构建光伏功率预测特征矩阵。相比于直接输入光伏电站历史运行数据，构建预测特征矩阵F可以更好地捕捉气象特征，降低数据复杂度以提升模型对高维数据特征的识别能力。为解决新建光伏电站时神经网络预测模型所需训练数据不足的问题，采用迁移学习对GRU 神经网络进行训练，使用长期运行光伏电站数据完成预训练，少量新建光伏电站数据对预训练模型进行微调，完成预测模型本地化。仿真结果表明，采用该方案的新建光伏电站预测精度与基于本地大数据的预测模型精度相当，达到预训练模型本地化的目标，为调度机构提供可靠信息。