整数规划方法在物流运输管理成本优化中的应用研究

文/王守方

随着互联网的发展，电商行业在国内得到蓬勃发展，物流是助力电商行业发展的重要环节，尤其对某电商平台采用自营采销的商业模式来讲，实现物流运输的供销平衡时，如何分配运输商品，实现物流运输成本最低显得尤为重要。本文针对一项具体的供销平衡问题，利用整数规划方法研究如何实现不同供应地和需求地的调运问题，使得总运输成本最少。

1.引言

近年来，随着进入我国经济的高速发展的新时代，电子商务和物流行业应运而生并且发展迅猛，电子商务与物流行业的关系密不可分，一方面电子商务刺激着传统货物运输模式的改变，另一方面物流行业给了电子商务新的运营思路[1]。我国物流行业起步晚，基础弱，发展相对滞后，物流成本控制体系还不完善，尤其在在电商行业，较大的物流成本已经成为电商企业的发展负担。如何合理的安排物流运输、控制物流运输成本，成为电商企业财务管理的主要目标。对自营采销的电商而言，供销平衡是最理想的状态，在该状态下，可以避免库存成本和短缺成本。供销平衡是生产数量与销售数量相等，使市场商品供应量及其构成与市场上货币支付能力的商品需求量及其构成之间保持平衡。供销平衡运输问题是生产数量和销售数量相等的运输问题。对于电商平台而言，如何合理地根据市场需求以及运输成本调配不同供应生产地生产相等数量的产品显得极其重要。针对物流运输中遇到的成本优化问题，可以运用运筹学中的整数规划建立数学规划模型，并利用excel作为求解工具，方便快捷的寻找出成本最低方案。

2.整数规划数学模型的建立

2.1 商品物流运输方案的选择目标

整数规划问题是带整数变量的最优化问题，即在受约束于一组等式或不等式约束条件下最大化或最小化一个全部或部分变量为整数的多元函数的最优化问题。整数规划是数学规划的重要部分，许多经济、管理、交通、通信和工程中的最优化问题都可以用整数规划来建模[2]。对于电商平台而言，在运输路线单位成本既定的情况下，如何合理的根据市场需求以及运输成本调配不同供应生产地的商品到需求地使得综合运输成本最低。实际上供应产品的分配是一种指派问题，其目的是安排Ai地产品通过合理分配到By地并使总成本达到最优（即所需物流运输成本最少），也称为分配或配置问题，是关于资源合理配置或最优配置的问题[3]。

2.2 线性约束条件

在产品分配运输数量时，需要考虑以下几个因素：

2.2.1 供应产地（或供应商）的约束条件

该约束条件主要是假设某一产品在所有可能供应商可供应的总和。

2.2.2 需求地（或销地）的约束条件

该约束条件主要是假设某一产品在所有需求地所需求产品数量的总和。

2.2.3 产品被分配的数量约束条件

该约束条件主要是假设某一产品运到各销地的数量为非负整数。

2.3 模型的建立

基于以上分析假设，可以建立以下针对优化运量分配方案的整数规划模型：设xij表示由供应产地i运输到j销地的数量，且xij满足以下条件。

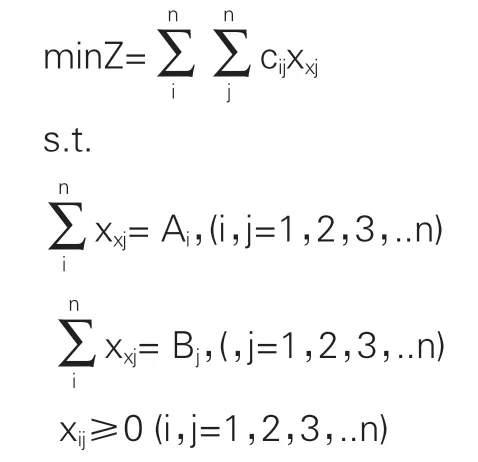
其中，cij为由供应产地i运输到j销地的单位运输成本，成本矩阵为C=(cij)n×n。

2.4 模型求解方法

Excel是微软公司的办公软件Microsoft office的主要组成部分。它具有数据处理、统计分析和模型求解等数据分析和处理功能，被广泛地应用于企业管理、经济统计、金融等诸多领域[5]。Excel中的规划求解宏主要用来解决整数规划与非整数规划中的优化问题。本文为解决工作分配管理问题建立的数学模型正是运用Excel表中的规划求解加载项以及SUMPRODUCT函数，可以直接一键求出最优解。具体计算步骤：

第一步：在excel表格中建立任务分配量化模型，即将效率矩阵C=(cij)n×n、决策变量矩阵xij；约束条件、目标函数值等信息设置在一张表格中；

第二步：在目标函数值表格中设置SUMPRODUCT([array1]，[array2]，[array3]，...)函数；

第三步：加载“规划求解”加载项。具体加载步骤：首先从Microsoft Excel“文件”菜单中找出“选项”命令，将会弹出Excel选项对话框，然后在对话框左侧点击加载项，此时右侧会出现查看和管理Microsoft Excel加载项对话框，此对话框底部有“转到(G)…”选项，点击后出现“加载项”对话框。选择“规划求解”并单击“确定”按钮进行加载，加载完成后“规划求解”处于菜单“数据”栏中。

第四步：在已安装“规划求解”的Microsoft Excel菜单“数据”栏中右上方，选择“规划求解”，弹出规划求解参数设置对话框，分别设置目标单元格、目标函数类型（最大值、最小值或者设置等于某一值）、设置可变单元格、添加约束条件、无约束变量非负数设定、选择求解方法。点击“选项”按钮，还可以对规划求解进行高级设置。所有参数设置完成后，点击“求解”按钮，即可计算出最优解。

3.模型应用实例

假设某电商平台的某种商品的供应产地有三个A1、A2、A3，需求地区有四个B1、B2、B3、B4，目前供销商品数量均为120件，其中供应产地A1、A2、A3供应数量分别为28、54、38；需求地区B1、B2、B3、B4需求数量分别为44、26、24、26。下面探讨供销平衡状态下如何进行商品运输分配才能使运输成本最低。

商品由Ai运输到Bj地的单位运输成本为Cij，单位运输成本矩阵如表1所示。

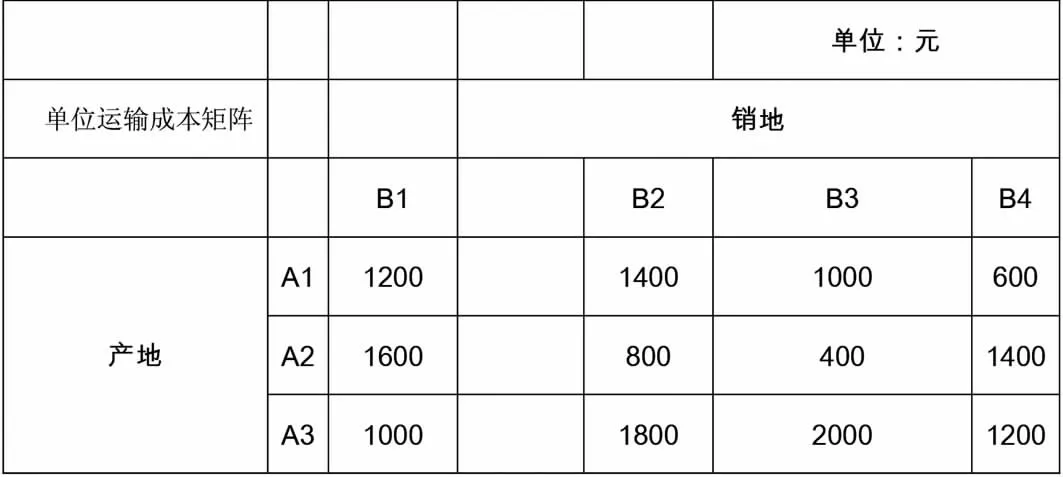
表1 单位运输成本矩阵

3.1 运用excel进行求解

完成整数规划建模后，利用Excel整数规划方法确定最优的采购任务分配方案。

3.1.1 在excel表格中建立运输分配量化模型

函数目标为使运输成本最低，成本分配矩阵、约束条件与总成本计算设置格式可按照表2进行。其中，单位运输成本矩阵（$C$3:$F$7）已知，决策变量矩阵（$C$11:$F$13）初始值设为0，另需要构建约束行或列，最后构建目标函数单元格$C$16

表2 成本分配矩阵、约束条件与总成本计算设置

3.1.2 设置目标函数以及添加整数规划约束条件公式

在目标函数单元格C16中输入函数SUMPRODUCT(C3:F7，C11:F13)。

在构建好的约束行或者列表格中设置约束条件公式

在Excel表格中设置供应地约束公式：H11=G11=SUM(C11:F11)=28、H12=G12=SUM(C12:F12)=54、H13=G13=SUM(C13:F13)=38；需求地约束公式：C15=C14=SUM(C11:C13)=44、D15=D14=SUM(D11:D13)=26、E15=E14=SUM(E11:E13)=24、F15=F14=SUM(F11:F13)=26。

3.1.3 加载“规划求解”加载项并进行规划求解参数设置

打开规划求解参数设置对话框后，依次设置目标单元格“$G$12”；目标函数类型勾选“最小值”；设置可变单元格“$C$11:$F$13”；逐项添加约束条件（$C$11:$F$13≥0、$C$14:$F$14=$C$15:$F$15、$G$11:$G$13=$H$11:$H$13）；勾选“使无约束变量为非负数”；选择求解方法中的“单纯整数规划”；最后点击“求解”即可。

3.1.3 对目标函数进行求解

运用Excel规划求解加载项以及SUMPRODUCT函数对目标函数进行矩阵乘积求解。自动求解后，Excel表格中的决策变量矩阵中显示供销平衡情况下的最佳分配方式为商品的供应产地有三个地区A1、A2、A3，销售地区有四个地区B1、B2、B3、B4：商品供应产地A1分配到需求地B1、B2地分别为2件、26件；商品供应产地A2分配到需求地B1、B4地分别为42件、12件；商品供应产地A3分配到需求地B3、B4地分别为24件、14件；。在该分配方式下，运输总成本最低为18，760元。规划求解的最优解结果见表3。

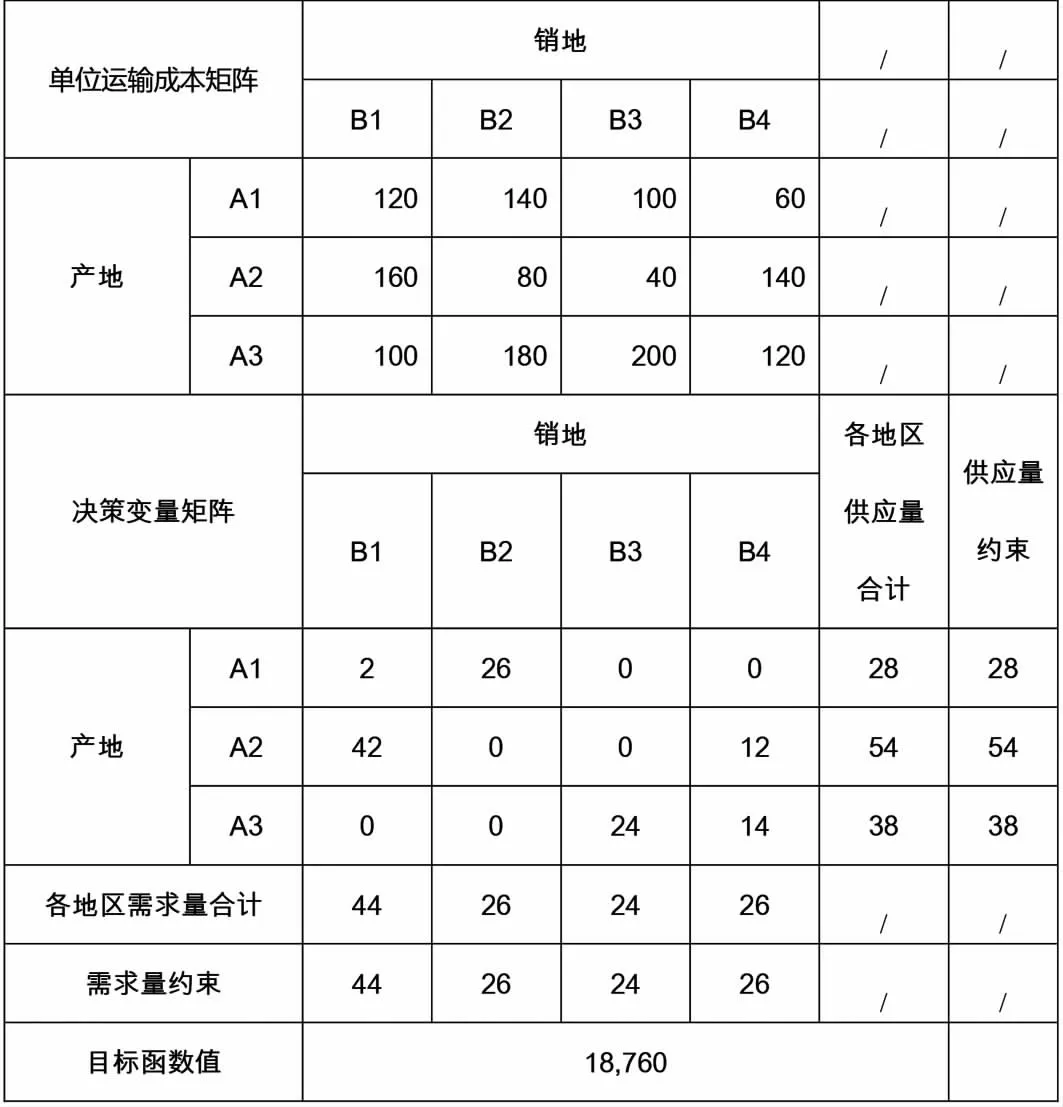
表3 整数规划求解最优解结果

4.总结：

本文利用整数规划原理，管理人员通过运用Excel将数学模型具象化，然后利用SUMPRODUCT函数以及规划求解加载项对目标函数求解可以得到商品运输分配的最优方案。整数规划建模原理可提高管理人员对供销两地之间的商品运输的分派问题，使得运输总成本最低。本文只讨论了供销平衡的理想状态下物流运输成本优化，但是实际状态并非适中处于供销平衡状态，所以如何进一步优化解决非供销平衡状态下的物流运输分配方案值得进一步探讨。C