射频直交比对四极质量分析器性能影响分析
邱云涛,冯 焱,成永军,陈 联,冯天佑,宋 伊,魏宁斐,冉 欣,郭 文
(兰州空间技术物理研究所 真空技术与物理重点实验室,兰州 730000)
0 引言
由于四极质谱仪具有体积小、结构简单、有良好的分辨率和灵敏度、调整和操作简便、工作压力范围宽以及响应速度快等优点,在气体分析及分压力测量中得到了广泛的应用。四极质谱仪是由离子源、孔电极、四极杆分析器和离子收集极等组成。四极杆分析器是质谱仪的核心部件,由四根对称排列的双曲面四极杆组成,两个对称的极杆彼此连接,两对极杆之间加直流电压和高频电压,直流电压和高频电压幅值保持一定比值。
对四极杆上的射频参数进行适当调试,可以提高四极质谱仪的性能指标。本文利用四阶龙格库塔法在Matlab软件中对离子在四极质量分析器中的运动进行数值模拟仿真,并对四极质谱仪研制样机进行射频参数调试实验,以验证仿真结果[1-3]。
1 四极质量分析器原理和建模
1.1 四极质量分析器原理
四极质量分析器结构图如图1所示。在四根金属材料圆形极杆上施加直流电压叠加高频交流电压的射频电信号,四极杆内部形成四极电场区域。离子在四极场的X-Y方向只受到电场力的作用,这种四极场产生的力将离子向四极场中心轴处拉拢聚焦,离子在Z方向不受电场力。
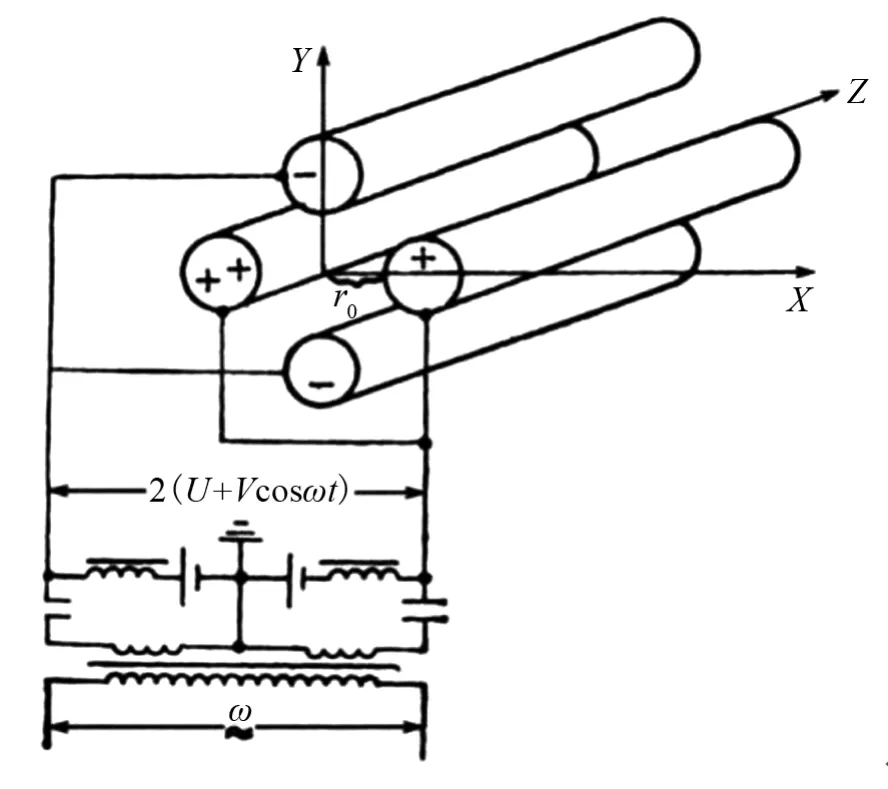
图1 四极质量分析器结构图Fig.1 Schematic diagram of quadrupole mass analyzer
在直流叠加射频电压的作用下,分析器内部产生电场如式(1)。

式中:φ为四极场中电位分布;U为直流电压;V为射频交流电压;ω为射频交流电压角频率ω=2πf,其中f为射频频率;r0为四极滤质场半径;x、y、z为四极场中的空间位置坐标;t为时间。
一般情况下,在离子源处被电离后的离子失去一个电子带一个正电荷,所以离子一般所携带的电荷量e的值为电荷常数1.6×10-19C。当质荷比为m/e的离子沿Z轴进入四极场时,在电场力的作用下离子的运动方程如式(2)[4]。

式中:e为电荷量;m为分子或原子的质量。该式表明,离子在Z方向作匀速运动,在X、Y方向为震荡周期运动,X、Y方向的周期运动规律为二阶微分方程,类似于Mathieu方程。采用参数变换如式(3)。
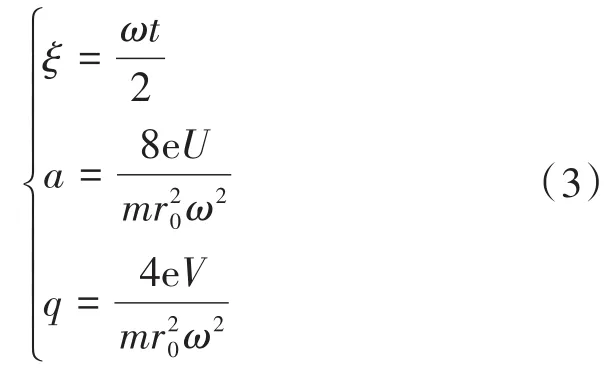
经过参数变换后离子运动方程可以写成标准的Mathieu方程如式(4)[5]。

四极场区域中离子的运动方程具有稳定解和不稳定解,X和Y方向的运动都是稳定解的区域叫做离子运动的稳定区,只有处于稳定区中的离子作稳定震荡运动时,离子才可能穿过四极场区域被分析。第一稳定区如图2所示,纵坐标为a,横坐标为q。(q,a)值落在第一稳定区中的离子运动轨迹为稳定震荡。由式(2)和式(3)可知,(q,a)值和四极滤质场半径r0,离子本身属性m、e,射频电学参数直流电压U,交流电压V,射频频率f紧密相关。在机械误差已经满足的情况下,射频电源电参数的调制极大地影响(q,a)值,从而影响四极质量分析器的性能。

图2 第一稳定区放大图Fig.2 Enlarged view of the first stable area
1.2 建立四阶龙格库塔求解离子运动的数学模型
Mathieu方程是标准的二阶微分方程,常用数值解法。四阶龙格库塔法能够很好地求解一阶线性微分方程,对于高阶方程也可以通过降阶为一阶微分方程后求解。对于一阶微分方程,使用四阶龙格库塔法的数值解公式如下[6]:

式中:h为计算步长;k1、k2、k3、k4为需要设定的参数;y为需要求解的参量。对于满足式(4)的离子运动Mathieu方程为二阶微分方程,在利用四阶龙格库塔法求解时,需要进行如式(6)的降阶变化。离子运动Mathieu方程降阶后就是式(6)中一阶微分方程,离子在X方向运动方程的四阶龙格库塔法数值解法如式(6)(7)(8)(9)[7-8]。
式中:x为离子在X方向运动的位移量,也是四阶龙格库塔法需要求解的量;g表示对x求导后的参数;F(tn,xn,gn)是式(6)中的表达式;kn和Ln是需要反复迭代得出的参数。离子在Y方向运动方程的四阶龙格库塔法数值解和X方向的求解方式相同,只需要依据式(4)改变部分参数和符号即可。
根据进入四极质量分析器入口处的离子束状态设置仿真的入口条件,离子束由离子源电离产生,再由离子透镜引出。从四极质量分析器入射的离子束具有初始位置分布和初始速度角度分布,初始位置分布的面积以四极质量分析器入口端小孔的面积为准,并且由于离子源处离子透镜的聚焦功能,离子源中被电离的绝大部分的离子入射四极质量分析器的初始位置靠近Z轴,并且离子入射的角度沿Z轴接近0°。则仿真的入口条件是离子的初始入射角度分布和初始入射位置分布均按正态分布进行计算。离子运动的初速度大小v0基于离子在离子源处获得的能量计算,如式(10)。

式中:U0为离子源给离子的有效加速电压;v0为离子被加速后进入四极质量分析器入口处的速度。
设置仿真的出口条件,针对以下两种情况分别判断离子是否飞出四极质量分析器。
(1)在四极质量分析器区域最大位移小于场半径,即umax (2)出口位移量小于出口孔径,即uout 以上两个判断条件必须同时满足,离子才能成功穿过四极质量分析器并被分析。 仿真中涉及的重要参数包括入口条件、出口条件、四极场属性和离子本身属性决定的(q,a)值。根据仿真的入口条件表述,初始的入射离子入口处截面离子数量和离子入射角度的分布都按照正态分布处理,离子束的数量选择为500个,以这些条件为基础进行离子束在给定四极分析场参数下轨迹仿真。在四极质量分析器中离子完整的运动过程是经历了多次在X-Y平面的四阶龙格库塔法运算,经过多次循环运算后的运算结果保存在数组中,运算结果包括通过四极质量分析器的离子和未通过的离子。离子束仿真主要研究出口位置通过的离子数量,而出口离子数量和初始离子数量的比值表示离子束经过四极质量分析器的通过率,通过率则代表四极质量分析器的滤质能力。 开展不同组斜率为a/q的质量扫描线的质量分辨能力仿真分析,通过固定q=0.706,改变不同的参数a,以获得几组不同斜率的a/q。a/q是第一稳定区中a与q的比值,也代表质量扫描线的斜率,而a/2q代表实际四极质谱仪中的射频电参数U/VPP,即射频直流电压与交流电压峰值之比。以图2中质量扫描线和第一稳定区为依据,对于不同组斜率为a/q的质量扫描线,同步改变(q,a)值,使(q,a)值可以沿着该斜率的质量扫描线移动,质量扫描线和第一稳定区所在的稳定三角形相交,(q,a)值落在相交线段中的离子可以通过四极质量分析器,该相交线段的长度经过式(11)参数转换后就表示可测得的质量范围与分辨本领。 式中:R为质量分辨率;∆m为单峰的半峰高处的峰宽。仿真结果如图3,随着a/2q增大,质谱峰峰宽越窄,但最大峰的通过率会降低。这意味着a/2q越大,四极质量分析器的质量分辨能力越高,离子通过率越低,离子信号强度也就越低,这也反映了质量分辨能力越高、灵敏度越差的仪器性能问题。实际调测四极质量分析器性能,需要找到一个合适的a/2q,既有较高的质量分辨能力,又要有较多离子数量通过。四极质谱仪的分辨能力以单峰的半峰高处的峰宽(Full Width Half Maximum,FWHM)表示,本文仿真与实验都是针对氮气分子展开,真空室中其他残余气体离子含量很少导致其他残余气体离子的灵敏度低,因此其他残余气体成分对实验结果的影响很小。主要通过离子峰宽形状与离子信号强度来分析射频直交比对四极质量分析器的性能影响。 图3 不同a/2q下离子通过率曲线Fig.3 Ions pass rate curves at different a/2q 四极质谱仪的离子源包括EI源、电离室、引出电极和离子聚焦透镜。为了对仿真结果进行实验验证分析,将四极杆质谱仪样机的各个部件接入质谱室测试系统,进行质谱峰实验测试[9]。建立四极质谱仪样机测试系统,主要由四部分组成:抽气系统、配气系统、测量系统以及烘烤系统。 选择不同射频直交比电学参数进行实验。实验前对真空室进行加热烘烤并抽气将压力降至1×10-4Pa以下。质谱分析室引入氮气,进样压力约为3×10-4Pa。基于第一稳定区的顶点的要求,直流电压测量值U和交流峰峰值VPP在经过式(12)的参数变化后就是理论直交比数值。 实验过程中其他参数不变,通过调节射频电源直流电压与交流电压峰值的比值,获得进样气体特征峰离子流变化情况,确定特征峰对应的射频电源交流电压幅值及其直交比最佳比值。开展直交比为0.04、0.08、0.085、0.09和0.16等情况下的收集极离子流随射频电源交流电压峰值变化规律实验,结果如图4所示。 图4 不同射频电源直流电压与交流电压峰峰值下的离子信号变化实验曲线Fig.4 Variation curves of experimental ion signal under different RF DC voltage U and AC voltage VPP 由图4可知,对比不同直交比情况下离子流信号随射频电源交流电压峰值变化规律,直交比由0.04逐渐增大到0.09,离子信号值最大值无明显衰减,都具有明显宽峰。虽然离子信号的峰宽随直交比增大而变窄,但降低幅度不明显,无法做到很好的离子分辨。而在直交比为0.16时,射频电源交流电压峰值为258.30 V时,出现一个明显谱峰,和其他直交比的质谱峰相比峰宽明显变窄,但同时信号峰值降低。根据式(13)计算获得第一稳定区顶点位置处对应的射频交流电压峰峰值为255.64 V,两者差别不大。 式中:m为氮气的质量,4.65×10-26kg;ω为射频电源交流电压角频率ω=2πf,其中f=1.939 4 MHz;r0为四极质量分析器场半径,取4.091 mm。 实验结果表明射频电压直交比越大,越靠近第一稳定区的顶点,质谱峰越窄,分辨能力越好,但离子通过率降低,相应的离子信号强度降低。 为了进一步验证实验与仿真的一致性,进行a/2q=0.04、0.08、0.085、0.09、0.16的离子通过率仿真,结果如图5所示。仿真结果与实验结果在趋势上具有一致性,并且仿真结果中氮气分子主峰28 amu所对应的交流电压峰值VPP=255.64 V,与实验结果258.30 V接近。仿真结果在主峰附近的离子峰形与实验结果基本一致,但是峰值在220 V以下时不同,这是由于实验中真实氮气分子具有14 amu的副峰,所以实验中在129 V交流电压峰值附近仍有信号。仿真中只关注氮气离子的主峰28 amu,所以在一定峰值以下信号开始全部衰减。在主峰28 amu附近仿真结果和实验结果一致,所以仿真结果符合射频直交比增大,分辨能力越好,离子通过率越低的规律。 图5 不同射频电源直流电压与交流电压峰峰值下的离子通过率变化仿真曲线Fig.5 Variation curves of simulated ions pass rate under different RF DC voltage U and AC voltage VPP 本文对离子在四极质量分析器中的运动进行了仿真,并且对研制的四极质谱仪样机进行射频电参数调试实验。研究了离子在四极质量分析器中的运动特性,以及四极质量分析器分辨能力的影响因素。得出如下结论: (1)仿真结果表明,通过调整射频控制模块来选择不同的直交比检测离子时,四极质量分析器会得到不同的质量分辨能力,并且离子束通过率也会不同,进而导致离子峰信号强度不同。质量分辨能力越高,离子信号强度越低。 (2)在实际调试四极质谱仪样机的实验过程中,选定不同射频直交比参数得到对应的氮气质谱峰图,改变直交比从而调节提升四极质谱仪的分辨能力,同样得到质量分辨能力越高,质谱峰信号强度越低这一规律。最后根据实验实际调试的直交比参数补充仿真计算,发现实验结果体现的规律与补充仿真计算结果相一致。2 四极质量分析器的仿真和实验验证
2.1 四极质量分析器的离子束仿真
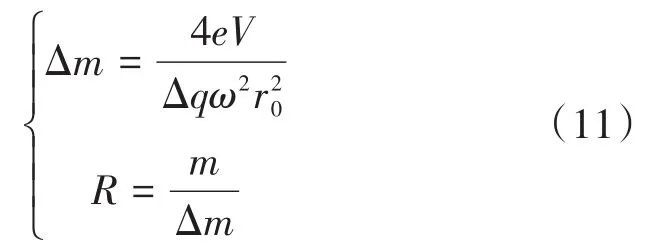

2.2 四极质谱仪样机性能测试实验




3 结论

