A novel genomic prediction method combining randomized Haseman-Elston regression with a modified algorithm for Proven and Young for large genomic data

Hailan Liu, Guo-Bo Chen

a Maize Research Institute, Sichuan Agricultural University, Chengdu 611130, Sichuan, China

b Phase I Clinical Research Institute, Zhejiang Provincial People’s Hospital, Affiliated People’s Hospital, Hangzhou Medical College, Hangzhou 310014, Zhejiang, China

c Key Laboratory of Endocrine Gland Diseases of Zhejiang Province, Hangzhou 310014, Zhejiang, China

Keywords:Genomic prediction GBLUP Randomized HE-regression Modified algorithm for Proven and Young

ABSTRACT Computational efficiency has become a key issue in genomic prediction (GP) owing to the massive historical datasets accumulated. We developed hereby a new super-fast GP approach (SHEAPY) combining randomized Haseman-Elston regression (RHE-reg) with a modified Algorithm for Proven and Young(APY) in an additive-effect model, using the former to estimate heritability and then the latter to invert a large genomic relationship matrix for best linear prediction. In simulation results with varied sizes of training population,GBLUP,HEAPY|A and SHEAPY showed similar predictive performance when the size of a core population was half that of a large training population and the heritability was a fixed value,and the computational speed of SHEAPY was faster than that of GBLUP and HEAPY|A. In simulation results with varied heritability, SHEAPY showed better predictive ability than GBLUP in all cases and than HEAPY|A in most cases when the size of a core population was 4/5 that of a small training population and the training population size was a fixed value.As a proof of concept,SHEAPY was applied to the analysis of two real datasets. In an Arabidopsis thaliana F2 population, the predictive performance of SHEAPY was similar to or better than that of GBLUP and HEAPY|A in most cases when the size of a core population(200) was 2/3 of that of a small training population (300). In a sorghum multiparental population,SHEAPY showed higher predictive accuracy than HEAPY|A for all of three traits, and than GBLUP for two traits. SHEAPY may become the GP method of choice for large-scale genomic data.

1. Introduction

Application of conventional marker-assisted selection (MAS) to animal and plant breeding has improved trial-and-error breeding based on phenotypic selection [1–4], but it is valid only for qualitative traits and quantitative traits controlled by large-effect quantitative-trait loci(QTL)and fails for polygenic traits controlled by many small-effect QTL [5,6]. With the development of highthroughput genotyping technology and statistical models, a technology called genomic prediction(GP)has been proposed and successfully applied to the improvement of quantitative traits[7–10].

In recent years, a variety of GP methods including parametric methods (such as GBLUP, BayesA, and LASSO) and nonparametric methods such as support vector machine (SVM), reproducing kernel Hilbert space(RKHS),and random forest(RF)have been developed [11]. GBLUP is a benchmark method whose computational process consists of two steps: (I) estimating heritability via restricted maximum likelihood (REML) and (II) computing genomic estimated breeding values(GEBV)by best linear unbiased prediction (BLUP). Both steps of GBLUP involve inverting a large genomic relationship matrix. To increase the predictive accuracy of GP, a very effective strategy is to increase training population sizes, but it is difficult or impracticable for conventional GBLUP to invert a genomic relationship matrix (GRM) for a large-sized training population [12]. For example, GBLUP failed to handle a massive set of greater than 3 million genotypes of U.S.Holstein cattle[13].The challenge is maintaining both predictive accuracy and computational efficiency in calculating with large datasets. Some efficient computational strategies have been developed in response to this challenge.(I)Misztal et al.[14]developed the Algorithm for Proven and Young(APY)to invert a GRM of millions of individuals.It greatly improves computational efficiency by obtaining the inverse of the GRM of a large training population using a small one randomly selected from it: the computational time of the inverse of GRM is only cubic in the size of the small population.Single-step GBLUP (ssGBLUP) based on APY has successfully performed GP of over seven million U.S. Holstein cattle [15,16]. (II)Liu and Chen [17,18] used Haseman-Elston (HE) regression based on genome-wise identity by state (IBS) to estimate heritability.The computational cost of HE is quadratic and that of REML is cubic in the training population size. Recently, Liu and Chen [12] developed a rapid genomic prediction method (HEAPY|A) combing the HE model with APY in an additive-effect model.

We present a super-fast GP method (SHEAPY) combining a modified APY with a scalable randomized algorithm for HE regression(RHE-reg),and evaluate its predictive accuracy and computing time.

2. Materials and methods

2.1. Genetic model

The basic model focuses only on additive effects, and is described as

in which y is an n×1 vector of the standardized phenotype of interest;μ is the overall mean of the model; 1 is an n×1 vector of ones;Z is an n×m matrix of standardized genotype coding values; u is the m×1 vector of the additive effects following; and e is an n×1 vector of residuals error following

2.2. Estimating heritability via randomized HE-reg

IBS-based RHE-reg is used to estimate heritability [19] as follows:

in which yiand yjdenote the phenotypes of individuals i and j(i，j=1···n, and i≠j), b0is the intercept, b1is the regression coefficient,Gijis the genetic relatednessbetween individuals i and j, and eijis residual error following. For a trait, its additive genetic variance is, and its. After some matrix algebra and numerical optimization, ordinary least squares is used to estimateand.The computational equation is described as

Here S represents the rounds of randomization implemented,and was set as 5 throughout the study. The sampling variance of the randomized estimator in Eq.(4)isaccording to matrix algebra.Under Eq.(3),it is straightforward to see thatin whichis a plug-in estimate from Eq.(4).By Taylor expansion,it can be proven that,and the bias vanishes when s is large enough. In particular,in which meis the effective number of markers for the population[18], and the bias is upon the realized value of. For breeding populations,meis often smaller than 100,so the randomized estimate is nearly unbiased.

2.3. Best linear prediction

Best linear prediction is used to compute genomic estimated breeding values (GEBV) for candidate populations:

2.4. A modified algorithm for Proven and Young

If there exists an additive relationship between entries, as is often the case in pedigree-based GRM in breeding programs, a numerical shortcut may be applied to reduce the computational cost of matrix inversion. An early realization of such a fast GRM inversion was discovered and implemented by Henderson [21].After decomposing a GRM into triangular and diagonal matrices,Henderson radically reduced the computational burden for the inversion of a pedigree-based GRM.Applying Henderson’s method to a single nucleotide polymorphism (SNP)-based GRM, Misztal et al. [14,22] proposed the Algorithm for Proven and Young (APY)to invert the GRM. The APY inverse is:

where Vccindicates the relationship matrix between the core individuals (a randomly selected subset of the training populations);PTnc=Pcn=V-cc1Vcn,in which Vcnrepresents the relationship matrix between the core and noncore individuals; and Mnnis a diagonal matrix of genomic Mendelian sampling for noncore individuals. Here Mnnis as follows:

in which Vnnindicates the relationship matrix between the noncore individuals.

Simplifying Mnn， we propose a modified APY that further reduces the computational cost of inverting the large matrix.When the core and noncore individuals are random samples,. Therefore Gcn［k，k］=0 and Mnn=diag（Vnn）=Inn,where Innis an identity matrix.When Mnn=Inn,the computational time can be further reduced without loss of accuracy of APY. The modified APY inverse is consequently

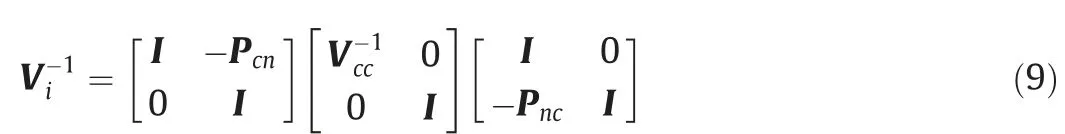
2.5. Simulated data

An F2population was simulated to compare the performance and computational time of GBLUP, HEAPY|A, and SHEAPY. A chromosome with a length of 5000 or 3000 centiMorgans [the recombination rate is c (c =0.01 for approximately 1 cM under the Haldane mapping function) between the ithand i+1（ ）thmarkers]was simulated. All markers on the chromosome were defined as QTL whose effects followed a standard normal distribution. Two conditions in the F2population were simulated:(1)multiple training population sizes (4000, 6000, 8000, and 10 000) with a fixed heritability (h2=0.75); (2) multiple levels of heritability(h2=0.1，0.3，0.5，0.7 and 0.9)with a fixed training population size(1000). Each simulation scenario was replicated 10 times.

2.6. Real data

Two datasets, for Arabidopsis thaliana and sorghum, were used to evaluate the predictive accuracy of GBLUP, HEAPY|A, and SHEAPY. (1) Phenotype and genotype data of an Arabidopsis thaliana F2population (P169) derived from a cross between Ts-1 and Tsu-1 were obtained from Salomé et al. [23]. This F2population consisted of 447 plants, and 240 SNP markers were genotyped. Seven traits, including DTF1 (days until visible flower buds in the center of the rosette),DTF2(days until inflorescence stem reached 1 cm in height),DTF3(days until first open flower),RLN(rosette leaf number), CLN (cauline leaf number), TLN (total leaf number: sum of RLN and CLN), and LIR1 (leaf initiation rate (RLN/DTF1)), were used. (2) The phenotype and genotype data of a sorghum multiparental population were obtained from Higgins et al. [24]. This population consisted of 5 biparental F2:3families including 724 lines and 9139 SNP genotyped markers. The adjusted phenotypic values of plant height in Urbana,Illinois,USA(HT-IL),plant height in Mexico(HT-MX),and flowering time in Urbana,Illinois,USA(FLIL) were used.

3. Results

3.1. Monte Carlo simulation

To assess the estimated heritability, predictability, and computational time of GBLUP, HEAPY|A, and SHEAPY, Monte Carlo simulations were performed for F2populations with four training population sizes(4000,6000,8000,and 10,000),candidate population size(100),heritability(h2=0.75),5001 equal-frequency biallelic markers, and recombination rate (c=0.01) (Table 1). For HEAPY|A and SHEAPY, 1/2 of the training populations were randomly selected as core populations. All methods showed nearly unbiased estimates of the true heritability of 0.75. All methods showed similar predictive accuracy. For example, when the size of a training population was 10,000,=0.704±0.010,=0.698±0.012, and=0.693±0.010. SHEAPY greatly reduced computational time in comparison with GBLUP and HEAPY|A. When the size of a training population was 10,000,TGBLUP=24972.2s, THEAPY｜A=2558.9s, and TSHEAPY=1005.8s.

The predictive accuracy of the three methods was also compared for multiple levels of heritability when the simulation parameters were set as training population size(1000),core population size (800), candidate population size (100), heritability(h2=0.1，0.3，0.5，0.7，and 0.9), 3001 equal-frequency biallelic markers,and recombination rate(c =0.01).SHEAPY showed better predictive ability than GBLUP in all cases and than HEAPY|A in most cases Table 2.

3.2. Genomic prediction of the traits in an Arabidopsis thaliana F2 population and a sorghum population

For the Arabidopsis thaliana F2population, the size of the training population was 300 for GBLUP,HEAPY|A and SHEAPY and that of the core population was 200 for HEAPY|A and SHEAPY(Table 3).For all seven traits,GBLUP and HEAPY|A showed similar predictive accuracy. For DTF1, RLN, CLN, and TLN the three methods performed similarly, and for DTF2 and DTF3, SHEAPY slightly outperformed the other two.Only for LIR1 did GBLUP and HEAPY|A show an advantage over SHEAPY(0.406±0.018 for GBLUP,0.402±0.019 for HEAPY|A, and 0.340 ± 0.022 for SHEAPY). Thus, the predictive ability of SHEAPY was similar to or better than that of GBLUP and HEAPY|A in most cases.

For the sorghum multiparental population,the size of the training population was 500 for GBLUP,HEAPY|A, and SHEAPY,and the size of the core population was 400 for HEAPY|A and SHEAPY(Table 4). GBLUP was superior to HEAPY|A for all three traits, and showed predictive accuracy similar to that of SHEAPY for HT-IL(0.842 ± 0.015 for GBLUP and 0.845 ± 0.011 for SHEAPY). GBLUP also outperformed SHEAPY for HT-MX and FL-IL. But the results were inconsistent with those from simulations, and investigating possible causes revealed that the relative frequencies of most of the reference alleles were between 0.6 and 1.0 at each marker locus and that this distribution held for 77% of the markers. There were no or only a few non-reference genotypes at some marker loci in the core population when the core population was randomly selected from the training population,and this deficiency severely impaired the predictive accuracy of HEAPY|A and SHEAPY.Accordingly, the predictive accuracies of GBLUP, HEAPY|A, and SHEAPY were evaluated again with 2081 markers whose non-reference allele proportions were greater than 0.415, to exclude the impact of invalid markers. SHEAPY then showed higher predictive accuracy than HEAPY|A for all three traits, and than GBLUP for HT-IL and FL-IL (Table 5).

Table 1 Comparison of the estimated heritability, predictive accuracy, and computational time of GBLUP, HEAPY|A, and SHEAPY for multiple sizes of training population based on 10 simulation in an F2 population.

Table 2 Comparison of the estimated heritability and predictive accuracy of GBLUP,HEAPY|A, and SHEAPY at multiple levels of heritability based on 10 simulations with a simulated F2 population.

Table 3 Comparison of predictive accuracy among GBLUP, HEAPY|A, and SHEAPY for seven traits in an Arabidopsis thaliana F2 (P169) population based on 10 simulations.

Table 4 Comparison of predictive accuracy among GBLUP, HEAPY|A, and SHEAPY for three traits in a sorghum F2:3 population based on 10 simulations with 9139 markers.

Table 5 Comparison of predictive accuracy among GBLUP, HEAPY|A and SHEAPY for three traits of a sorghum F2:3 population based on 10 simulations with 2081 markers.

4. Discussion

GP has increased the rate of genetic gain and reduced the generation interval. With its wide application, a massive quantity of historical datasets have been accumulated,with which large training populations can be established to achieve high predictive accuracy.But the dimension of GRMs will increase geometrically when multi-trait and/or multi-environment data are integrated into the GP model. Thus computational efficiency in predicting individuals with large-scale data emerges as a necessity.

Inversion of the GRM,an indispensable step in GBLUP,becomes very difficult when the size of the training population reaches150,000[25],and new methods such as APY,updating the inverse,and a recursive algorithm have been presented accordingly[22,26–27]. Chen [28] proposed HE regression based on IBS to estimate heritability,markedly reducing computational time in comparison with GBLUP by adoption of least-squares instead of REML estimation[17–18].Combining the merits of APY and HE,we have previously developed HEAPY|A [12], whose computational speed was over 13 times that of GBLUP when the size of a training population was 4000 and that of the core population was half that.

In this study, we developed a new computational approach(SHEAPY) combining RHE-reg with a modified APY in an additive-effect model. Removing the computation of a GRM between noncore individuals via replacement of Mnnwith Inngreatly accelerated the modified APY. When the size of a training population was 10,000 and that of the core population was half of it, the computational speed of SHEAPY was over 20 times of GBLUP and over 2 times of HEAPY|A with similar predictive accuracy. When the size of a training population was relatively small,as it was in this study,the size of the core population should be increased to obtain predictive accuracy similar to or better than GBLUP. For example, the size of the training population was set as 300 and the core population as 2/3 of that (200) in the Arabidopsis thaliana F2population. The prediction results from the sorghum multiparental population showed that rare markers severely impaired the predictive performance of the SHEAPY owing to their low representation in the core population and accordingly should be excluded.

How to choose the core population is crucial but remains an open question. Pocrnic et al. [25] found that the optimal size of a core population depended on effective population size (for example, the optimal number is about 14,000 for Holstein and Angus cattle,12,000 for Jersey cattle,and 6000 for pigs and broiler chickens). It remains to be investigated which individuals need to be selected in order to further reduce the computational cost and maintain predictive accuracy in practice.

5. Conclusions

Integrating I) a randomized algorithm for estimating variance components in RHE-reg and II)a modified APY,the proposed SHEAPY algorithm showed marked superiority to GBLUP and HEAPY|A in computational efficiency. A computational framework was developed under the additive-effect model. A computer program(SHEAPY) is available from the authors.

CRediT authorship contribution statement

Hailan Liu:Conceptualization, Investigation, Formal analysis,Methodology, Writing - original draft, Writing -review & editing,Project administration.Guo-Bo Chen:Conceptualization, Investigation, Methodology, Writing - original draft, Writing - review &editing, Project administration, Funding acquisition.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgments

This study was supported by the National Natural Science Foundation of China to Guo-Bo Chen (31771392) and Zhejiang Provincial People’s Hospital Research Startup to Guo-Bo Chen(ZRY2018A004). The authors are grateful to Prof. James C. Nelson for English editing.