功率约束下低相关旁瓣的通导一体化波形研究

张智博，常 青，赵 娜，徐 昊

(北京航空航天大学电子信息工程学院，北京 100191)

0 引言

随着第五代移动通信系统的加快部署，无线通信信号在室内和室外的覆盖进一步密集，具有覆盖范围大、信号频带宽的特点，通信信号可以作为卫星导航信号较弱无法有效定位的补充，实现定位和通信一体化成为了提升频谱利用效率的关键技术之一。文献[2]提出了通信导航一体化的需求，通过融合地面通信、卫星通信、无人机通信系统等，实现全方位的空天地通导一体化。文献[3]对通信导航一体化技术进行了深入的总结，分析了研究演进情况、常见定位方法、信号体制设计等关键问题，并对毫米波、多输入多输出系统、波束成形等技术进行了展望。

通信导航一体化技术主要有两种设计思路，一是利用现有的通信和导航信号实现定位，二是设计新的一体化信号波形。文献[4]使用了4G网络中专用的定位参考信号，但是由于重复频率较低，定位精度仅几十米；文献[5]研究了4G-LTE信号的定位问题，并评估了其定位精度；文献[6]讨论了5G网络中的上行合作非正交多址技术在定位中的应用；文献[7]研究了一种新体制信号，在功率域对不同用户的通信信号进行复合，并利用正交频分复用技术使不同定位用户的信号相互正交；文献[8]讨论了一种利用正交频分复用信号协同进行通信和目标定位探测的设计方案，并进行了实际环境中的测试；文献[9]利用专门设计的通信协议进行基于毫米波的通信，并利用信号的回波确定目标位置。结合以上的设计思路，本文主要研究设计了新的一体化波形进行协同通信和定位。

无线数字通信系统中，基于正交调制，发射通信符号往往用星座图上的复数符号表示，信号的解调可以通过同向支路和正交支路上的信号幅度判决确定，此外通信性能往往利用误码率进行评估。在利用通信信号进行定位时，信号的传播时延往往由相关函数的峰值位置确定，因此相关函数的旁瓣性能对定时精度有直接影响，可以利用自相关函数的积分旁瓣电平和改进品质因数(Modi-fied Merit Factor， MMF)对波形的定时性能进行衡量。因此，本文结合上述2个指标，提出了一个加权优化问题以设计新的一体化波形，结合了自相关函数的加权积分旁瓣电平(Weighted Integrated Si-delobe Level，WISL)和星座图上的范数误差，并考虑了在波形设计时的波形总功率约束和波形恒模约束。本文利用变量交替迭代优化的方法进行问题求解，并设计了针对两种约束的问题求解算法，最终利用数值仿真验证了算法的有效性。

1 一体化信号的基带数学模型

1.1 信号模型及波形自相关性质

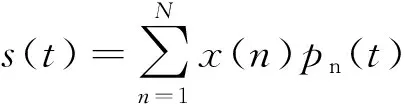
(1)

相关特性可以用来描述波形用于测距时的定时误差，波形的离散自相关函数可以表示为

(2)

其中，=0,…,-1。理想的自相关函数是仅在=0处取得峰值，而在≠0处其模值为0，因此波形设计的目标是使{()}≠0尽可能小。WISL可以描述这一性质

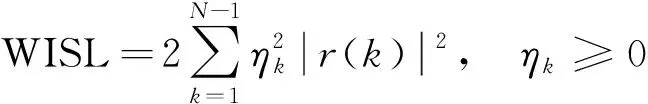
(3)

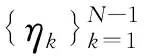
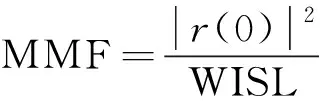
(4)

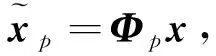
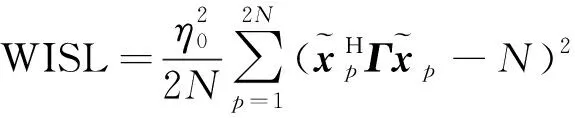
(5)

其中

(6)

由于在给定信号的功率时，越大的WISL会使MMF单调地降低，在本文中采用WISL指标衡量波形的相关性能。

1.2 通信及信道均衡

由于通信符号在时域上具有随机性的特点，且其信号表示形式与式(1)相同，可以考虑将其与测距信号进行一体化设计。实际通信系统中往往面临较强的多径效应，无线通信信道可以建模为线性系统，在本文中，考虑长度为的抽头滤波器模型。无线通信用户的接收信号可以表示为

(7)

显然，无线信道的多径效应引入了码间串扰，为了消除此影响，往往在接收端引入均衡器，即设计矩阵=[(:,1:)]，从而有

(8)

即在信噪比达到门限时可以满足正常通信的需求。

数字通信的基带符号可以用星座图上的复数点表示，注意到由于可以采用式(8)中的接收机均衡方案，接收到的符号和发射机发射的符号在不考虑噪声的情况下是相同的。因此，在设计发送序列时，只需要使实际发送的符号序列逼近期望发送序列，即可以用如下的范数误差(Norm Error, NE)指标衡量一体化符号的通信性能

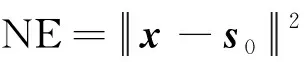
(9)

1.3 一体化波形的功率约束

在实际系统中，发射机的发射功率会受到功率放大器性能及系统供电等条件的约束，是具有性能上限的。因此，在一体化信号的波形设计时，也需要考虑信号的功率。常见的信号波形功率约束包括总功率约束和信号恒模约束。总功率约束可以建模如下，设信号的平均功率为，则有

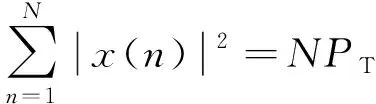
(10)

约束波形的模为恒定值以最大化功率放大器的效率，可以有如下的波形恒模约束

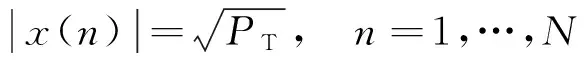
(11)

下面，将讨论这两种不同功率约束情况下的一体化信号的设计问题。

2 波形优化问题及求解算法

2.1 优化问题构建

由于式(5)中，WISL指标关于波形变量为四次函数，不易优化，定义=，引入辅助变量∈×1，其可以进行如下的等价转化

(12)

因此，在上述总功率约束和波形恒模约束的情况下，可以构造如下的一体化波形优化设计问题

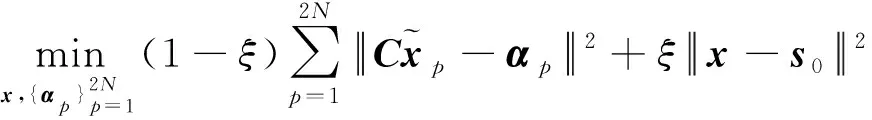
(13)

其中，0≤≤1为加权因子，用于调整对波形相关性能和通信性能的重视程度，即随着的增大，波形设计的优化问题将更着重于系统的通信性能。

2.2 总功率约束下的波形优化设计

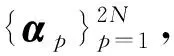
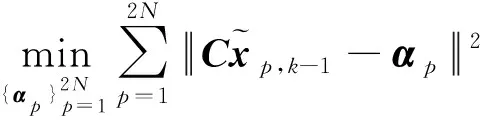
(14)

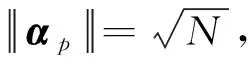
(15)

显然，取等号时，变量的取值为

(16)

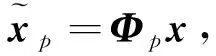
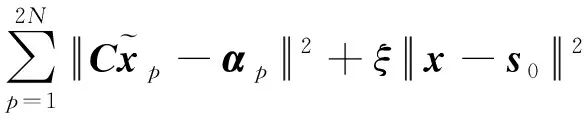
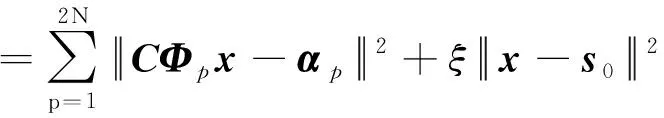
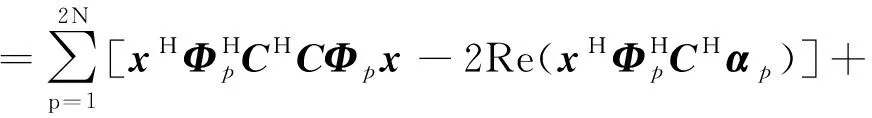
ξ-2Re()+常数

=-2Re()+常数

(17)

其中

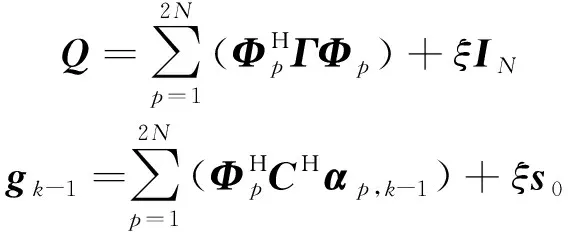
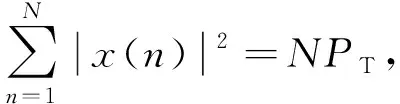
(18)

从而，=(+)-1，通过对进行特征值分解=，有

=

(19)

根据乘以酉矩阵不改变范数的性质，可以简化为

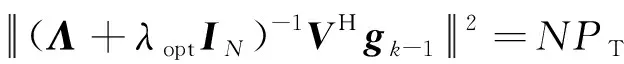
(20)

于是，可以构造出一个单调减的函数

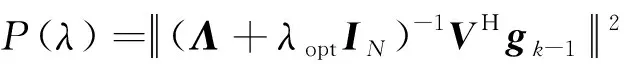
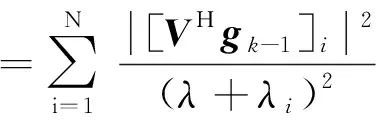
(21)

其中，是矩阵的第个特征值。由于()的单调性，可以利用一维线搜索的方法，确定出，并计算出变量的解=(+)。

2.3 恒模约束下的波形优化设计

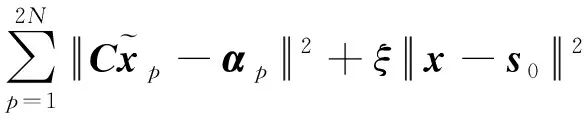
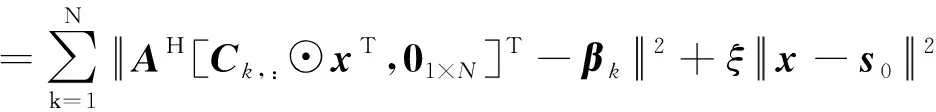
(22)

式中，⊙代表Hadamard积运算。显然，利用()=的约束，非常数部分可以写为

(23)

显然可以拆分成个优化问题分别针对()求解，且有

()=

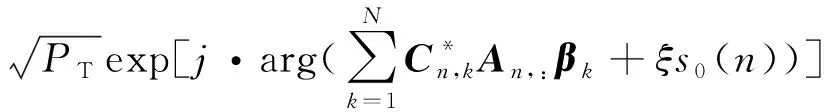
(24)

3 仿真验证

为了验证本文研究的算法在总功率约束和恒模功率约束下的有效性，进行了相应的仿真分析。选取设计的通信导航一体化序列的长度=101，信道抽头滤波器的长度=5，通信调制方式为QPSK调制，信号的功率值=1。设定了加权矩阵=10，～自1.3线性递减至1.1，并取其余权重为0，即期望的自相关函数在零时延附近的旁瓣被抑制。设置所有迭代的波形的初始值为期望通信符号序列。

首先，分析比较两种不同约束下算法的有效性，以及目标函数对加权因子的敏感性。设置相同的加权因子=00909，仿真的通信接收星座图及利用公式10log(()(0))计算出的归一化自相关函数如图1和图2所示。从图1中可以看出，设计的一体化波形的波形星座点均在期望星座点附近，且对于总功率约束条件，呈现围绕期望星座点的样式；对于恒模约束条件，其在恒功率圆上靠近期望星座点分布。图2中对比了归一化自相关函数，可以看出对于两种约束条件，在设定权重值(第1～20点)的范围内，自相关函数的旁瓣均有所抑制，但由于对加权因子的敏感性不同，其抑制程度有所不同。图2中3条曲线的MMF值分别为：初始波形2.6394,总功率约束1264.9122,恒模约束4.1103；相应地在信噪比为12dB的情况下的误码率为：初始波形7.168×10,总功率约束1.333×10,恒模约束8.229×10。可以看出，具有MMF越大，误码率越高的特点，能够充分看出优化问题在自相关函数性能和通信误码率性能之间的权衡。

图1 通信星座图(ξ=0.0909)Fig.1 Constellation plot of communication(ξ=0.0909)

图2 归一化自相关函数(ξ=0.0909)Fig.2 Normalized autocorrelation function(ξ=0.0909)

为了给出较为公平的性能比较，以下通过合理选择加权因子的值，使得两种不同约束下波形的MMF值均为12，所设定的加权因子的值分别为：总功率约束0.8795，恒模约束0.0196。在此情况下，给出了如图3～图5所示的归一化自相关函数图、通信星座图、通信误码率曲线图。从图3中可以看出，在MMF值相同时，在两种不同约束下，对自相关函数旁瓣抑制的程度相当。图4反映了通信的星座点，把图4和图1作对比可以看出，随着加权因子的增加，通信星座点呈现出聚集于期望星座点的特点，即一体化优化目标函数更加强调对通信性能的优化，反之亦然。图5给出了在相同MMF情况下的误码率曲线，可以看出，针对自相关函数性能的优化，使得通信误码率相较于期望波形有所下降，同时总功率约束下的误码率低于恒模约束下的误码率。这是由于总功率约束的优化求解空间更大，从而能够达到更好的通信性能，但对功率放大器的设计提出了更高的要求。

图3 归一化自相关函数(MMF=12)Fig.3 Normalized autocorrelation function(MMF=12)

图4 通信星座图(MMF=12)Fig.4 Constellation plot of communication(MMF=12)

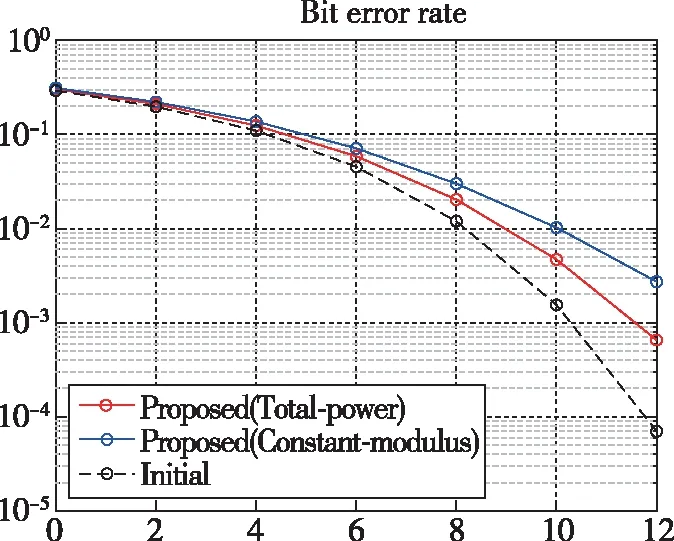
图5 误码率图(MMF=12)Fig.5 Bit error rate(MMF=12)

4 结论

本文针对通导一体化波形设计问题，提出了一种在实现通信功能的同时降低波形的自相关函数旁瓣的加权优化问题，并给出了波形设计算法。本文的工作和主要结论如下：

1)分析了通信性能和定时性能的衡量指标，以星座图上的范数误差衡量通信性能，以自相关函数的WISL衡量波形的定时性能，并构建了加权优化的一体化目标函数。

2)基于变量交替迭代优化的算法，在分别考虑总功率约束和波形恒模约束的情况下，给出了相应的波形设计优化算法。

3)数值分析表明，通过加权优化可以实现两性能的权衡，既能够实现对通信信号自相关函数旁瓣的抑制，也能够逼近期望的通信符号。

4)在两种不同功率约束下，一体化优化目标函数对加权因子的敏感度不同，且在实现相同的自相关函数品质因数时，在总功率约束下能够实现更好的通信性能。