调和分析方法在股票市场周期波动研究中的应用

王玮彬

（三明学院 经济与管理学院，福建 三明 365004）

西方国家对经济周期的研究已经持续了近160年，期间不乏具有里程碑意义的经典理论成果。1862年，Juglar首先提出了平均长度8～11年的市场经济周期理论（Juglar周期）[1]25-42；20世纪初，Kitchin和Kuznets先后分别发现了平均长度约3.5年的库存周转周期（Kitchin周期）[2]10-16，以及平均长度约20年的建筑周期（不动产周期或Kuznets周期）[3]453-457。上述三种理论历经多年的论证与完善，在宏观经济实践中已得到大量实证，持续衍生出诸多应用创新。马家喜[4]89-91分析论证了中国市场经济波动中存在典型的Juglar周期现象；Grinin[5]138-187基于Juglar周期建立因子模型实证分析了当时的全球经济危机；徐志向和张敏[6]64-75分析了改革开放前后中国经济周期的转变，发现经济周期的演变机制主要体现为政治周期、经济机制内部调节周期以及创新周期“三位一体”的时空转换；隋新玉和王云清[7]129-133基于股市周期和宏观经济周期波动趋势的实证分析,发现我国股市周期和宏观经济周期之间存在部分同步部分背离的关系。聂丽等[8]132-141分析总结了新兴市场经济周期的特征事实与产生机制，认为新兴市场经济周期对世界经济周期将产生更加显著的影响。

时间序列调和分析是现代分析数学领域的核心技术，其中傅里叶分析（Fourier analysis）可以通过时域-频域变换，对具有简谐波动特征的时间序列数据进行频谱共振分析[9],已被有效应用于经济领域的周期性规律分析。闫中晓和贾永飞[10]13-16通过谱分析技术验证了科技投入和产出增长速度与中国经济增长速度之间的领先滞后关系；邬琼[11]3-6利用谱分析方法对我国经济增速数据进行研究，认为我国当前正进入新一轮库存周期；李庆晗[12]72-75基于谱分析方法对中国宏观经济波动与股票市场的周期联动效应进行研究，发现宏观经济周期对股票市场指数变化具有长期范围内的滞后影响。

本文即通过经济周期理论与时间序列信号分析技术的结合，应用调和分析方法去构建经济周期多因子模型，对全球股票市场的价格时间序列数据进行因子函数回归拟合，实证检验了宏观经济周期对股票市场的影响。

一、股票市场周期波动规律的调和分析实证

以上证指数每月最后一个交易日的收盘价序列为例，考察A股市场的周期性波动规律。

（一）对数同比序列计算

上证指数1990年12月至2021年8月的月度收盘价时间序列见图1，通过以下公式对其进行平稳化处理，得到原始数据的对数同比序列：

图1 上证指数月度收盘价时间序列

其中，Xn是上证指数月度收盘价时间序列，Xn-12是上一年度同月收盘价序列。Yn是取对数同比后的新序列，具有围绕中心值周期性波动的趋势，见图2。

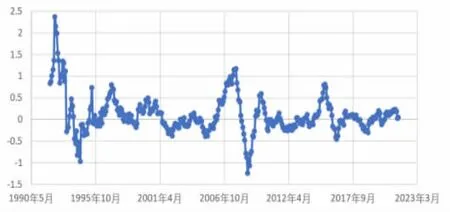
图2 上证指数月度收盘价对数同比序列

（二）快速傅里叶变换频谱分析

通过以下公式，对上证指数对数同比序列进行快速傅里叶变换 （Fast Fourier Transform，FFT），得到频谱：

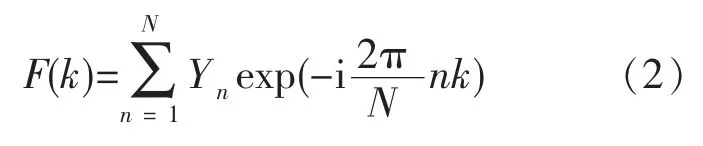
其中，Yn是上证指数对数同比序列，k表示频谱图中的任意频率，N是时间序列Yn中的数据点个数表示把函数f(n)按照 n=1～N进行累加求和。F(k)是Yn进行FFT变换后的频谱，见图3，其中横轴表示的是“频率/年-1”，纵轴表示振幅。

图3 上证指数同比序列频谱图

对照前述经济周期理论中的Kitchin周期（约 3.5 年）、Juglar周期（约 8～11 年）、Kuznets周期（约15～20年）的长度范围，分别在频谱的f=0.285Hz（T=3.5 年）、f=0.115Hz(T=8.7 年)、f=0.061Hz（T=16.3年）处发现共振峰，即上证指数同比序列的波动包含以上三种频率的周期成分。经典周期理论对周期长度的预测并不是精确值，相当于一个给定范围内的模糊信号，因此我们用具有高斯分布的带宽滤波代替单一频率的线谱滤波，对FFT频谱进行信号共振分析。

根据以上频谱分析结果，近似取Kitchin周期长度T=40个月、Juglar周期长度T=100个月、Kuznets周期长度T=200个月，并按以下高斯滤波公式（取滤波带宽为1）代入三种经典周期的不同长度T，对上证指数频谱图分别进行高斯滤波，过滤随机高频噪声：

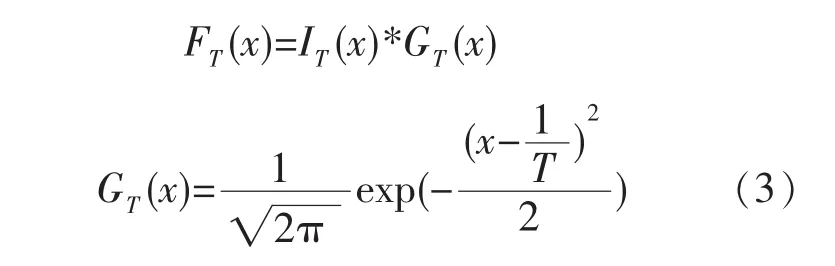
其中，x是频率因变量，GT(x)是中心频率取时的高斯核，IT(x)和 FT(x)分别为输入频谱图和高斯滤波后的输出频谱图，符号“*”表示卷积操作。

三种经济周期的高斯滤波结果见图4～6，其中横轴表示的是“频率/年-1”，纵轴表示振幅。可见均能够在频率与各自周期长度相匹配的频谱位置，观察到单一共振峰，即证实了Kitchin周期、Juglar周期、Kuznets周期引起的简谐振荡在上证指数价格时间序列中同时存在，是上证指数价格波动规律的重要组成部分。

图4 Kitchin周期的高斯滤波结果（T=40个月）

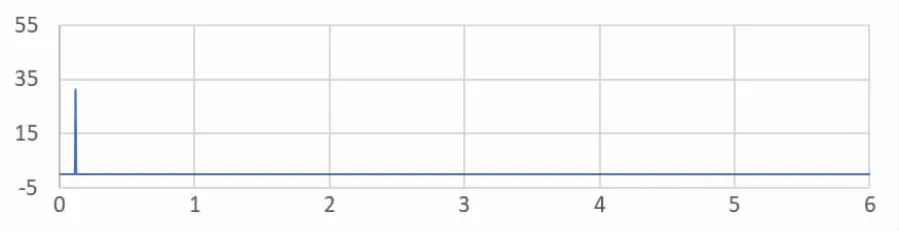
图5 Juglar周期的高斯滤波结果（T=100个月）

图6 Kuznets周期的高斯滤波结果（T=200个月）

（三）全球资本市场实证分析

通过选取中国沪深300指数、美国标普500指数、德国DAX指数、法国CAC40指数等作为调和分析对象，在全球资本市场对上述结论进行验证。同样把以上四个指数每月最后一个交易日的收盘价作为输入时间序列，按照公式（1）转化成对数同比序列，通过公式（2）进行快速傅里叶变换得到各自的频谱；根据公式（3）分别选取 Kitchin周期长度T=40个月、Juglar周期长度T=100个月、Kuznets周期长度T=200个月，对中国沪深300指数、美国标普500指数、德国DAX指数、法国CAC40指数等四个指数的频谱进行高斯滤波，并得到各自滤波后的频谱。相关频谱及三周期的高斯滤波结果见图7～10，各图中从上往下依次为FFT频谱图和T=40个月、100个月、200个月的高斯滤波结果。

可以观察到，四大指数频谱均在周期长度为40个月、100个月、200个月对应的频率处出现了幅度较大的共振峰，与上证指数的频谱分析结果一致。

图7 沪深300频谱及三周期高斯滤波结果

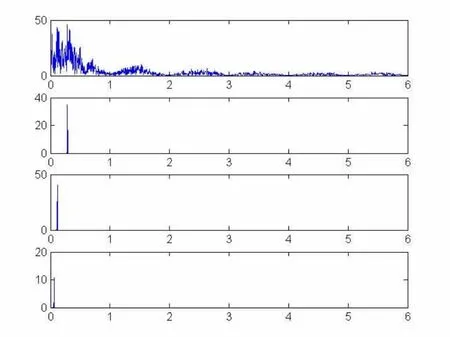
图8 标普500频谱及三周期高斯滤波结果

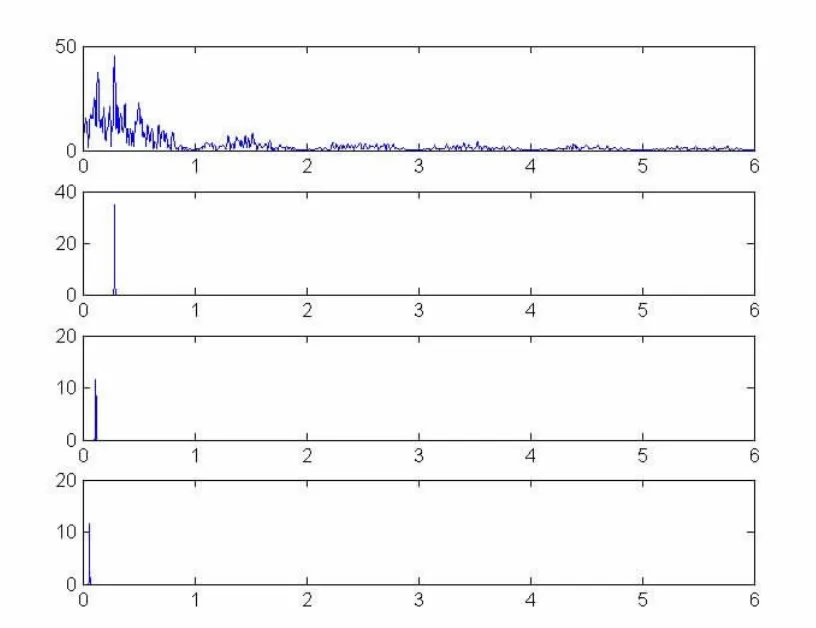
图9 德国DAX频谱及三周期高斯滤波结果

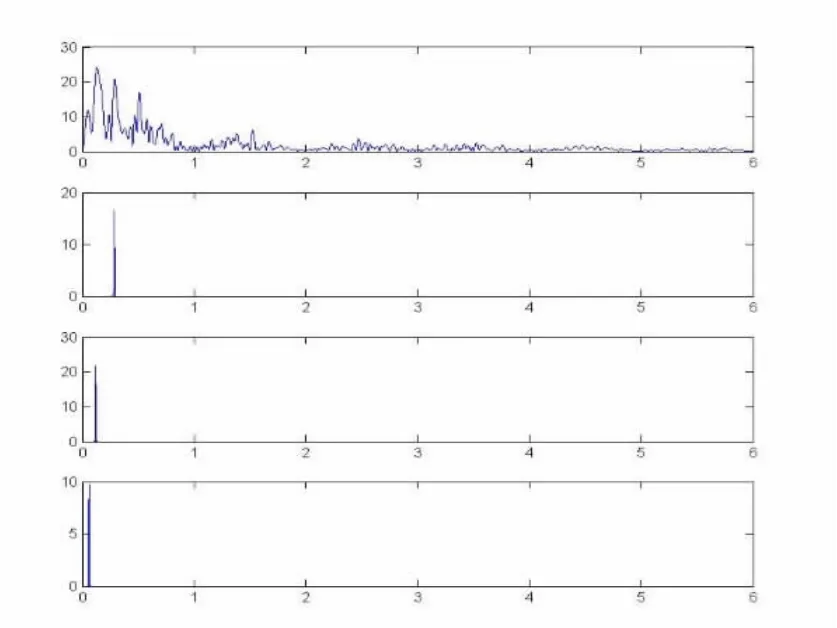
图10 法国CAC40频谱及三周期高斯滤波结果

相似结论也可在债券市场及大宗商品市场观测到，即全球主要国家资本市场的价格波动在相同频率处发生了共振，Kitchin周期、Juglar周期和Kuznets周期引起的简谐振荡是全球资本市场波动共有的特征分量。因此，经典经济周期理论可以解释资本市场价格波动的部分原因，三种周期共同构成了资本市场周期性波动的普适规律。

二、资本市场经济周期多因子模型的构建——以纳斯达克指数为例

（一）经济周期多因子模型的回归拟合分析

以美国标普500指数的价格对数同比序列为例，按照以下回归方程建立经济周期多因子模型，并对所有系数进行多元回归拟合：

其中，Y 为拟合因变量，X1，X2，X3分别是周期长度为40个月、100个月、200个月的三种周期因子，即图4～6对应的高斯滤波结果经过FFT逆变换后得到的周期因子序列。公式（4）中a、b、c、d为回归系数，其中a为常数趋势项，ε为残差项，b、c、d 为复数周期因子系数，bX1、cX2、dX3分别为三种周期的简谐振动项，即拟合因变量Y在三个周期因子上的分量。

标普500指数经高斯滤波后的周期多因子模型回归拟合结果见图11，与对数同比序列的低频波动趋势基本一致。公式（4）中的趋势项a和三个周期因子变量的回归系数b、c、d分别为：a=0.002， b=1.489，c=1.771，d=2.261。 该回归分析拟合优度的判定系数R2=0.602，p值为1.17×10-55，即拟合变量为显著有效变量，经济周期多因子模型的回归拟合结果可以解释标普500指数的部分波动规律，同时该指数的波动信号仍存在一定的随机高频噪声 （因为高频噪声在回归拟合前已被高斯滤波算法过滤）。

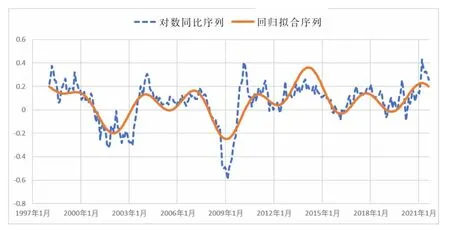
图11 标普500指数的周期多因子模型回归拟合结果

选取全球股票市场具有区域代表性的股票指数时间序列数据，应用公式（4）的经济周期三因子模型分别进行高斯滤波后的回归分析，得到结果见表1。可以发现，除我国的上证指数和恒生指数回归拟合优度在0.4～0.5之间外，其他数据的拟合扰度基本均在0.5以上。另外，所有数据回归方程的残差项均通过了平稳性检验。

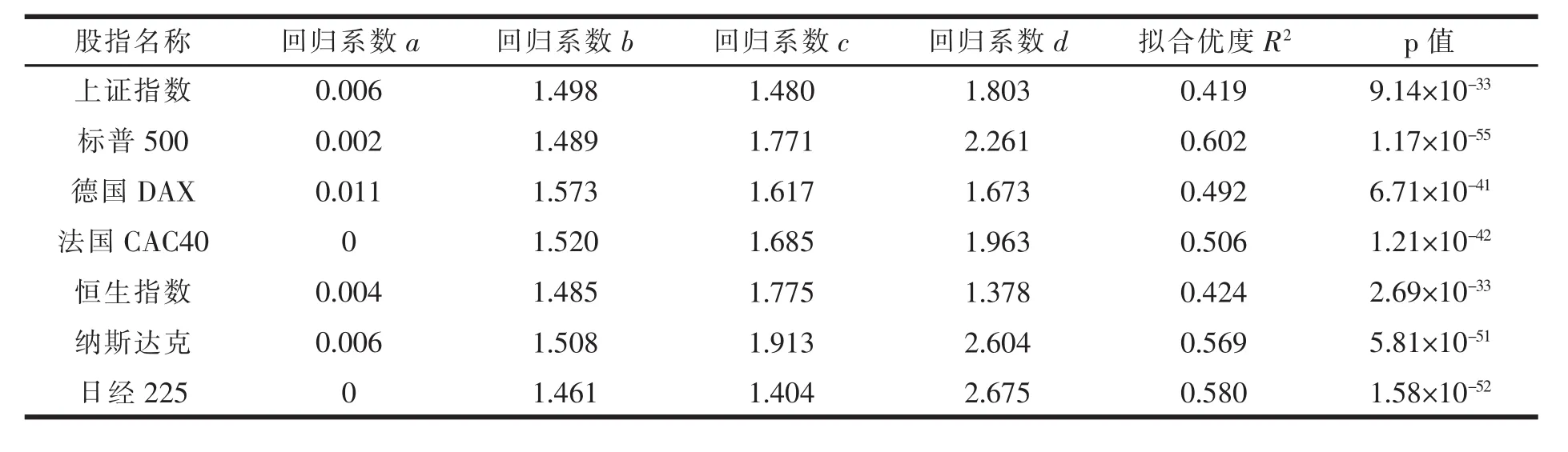
表1 经济周期多因子模型回归系数与拟合扰度数值表

因此，可以认为三种经济周期的复合作用对股票市场形成了显著影响，且公式（4）中的多因子模型可以解释股票市场的部分波动规律。

（二）经济周期多因子模型的回归预测分析

按照公式（4）确定所有回归系数，对标普500指数建立了周期多因子模型后，即可通过以下公式，进行标普500指数对数同比序列的未来波动趋势的预测分析：

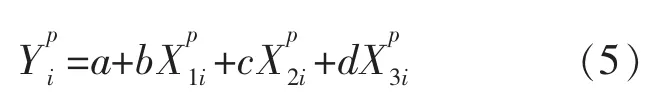
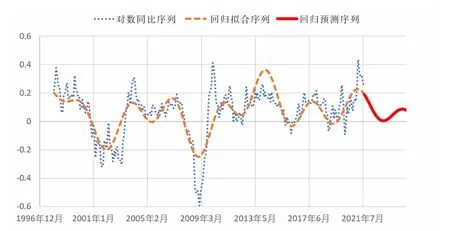
图12 标普500指数的周期多因子模型回归预测结果

（三）预测结果与实际数据的比较

选取纳斯达克指数1997年1月至2011年12月的月收盘价格时间序列，运用周期多因子模型对公式（4）进行回归拟合，基于拟合结果对2012年1月至2021年8月的样本外数据进行预测，并与同时间区间内的真实数据进行比较，见图13。与2012年1月至2021年8月的纳斯达克指数实际数据相比，周期多因子模型的预测结果显示出基本一致的总体波动趋势，即该方法能够用于预判股票市场的部分周期性波动规律。

图13 基于周期多因子模型的纳斯达克指数预测结果与真实数据比较

三、周期多因子模型应用——股票市场经济周期规律的历史演化

构建股票市场周期多因子模型，不仅能对其周期性波动规律进行预测，还可用于演示与分析资本市场经济周期规律的历史演化过程。在公式（5）中，经过FFT逆变换得到的周期因子都是复数值，每一个因子值均包含对应经济周期在当前时间点的相位信息和幅度信息，假设复数因子值X=p+qi,则周期因子相位信息和幅度信息的计算方法如下：

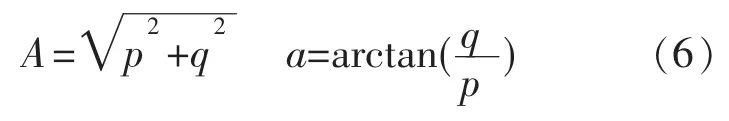
其中，A为周期因子的幅度值，α为周期因子的相位值，分别由周期因子值X的复数模与复数相位角表示。

以历史最悠久的资本市场价格指数——美国道琼斯工业指数为例，输入其1900年1月至2021年5月间的历史数据，设定观察窗口为20年的滚动样本区间，连续构建周期因子模型进行滚动预测，得到三种经济周期在1920年4月至2021年8月的预测因子序列每一组周期因子值均由过去3至243个月的历史数据，按照公式（4）和公式（5）建立因子回归模型并进行外推预测获得。

周期因子的相位信息可用于表示对应经济周期规律的当前运行状态，其取值在[-π，π]之间周期性变化。按照公式（6），对上述周期因子值序列进行相位信息计算，可以获得美国道琼斯工业指数在1920年4月至2021年8月间，对应三种经济周期的相位信息序列,其历史演化过程见图14～16。

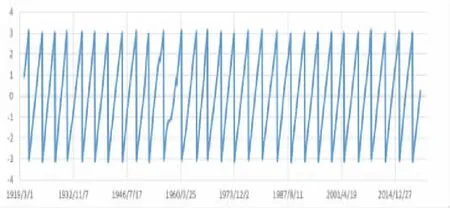
图14 Kitchin周期相位的历史演化过程

图15 Juglar周期相位的历史演化过程

图16 Kuznets周期相位的历史演化过程

（一）经济周期相位的历史演化

可以看出，相位信息序列的连续性可以直观反映对应经济周期规律的运行稳定性以及对应周期因子的时间有效性。在三种经济周期规律中，Kitchin周期在过去近100年间运行得最为连续平稳，几乎没有发生相位畸变，证明了商品供求关系引起的库存周转周期是资本市场稳定存在的客观规律，其有效性几乎不受世界大战、技术革命、政策变动、经济危机等因素的影响。Juglar周期与Kuznets周期在20世纪七八十年代出现了显著的相位畸变，可能与美国经济危机、信息技术革命、经济全球化等因素有关，其中Kuznets周期较Juglar周期信号失真更严重，因子有效性更弱，影响因素也更多。

（二）经济周期幅度的历史演化

类似于周期因子的相位信息，其幅度信息也可以反映经济周期规律对资本市场的影响能力。同样按照公式（6），对上述周期因子值序列进行幅度信息计算，可以获得美国道琼斯工业指数在1920年4月至2021年8月间，对应三种经济周期的幅度信息序列,其历史演化过程见图17～19。

图17 Kitchin周期幅度的历史演化过程

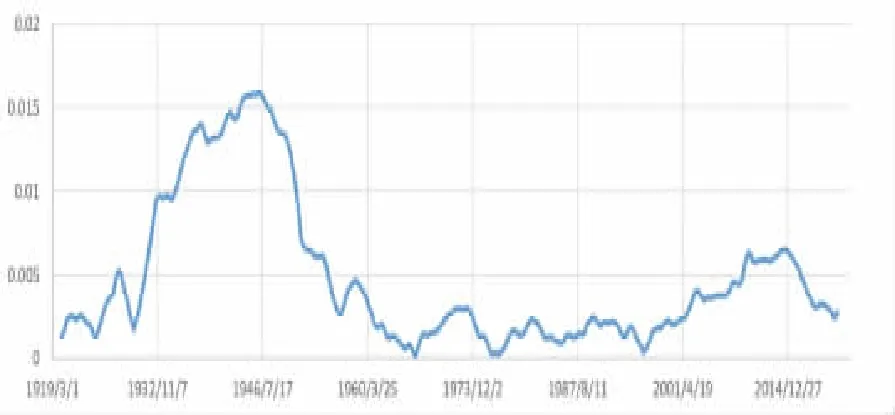
图18 Juglar周期幅度的历史演化过程

图19 Kuznets周期幅度的历史演化过程

可以看出，幅度信息序列的大小与连续性有助于判断相应的经济周期规律对资本市场影响能力的变化。三种经济周期的幅度信号在美国大萧条时期至二战后经济完全复苏前，均出现了连续衰减，并在20世纪60年代后经历了较长时间的逐渐恢复过程，证明了经济周期规律对资本市场影响能力普遍因经济危机、世界大战等因素而被削弱。同时，Kitchin周期、Juglar周期与Kuznets周期在不同历史时期的幅度值大小顺序不同，即三种经济周期规律的影响能力相当，对资本市场的长期作用都无法忽视，因此构建周期因子模型必须同时考虑三种经济周期规律的信号叠加。

四、总结

本文通过宏观经济周期理论与时间序列调和分析方法的结合，构建了经济周期多因子模型，对全球股票市场周期性波动规律进行了实证分析和建模预测。通过快速傅里叶变换（FFT），我们把经过对数同比化处理的资本市场价格时间序列从时域变换到频域进行频谱分析，并基于经典经济周期理论对应的三种周期性规律，进行高斯滤波与全球资本市场的共振信号提取，验证了三种经济周期引起的简谐波动是全球股票市场共有的普适现象。我们构建了经济周期多因子模型对全球股票市场价格波动的历史数据进行回归拟合，验证了宏观经济周期对股票市场具有显著影响并获取了拟合参数。我们通过经济周期多因子模型对股票市场未来波动趋势进行回归预测，并把样本外预测结果与真实数据进行比较，证实该模型能够实现对股票市场价格波动趋势的部分预测。

此外，本文应用周期多因子模型对美国道琼斯工业指数过去近100年的历史数据进行样本区间滚动预测分析，追溯演示了资本市场经济周期规律的历史演化过程。通过计算预期因子序列分别对三种周期因子的相位信息和幅度信息进行历史回溯，比较分析了相应的经济周期规律在不同历史时期的稳定性差异以及对资本市场的影响能力，发现Kitchin周期在过去近100年间表现出最佳的长期稳定性，其周期性规律和因子有效性几乎不受世界大战、技术革命、经济危机等重大历史事件的影响。三种经济周期规律对资本市场的长期影响能力相当，都受经济危机、世界大战等因素制约，在不同历史时期呈现差异化影响水平，共同构成了资本市场周期性价格波动的驱动力。本文的方法和结论有助于深化对资本市场价格波动机制以及宏观经济周期理论的理解，为资本市场周期性金融风险的监管防控提供参考依据和分析工具。