顾及接收机UPD的PPP分步模糊度固定方法

王 玮

1 轨道交通工程信息化国家重点实验室，西安市西影路2号，710043 2 中铁第一勘察设计院集团有限公司，西安市西影路2号，710043

近年来随着GPS和GLONASS现代化的逐步推进以及Galileo和BDS的逐步完善，提供高精度、高可靠性的实时位置服务已成为全球导航卫星系统(GNSS)精密定位的发展趋势和研究热点[1]。精密单点定位(PPP)作为一种高精度的绝对定位手段已在多个领域得到广泛应用，收敛后可在全球任意范围内提供静态cm级、动态dm级的定位精度[2]。然而，由于卫星几何构型变化缓慢以及受实际复杂环境引起的噪声影响，PPP通常需要20～30 min才能收敛到cm量级[3]。

PPP模糊度的正确固定能够显著缩短PPP收敛时间。按照PPP窄巷模糊度的恢复方式可将PPP模糊度固定方法分为两类，一类为估计窄巷硬件延迟小数部分(fractional cycle bias, FCB)方法，如Ge等[4]提出将相位未校准硬件延迟偏差(UPD)与实数模糊度进行分离，服务端通过星间单差方式消除接收机端UPD并发送给用户端，恢复模糊度的整周特性；Li等[5]提出以某一卫星或地面某一测站UPD作为基准，用户端采用非差法整网平差，同时解算出卫星端和接收机端UPD。另一类称为整数恢复钟差(integer-recovery clock, IRC)方法，如Laurichesse等[6]直接将卫星钟差与窄巷硬件延迟进行合并解算，服务端将解算的整数相位钟产品进行播发，用户端无需进行窄项UPD改正即可固定模糊度；Geng等[7]已证明FCB方法与IRC方法在数学上具有等价性，FCB方法在服务端估计时较为方便，IRC方法在用户端固定时较为便捷；Li等[2]针对部分情况下固定模糊度全集较为困难，提出部分模糊度固定策略，根据一定的准则挑选部分模糊度进行固定；Wang等[8]为解决服务端与用户端产品不统一的问题，证明3种FCB产品具有等价性，并进行实验验证；Hu等[9]对服务端多系统FCB产品质量进行分析，并在用户端采用星间单差方式进行PPP模糊度固定。

然而，目前研究主要是针对服务端FCB产品的解算及质量评估，对于用户端PPP模糊度固定的研究较少。当前用户端采用星间单差方式消除接收机端UPD的影响，基准星选取不当会对模糊度固定造成极大影响，从而使PPP模糊度无法固定。因此，本文提出一种顾及接收机UPD的PPP分步模糊度固定方法，用户端基于非差法和服务端FCB产品估计接收机端UPD，并依据PPP窄巷模糊度协方差大小进行分步模糊度固定。

1 数学模型

1.1 传统星间单差方法

对伪距和载波观测量消电离层组合，消除电离层延迟一阶项影响：

(1)

(2)

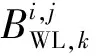
(3)

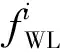
(4)

由于窄巷模糊度波长之间存在相关性且其波长较短，通常采用LAMBDA[11]算法进行模糊度搜索固定。固定后的单差模糊度作为约束条件代入滤波器，可得到PPP固定解。

1.2 顾及接收机UPD的分步模糊度固定方法

考虑到接收机端UPD，将UPD表示成虚拟观测方程：

(5)

对于用户端，利用各卫星端UPD对观测卫星的模糊度进行改正，理论上改正后的模糊度仅剩接收机端UPD，具有相近的小数部分。需要注意的是，服务端UPD产品为星间单差UPD，因此改正后的模糊度除接收机端UPD外还包括参考星UPD。将这些接收机端UPD的近似值采用与整数无关的三角函数进行计算，得到接收机端UPD的估计值：

(6)

将得到的接收机端UPD代入PPP模糊度浮点解中，扣除卫星端UPD即可得到整周模糊度估计值。由于估计的接收机端UPD包括参考星UPD，同时服务端UPD为星间单差UPD，因此PPP模糊度浮点解经卫星端UPD产品和所估计的接收机端UPD改正后，可得到整周模糊度估计值。

同理，由于消电离层模糊度不具备整数特性，将其分为宽巷、窄巷分别进行固定。非差宽巷模糊度波长较长，可直接取整固定。

(7)

式中，B为宽巷模糊度浮点解，N为其取整结果，σ为宽巷模糊度中误差。当取整成功率大于0.999 时，认为其正确固定。由固定的宽巷模糊度和消电离层模糊度可得到窄巷模糊度浮点解：

(8)

同理，窄巷模糊度浮点解经卫星端和接收机端UPD改正后，由于其波长较短且模糊度之间具有相关性，可采用分步模糊度固定方法：

2)采用LAMBDA[11]算法对非差窄巷模糊度进行降相关并搜索，若通过Ratio值检验则认为PPP模糊度固定成功，否则进入步骤3)。

3)对非差窄巷模糊度进行降维处理，即删去协方差最大的模糊度，对剩余模糊度子集进行固定，若通过Ratio值检验则输出PPP固定解。否则重复步骤2)、3)，直至PPP模糊度成功固定，或者窄巷模糊度维数小于4按照PPP浮点解输出。

2 实验与分析

选取全球225个MGEX(multi-GNSS experiment)测站作为服务端进行UPD产品的生成与发布，观测日期为2019年年积日81。另选取未参与服务端解算的14个MGEX测站作为用户端，以验证方法的有效性。测站真值坐标选取SINEX(solution independent exchange format)周解。表1为服务端UPD解算策略，采用消电离层组合消去电离层延迟一阶项影响，数据采样率为30 s，卫星截止高度角设为10°。卫星轨道和钟差均采用德国地学研究中心(German research centre for geosciences, GFZ)发布的精密产品进行改正，对流层湿延迟采用随机游走模型进行估计，接收机钟差当作白噪声进行估计。

表1 服务端UPD解算策略

服务端采用非差法进行UPD估计，由于卫星宽巷UPD较为稳定，一天估计一组，而卫星窄巷UPD波动较大，通常15 min估计一组。将生成的UPD产品播发给225个MGEX测站以检验UPD产品的精度。经UPD改正后的PPP宽巷和窄巷模糊度残差分布如图1所示，从图中可以看出，97.4%的宽巷残差和93.6%的窄巷残差分布在±0.25周之内，表明服务端生成的UPD产品具有较好的精度，可以播发给用户端使用。

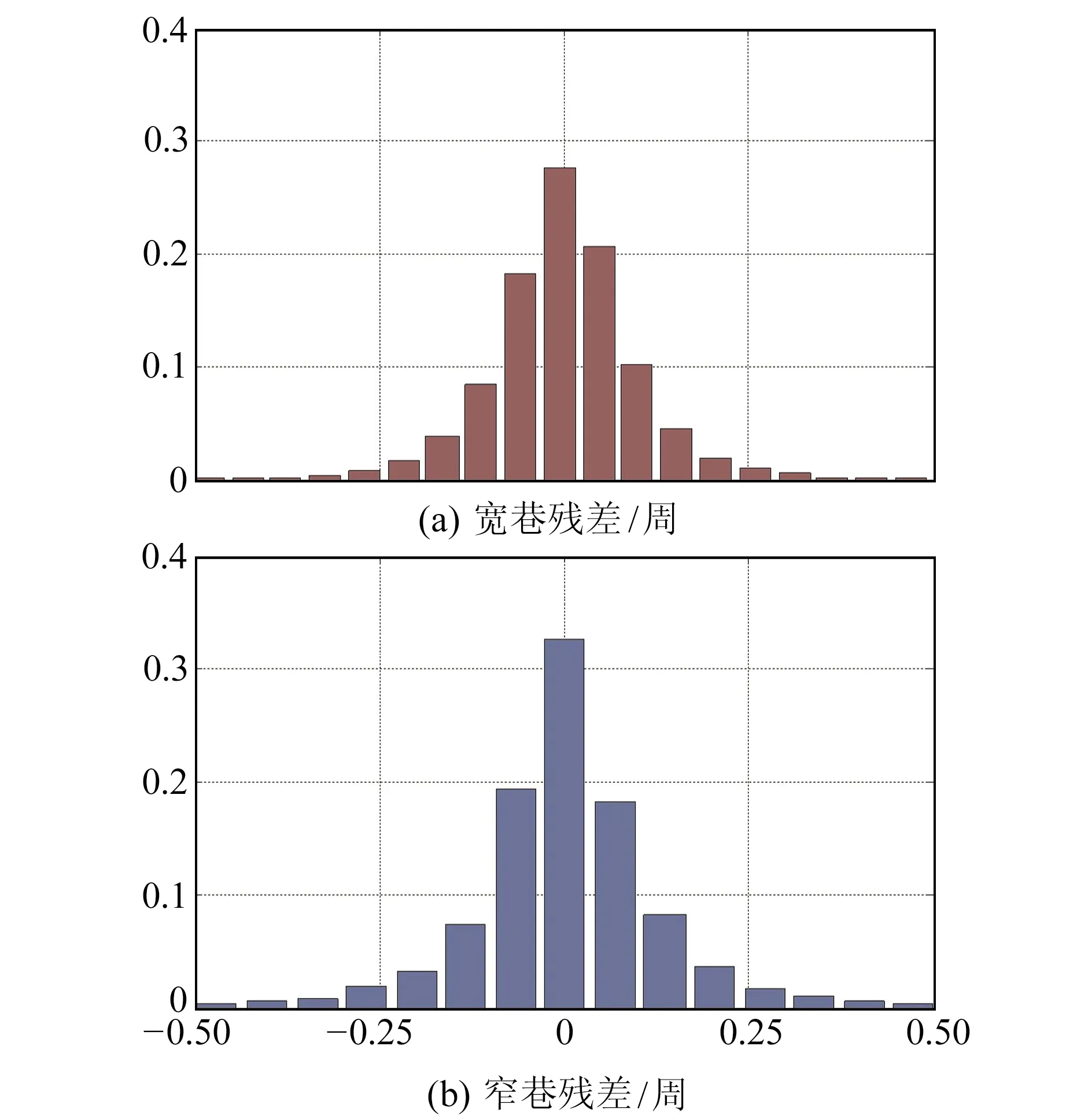
图1 经UPD产品改正后的宽巷残差和窄巷残差分布

对于全球用户端14个MGEX测站，分别采用PPP浮点解(PPP-Float)、常规PPP星间单差法固定模糊度(PPPAR-SD)和顾及接收机UPD的分步模糊度固定方法(PPPAR-UD)进行求解。图2为静态和仿动态条件下CEDU测站3种方法的解算结果，从图中可以看出，PPP模糊度的正确固定能够显著缩短PPP初始化时间，较之传统方法，新方法效果更加显著。

图2 静态和仿动态情况下3种方法的定位结果

图3为静态和仿动态条件下用户端14个MGEX测站采用3种方法在30 min的定位精度，从图中可以看出，静态情况下，PPP浮点解平均精度为7.8 cm，传统星间单差方法为2.5 cm，本文所提方法为1.8 cm。与PPP浮点解相比，静态情况下传统方法和新方法定位精度分别提升68.3%和76.4%。仿动态情况下，PPP浮点解平均精度为14.4 cm，传统星间单差方法为4.9 cm，本文所提方法为2.2 cm。与PPP浮点解相比，仿动态情况下传统方法和新方法定位精度分别提升65.7%和84.7%。从上述分析可以看出，与传统方法相比，无论静态还是仿动态情况下，本文方法都能够显著提高PPP短时间内的定位精度。

图3 静态和仿动态情况下用户端14个MGEX测站的定位精度

为分析用户端14个MGEX测站的收敛时间，收敛条件为N、E、U方向的定位偏差均小于10 cm且其后5 min均满足该条件[12]。图4为静态和仿动态情况下用户端14个MGEX测站采用3种方法的收敛时间，从图中可以看出，静态情况下，PPP浮点解平均精度为22.3 min，传统星间单差方法为9.8 min，本文所提方法为6.7 min。与PPP浮点解相比，静态情况下传统方法和新方法收敛时间分别缩短56.3%和69.9%。仿动态情况下，PPP浮点解平均精度为41.0 min，传统星间单差方法为15.7 min，本文所提方法为11.9 min。与PPP浮点解相比，仿动态情况下传统方法和新方法收敛时间分别缩短61.8%和71.1%。表2为用户端14个MGEX测站的定位精度及收敛时间，从表中可以看出，与传统方法相比，本文所提方法无论在静态还是仿动态情况下均能显著提高PPP短时间内的定位精度和缩短PPP收敛时间。

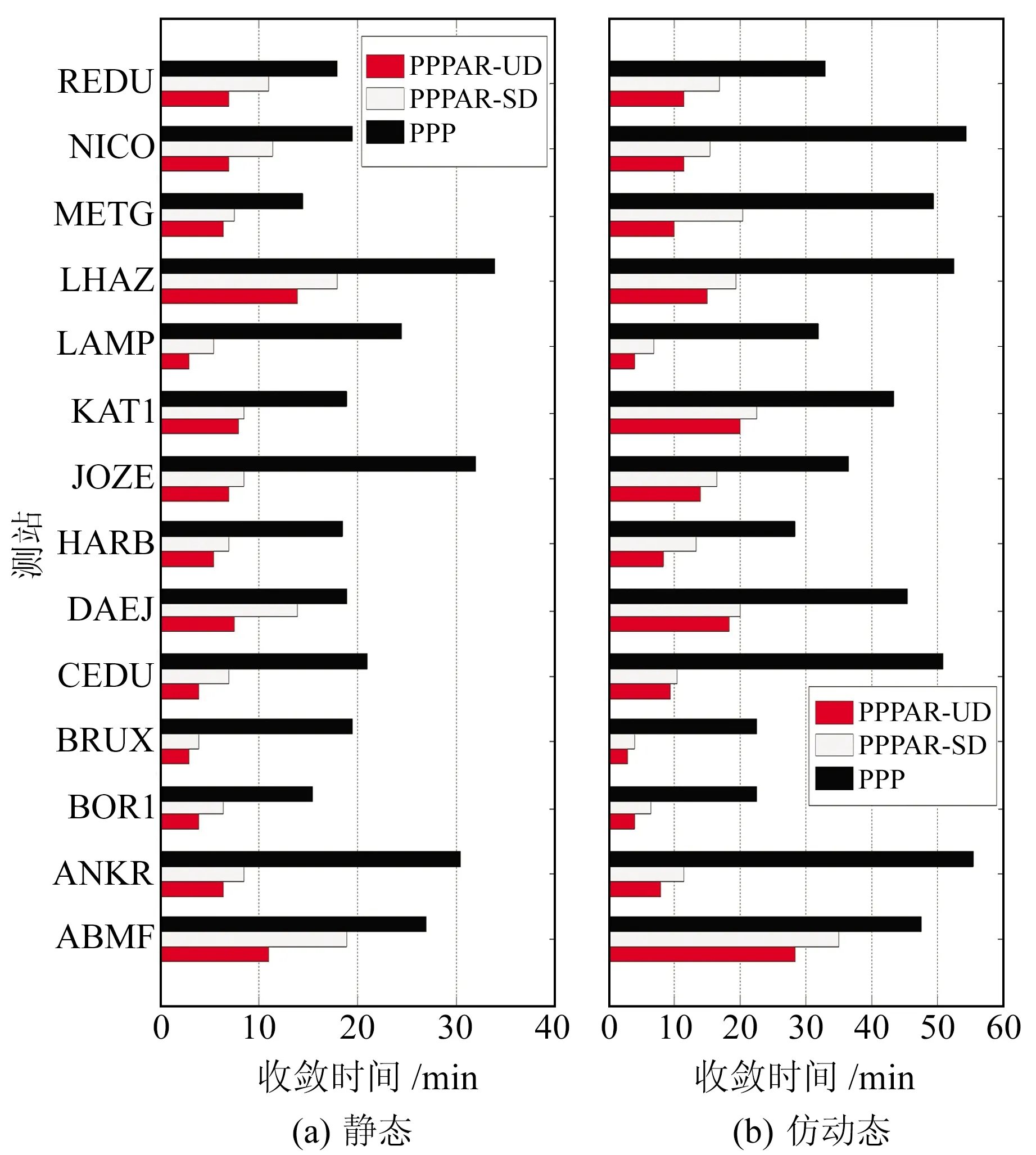
图4 静态和仿动态情况下用户端14个MGEX测站的收敛时间

表2 用户端14个MGEX测站的定位精度及收敛时间统计

3 结 语

针对用户端基准星选取不当对PPP模糊度固定造成干扰，使模糊度固定错误或无法固定的问题，本文提出顾及接收机UPD的PPP分步模糊度固定方法。基于非差法和服务端FCB产品，采用与整数无关的三角函数得到接收机端UPD估计值，依据非差窄巷模糊度协方差大小进行分步模糊度固定。选取全球225个MGEX测站作为服务端进行UPD产品的生成与发布，未参与服务端解算的14个MGEX测站作为用户端进行方法验证。实验结果表明，与PPP浮点解相比，静态情况下传统方法和新方法定位精度分别提升68.3%和76.4%；收敛时间分别缩短56.3%和69.9%。仿动态情况下传统方法和新方法定位精度分别提升65.7%和84.7%；收敛时间分别缩短61.8%和71.1%。与传统方法相比，本文所提方法无论在静态还是仿动态情况下均能显著提升PPP定位精度和缩短收敛时间。