组合式凸轮轴径向滚花装配机理及连接强度研究
张 鹏 曹泽泽 寇淑清 王 涛 郭继保 李金哲 吴 磊
1.太原理工大学机械与运载工程学院,太原,030024 2.吉林大学辊锻工艺研究所,长春,1300223.太原通泽重工有限公司,太原,030032
0 引言
组合式凸轮轴采用新型分体式设计与集成式装配理念,在制造精度、生产成本、生产效率、材料优化、轻量化、近净成形及节能减排等诸多方面具有传统铸锻凸轮轴无法企及的优势[1]。组合式凸轮轴的核心技术之一为分体部件的装配连接工艺。滚花连接工艺因具有常温局部变形小、装配精度高、自动化程度高及通用性强的特点而备受关注,并逐渐细分为轴向及径向滚花过盈连接方法[2]。
装配压装力是组合式凸轮轴滚花连接重要的过程参数,静扭强度及凸轮外廓精度则是重要的装配质量指标[3]。张弛等[4]采用模拟结合试验的方法定性地研究了影响压装或扭转工艺的因素,总结出连接区面积、分体件材料匹配程度等均对压装力、静扭强度有显著影响,然而研究未考虑各工步间残余应力的传递,且压装模型基于切削轴齿,这与实际情况差异明显。寇淑清等[5]采用有限元分析与滚花试验结合相互验证的方式,研究了关键滚花参数对轴向滚花过程中轴体表面应力、应变分布规律,轴齿成形、刀具负荷、装配过盈量的影响,但研究仅针对轴向滚花过程,且未与压装及静扭过程结合。已有研究多定性研究滚花连接强度的影响因素,缺乏对装配机理的深入分析,且关于径向滚花过盈连接的研究鲜有报道。
如何在保证静扭强度的同时减小压装力是凸轮轴装配的研究重点,而明确影响压装力和静扭强度的因素,并平衡两者的取值是首要前提。基于此,本文分别建立了滚花、压装及静力扭转的多工况子模型,并预测不同装配参数、轴管与凸轮材料的匹配对装配压装力、静扭强度及凸轮外廓变化的影响规律,明确径向滚花、压装及扭转测试过程中轴齿变形机制和装配连接机理。模拟与试验结果的对比验证了模拟结果的有效性。
1 径向滚花过盈连接原理
根据凸轮与轴管相对硬度的不同,分为轴向滚花过盈装配和径向滚花过盈装配,后者用于凸轮硬度较轴管硬度高的装配场合,实际工况中凸轮作为配气摩擦件,须具备高硬度、耐磨损、抗点蚀等优良的机械性能,其硬度通常较轴管硬度更高,因此径向滚花连接工艺的应用更加广泛。如图1a所示,径向滚花过盈连接包括滚花及压装两步,首先利用滚花刀具在轴体外表面滚挤加工垂直于轴线的三角齿形,凸起的轴齿与凸轮内孔产生过盈,在常温下将凸轮以一定的过盈量顺次压入轴体中完成装配。由于弹性变形与回弹量不同,凸轮和轴体产生过盈压配,同时轴齿与凸轮内孔形成类似花键连接的凹凸镶嵌[6]。这种复合连接可同时提供摩擦与剪切阻力,连接强度较一般过盈连接大幅提高[7],如图1b所示。
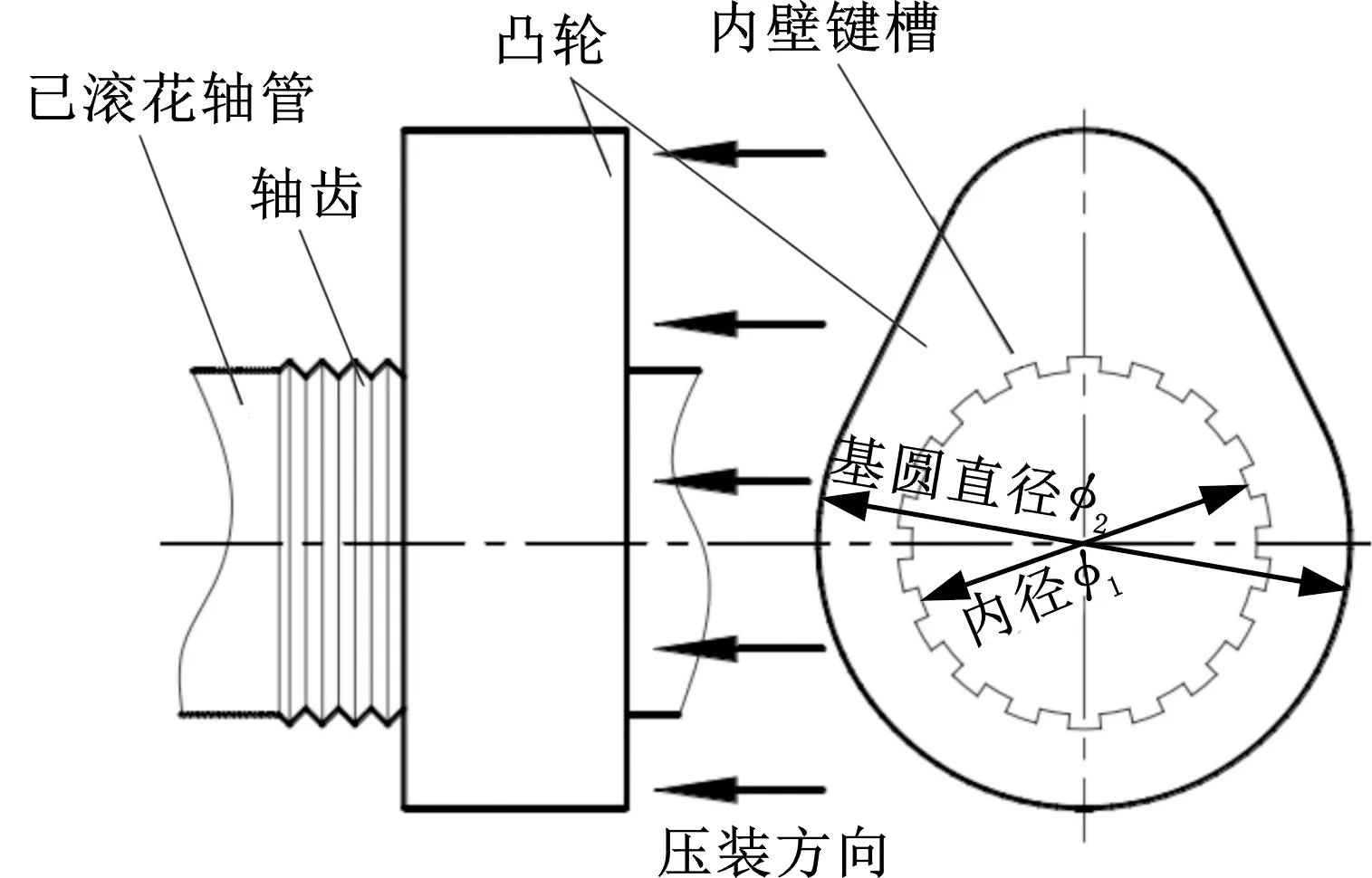
(a)径向滚花装配过程
压装时细长45钢轴管受到较大冲击力,易发生失稳弯曲现象,导致凸轮轴向精度及相位角精度降低;此外,压装时凸轮受到周向拉应力作用,导致外轮廓产生径向位移,相同条件下压装力增大,凸轮外轮廓形变越明显,增大脆性凸轮装配损伤的概率[8],因此,应尽可能减小压装力。
凸轮与轴管的连接静扭强度是组合式凸轮轴承受配气过程周期性动态载荷而不失效的重要保证,一般以超过技术要求的强度90%以上作为连接强度标准,以本文研究的某汽车凸轮轴为例,其静扭强度应不低于200 N·m[9]。
2 试验过程及子模型建立
2.1 试验过程
轴管为45钢冷拔无缝钢管,凸轮材料为GCr15钢,硬度为780HV,高于45钢硬度;轴管及凸轮的几何尺寸如表1所示。试验所用滚花刀具齿高为0.68 mm,齿顶角为80°,齿数为10。滚花试验在图2a所示的自主研制的CNC滚花装配机上实现。中空轴管通过三爪卡盘沿装配机轴向固定,并由卡盘带动可周向转动和轴向移动;两把滚花刀沿周向间隔180°均匀分布并由内凸轮机构带动完成径向进给和撤刀动作。滚花过程中,滚花刀进给压紧轴管,轴管在卡盘带动下周向旋转,借助滚刀与轴管表面的摩擦力,使滚刀也发生周向旋转,从而在轴管表面辊压区域形成一定高度的轴齿,待最终成形后,撤去滚刀完成滚花工步。如图2a所示,凸轮由位于回转圆盘上的夹具固定并可以灵活调整其相位角,压装过程中,轴管由卡盘带动,旋转的同时以2 mm/s的速度压入凸轮内孔,直至8片凸轮均与轴管完成装配。以两个凸轮为一组,将凸轮轴切割为4段扭转试样用于静扭强度测试,扭转试验台如图2b所示。

表1 轴管及凸轮尺寸参数

(a)滚花及压装试验装置 (b)扭转测试试验装置
2.2 数值模拟流程
滚花、压装与静扭强度分析是三个密不可分的连续过程。滚花刀齿参数及进给量决定了轴齿齿形以及轴齿的冷作硬化效应,是后续压装及静扭工况的重要影响因素;同样,压装后轴管与凸轮的连接特征以及冷作硬化效应,共同决定了连接静扭强度。基于此,本文制定图3所示的模拟流程图,具体如下:①建立双滚花刀对置的径向滚花子模型,模拟轴齿成形过程,分析滚花区域应力应变分布规律,撤去滚花刀,保留轴齿单元应力及应变场;②将轴管位移及应力场传递至压装工步,建立压装子模型,研究压装力变化规律,探究轴齿变形及失效过程,明确凸轮内壁应力及应变场,分析凸轮外廓位移;③将轴管及凸轮传递至静扭测试工步,加载扭矩记录静扭强度曲线,分析影响静扭强度的关键因素。

图3 径向滚花组合式凸轮轴全过程系统模拟流程图Fig.3 Overview of the simulation methodology for predicting reliability of a radial knurling assembled camshaft
2.3 数值模拟模型简化
为提高模拟效率,对模型进行合理简化:①轴体和凸轮顺次连接实现凸轮轴装配,各连接过程相同且彼此之间相互影响很小,选取单个凸轮装配过程进行模拟和分析;②基于装配试验及扭转测试观测,各过程产生的热量很少,因此,各模型均基于单一力学分析,不涉及热力耦合因素;③两把滚花刀以轴管轴线为旋转中心呈180°对置分布,刀具进给的同时在轴管的带动下自转,两刀具对轴管的作用力也呈180°轴对称分布,考虑到凸轮及轴管的几何对称性,可将其简化为1/2模型;④滚花刀材料为高强工具钢,其强度及硬度远大于轴管材料45钢的强度及硬度,因此,将滚花刀设置为刚体,不考虑其弹塑性变形;⑤采用适合于大变形分析的耦合的拉格朗日-欧拉网格(CEL)代替拉格朗日网格进行有限元分析[10]。
2.4 模型建立及边界条件设置
轴管采用CEL分析法描述,网格类型为C3D8R,凸轮由拉格朗日网格划分。将轴管固定,以滚花刀或凸轮相对轴管的运动完成各工步的动作。
各工步数值模拟三维模型如图4所示。滚花模型如图4a所示,将轴管内壁固定,对对称面施加对称约束,两把滚花刀水平对置分布,滚花刀在向轴管中心进给的同时自转;压装模型如图4b所示,对凸轮及轴管对称面施加对称约束,凸轮下表面与推板接触,侧面与圆柱型凸轮夹具接触。在压装模型基础上,将凸轮夹具撤去,并将扭转夹具加载至凸轮外表面,取消凸轮对称约束条件,通过扭转夹具对凸轮施加扭矩,实现凸轮与轴管的周向相对转动,如图4c所示。边界条件如图5所示:①限制轴管内壁径向位移(UR=0);②施加周向对称约束(UT=0)于轴管对称面;③限制轴管上下面轴向位移(UZ=0);④推板固定,凸轮上表面轴向位移为0。

(a)滚花三维简化模型 (b)压装三维简化模型

图5 扭转模拟边界条件Fig.5 Boundary conditions of torsion simulation
2.5 模拟条件及Johnson-Cook材料模型
轴管在滚花刀具及凸轮的作用下发生弹塑性变形,受到较大切向力和法向力作用,应采用基于剪切应力的摩擦模型。考虑到滚花及压装过程金属变形剧烈,轴管表面滚花处产生大量新表面,经模拟调试选择较大的摩擦因子0.28[11]。扭转过程中摩擦因子参考无润滑的过盈装配工况,经调试摩擦因子选取0.2[7]。
考虑到轴齿材料在系统模拟中所处应力状态差异较大,且会发生剧烈的塑性流动甚至剪切失效,为此采用Johnson-Cook(J-C)塑性本构准则及失效准则[12],该模型可应用于金属准静态塑性流动及失效过程。
由于各阶段发热量均很小,故忽略温度的影响,J-C强度模型[13]经简化的本构关系形式为
(1)
(2)

J-C失效模型采用损伤累积的概念来考虑随着应变率、温度及应力三轴度变化的载荷历史,材料强度或刚度受损伤的情况,当损伤度达到临界值时应力和压力设为0,损伤程度由破坏应变ε′度量,忽略温度影响,ε′可表示为[14]
(3)
σ*=p/σe
式中,D1~D4为材料失效参数;σ*为应力状态参量;p为压力;σe为等效应力。
45钢的J-C本构模型及失效模型参数见表2[14]。

表2 45钢J-C本构模型及失效模型参数
3 结果与讨论
装配试验表明,装配压装力与连接静扭强度成正相关,为实现控制装配压装力及保障连接强度的目的,揭示装配压装力和静扭强度关键影响因素成为首要问题。
3.1 滚花过程轴齿成形及残余应力
以某型号凸轮轴为典型件,使用齿高为0.68 mm、齿顶角为80°、齿数为10的滚花刀具进行实际滚花加工及同等尺寸下的数值模拟。为得到更好的云图显示效果,将轴管模拟结果在周向截取15°,轴向取1/2进行分析。图6为滚花各阶段轴管等效应变云图,塑性变形区集中于距轴管表面0.2 mm以内区域,尤其在轴管表层材料发生剧烈的塑性流动,大于1 mm深度轴管未发生任何变形,从而保持了较好圆度。如图6b所示,在轴齿中部应变最大,此处金属在三向压应力下发生剧烈变形,金属流动充分、填充性好,滚花结束前金属已完全填满滚花刀齿间隙。随着滚花时间的延长,塑性应变最大的区域出现在每个轴齿的心部,应变值增大至0.5,如图6c所示。随着轴齿顶部与滚花刀逐渐靠近,轴齿顶部材料受到更为剧烈的压应力。图6e、图6f为滚花结束后试验及模拟的轴管径向剖面图,加工齿形饱满均匀,滚花与非滚花区域过渡平滑均存在较小凸起,试验与模拟得到的轴管变形情况高度吻合。

(a)滚花1阶段 (b)滚花2阶段

(e)真实滚花齿形 (f)模拟滚花齿形
如图7所示,滚花结束后轴管表面滚花区存在明显的残余压应力,最大应力及平均应力分别为210.9 MPa和175.3 MPa。

(a)轴管等效残余应力云图 (b)径向等效应力云图
3.2 压装过程及凸轮外廓变形分析
将轴管在滚花模拟中的应变场和残余应力场传递至压装工步作为初始应变场及应力场。压装过程的Mises应力云图见图8,由于凸轮内壁存在类键槽结构,使凸轮内壁与轴管外表面的接触不连续,部分轴齿与凸轮内壁凸起处重合,从而被凸起剪切沿着进给方向平铺,挤压至轴齿间隙,形成不连续的平面与凸轮形成过盈连接,该部分的剧烈塑性变形由剪切应力引起。如图8c所示,最大应力出现在轴齿顶部,高达665 MPa,接近轴管材料的极限强度,轴齿端部可能发生断裂而产生切屑,这一现象也在装配试验中出现,被截切轴齿端部以下的部分受到凸轮内壁凸起处挤压,形成平台,另一部分与凸轮内壁凹陷处对应的轴齿嵌入内壁凹陷处,与凸轮形成类键连接。因此,过盈与键连接耦合,显著提高了轴管与凸轮的连接强度。

(a)凸轮轴齿未接触 (b)压装1阶段
模拟预测的轴齿变形与试验结果对比如图9所示。整个装配连接区在轴向呈现有规律的矩形条状分布,即前文所述不连续平面,周向为矩形齿和轴齿交替的环形分布。压装后轴管表面大部分区域压配应力大于300 MPa。图9c、图9d为试验及模拟装配连接区轴向剖面图,图中显示轴齿金属在凸轮内壁剪切力作用下向压装方向流动,并与凸轮内壁形成过盈连接。对照结果显示,模拟与试验的连接形态一致。

(a)压装试验后轴齿形态 (b)压装模拟轴齿形态
模拟和试验结果的径向剖面如图10a、图10b所示,可观察到轴齿与凸轮内孔压配应力呈圆形虚线状间隔分布,应力较大处为过盈连接区,无压配应力处为材料互嵌区,装配实物的连接区也呈现圆状虚线的连接效果,模拟与试验结果高度吻合。装配结束后,轴管与凸轮接触区域的高残余压应力有利于提高轴齿抗疲劳性能,可在轴齿承受周期性载荷时抑制微裂纹萌生。

(a)模拟结果 (b)试验结果
模拟及试验压装力如图11所示,可以看出,两条曲线均呈锯齿状上升趋势,且峰谷处对应的位移及载荷值基本相同,不同之处在于试验结果稍大,且曲线峰值波动较大。装配开始,凸轮首先与第一个轴齿接触,压装力随凸轮移动逐渐升高至6 kN,当第一个齿被凸轮内壁推平后(图8a),压装力随即降至1.5 kN,该力主要是凸轮内壁与轴齿的接触摩擦力。从图11中可以观察到,峰值载荷随凸轮压装行程增大逐渐增大,这是由于压装进程中各轴齿依次发生第一圈轴齿的变形过程,使得凸轮与轴管的接触区域和摩擦力逐渐增大。比较模拟与试验压装曲线波峰及波谷值,除第一个轴齿压装对应的峰值外,最大误差不超过9%,试验得到的最大压装力为20.5 kN,模拟值为18.7 kN,因此,模拟结果较好地预测了压装试验结果。误差主要来源于数值模拟对模型和边界条件的简化和设置的假设条件。如图11所示,模拟压装力曲线相比试验曲线,在位移上发生了偏移,这是由于凸轮内壁与轴管接触的凸起仅建立了3层单元,否则单元过于细小会导致计算成本显著升高,但较少的单元层导致该处变形较压装的实际情况小,因此对应的压装力曲线发生了位移负方向偏移。此外,实际压装过程中,轴管与凸轮无法做到理想同轴,从而压装偏移而导致压装力一定程度的增大。

图11 模拟及试验压装力曲线Fig.11 Simulation and test of axial cross-section of the joint
凸轮轴标准规定,凸轮基圆外廓误差不超过0.3 mm,ABAQUS中U1代表凸轮的径向位移,是衡量装配精度的重要参数。压装后凸轮的径向位移云图见图12,凸轮外廓的最大径向位移出现在凸轮刚度最小即最薄处,其值为0.0425 mm,大部分区域位移在0.0268~0.0346 mm之间,无需后续精磨即可满足技术要求,说明径向滚花过盈连接工艺可保持较高的凸轮外廓精度。

图12 压装过程凸轮片径向位移云图Fig.12 Radial displacement contour of the cam lobe after the press-fit process
3.3 扭转强度预测及校验
在装配后的凸轮轴上截取扭转分析试样,如图13所示,采用QD-B1静扭试验台进行破坏性扭转试验,规定扭转曲线最大值为该凸轮轴静扭强度。图13所示为试验及模拟输出的静扭强度曲线,曲线明显分为三个阶段:线性上升(轴齿弹性变形)、非线性上升(轴齿塑性变形)以及下降阶段(轴齿失效)。模拟与试验最大扭矩分别为427.2 N·m和392.3 N·m,相差6.8%,两者均高于某乘用车凸轮轴静力扭转强度(200 N·m)要求的90%。最大值对应扭转角度分别为1.15°和1.26°,模拟与试验偏差是由有限元模型的理想化及数值化误差引起,实际扭转过程中测试设备与夹具间存在机械间隙也是试验值转角过大的原因。

图13 连接静扭强度模拟与实测图Fig.13 Simulation and measurement of static torsion strength of connection
残余应力对轴齿材料的加工硬化和应变硬化有显著影响。在相同的轴齿参数下,比较滚花加工硬化对压装力及静扭强度的影响,建立齿高为0.68 mm,齿顶角为80°的轴齿模型,与前述滚花加工后传递的轴齿不同,该模型只具备轴齿的几何形状,而无法保留滚花后轴齿表面的残余应力。在齿参数一样的前提下,将直接建立的轴齿模型A(应变硬化轴齿)与传递轴齿模型B(非应变硬化轴齿)分别进行压装和扭转模拟,两者的压装及扭转模型对比结果如图14、图15所示,A模型对应材料有更高的屈服强度,使得压装力和扭转强度也较高,分别较B模型的模拟结果高11.8%和10.7%,这说明模拟中考虑加工硬化及应变硬化对准确预测压装力及静扭强度值有显著影响,本文进行系统的径向滚花-压装-扭转过程分析一体化模拟具有实际意义。

图14 应变硬化效应对压装力模拟结果的影响Fig.14 Effects of strain hardening material model on the press-fit load

图15 应变硬化效应对静扭强度模拟结果的影响Fig.15 Effects of strain hardening material model on the static torsional strength
在连接区面积不超过一定量的前提下,表3给出了不同的滚花刀几何参数及进给百分比所对应的装配压装力和静扭强度值。通过对比可知,试验与模拟压装力相差在11%以内,静扭强度值相差在10%以内,据此,判定压装力、静扭强度模拟结果真实可信,该有限元模型在一定程度上可代替试验获取装配压装力及静扭强度。
从表3中数据可以看出,压装力越大静扭强度越大,压装力最高达24.8 kN,对应齿高及齿顶角分别为0.68 mm和55°;最大静扭强度为468.2 N·m,超过乘用车发动机凸轮轴技术要求90%以上,但装配参数不同,强度值差异很大。对于单个轴齿而言,齿高越高所需压装力越大,连接强度越大,同时,随着齿顶角增大,装配压装力及连接强度也显著提高。然而,当凸轮与轴管尺寸一定时,尤其是凸轮厚度确定后,两者的连接区面积即可确定,齿数会随着单齿高度和齿顶角的增大而减少,所以当连接区面积一定时,压装力及静扭强度并非与齿高、齿顶角成正比。进给量在80%~90%之间,装配压装力和连接静扭强度均随进给量增大而增大,但超过90%后,进给量过大,会造成轴齿损坏。此外,在凸轮与轴管连接静扭强度满足技术要求后,减小压装力为主要目标,但两者成正比关系,因此需要平衡两者的取值。表3中1号参数组合在提高凸轮轴性能和降低潜在的凸轮片损伤风险方面优于其他参数组合。本文提到的模型方法对滚花刀参数优化设计和预测接头连接性能意义显著。

表3 模拟与试验的对应压装力和静扭强度
4 结论
通过建立滚花、压装和扭转测试连续工步子模型,并进行基于应力和应变场连续传递的系统模拟,结合试验验证,定量分析了刀具齿高、齿顶角和进给量三个重要参数对组合式凸轮轴径向滚花连接的影响。结论如下:
(1)滚花后轴齿表面存在227 MPa的平均残余应力,压装后凸轮与轴管大部分连接区域压配应力超过300 MPa,残余应力对压装及静力扭转结果有显著影响,进行滚花、装配及扭转的系统性模拟十分必要。
(2)滚花时仅轴管表面金属发生剧烈塑性流动,内部则无任何变形,压装力曲线呈现波动上升趋势。当齿高为0.68 mm,齿顶角为80°时可获得压装力较小,静扭强度较大的装配结果,对应最大压装力为18.5 kN,可以预见凸轮承受较大的径向扩径载荷,且轴管存在失稳风险;通过模拟预测的凸轮片外廓径向位移为0.0268~0.0346 mm,凸轮装配精度较高。
(3)模拟预测和试验静扭强度曲线的最大值分别为438.2 N·m和406.5 N·m,均超过乘用车静扭强度要求的90%以上;静扭曲线分为线性、非线性上升及下降阶段,曲线随装配参数的变化波动显著,静扭强度与压装力成正相关。
(4)装配区域一定,装配压装力、静扭强度及凸轮外廓径向位移均与滚花刀齿高、齿顶角及进给量成非线性相关。开展相同条件下模拟及试验对比,结果显示:轴齿成形及变形情况高度一致,多组对比显示压装力及静扭强度曲线吻合度高,误差均低于11%,说明模拟结果真实可信。

