六自由度平台动力学前馈柔顺控制研究
倪 涛 徐海远 李 东 张红彦
1.燕山大学车辆与能源学院,秦皇岛,0660042.吉林大学机械与航空航天工程学院,长春,130022
0 引言
现有的装配机器人大多是串联关节机器人[1-2],但串联机器人承载能力小,一般只能应用于小型、轻型零件的装配[3-4]。与传统的串联机器人相比,Stewart平台具有刚度大、负载能力强、精度高等优点[5-6],在大型部件的装配和航天对接领域应用越来越广泛[7]。在装配过程中机器人的末端执行器会与环境接触,机器人的运动会受到空间的限制[8-9],因此,需要在控制机器人位置的同时还要考虑对机器人与环境接触时相互作用力的控制[10-12]。
柔顺性是指机器人在与环境接触时能够对外部作用力产生自然顺从的能力。针对机器人的柔顺控制,CHEAH等[13]设计了一种力/位置混合控制方法,该方法将机器人末端受到的约束力和位置分开控制,进行力控制的关节不再参与位置的控制,同时参与位置控制的关节也不再参与力的控制,从而实现同时控制机器人末端位置和接触力的目的。SONG等[14]提出了一种工业机器人智能控制方法,它可以跟踪磨削工艺中工件的形状以及接触力不连续变化,根据测量数据精确控制机器人的磨削运动。KRONANDER等[15]综合考虑阻抗控制过程中,刚度、阻尼以及阻尼的时间倒数等阻抗参数对机器人控制系统稳定性的影响,提出一种刚度系数和阻尼系数可变的阻抗控制方法,仿真结果表明,该方法增加了系统的灵活性。以上柔顺控制方法需要将力/扭矩传感器安装在机械手的末端执行器、关节或底座上,通过传感器感知机器人受到的力,将力偏差作为系统的输入量,调整机器人的位姿。然而,精密的传感器价格昂贵, 此外,在机器人关节处安装力传感器会使关节刚度减小,限制机械手的有效载荷能力和操作环境。
由于使用传感器检测外力具有一定的局限性,相关学者提出了无传感器柔顺控制方法。LEE等[16]通过监测电机电流来估计碰撞引起的外部力矩,提出了一种不需要任何传感器的碰撞检测方法。DUTTA等[17]提出了一种应用在六自由度R-S-S(旋转-球形-球形)结构的并联机械手上的无传感器主动柔顺控制方法,该方法仅基于执行器电流反馈估计关节扭矩,设计了一种三层级联阻抗控制器,大大节省了成本。
考虑到在机器人末端安装传感器会使机器人的承载能力减小,机器人的制造成本也会大大增加,因此为了解决这个问题,本文在不使用任何外力/力矩传感器的情况下,提出一种基于摩擦补偿的六自由度平台柔顺控制方法。采集伺服电机编码器的数据,利用库仑摩擦模型和黏性摩擦模型对伺服电动缸的摩擦力进行估算,并通过实验确定各电动缸的摩擦参数。最后提出了一种动力学前馈控制方法,实验结果表明该方法在六自由度平台柔顺控制中有效且可靠。
1 理论模型建立
1.1 运动学模型
本文所研究的Stewart并联六自由度平台是一种6-UPS结构。平台电动缸与动平台通过球铰连接,与固定平台通过万向节连接。点ai和bi(i=1,2,…,6)表示球形接头和万向节的中心。
固定坐标系Bxyz和移动坐标系Px′y′z′如图1所示,x轴是b1b2的中垂线,z轴垂直于固定基座的平面,y轴由右手定则确定。x′轴是a1a2的中垂线,z′轴向上并垂直于移动平台的平面,y′轴由右手定则确定。
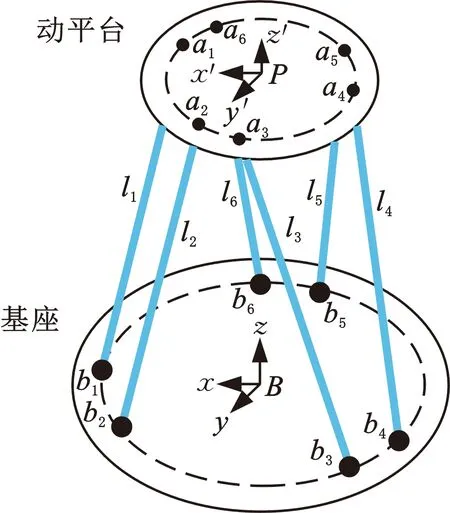
图1 Stewart平台结构图Fig.1 Structure diagram of Stewart platform
定义广义坐标向量q=(x,y,z,φ,θ,φ)T,其中,(x,y,z)表示移动坐标系{P}相对于固定坐标系{B}的位置,(φ,θ,φ)表示移动坐标系{P}相对于固定坐标系{B}的空间姿态[18]。
为了避免奇异位置在平台正常工作的情况下出现,可以采用Z—X—Z欧拉角的坐标变换顺序,即移动坐标系Px′y′z′相对于固定坐标系Bxyz的姿态可以通过绕z′轴旋转φ角度,然后绕x′轴旋转θ角度,最后绕z′轴旋转φ角度得到。移动坐标系{P}相对于固定坐标系{B}的旋转矩阵可以表示为
BRP=

(1)
式中,c表示cos函数,s表示sin函数。
(2)
(3)

(4)
(5)


图2 坐标系分配[20]Fig.2 Coordinate system assignment[20]
1.2 动力学模型
选择拉格朗日方程作为Stewart平台的动力学方程[21-23]:
(6)
τ=(fx,fy,fz,τφ,τθ,τφ)T
(7)
(8)
(9)

设Fd=(f1,f2,…,f6)T表示电动缸伸缩杆的驱动力矢量,则τ和Fd之间转换关系为
τ=(J-1)TFd
(10)
式(6)表示末端姿态的广义向量q的动力学方程,把它转换到关节空间中,有
(11)
Ml(l)=JTM(q)J
(12)
(13)
Gl(l)=JTG(q)
(14)
2 基于摩擦补偿的动力学前馈控制
2.1 摩擦模型
Stewart平台的摩擦包括电机的摩擦和滚珠丝杠与螺母接触面相对运动的摩擦。在研究电动缸运动的摩擦力时,可以把这两部分摩擦力作为一个整体来研究。动态摩擦模型虽然能较准确地描述摩擦特性,但它具有摩擦参数多、辨识困难等特点,不适合实际应用。表达摩擦的经典模型之一是库仑摩擦模型,并且库仑摩擦模型进一步发展为由库仑摩擦、黏性摩擦和Striebeck摩擦组成的静摩擦模型[24]。本文采用图3中的库仑和黏性摩擦模型,该模型简化了低速的非线性区域,对高速区域使用黏性摩擦模型可以更准确地描述摩擦力与速度的线性关系[25]。
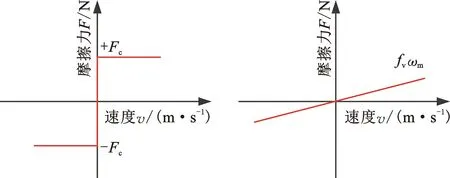
(a)库仑摩擦 (b)黏性摩擦
库仑摩擦和黏性摩擦数学模型用公式表示为
(15)
(16)
式中,Ff为总摩擦力;Fc为库仑摩擦力;fv为黏性摩擦系数;v为滚珠丝杠与螺母之间的相对速度;P为滚珠丝杠的导程;ωm为电机的角速度,由于没有减速机,滚珠丝杠的角速度等于电机的角速度。
温淑焕[26]将电机的转动惯量和滚珠丝杠的转动惯量合并,建立了滚珠丝杠在运动过程中考虑摩擦的运动学模型:
(17)
式中,Td为电磁转矩;Jm、JL分别为电机的转动惯量和滚珠丝杠的转动惯量;Tvf、Tcf、TL分别为伺服运动系统的黏性摩擦力矩、库仑摩擦力矩和滚珠丝杠的负载力矩。
系统的受力力矩T与受力F之间关系如下:
(18)
式中,η为滚珠丝杠的传动效率。
2.2 动力学前馈控制
柔顺控制主要用于机器人与环境相互作用的工作场合,可以减少机器人与环境之间的接触力,保证机器人工作过程的安全性和可靠性[27]。在实际应用中,柔顺运动平台的速度较小,一般可以忽略科氏力和离心力的影响,此时只要补偿了平台自身的重力和摩擦力,平台就可以跟随外力进行柔顺运动。

Fd=Gl(l)=JTG(q)
(19)
在力矩模式下,可以通过伺服电机的编码器获得电机的转角。将电机转角代入正运动学公式,得到Stewart平台的末端位姿,然后将平台末端的位姿信息代入逆动力学,得到6个电动缸的驱动力Fd,最后计算出电机的重力项力矩TG。TG和Fd之间的关系可通过式(18)得到。动力学前馈控制器的总体框图见图4,其中,Te为PID控制器根据位置偏差计算的力矩值。

图4 动力学前馈控制框图Fig.4 Control framework for dynamic feedforward

(20)
当平台向下运动时,电机的驱动力矩Tm为
(21)
式中,Kp、Ki、Kd分别是比例系数、积分系数和微分系数;e(k)为期望的电动缸的长度与当前实际电动缸的长度的差值。
本文提出的柔顺控制方法利用PID控制律对关节的位置进行控制,实现对末端位姿的精确跟踪,此外由于采用了PID控制方法,可以使平台在力消除后回到初始姿态。式(4)用于计算6个电动缸的速度,当受到外力作用时,平台的位置会发生微小的变化,动力学模型和摩擦模型描述了该位置的转矩,反馈作用于电机。平台受到外力时会顺应外力移动。
3 实验
为了验证所提出的Stewart平台动态前馈控制算法,搭建了实验平台系统,实验系统示意见图5。

图5 实验系统示意图Fig.5 Schematic of experimental system
实验系统采用Stewart平台作为驱动机构。驱动电动缸的电机为INVT的SV-ML08-0R7G-2-1A0-100X,额定转速为3000 r/min,采用CANET-8E-U通信板进行数据传输,满足同步性和实时性的要求。最后,采用ISV-DA200伺服驱动作为实时控制系统,实现更精确的定位和与CAN板的连接。系统的性能指标如表1所示。
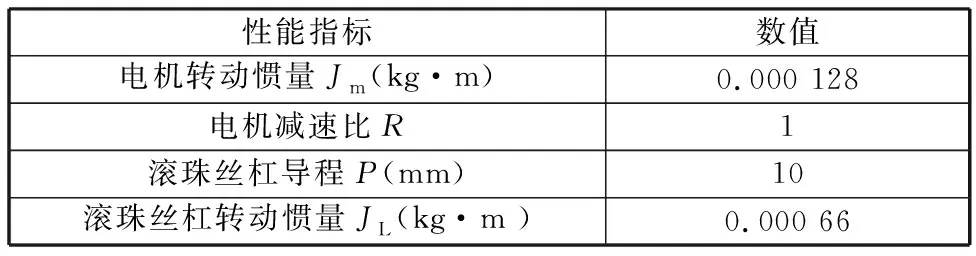
表1 Stewart平台性能指标
实验一是对摩擦参数进行辨识,采用离线参数辨识方法。以电动缸1为例,将无外部负载的电动缸拆下并水平放置。在位置控制模式下,从低到高等间隔发出速度指令(-10~10 rad/s),然后在系统稳定运行时通过编码器反馈值读取电磁转矩,此时获得的电磁转矩近似等于摩擦转矩。当电机工作时电磁转矩不是一个固定的数字,因此,当电动机以一定速度运动时,有必要收集尽可能多的数据,并找出这些数据的平均值作为该速度下的电磁转矩。电动缸实际测量的摩擦力矩离散数据如图6所示。用最小二乘法对测量的离散数据进行线性拟合,可以求得直线的斜率和截距。直线的斜率表示黏性摩擦系数,截距表示库仑摩擦力矩。参数辨识结果如表2所示。

图6 离线摩擦参数辨识Fig.6 Off-line friction identification
第二个实验在力矩模式下进行,分析电机转矩误差。给定沿z轴的正弦位置信号输入,分别采集6台电机的力矩反馈数据。从收集的数据中减去重力产生的力矩和摩擦力矩,结果如图7所示。结果表明,1、3、6缸电机力矩控制偏差均值为0.1 N·m,2、4、5缸电机力矩控制偏差均值为0.2 N·m,电机力矩误差值主要与摩擦转矩识别的精度有关,其次与动力学参数的准确性和电动缸的机械变形有关。

(a)电动缸1力矩补偿曲线 (b)电动缸2力矩补偿曲线 (c)电动缸3力矩补偿曲线
动力学前馈控制对六自由度平台的摩擦项和重力项进行了补偿,平台受到外力时会沿着力的方向移动。一旦外力被移除,动力学前馈控制将产生收缩轨迹,使Stewart平台返回到受力前的初始位姿。为了验证这种柔顺运动,进行了以下实验。图8显示了x轴方向的水平力作用在上部平台上时,在动力学前馈控制过程中电动缸1、3、5的实际扭矩。该图可分为三个阶段:①力矩控制模式的静态状态,发送给电机的转矩消除了Stewart平台的重力和摩擦力,反馈力矩约为零;②柔顺阶段,对末端执行器施加外力时,末端执行器将沿所施加力的方向顺应地移动;③恢复阶段,当力被撤去时,Stewart平台会恢复到原始状态。

图8 柔顺控制期间的电动缸1,3,5力矩Fig.8 Joint 1,3,5 torques during compliant control
根据图1所示的Stewart平台结构,当动平台向x轴方向移动时,电动缸1收缩,电机的力矩为正,电动缸3、5伸长,电机的力矩为负。
使用图5所示的实验装置,通过在Stewart平台上施加外力来验证柔顺运动的准确性。在上平台施加沿x轴方向的水平外力,实验的完整步骤如图9a所示。收集每个电动缸的伸长量,通过运动学计算上平台中心点的坐标。由图9b可以明显看出,上平台中心点的位置沿力的方向移动,当力被移除时,它会返回到原来的位置,验证了所提方法的正确性。施加沿x轴方向的水平外力,则沿x轴方向的偏移最大,y轴方向的跟踪误差在0.01~0.02 m范围内,z轴方向的跟踪误差在0.005~0.01 m范围内。

(a)柔顺控制操作连续步骤照片
4 结论
本文提出了一种基于摩擦补偿的Stewart平台柔顺控制策略。首先在离线状态下,利用库仑摩擦模型和黏性摩擦模型估计出各个电动缸的摩擦力,然后在整体动力学模型中补偿平台的重力和摩擦力,提出了一种动力学前馈控制方法,使机器人在不使用任何力传感器的情况下就能够在外力作用下柔顺地运动。通过实验测量出了电动缸的摩擦模型,并验证了柔顺控制的有效性。串联机器人一般不适用于大型工件的装配,而在并联机器人上安装高精度传感器成本较高,所提出的动力学前馈柔顺控制方法可以发挥重要作用,减少运动过程中突然的刚性碰撞所造成的危害。后续将考虑如何提高摩擦估算模型的精度,以提高平台的稳定性。此外,还要对实际装配过程中受力情况进行深入研究,达到柔顺装配。

