“一次多练”不如“一题多变”——以平行四边形面积计算的一道习题为例

□ 章宏俊

许多教师在布置作业时，都是先让学生做书本的习题，再做配套的习题，若有时间，就在此基础上再编拟一定数量的习题继续让学生练习。这种现象被称为“一次多练”。有人认为，只要有一定数量的练习，量变就会产生质变，肯定能够促使学生掌握所学内容。愿望是美好的，结果却不一定尽如人意。练习的目的是帮助学生巩固知识、形成技能、发展思维。要达成这一目的，确实需要进行一定数量的练习。然而这种“只重数量不重质量”的做法不利于减轻学生的作业负担；割裂了题目之间的联系，不利于学生的理解；学生不清楚题目的变化发展，不利于思维的发展。因此，练习的功能也就难以很好的实现。

“一题多变”指的是从一道题目变化出各种题目，让学生在一系列变化练习中，明白题目的来龙去脉、变化发展，既巩固知识，又发展思维和解题能力，还能够促进学生知识系统化，是一种比较好的练习形式。那么，如何进行既突出联系又体现层次和发展的“一题多变”呢？下面以平行四边形面积计算的一道习题为例，与读者分享“一题多变”的一次经历。

以人教版教材五年级上册“练习十九”第2 题的第3 小题为例（如图1），教师可以通过六个层次的变化练习挖掘该题的教学资源。

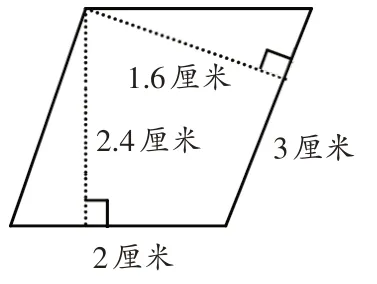
图1

层次一：独立练习，培养观察分析能力

本题有两组底和高，任意一组底与高相乘就能求出这个平行四边形的面积，即2×2.4＝3×1.6＝4.8（平方厘米）。求平行四边形面积时，只要找出任意一组相对应的底和高的数据，就可以计算出面积，没有必要把两组底和高的数据全都找出来。

这样做，要求学生仔细审题，找出所需要的数据，从而培养学生的观察分析能力。

层次二：改编数据，培养灵活解题能力

改编题目，少画一条高（如图2），求出这个平行四边形的面积。高5 厘米相对应的底没有标明数据，要求学生观察找出高5 厘米相对应的底是4厘米，而不是6 厘米，不能胡乱搭配。这样做的目的是进一步巩固平行四边形面积计算的知识，找准相对应的底和高。同时培养学生仔细观察、灵活运用知识的能力。

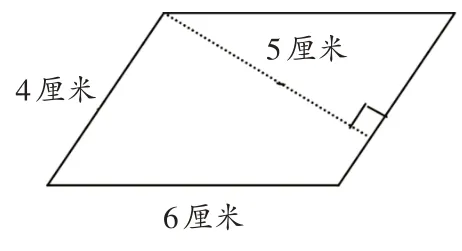
图2

层次三：利用等式求高，培养逆向思维能力

平行四边形有两组底和高，知道两条底的长度和一条高的长度，如何求出另一条底上高的长度？先画出另一条底上的高，标上h（如图3），再写出等式：6h=4×5，根据这个等式就能求出另一条高h的长度（厘米）。这样就改编成了逆向思考的题目，知道面积和底（高），如何求高（底），练一练（如图4和图5）。

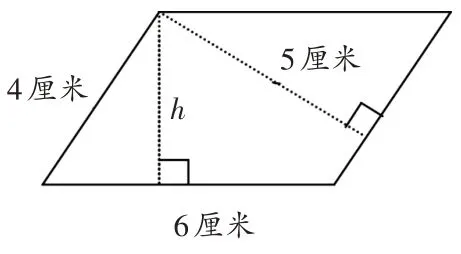
图3

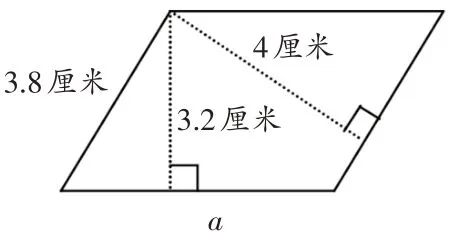
图4

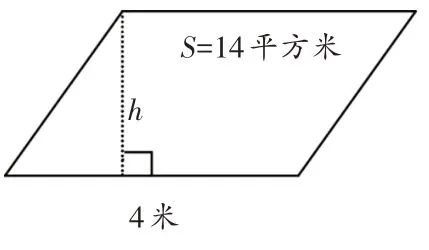
图5

根据题意进行改编，引出逆向思考题目，既加强了题目之间的联系，又培养了学生的逆向思维能力，及时进行练习还有利于巩固知识。

层次四：直接文字呈现，培养学生的综合运用能力

再进行变化，不出示图形，文字呈现题目：一个平行四边形，相邻两条边分别是6厘米和4厘米，其中一条底上的高是5 厘米，求这个平行四边形的面积。

没有了图形，这条5厘米的高应该与哪一条底相对应呢？这就涉及三角形三边关系的知识，学生自己通过画图进行分析，得出结论：高5 厘米不可能画在底6厘米上面，因为直角三角形斜边的长度一定大于任何一条直角边的长度，而直角三角形斜边为4厘米，直角边不可能是5厘米，所以高5厘米应该画在4厘米的底上。

这样做，从直观到抽象，要求学生综合运用知识，进行合理分析、严密推理，提高了学生的分析能力，促进学生深度学习。

层次五：多元变换，培养比较辨析能力

继续变题引发学生思考：如果相邻两条边4厘米和6 厘米不变，高是多少厘米才能画在4 厘米的底上？（大于4厘米，小于6厘米）如果相邻两条边4厘米和6厘米不变，高是多少厘米可以画在任意一条底上？（小于4厘米）

如果做一个课件，通过拉一拉动态展示高的变化过程（图形略），那么效果会更好。在举例概括的过程中，既巩固了平行四边形“高”的知识，又清晰了三角形三边关系，培养了学生的辨析能力。

层次六：自主编题，培养感悟能力

根据刚才变化的题目要求学生自己编拟一题，通过编题可以考查学生的感悟能力。如学生编拟的题目：（1）求这个平行四边形的周长（如图6）；（2）求阴影三角形的面积（如图7）。

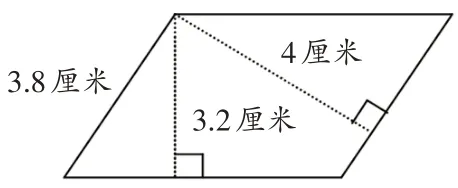
图6

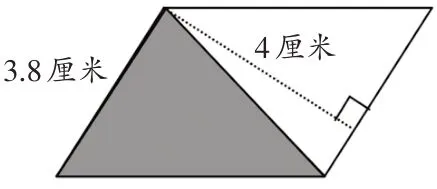
图7

这两位学生都编拟出既与原题目有紧密联系又有一定思维难度的题目，可以供其他学生进行参考，发展了学生的思维。让学生当老师是最好的学习方式之一。学生在互相编题、解题的过程中，加深了对知识的理解，促进了感悟能力的提高。

如果把学生编拟的题目加上教师编拟的一些题目，编成练习（涉及以上五种变化），进行课内检测（题目略），就可以帮助学生当堂巩固知识。高效的课堂应努力提高课堂教学效率、追求课内落实教学目标。因此，一题多变后及时进行检测，便于教师发现问题、对症下药、及时弥补，学生在发散思维的过程中，深入理解、及时内化知识，从而有效提高课堂教学的质量。

一题多变，以一题编出多题，帮助学生拓宽思路，构建知识网络，形成知识体系。学生在编题过程中构建系统，在系统练习中感悟，在感悟中提升。